Cel üwiczenia

Poznanie podstawowych wielkoĞci fotometrycznych, ich wizualnych i fizycznych metod pomiaru oraz

zapoznanie siĊ z zasadami działania fotometru Lummera-Bredhuna oraz fotoogniwa poprzez wyznaczenie
natĊĪenia Ĩródła Ğwiatła metodą wizualną i fizyczną, a takĪe wykreĞlenie wykresów i=f(E), E=f(Į) oraz badanie
przepuszczalnoĞci filtrów szarych przy zastosowaniu metody fizycznej.

CZ. I Pomiary fotometryczne z wykorzystaniem fotoogniwa selenowego

Układ i metody pomiarowe

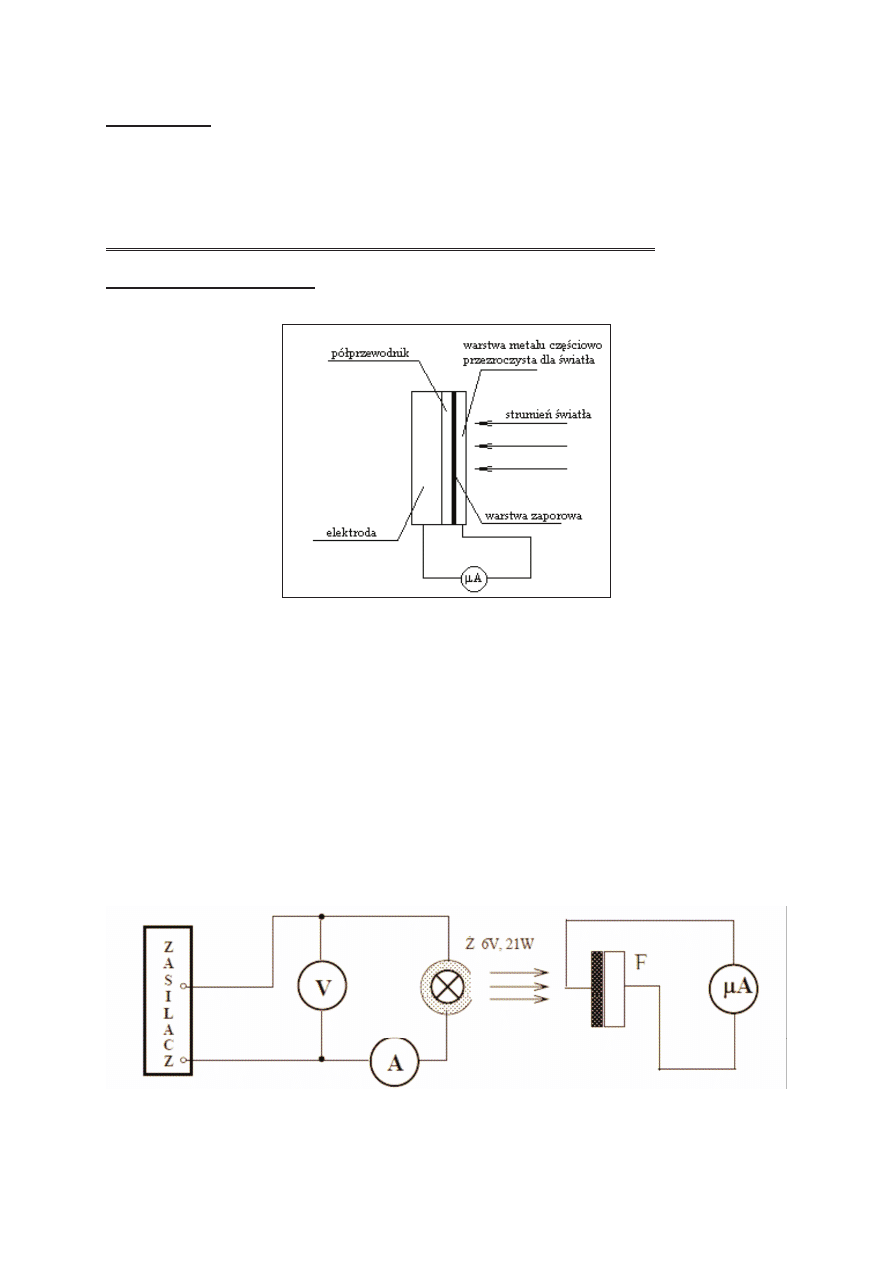
Podczas wykonywania üwiczenia korzystaliĞmy z fotoogniwa selenowego, którego schemat jest

zaprezentowany poniĪej.

Rys. 1. Schemat budowy fotoogniwa

Zasada działania fotoogniwa jest oparta na właĞciwoĞciach złącza metal-półprzewodnik. Absorpcja

Ğwiatła w obszarze ładunku przestrzennego złącza metal-półprzewodnik powoduje wybijanie elektronów z
atomów i powstawanie par elektron-dziura, które są natychmiast rozseparowywane przez pole elektryczne
wystĊpujące w tym obszarze. W obwodzie dołączonym do biegunów fotoogniwa powstaje prąd elektryczny i o
niewielkim natĊĪeniu, mierzony mikroamperomierzem.

Pierwszym zdaniem było mierzenie natĊĪenia prądu płynącego w obwodzie w zaleĪnoĞci od odległoĞci

Ĩródła Ğwiatła i wyznaczenie charakterystyki i=f(E). W tym celu odsuwaliĞmy fotoogniwo od Ĩródła Ğwiatła co 5
cm począwszy od odległoĞci 30 cm a koĔcząc na 95 cm.

Drugim zadaniem było mierzenie natĊĪenia prądu płynącego w obwodzie w zaleĪnoĞci od kąta padania

Ğwiatła na fotoogniwo. Na odległoĞci fotoogniwa od Ĩródła równej 30 cm wychylaliĞmy fotoogniwo o kąt od 0°
(płytka fotoogniwa jest prostopadle do Ĩródła Ğwiata) do 70° co 10° w obie strony. Dla wychylenia fotoogniwa w
lewo przyjĊto notacjĊ z „-”.

Kolejnym zadaniem było zbadanie przepuszczalnoĞci filtrów szarych. W tym celu mierzyliĞmy

natĊĪenie prądu fotoelektrycznego i dla Ğwiatła przepuszczanego przez filtry.

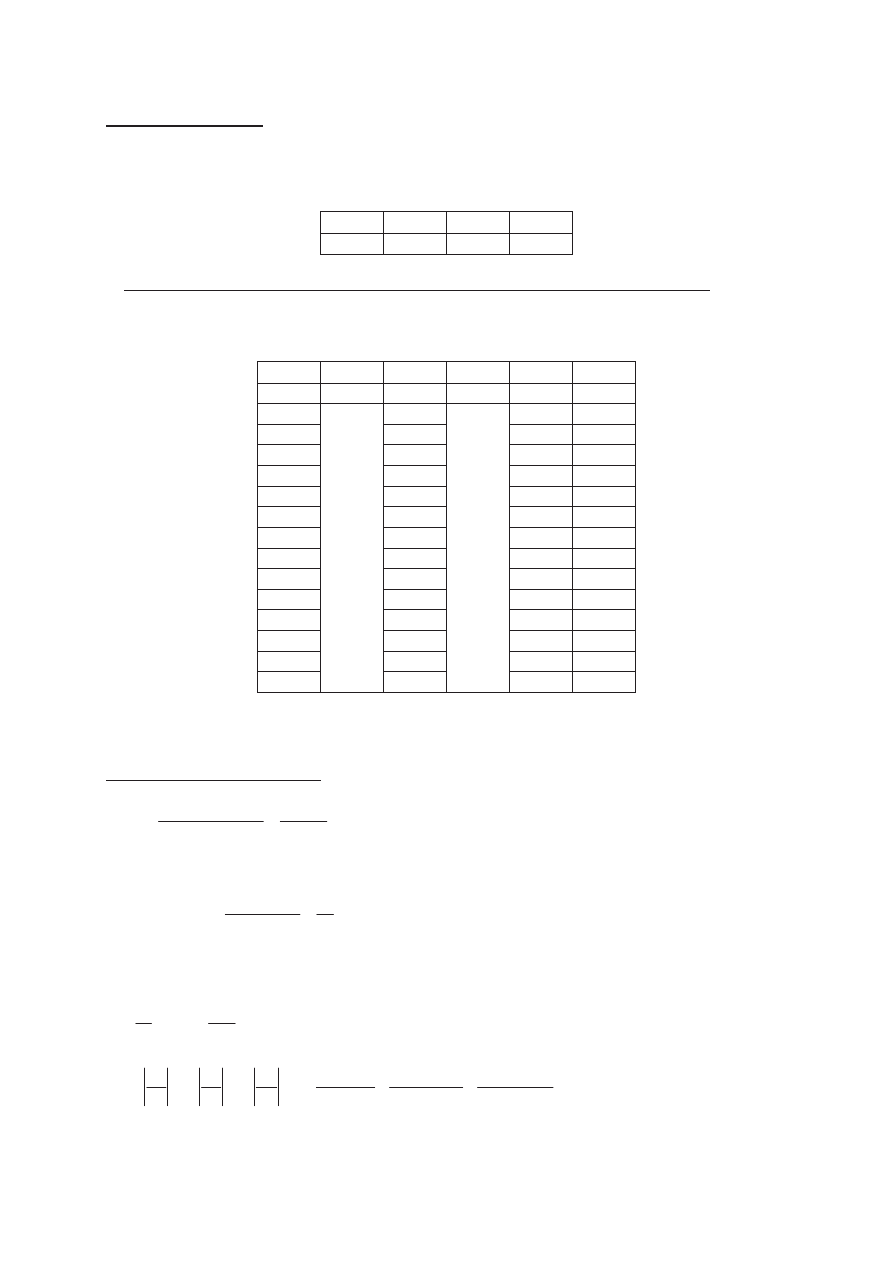
Pomiary do w/w zadaĔ wykonane zostały dla układu pomiarowego zaprezentowanego na Rysunku 2.

Rys. 2. Schemat układu pomiarowego

Pomiary i obliczenia

Pomiary zostały dokonane przy wykorzystaniu Zasilacza Stabilizowanego ZSC 05012 oraz urządzenia

LM-3, słuĪącego jako mikroamperomierz, którego klasa wynosi 0,5. ħródło Ğwiatła było zasilane przez prąd o
charakterystyce: I = 1,46 A, U = 8,84 V. PrzyjĊte do obliczeĔ wartoĞci zostały zaprezentowane poniĪej:

Tabela 1. WartoĞci przyjĊte do obliczeĔ

I [cd]

ǻ I [cd]

Į [ ˚ ]

ǻ Į [ ˚ ]

16,5

0,5

0

1

1. Wyznaczanie zaleĪnoĞci E=f(r)oraz charakterystyki Ğwietlnej fotoogniwa i=f (E)

Pomiary prądu zostały dokonane na zakresie 75, taką samą wartoĞü ma górna podziałka z której

korzystaliĞmy. Tabela 2 zawiera zestawione pomiary i wykonane obliczenia.

Tabela 2. Dane pomiarowe i obliczenia

r

ǻ r

i

ǻ i

E

ǻ E

[cm]

[cm]

[ȝA]

[ȝA]

[lx]

[lx]

30

66

183,33

6,78

35

48

134,69

4,85

40

36

103,13

3,64

45

28

81,48

2,83

50

22,5

66,00

2,26

55

18,5

54,55

1,85

60

15,5

45,83

1,54

65

13

39,05

1,30

70

11,5

33,67

1,12

75

10

29,33

0,97

80

9

25,78

0,85

85

8

22,84

0,75

90

7,5

20,37

0,66

95

0,2

7

0,5

18,28

0,59

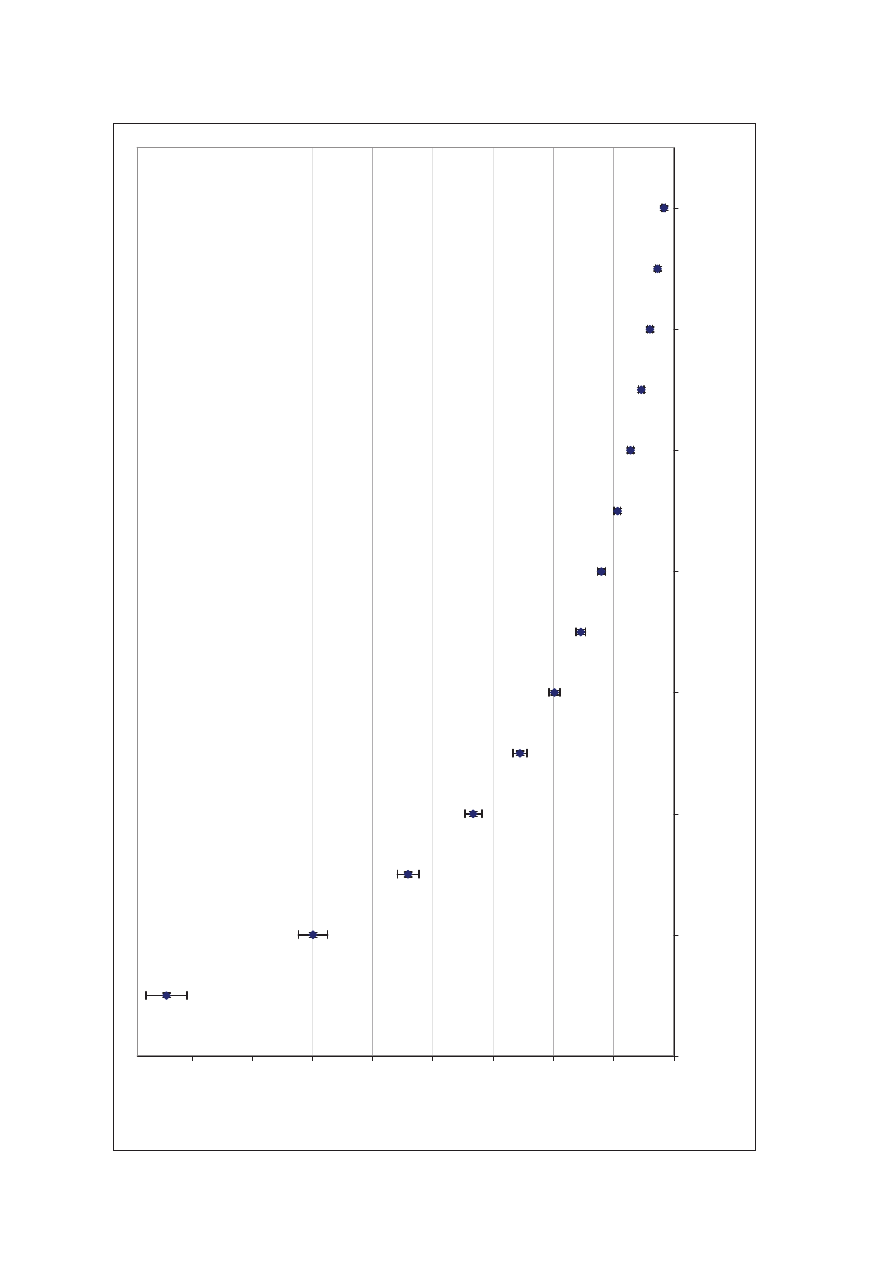
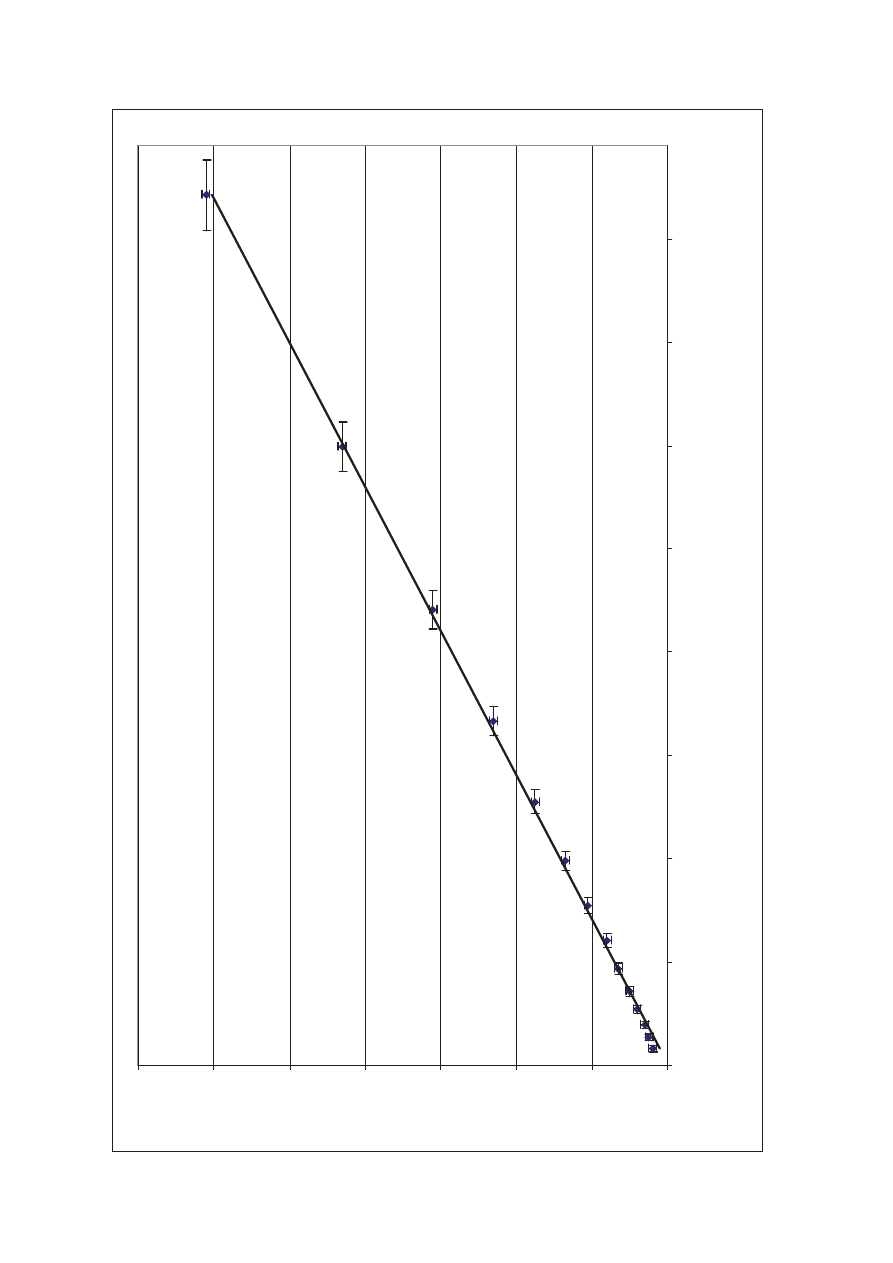
Na podstawie danych z tabeli został sporządzony wykres nr 1 tj. E=f(r) oraz wykres nr 2 tj. zaleĪnoĞü

i=f (E).

Wzory i przykładowe obliczenia

Przykładowe obliczenia zostały zaprezentowane dla pierwszego pomiaru:

A

zakres

klasa

klasy

µ

375

,

0

100

75

5

,

0

100

max

=

×

=

×

=

∆

A

odczyt

podział

i

A

podział

zakres

podział

A

A

a

elementarn

odczytu

a

elementarn

odczytu

klasy

odczytu

µ

µ

µ

µ

66

66

1

1

75

75

5

,

0

125

,

0

max

=

⋅

=

⋅

=

=

=

=

=

∆

+

∆

=

∆

=

∆

W oparciu o prawo Lamberta wyznaczamy natĊĪenie oĞwietlenia:

lx

r

I

E

33

,

183

1

3

,

0

5

,

16

cos

2

2

=

⋅

=

⋅

=

α

NiepewnoĞü E liczymy z róĪniczki zupełnej:

lx

r

I

r

r

I

r

I

E

r

r

E

I

I

E

E

78

,

6

sin

cos

cos

2

3

2

=

∆

⋅

⋅

+

⋅

∆

⋅

+

⋅

∆

=

∆

∂

∂

+

∆

∂

∂

+

∆

∂

∂

=

∆

α

α

α

α

α

α

Pozostałe obliczenia zostały wykonane analogicznie.

2. Wyznaczanie zaleĪnoĞci E=f(Į)

Pomiary zostały dokonane zgodnie z przedstawionym wczeĞniej opisem, przy nie zmienionych

parametrach zasilacza oraz z wykorzystaniem tej samej podziałki przyrządu LM-3 co poprzednio. Wyniki
pomiarów i obliczenia zostały uporządkowane w Tabeli 3.

Tabela 3. Dane pomiarowe

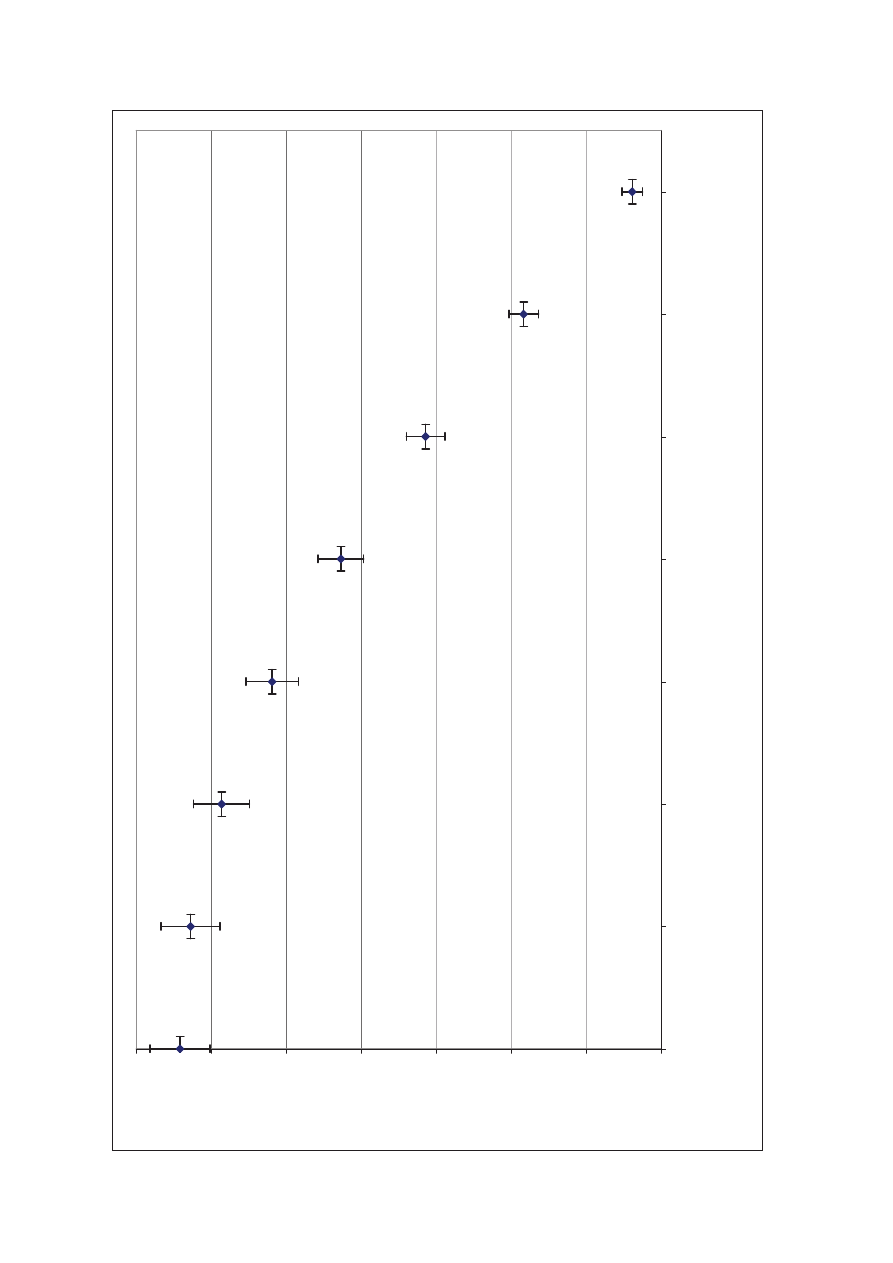
PowyĪsze dane posłuĪyły do wykreĞlenia Wykresu 3, tj. zaleĪnoĞci E=f(Į). Wykres bĊdzie siĊ opierał

na danych uzyskanych za pomocą prawa Lamberta.

Wzory i przykładowe obliczenia

Przykładowe obliczenia zawierają tylko wzory, które pojawiły siĊ pierwszy raz. Obliczenia

przeprowadzono dla kąta Į=10˚.

lx

r

I

E

zLamberta

33

,

183

10

cos

3

,

0

5

,

16

cos

2

2

=

⋅

=

⋅

=

$

α

E

z charakt

było liczone poprzez wyznaczenie z trendu liniowego, zaznaczonego na Wykresie 2, zmiennej

x i podstawienie odpowiednich wartoĞci.

lx

i

E

87

,

186

3587

,

0

5283

,

0

5

,

66

3587

,

0

5283

,

0

=

+

=

+

=

NiepewnoĞü E została wyznaczona metodą pochodnej logarytmicznej. Prezentowane obliczenie

niepewnoĞci dotyczy natĊĪenia oĞwietlenia uzyskanego z prawa Lamberta.

lx

E

r

r

I

I

E

00

,

8

33

,

183

3

,

0

002

,

0

2

5

,

16

5

,

0

2

=

⋅

¸¸

¹

·

¨¨

©

§

⋅

+

=

⋅

¸

¹

·

¨

©

§

∆

+

∆

=

∆

3. Badanie przepuszczalnoĞci filtrów szarych

Przy ustalonej odległoĞci r = 30 cm fotoogniwa od Ĩródła Ğwiatła oraz przy prostopadłym padaniu

promieni Ğwietlnych na czynną powierzchniĊ fotoogniwa zmierzyliĞmy natĊĪenie prądu fotoelektrycznego i.
Wyniosło ono 69 ȝA. NastĊpnie, na drodze promieni Ğwietlnych umieszczaliĞmy po kolei filtry szare i
mierzyliĞmy natĊĪenie prądu fotoelektrycznego i’ dla strumienia Ğwiatła przepuszczanego przez filtr.

Tak zebrane dane zostały zaprezentowane w Tabeli 4.

Tabela 4. Dane pomiarowe – przepuszczalnoĞü filtrów

nr filtra

i'

delta i'

T

elta T

1

30,0

0,4348

0,0104

4

16,5

0,2391

0,0090

5

8,5

0,1232

0,0081

6

4,5

0,5

0,0652

0,0077

Į

i

Į

i

i

Ğ

r

ǻ i

E

z Lamberta

E

z charakt

ǻ E

z Lamberta

ǻ E

z charakt

[ ˚ ]

[ȝA]

[ ˚ ]

[ȝA]

[ȝA]

[ȝA]

[lx]

[lx]

[lx]

[lx]

0

66,5

0

66,5

66,50

183,33

186,87

8,00

8,15

10

64,0

-10

60,5

62,25

180,55

175,02

7,88

7,64

20

63,0

-20

56,0

59,50

172,28

167,35

7,52

7,30

30

61,5

-30

53,5

57,50

158,77

161,77

6,93

7,06

40

56,5

-40

44,0

50,25

140,44

141,56

6,13

6,18

50

48,0

-50

39,0

43,50

117,84

122,74

5,14

5,36

60

41,0

-60

28,5

34,75

91,67

98,35

4,00

4,29

70

31,0

-70

16,0

23,50

0,5

62,70

66,99

2,74

2,92

A

i

Ğ

r

µ

25

,

62

2

5

,

60

0

,

64

=

+

=

Wzory i przykładowe obliczenia

Obliczenia dotyczą filtru nr 1. Współczynnik przepuszczalnoĞci filtra wyznaczamy ze wzoru:

4348

,

0

69

30

'

=

=

=

i

i

T

NiepewnoĞü współczynnika liczymy metodą róĪniczki zupełnej.

0104

,

0

'

'

'

'

2

=

∆

⋅

+

∆

=

∆

∂

∂

+

∆

∂

∂

=

∆

i

i

i

i

i

i

i

T

i

i

T

T

Dla pozostałych filtrów obliczenia przebiegały analogicznie.

4. Wyznaczanie mocy dostarczonej do Īarówki

Z wykonanych pomiarów jesteĞmy w stanie obliczyü jedynie moc dostarczona do Īarówki przy

wykonywaniu powyĪszych üwiczeĔ. ħródło Ğwiatła było zasilane przez prąd o charakterystyce odczytanej z
zasilacza: I = 1,46 A, U = 8,84 V. Jako, Īe mieliĞmy do dyspozycji dokładniejsze przyrządy pomiarowe,
skorzystaliĞmy z nich. NatĊĪenie mierzone było przyrządem MASTER M890G na zakresie 20 A, a napiĊcie
przyrządem METEX-3800 na zakresie 20 V.

Dane niezbĊdne do obliczeĔ:

•

dokładnoĞü Multimetru MASTER M890G

± 0,3 % rdg + 1 dgt

•

dokładnoĞü Multimetru METEX-3800

± 2,0 % rdg + 5 dgt

Obliczenia zostały zebrane w Tabeli 5.

Tabela 5. Dane pomiarowe – obliczenie mocy

I

ǻ I

U

ǻ U

M

ǻ M

A

A

V

V

W

W

1,47

0,01

8,77

0,23

12,89

0,46

Wzory i przykładowe obliczenia

Moc obliczymy korzystając ze wzoru M = U *

I = 1,47 A * 8,77 V = 12,89 W.

NiepewnoĞci napiĊcia i natĊĪenia liczymy z dokładnoĞci Multimetrów:

V

U

A

I

23

,

0

05

,

0

77

,

8

*

02

,

0

01

,

0

01

,

0

47

,

1

*

003

,

0

=

+

=

∆

=

+

=

∆

NiepewnoĞü mocy liczymy metodą róĪniczki zupełnej:

W

I

U

U

I

M

46

,

0

01

,

0

*

77

,

8

23

,

0

*

47

,

1

*

*

=

+

=

∆

+

∆

=

∆

CZ.II Wizualne pomiary fotometryczne z wykorzystaniem fotometru Lummera –

Brodhuna

Układ i metody pomiarowe

Podczas wykonywania

üwiczenia korzystaliĞmy z fotometru Lummera-Brodhuna, którego schemat jest

zaprezentowany poni

Īej

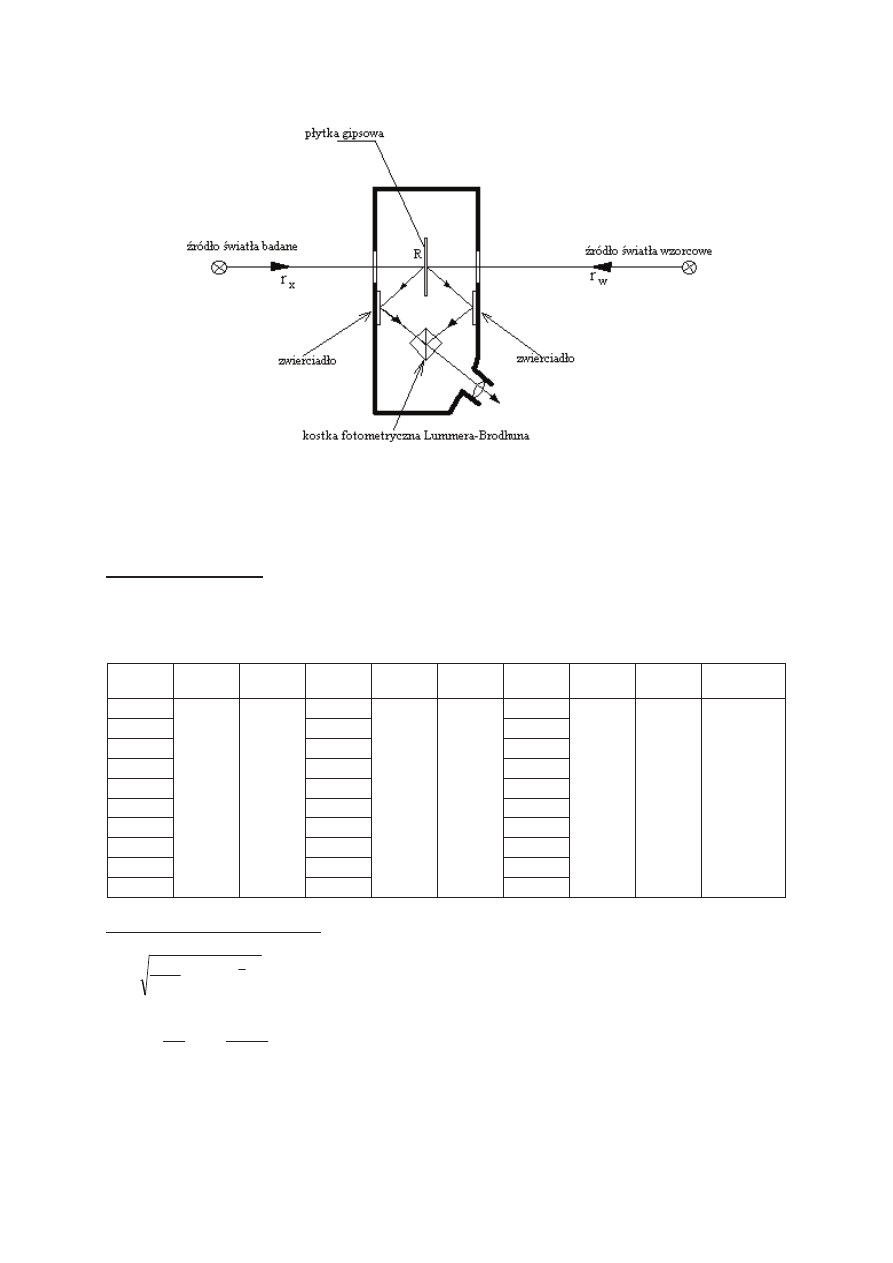
Rys. 3. Schemat układu pomiarowego

Subiektywne pomiary fotometryczne są oparte na porównywaniu oĞwietlenia z dwóch Ĩródeł

równoczeĞnie. BĊdziemy takiego szukaü takiego połoĪenia głowicy fotometru dla którego nie bĊdziemy w stanie
zauwaĪyü róĪnicy w oĞwietleniu pola widzenia.

Pomiary i obliczenia

W celu wyznaczenia natĊĪenia Ĩródła Ğwiatła wykonaliĞmy 10 pomiarów dla których było spełnione

w/w załoĪenie. ĩarówka wzorcowa wykorzystana w üwiczeniu miała moc 40 W. Uporządkowane pomiary
zostały zebrane w Tabeli 6.

Tabela 6. Dane pomiarowe – fotometrLummera-Brodhuna

r

w

[cm]

r

w

Ğr

[cm]

ǻ r

w

Ğr

[cm]

r

x

[cm]

r

x

Ğr

[cm]

ǻ r

x

Ğr

[cm]

I

b

[cd]

I

b

Ğr

[cd]

ǻ I

b

Ğr

[cd]

ǻ I

b

Ğr / I

b

Ğr

[%]

129,60

120,40

23,30

129,80

120,20

23,15

130,50

119,50

22,64

130,50

119,50

22,64

130,80

119,20

22,42

130,20

119,80

22,86

130,40

119,60

22,71

129,90

120,10

23,08

130,30

119,70

22,79

130,20

130,22

0,36

119,80

119,78

0,36

22,86

22,85

0,27

1,17

Wzory i przykładowe obliczenia

NiepewnoĞci wartoĞci Ğrednich obliczono przy pomocy odchylenia standardowego.

¦

=

−

−

=

n

i

x

i

x

n

x

s

1

2

)

(

1

1

Natomiast natĊĪenie badanego Ĩródła ze wzoru:

cd

r

r

I

I

w

b

w

b

3

,

23

4

,

120

6

,

129

27

2

2

2

2

=

⋅

=

⋅

=

1

5

3

5

5

5

7

5

9

5

1

1

5

1

3

5

1

5

5

1

7

5

2

5

3

5

4

5

5

5

6

5

7

5

8

5

9

5

o

d

le

g

ło

Ğü

r

nat

ĊĪe

nie

o

Ğw

iet

len

ia

E

W

yk

re

s

1

.

Z

a

le

Īn

o

Ğü

E

=

f(

r)

y

=

0

,3

5

8

7

x

-

0

,5

2

8

6

R

2

=

0

,9

9

9

5

1

5

2

5

3

5

4

5

5

5

6

5

7

5

1

5

,0

0

3

5

,0

0

5

5

,0

0

7

5

,0

0

9

5

,0

0

1

1

5

,0

0

1

3

5

,0

0

1

5

5

,0

0

1

7

5

,0

0

na

tĊ

Īe

ni

e

o

Ğw

ie

tle

ni

a

E

prą

d f

oto

ele

ktr

ycz

ny

i

W

yk

re

s

2

.

C

h

a

ra

kt

er

ys

ty

ka

Ğ

w

ie

tl

n

a

f

o

to

o

g

n

iw

a

s

el

en

o

w

eg

o

5

5

7

5

9

5

1

1

5

1

3

5

1

5

5

1

7

5

1

9

5

0

1

0

2

0

3

0

4

0

5

0

6

0

7

0

k

ąt

Į

nat

ĊĪe

nie

o

Ğw

iet

len

ia

E

W

yk

re

s

3

.

Z

a

le

Īn

o

Ğü

E

=

f(

Į

)

Wnioski koĔcowe

Celem zadania było zapoznanie siĊ z dwoma metodami pomiarów fotometrycznych. Subiektywną oraz

fizyczną. W pierwszej metodzie korzystaliĞmy z fotoogniwa. Na podstawie wykonanych doĞwiadczeĔ
stworzyliĞmy wykres E=f(r) (Wykres 1). DziĊki niemu moĪemy oceniü prawdziwoĞü fotometrycznego prawa
odległoĞci. Widzimy zatem Īe wykres poprawnie obrazuje zaleĪnoĞü wynikającą z tego prawa. Konkluzją moĪe
byü stwierdzenie, Īe nasze Ĩródło Ğwiatła moĪemy uznaü za punkowe, gdyĪ tylko dla punktowych Ĩródeł prawo
to jest zachowane.

Dla potwierdzenia naszych przypuszczeĔ przyjrzyjmy siĊ charakterystyce fotoogniwa (Wykres 2).

ZaleĪnoĞü ta jest prawie idealnie liniowa, wyjątek stanowią jedynie małe wartoĞci r, dla których liniowoĞü nie
jest zachowana. Wniosek: niespełniona liniowoĞü oznacza brak Ĩródła punktowego. Tak wiĊc mimo, Īe
charakterystykĊ cechuje wysoki współczynnik liniowoĞci musimy mieü na uwadze, Īe nie fotometryczne prawo
odległoĞci, nie jest zachowane dla małych r.

NastĊpnym wykresem przez nas wykreĞlonym jest zaleĪnoĞü E=f(Į). MoĪe on posłuĪyü jako dowód

prawa Lamberta, które mówi: ĞwiatłoĞü powierzchni promieniującej w wszystkich kierunkach zmienia siĊ
zgodnie z kosinusem kąta promieniowania. Z wykresu widzimy, Īe im wiĊkszy kąt padania promieni na
fotoogniwo, tym mniejszy cosinus tego kąta, a co za tym idzie mniejsza luminacja. Prawo Lamberta zostało wiĊc
potwierdzone doĞwiadczalnie.

Podczas pomiarów do tej czĊĞci zadania warto zwróciü uwagĊ, Īe otrzymane wyniki dla wychylenia

fotoogniwa w prawo i w lewo nie były sobie równe. Spowodowane to było wystĊpowaniem róĪnych
powierzchni po obu stronach fotoogniwa. KaĪda z tych powierzchni charakteryzowała siĊ róĪna luminacją. I tak
dla wychylenia w prawo (znajdował siĊ tam czarny ekran odgradzający stanowiska) iloĞü Ğwiatła jaka padała na
ekran fotoogniwa jest wiĊksza.

Metoda subiektywna jest metodą mniej dokładną niĪ fizyczne pomiary. Wpływ na to miała głównie

czułoĞü ludzkiego oka oraz subiektywne odczucia równoĞci natĊĪenia Ğwiatła osób robiących pomiary. Mimo, Īe
w naszym przypadku pomiary wykonywane przez 4 osoby wyszły bardzo zbliĪone do siebie to skłaniamy siĊ
jednak to metody fizycznej, jako tej dokadniejszej. Dodatkowym plusem przemawiającym za nią jest wiĊksza
łatwoĞü skorzystania z niej w miejscu innym niĪ pracownie LPF.