Sortowanie „szybkie”

Quick_Sort

Tony Hoare (1960)

Algorytm sortowania

QuickSort

Cechy algorytmu:

Przeciętna złożoność obliczeniowa O(nlgn),

Pesymistyczna złożoność O(n

2

),

Sortowanie „w miejscu”,

Niestabilny,

Zastosowanie techniki „dziel i zwyciężaj”,

Algorytm rekurencyjny.

Rozproszone sortowanie,

Wpływ danych wejściowych na złożonoość obliczeniową,

Łatwa implementacja,

Sprawdza się w sortowaniu średnich i dużych zbiorów danych.

ASD

LJ

S

Algorytm sortowania

QuickSort

Podstawowy etap algorytmu:

1.

Wybór elementu osiowego (dzielącego) (

pivotpoint

) v=A[q],

2.

Pogrupowanie elementów tablicy A[lewy.. prawy] w sposób następujący:

żaden z elementów A[lewy], ..., A[q-1] „nie większy” niż v,

żaden z elementów A[q+1], ..., A[prawy] „nie mniejszy” niż v,

ASD

LJ

S

Warianty schematu algorytmu:

Rekurencyjny, nierekurencyjny

Wybór elementu osiowego:

pierwszy, środkowy lub ostatni,

losowy,

mediana z 3.

Algorytm

QuickSort

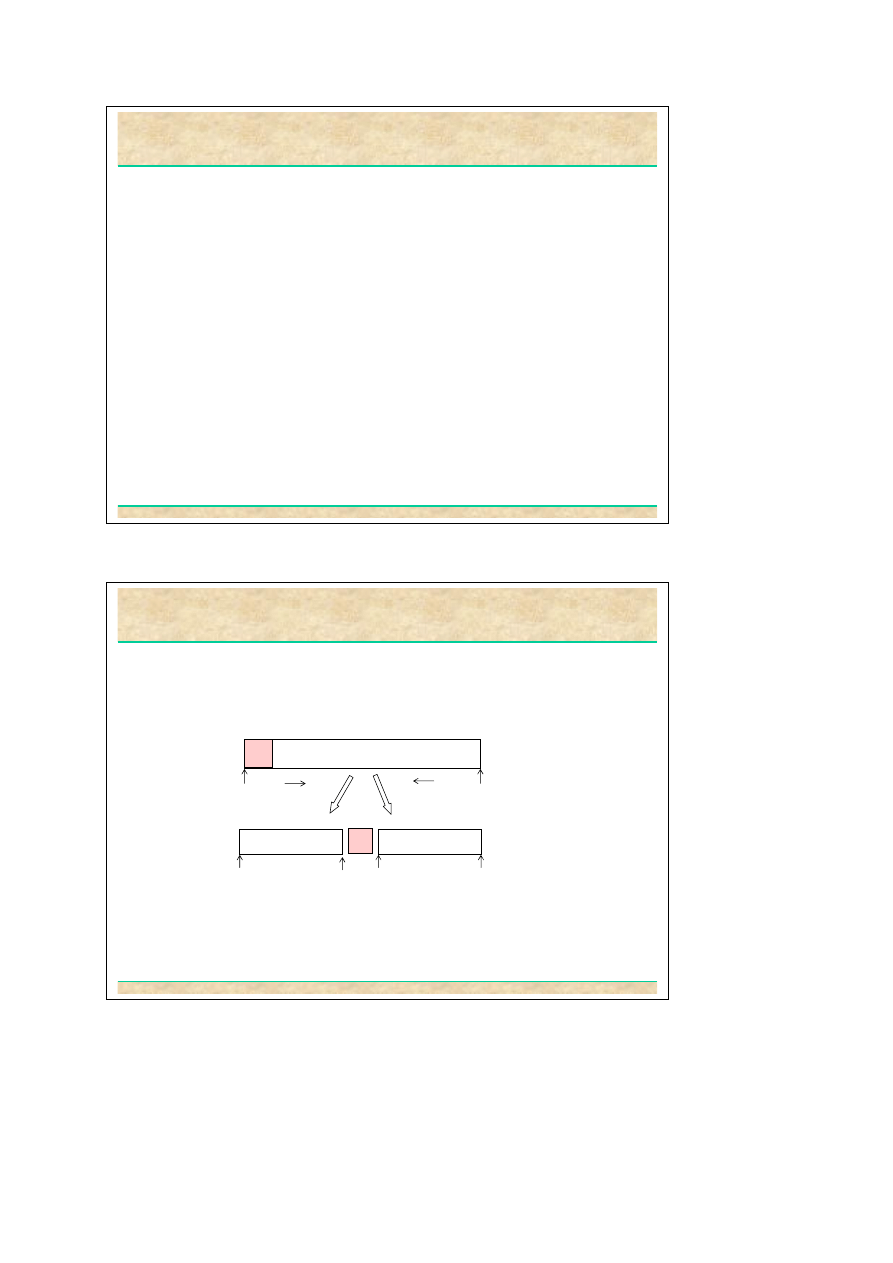
Zakładając, że wybierany jest element osiowy jako pierwszy element tablicy tj.

v=A[lewy] otrzymujemy podział:

v

lewy

prawy

i

j

elementy ≤ v

elementy ≥ v

v

lewy

prawy

prawy

lewy

Dzielenia tablicy dokonuje procedura podziału (

partition

).

ASD

LJ

S

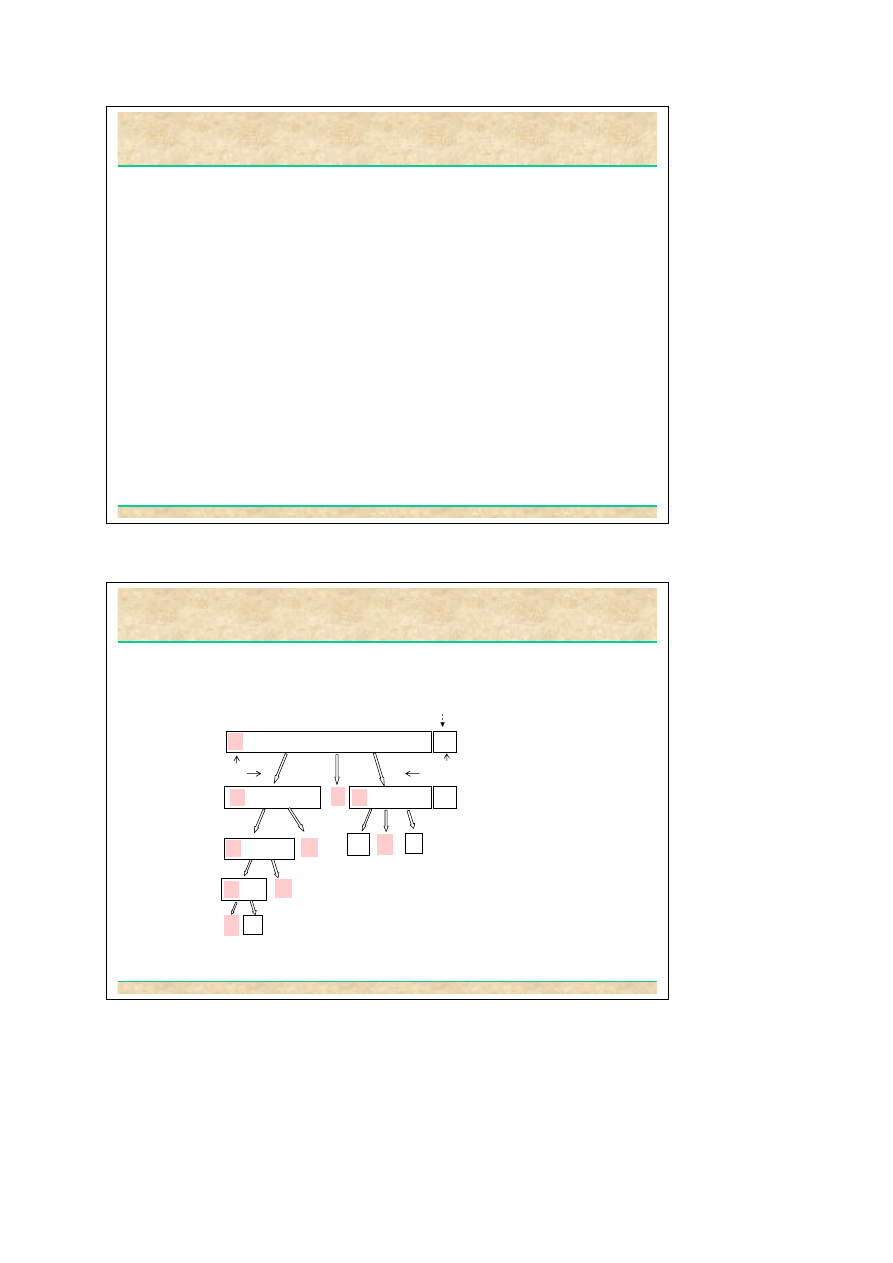
Algorytm sortowania

QuickSort

Działanie procedury podziału (element osiowy A[lewy]):

1.

Wybór elementu osiowego np. v=A[lewy] dzielącego tablicę A[lewy..prawy],

2.

Przeglądanie A[lewy+1],;,A[prawy] od strony lewej, dopóki nie zostanie

znaleziony element „większy równy” od v,

3.

Przeglądanie A[lewy+1],;,A[prawy] od strony prawej, dopóki nie zostanie
znaleziony element „mniejszy równy” od v,

4.

Dwa elementy, na których się zatrzymują się indeksy, wymieniane są
miejscami. Przeszukiwanie kontynuuowane jest od lewej a później od prawej,

5.

Kiedy indeksy się spotkają proces podziału kończy się,

6.

Element osiowy v zamieniany jest z ostatnim elementem lewej części tablicy.

ASD

LJ

S

Algorytm sortowania

QuickSort

Mechanizm sortowania:

3

7

4

8

5

2

9

i

∞

∞

∞

∞

6

j

3

2

4

5

7

9

∞

∞

∞

∞

8

6

3 2

9

8

7

5

4

4

3

2

2

3

wartownik

ASD

LJ

S

Algorytm sortowania

QuickSort

Partition(A,lewy,prawy)

{//użycie wartownika A[prawy+1]=

+∞ ;

v=A[lewy];
i=lewy;
j=prawy+1;
DO{

DO i=i+1; WHILE (A[i]<v);
DO j=j-1; WHILE (A[j]>v);
IF (i<j) swap(A[i],A[j]);

} WHILE(i<j)
A[lewy]=A[j];
A[j]=v;
return(j);

}

QuickSort(A,lewy,prawy)
{

q=Partition (A,lewy,prawy);
IF(q-1>lewy)QuickSort(A,lewy,q-1);
IF(q+1<prawy)QuickSort(A,q+1,prawy);

}

ASD

LJ

S

Mechanizm sortowania:

Algorytm sortowania

QuickSort

QuickSort(A,lewy,prawy)
{

q=Partition (A,lewy,prawy);
IF(q-1>lewy)QuickSort(A,lewy,q-1);
IF(q+1<prawy)QuickSort(A,q+1,prawy);

}

ASD

LJ

S

Partition(A,lewy,prawy)
{

v=A[prawy];
i=lewy-1;
FOR (j=lewy; j≤prawy-1; j=j+1)

IF (A[j]≤v){

i=i+1;
swap(A[i],A[j]);

}

swap(A[i+1],A[prawy]);
return(i+1);

}

Złożoność algorytmu

QuickSort

Złożoność obliczeniowa algorytmu zależy od zrównoważenia podziałów tablicy:

Podział niezrównoważony

Podział zrównoważony

Podział niezrównoważony (przypadek najgorszy) - żaden element nie zostaje

umieszczony po lewej stronie elementu osiowego przez procedurę podziału.

Podział zrównoważony (przypadek najlepszy) - gdy element osiowy dzieli tablicę

na dwie równe części.

ASD

LJ

S

Złożoność algorytmu

QuickSort

Pesymistyczna złożoność (podział niezrównoważony).

Podział niezrównoważony - gdy procedura Partition tworzy dwie podtablice:

1-elementową

(n-1) elementową

Po prawej stronie, elementu osiowego otrzymujemy tablicę pomniejszoną tylko o

jeden element.

Zakładamy, że podziały niezrównoważone będą wykonywane w każdym kroku

algorytmu.

ASD

LJ

S

Złożoność algorytmu

Sortowanie tablicy
n -elementowej

Podział tablicy

T(n) = T(1) + T(n-1) + T

part

(n)

Sortowanie
tablicy (n-1)-elementowej

Sortowanie tablicy
1-elementowej
T(1)=0

Złożoność pesymistyczna

:

ASD

LJ

S

Złożoność procedury Partition.

Rozmiar danych wejściowych n=prawy–lewy +1

T

part

(n) = n-1 = Θ(n)

Złożoność algorytmu

Złożoność czasowa procedury Partition.

T(n) = T(n-1) + Θ(n) = T(1) + ∑

n-1

k=1

Θ(k) =

Θ

(1) + ∑

n -1

k=1

Θ(k) = Θ(∑

n-1

k=1

k) = Θ(n

2

)

0

n = 1

T(n-1) + (n-1)

n > 1

T(n) =

Rozmiar danych wejściowych n=prawy–lewy +1

T

part

(n) = n-1 = Θ(n)

Pesymistyczna złożoność sortowania (podział niezrównoważony).

Θ(1)

n = 1

T(n-1) + Θ(n)

n > 1

T(n) =

ASD

LJ

S

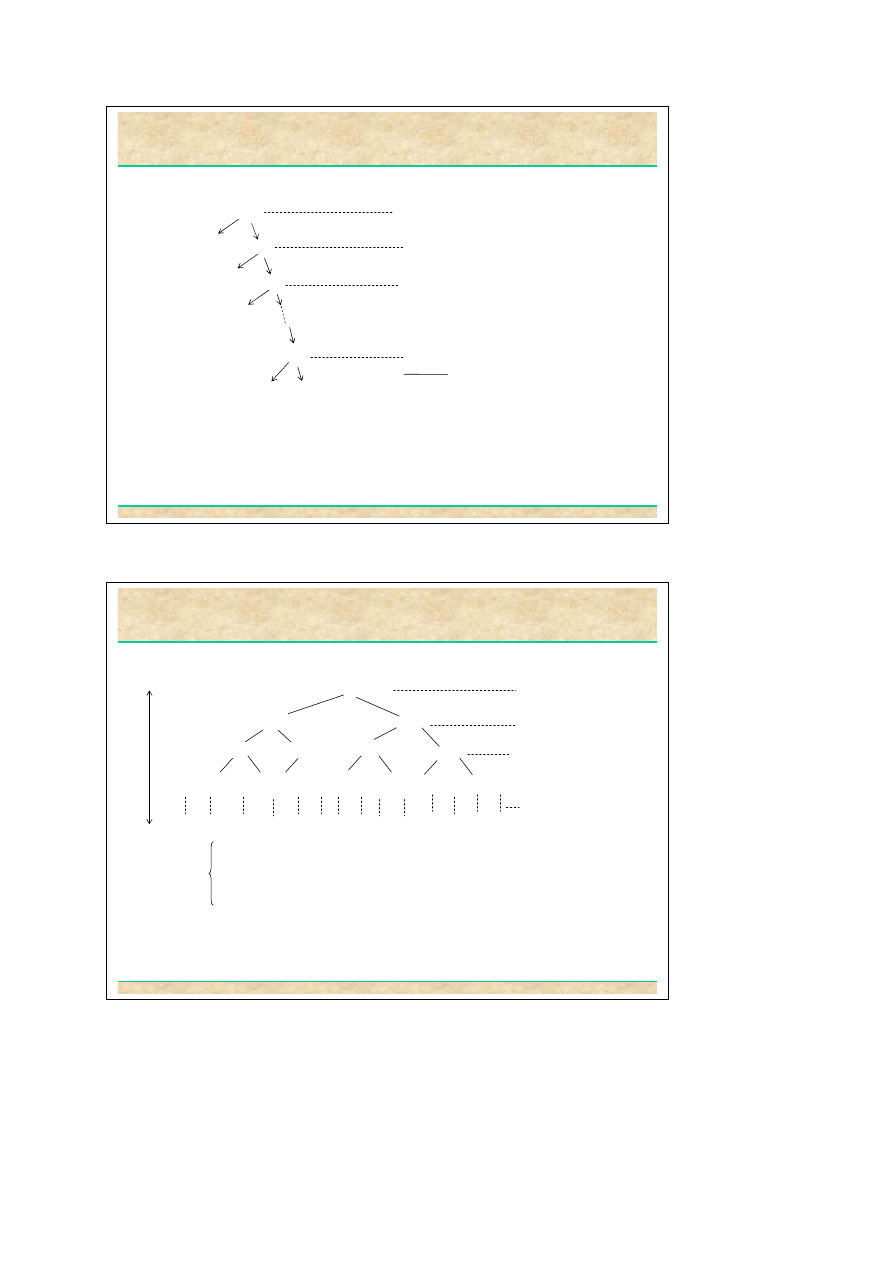
Podział niezrównoważony

Drzewo rekurencji:

1

n-2

1

n-1

1

2

1

n

1

(n-1)

(

n-2

)

(

n-3

)

1

T(n) = 1+ 2+ ... +(n-1) = n(n-1)/2 = Θ(n

2

)

Θ(n

2

)

ASD

LJ

S

Podział zrównoważony

Zrównoważone drzewo podziału:

T(n) = lgn Θ(n) = Θ(n lgn)

n

n/2

n/2

n/4

n/4

n/4

n/4

1

1

1

1

1

1 1

11

1

1 1

1

1

1

lgn
podziałów

Θ(n)

Θ(n)

Θ(n)

Θ(1)

n = 1

2T(n/2) + Θ(n)

n > 1

T(n) =

Rozwiązaniem równania jest T(n) = Θ(n lgn)

ASD

LJ

S

Złożoność algorytmu

QuickSort

0

dla n = 1

T(n) =

2 T(n/2) + (n – 1)

dla n > 1

T(n) = 2

k

T(n/2

k

) + 2

k-1

(n/2

k-1

-1) + 2

k-2

(n/2

k-2

-1) + ... + 2

1

(n/2 -1) + 2

0

(n -1) =

= (n - 2

k-1

) + (n - 2

k-2

) + ...+ (n - 2

-1

) + (n -1) =

= k n – (1+2+...+2

k-1

) = kn – ((2

k

-1) / (2-1)) = kn – (2

k

– 1) =

= nlgn – (n-1)

T(n) = O(nlgn)

Złożoność algorytmu (podział zrównoważony).

ASD

LJ

S

Złożoność algorytmu

QuickSort

Poprawność rozwiązania:

T(n) = nlgn – n+1

T(2n) = 2n lg(2n) - 2n + 1 = 2n(lg2 + lgn) – 2n + 1 =

= 2nlgn + 1 = 2(nlgn – n +1)+ 2n -2 +1 =

= 2T(n) + 2n -1

T(2n) = 2T(n) + 2n - 1

T(n) = Θ(n lgn)

ASD

LJ

S

Złożoność algorytmu QuickSort

Przeciętna złożoność obliczeniowa algorytmu.

partition

procedury

realizacji

czas

j

n

T

j

T

n

n

n

T

ave

ave

n

j

ave

↑

−

+

−

+

−

=

∑

=

))

(

)

1

(

(

1

)

1

(

)

(

1

Równanie rekurencyjne:

- prawdopodobieństwo tego, że zwracana przez procedurę partition

wartość jest równa j.

n

1

)

(

log

log

2

)

(

n

O

n

n

e

n

T

ave

+

=

log ≡ log

10

ASD

LJ

S

Wrażliwość algorytmu QuickSort

Pesymistyczna wrażliwość czasowa algorytmu:

∆(n)=O(n

2

- nlgn) = O(n

2

)

Oczekiwana wrażliwość czasowa:

68

.

0

)

(log

)

3

2

7

(

)

(

2

↓

+

−

=

n

O

n

n

π

σ

ASD

LJ

S

Sortowanie przez scalanie

Merge_Sort

John von Neumann

Sortowanie przez scalanie

ASD

LJ

S

Cechy algorytmu:

Złożoność obliczeniowa O(nlgn),

Stabilny,

Sortowanie ekstensywne,

Zastosowanie techniki „dziel i zwyciężaj”,

Algorytm rekurencyjny,

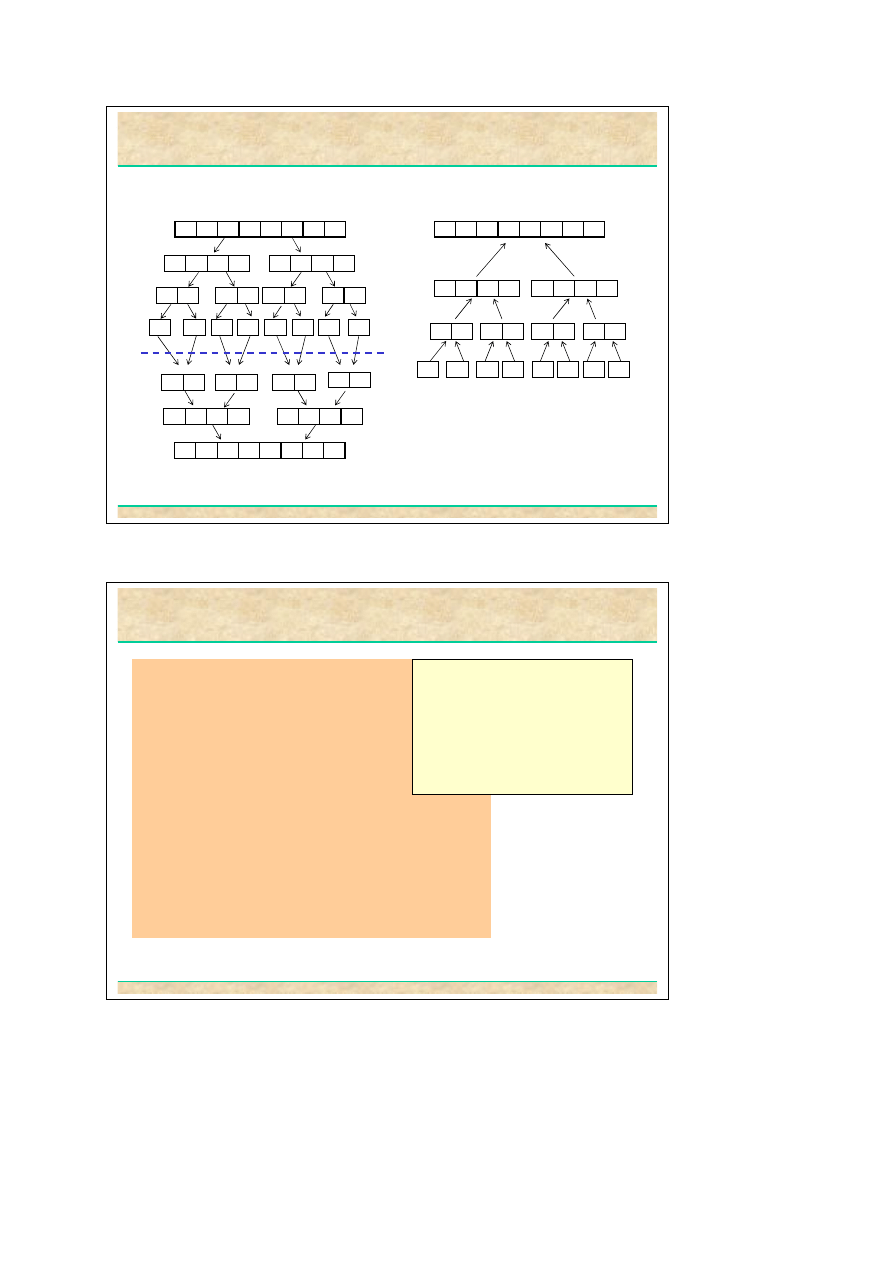
Sortowanie przez scalanie

5

2

4

6

1

3

2

6

5

2

4

6

1

3

2

6

5

2

4

6

1

3

2

6

5

2

4

6

1

3

2

6

2

5

4

6

1

3

2

6

2

4

5

6

1

2

3

6

1

2

2

3

4

5

6

6

1

2

2

3

4

5

6

6

2

4

5

6

1

2

3

6

2

5

4

6

1

3

2

6

5

2

4

6

1

3

2

6

Idea algorytmu mergeSort.

ASD

LJ

S

Sortowanie przez scalanie

Merge (A,lewy,q,prawy)
{ // B-tablica pomocnicza

i=lewy;
j=q+1;
k=1;
WHILE(i≤q and j≤prawy) {

IF(A[i]<A[j]){
B[k]=A[i];
i=i+1;
}ELSE{

B[k]=A[j]);
j=j+1;

}
k=k+1;

}
IF(i>q )

Kopiuj A[j],...,A[prawy] do B[k],...,B[prawy];

ELSE

Kopiuj A[i],...,A[q] do B[k],...,B[prawy];

Kopiuj B[lewy],...,B[prawy] do A[lewy],...,A[prawy];

}

MergeSort (A, lewy, prawy)
{

IF(lewy<prawy){

q:= (lewy+prawy)/2
MergeSort (A,lewy,q)
MergeSort (A,q+1,prawy)
Merge (A,lewy,q,prawy)

}

}

ASD

LJ

S

Złożoność algorytmu

MergeSort

16

8

8

4

4

4

4

1

1

1

1

1

1 1

11

1

1

1

1

1

1

1

1

10

5

5

3

2

3

2

1

1

1

1

1

2

2

1

1

1

1

1

Drzewa podziału algorytmu Merge_sort.

ASD

LJ

S

Złożoność algorytmu

MergeSort

Θ(1)

dla n = 1

T(n) =

2 T(n/2) + Θ(n)

dla n > 1

0

dla n = 1

T(n) =

2 T(n/2) + (n – 1)

dla n > 1

ASD

LJ

S

Złożoność algorytmu

MergeSort

Θ(1)

dla n = 1

T(n) =

2 T(n/2) + Θ(n)

dla n > 1

0

dla n = 1

T(n) =

2 T(n/2) + (n – 1)

dla n > 1

T(n) = 2

k

T(n/2

k

) + 2

k-1

(n/2

k-1

-1) + 2

k-2

(n/2

k-2

-1) + ... + 2

1

(n/2 -1) + 2

0

(n -1) =

= (n - 2

k-1

) + (n - 2

k-2

) + ...+ (n - 2

-1

) + (n -1) =

= k n – (1+2+...+2

k-1

) = kn – ((2

k

-1) / (2-1)) = kn – (2

k

– 1) =

= nlgn – (n-1).

T(n) =

Θ

(nlgn)

ASD

LJ

S

Złożoność algorytmu

MergeSort

Poprawność rozwiązania:

T(n) = nlgn – n+1

T(2n) = 2n lg(2n) - 2n + 1 = 2n(lg2 + lgn) – 2n + 1 =

= 2nlgn + 1 = 2(nlgn – n +1)+ 2n -2 +1 =

= 2T(n) + 2n -1

T(2n) = 2T(n) + 2n - 1

T(n) = Θ(n lgn)

ASD

LJ

S