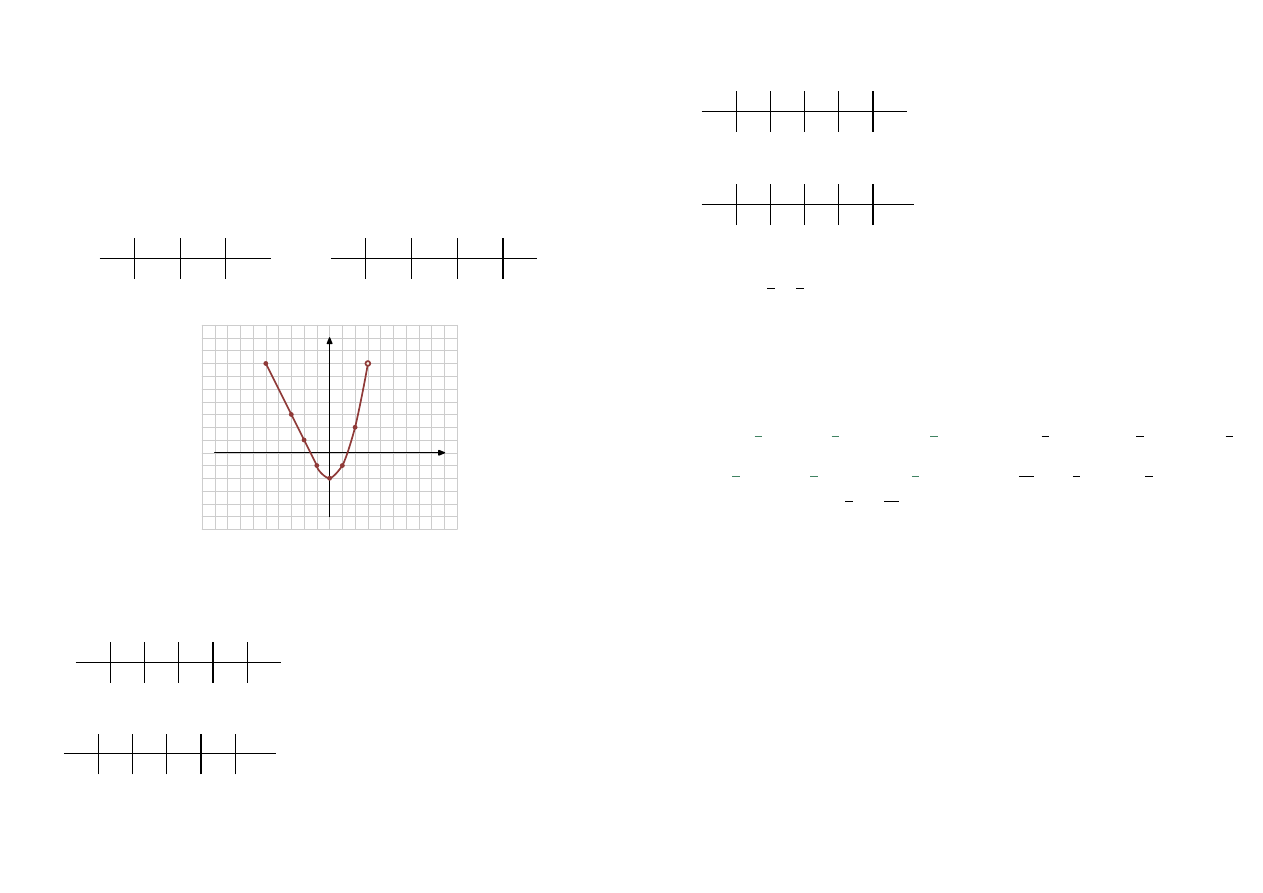
materiał pochodzi ze strony
Narysuj wykres następującej funkcji.
f (x) =
−2x − 3
dla
x ∈ h−5, −1)
x
2
− 2
dla
x ∈ h−1, 3)
Rozwiązanie
:
y = −2x − 3
y = x
2
− 2
x
−5
−3
−2
y
7
3
1
x
−1
0
1
2
y
−1
−2
−1
2
x
y
Czy następujące określone tabelką przyporządkowania są funkcjami?
Rozwiązanie:
x
1
3
7
2
8
y
4
8
9
0
1
To przyporządkownie jest
, ponie-
waż każdej liczbie ze zbioru
x
-ów jest przy-
porządkowana dokładnie jedna liczba ze
zbioru
y
-ów.
x
2
3
5
8
9
y
1
4
1
1
10
To przyporządkownie jest
, ponie-
waż każdej liczbie ze zbioru
x
-ów jest przy-
porządkowana dokładnie jedna liczba ze
zbioru
y
-ów. Nie szkodzi, że wartość
1
po-
wtarza się trzy razy.
x
4
5
4
7
8
y
2
3
5
0
1
To przyporządkownie nie jest
, po-
nieważ liczbie
4
zostały przyporządkowane
dwie liczby
2
i
5
.
x
1
1
1
3
2
y
0
2
8
9
12
To przyporządkownie nie jest
, po-
nieważ liczbie
1
zostały przyporządkowane
trzy liczby
0
,
2
i
8
.
Funkcja jest określona wzorem
f (x) = x
2
− 3x + 5
. Oblicz jej wartości dla argumentów
4
,
0
,
−4
,
1 +
√
2
,
3
√
5 − 2
.
Rozwiązanie
:
f (
4
) =
4
2
− 3 ·
4
+ 5 = 16 − 12 + 5 = 9
f (
0
) =
0
2
− 3 ·
0
+ 5 = 5
f (
−4
) = (
−4
)
2
− 3 · (
−4
) + 5 = 16 + 12 + 5 = 33
f (
1 +
√
2
) = (
1 +
√
2
)
2
− 3 · (
1 +
√
2
) + 5
= 1 + 2
√
2 + 2 − 3 − 3
√
2 + 5 = 5 −
√
2
f (
3
√
5 − 2
) = (
3
√
5 − 2
)
2
− 3 · (
3
√
5 − 2
) + 5
=
3
√
25 − 4
3
√
5 + 4 − 3
3
√
5 + 6 + 5 =
= 15 − 7
3
√
5 +
3
√
25
Funkcja
f : {
−3
,
−2
,
0
,
1
} → R
każdej liczbie ze zbioru
{
−3
,
−2
,
0
,
1
}
przyporządkowuje
jej kwadrat pomniejszony o
4
. Określ funkcję za pomocą grafu, tabelki, wzoru. Podaj zbiór
wartości funkcji.
Rozwiązanie:
Wzór tej
:
f (x) = x
2
− 4
tej funkcji dla
:
−3
,
−2
,
0
,
1
f (
−3
) = (
−3
)
2
− 4 = 9 − 4
f (
0
) =
0
2
− 4 = 0 − 4
f (
−3
) = 5
f (
0
) = −4
f (
−2
) = (
−2
)
2
− 4 = 4 − 4
f (
1
) =
1
2
− 4 = 1 − 4
—
1
f (
−2
) = 0
f (
1
) = −3
x
−3
−2
0
1
y
5
0
−4
−3
−3
5
−2
0
0
−4
1
−3
zbiór
funkcji:
{5, 0, −4, −3}
2
Narysuj wykres następującej funkcji.
y = 2x − 3
Rozwiązanie:
x
−1
0
2
y
−5
−3
1
x
y
Narysuj wykres następującej funkcji.
f (x) =
2
dla
x ∈ h−4, −2)
|x|
dla
x ∈ h−2, 2i
2x − 2
dla
x ∈ (2, ∞)
Rozwiązanie
:
y = 2
y = |x|
x
−4
−3
y
2
2
x
−2
0
2
y
2
0
2
y = 2x − 2
x
3
4
5
y
4
6
8
x
y
Narysuj wykres następującej funkcji.
y = 2|x|
Rozwiązanie
:
x
−2
−1
0
1
2
y
4
2
0
2
4
—
2
x
y
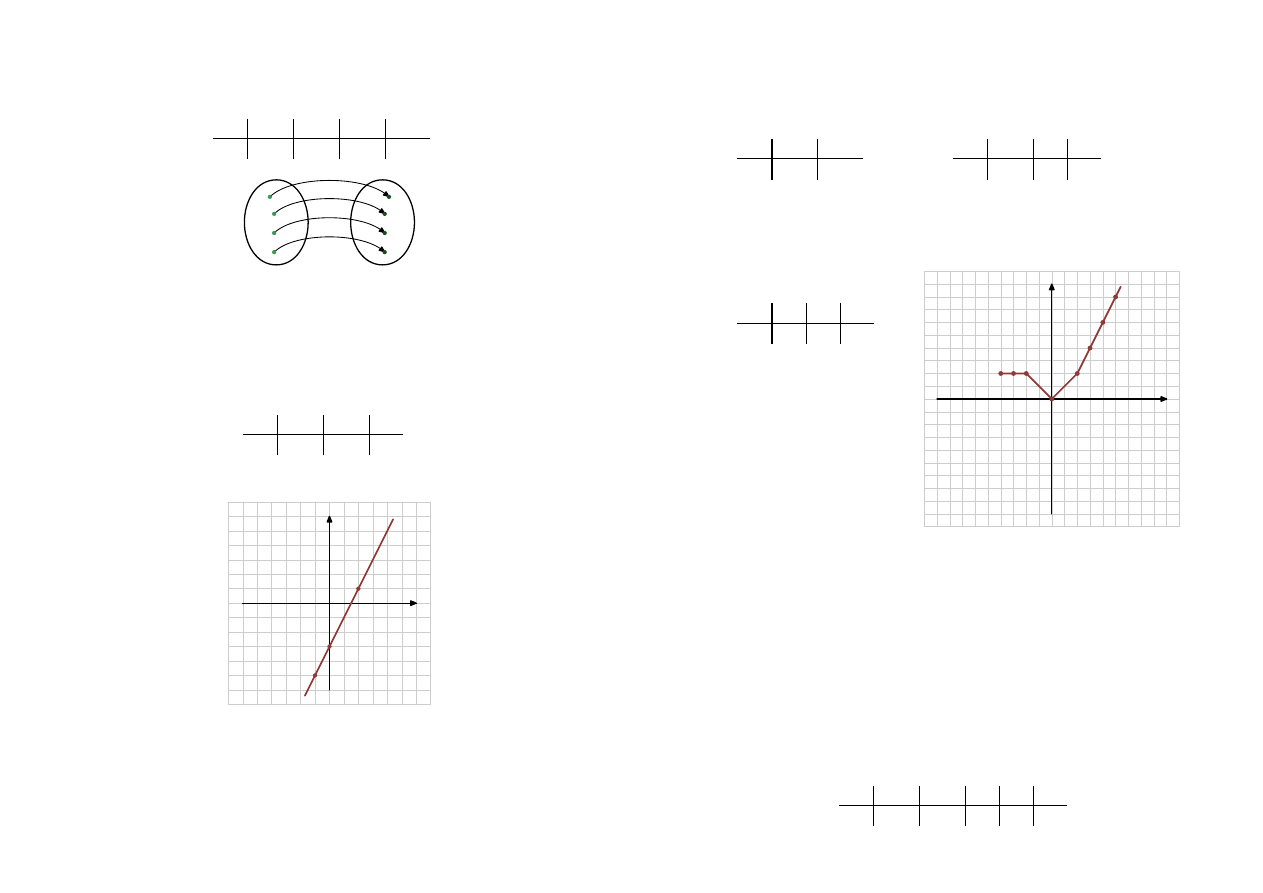
Narysuj wykres następującej funkcji.
f (x) =
−1
dla
x ∈ (−∞, −3) ∪ (3, ∞)
−|x| + 2
dla
x ∈ h−3, 3i
Rozwiązanie
:
y = −1
y = −|x| + 2
x
−6
−4
4
6
y
−1
−1
−1
−1
x
−3
−2
0
2
3
y
−1
0
2
0
−1
x
y
Dziedzina funkcji
Dziedzina
to zbiór zawierający wszystkie liczby, które możemy podstawić do wzoru funk-
cji. Możemy ją też odczytać z wykresu funkcji.
Oznaczenia:
D D
f
X
Przykłady:
y =
√
x
D = h0, ∞)
,
ponieważ nie można pierwiastkować liczb ujemnych.
y =
1
x
D = R \ {0}
, ponieważ nie można dzielić przez 0
(
1
x
= 1 : x).
-2
5
x
y
D = h−2, 5)
Znajdź dziedzinę funkcji.
f (x) =
√
3x + 9
Rozwiązanie
:
Wyznaczamy
wiedząc, że liczb ujemnych nie możemy pierwiastkować.
3x + 9 0
3x −9 / : 3
x −3
Odp.
D = h−3, ∞)
Znajdź dziedzinę funkcji.
f (x) =
√
4 − 2x
Rozwiązanie
:
Wyznaczamy
wiedząc, że liczb ujemnych nie możemy pierwiastkować.
4 − 2x 0
—
3
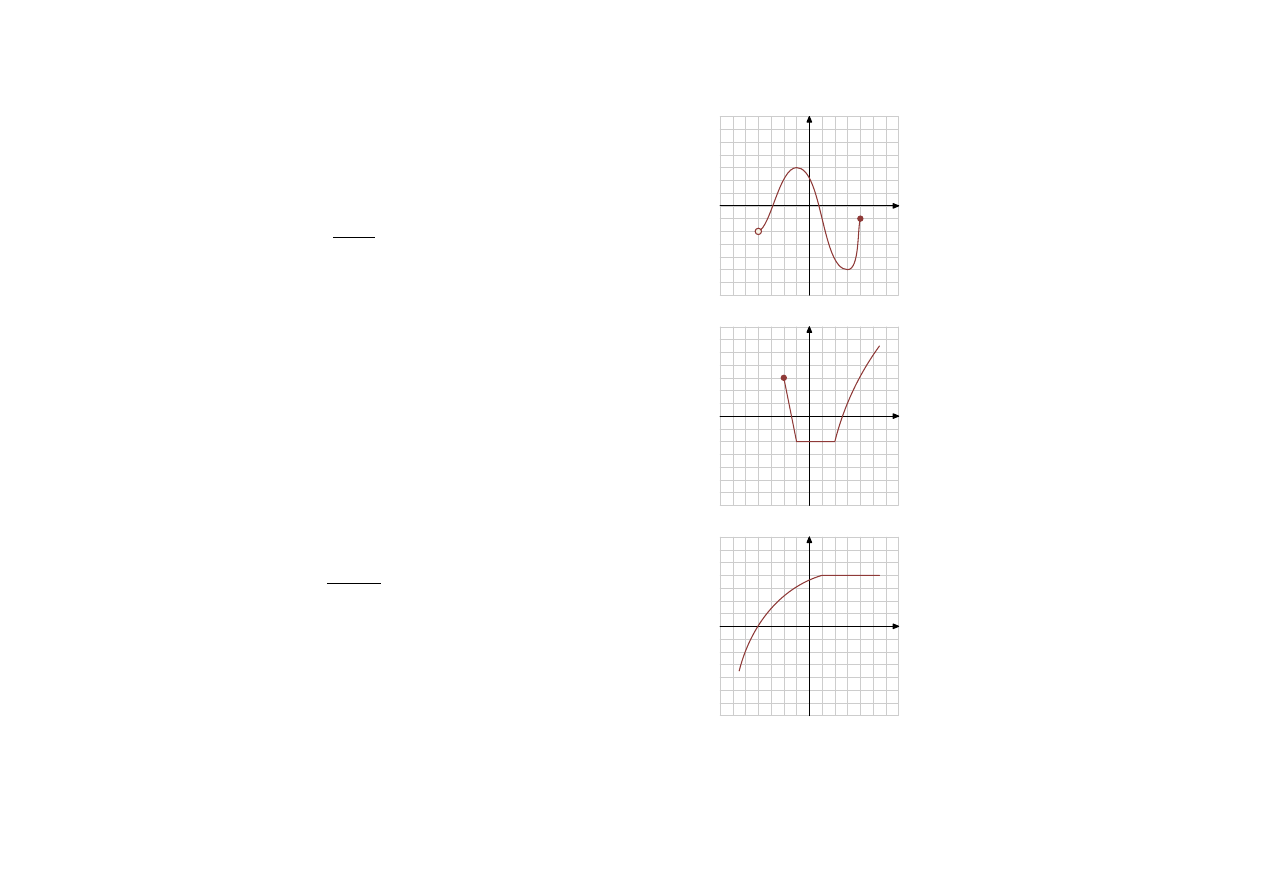
−2x −4 / : (−2)
x ¬ 2
Odp.
D = (−∞, 2i
Znajdź dziedzinę funkcji.
f (x) =
5
2x + 6
Rozwiązanie
:
Mianownik nie może być równy 0, ponieważ nie wolno dzielić przez 0.
2x + 6 = 0
2x = −6 / : 2
x = −3
Odp.
D = R \ {−3}
Znajdź dziedzinę funkcji.
f (x) =
4
x(x + 3)
Rozwiązanie:
Mianownik nie może być równy 0, ponieważ nie wolno dzielić przez 0.
x(x + 3) = 0
x = 0
lub
x + 3 = 0
x = −3
Odp.
D = R \ {0, −3}
Odczytaj dziedzinę funkcji o podanych wykresach.
Rozwiązanie
:
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
:
D = (−4, 4i
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
:
D = h−2, ∞)
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
:
D = R
Zbiór wartości
Zbiór wartości to zbiór zawierający wszystkie liczby, które możemy otrzymać ze wzoru
.
—
4
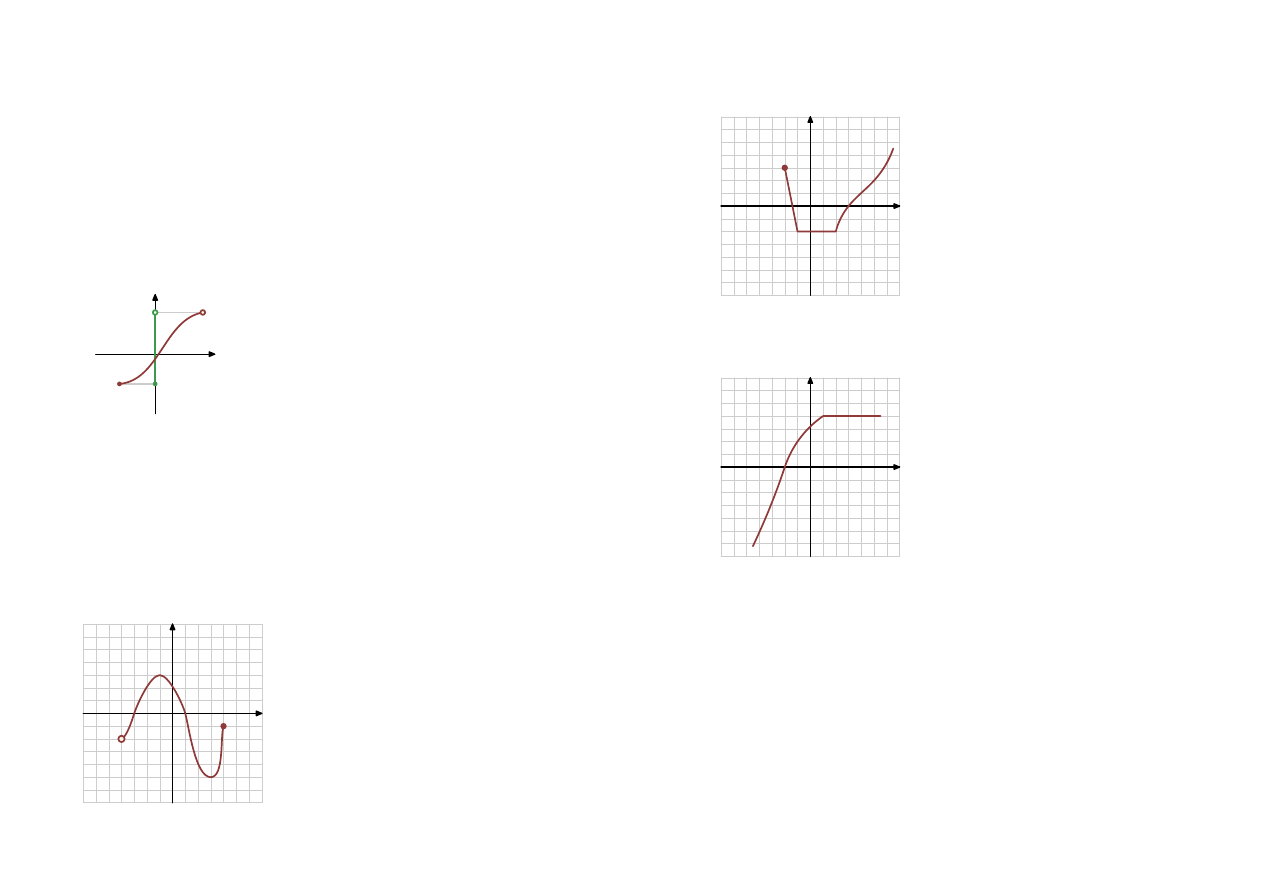
Możemy go też odczytać z wykresu funkcji.
Oznaczenia:
ZW, ZW
f
, Z
f
, Y
Przykłady:
y = x
2
ZW = h0, ∞)
, ponieważ podnosząc do kwadratu
otrzymujemy liczby nieujemne.
y = x + 1
ZW = R
,
ponieważ możemy otrzymać dowolną liczbę
wstawiając odpowiednią za
x
.
-2
4
x
y
ZW = h−2, 4)
Odczytaj z wykresów funkcji dla jakich
,
funkcji wynoszą
−5
,
0
,
2
Rozwiązanie
:
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
f (3) =
−5
f (−3) =
0
f (1) =
0
f (−2) =
2
f (0) =
2
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
funkcja dla żadnego argumentu
nie przyjmuje wartości
−5
f (−1, 5) =
0
f (3) =
0
f (−1, 8) =
2
f (5) =
2
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
f (−4) =
−5
f (−2) =
0
f (−1) =
2
Miejsce zerowe
Miejsce zerowe to liczba, która podstawiona do wzoru
daje wartość równą 0. Miejsce
zerowe możemy też odczytać z wykresu funkcji.
Przykłady:
y = x + 2
x
0
= −2
, ponieważ podstawiając
−2
za
x
otrzymujemy 0.
y = 2x − 6
x
0
= 3
,
ponieważ podstawiając 3 za
x
otrzymujemy 0.
—
5
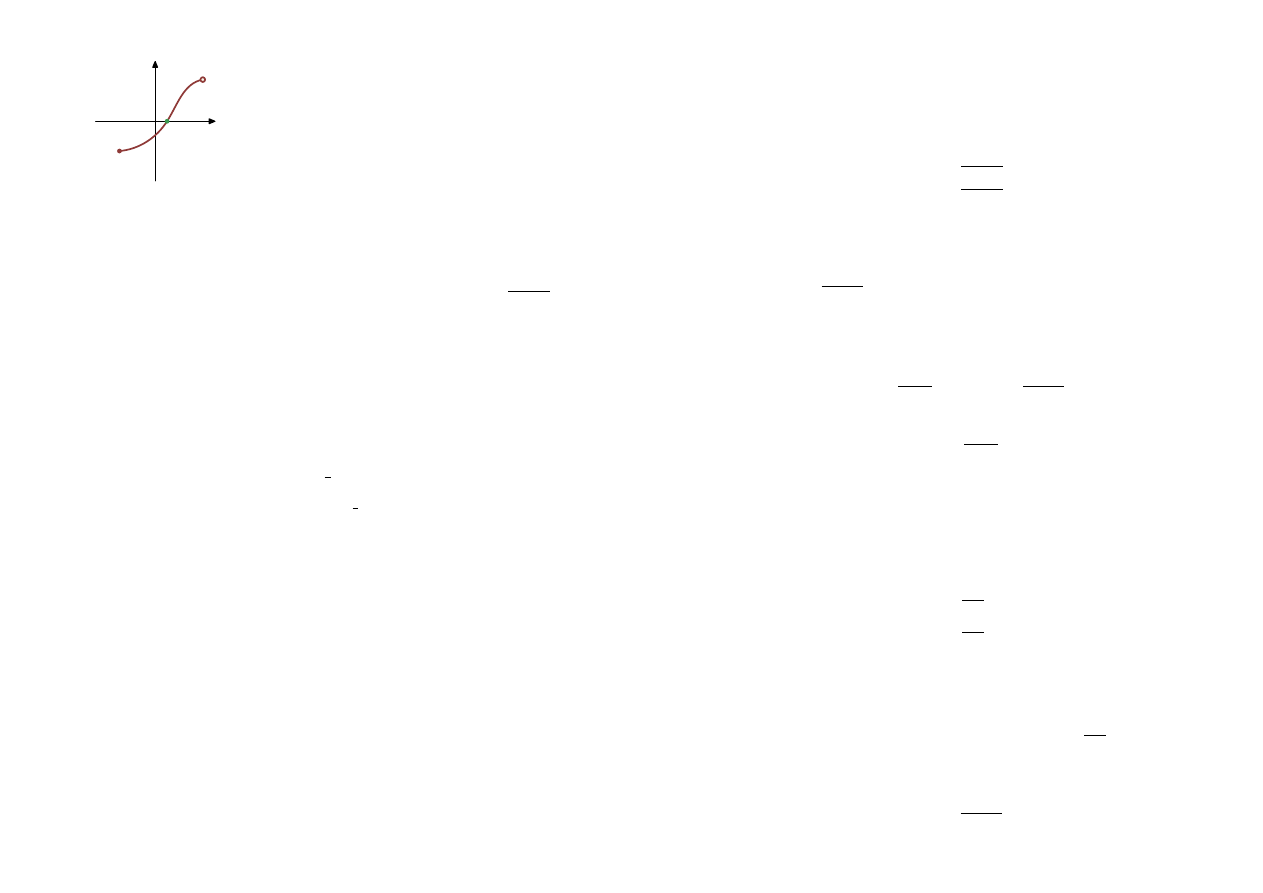
1
x
y
x
0
= 1
Oblicz miejsze zerowe funkcji.
y = 3x − 2
y = x
2
− 4
y = x
2
− 2x
y =
√
2x − 6
Rozwiązanie
:
Wyznaczając
szukam dla jakiego
x
mam
y = 0
.
y = 3x − 2
0 = 3x − 2
2 = 3x
3x = 2
: 3
x =
2
3
Odp.
funkcji
y = 3x − 2
to
x
0
=
2
3
.
y = x
2
− 4
0 = x
2
− 4
4 = x
2
x
2
= 4
x
1
= −2
i
x
2
= 2
Odp. Funkcja
y = x
2
− 4
ma dwa
x
1
= −2
i
x
2
= 2
.
y = x
2
− 2x
0 = x
2
− 2x
0 = x(x − 2)
x(x − 2) = 0
x
1
= 0
i
x
2
= 2
Odp. Funkcja
y = x
2
− 2x
ma dwa
:
x
1
= 0
i
x
2
= 2
.
y =
√
2x − 6
0 =
√
2x − 6
0 = 2x − 6
−2x = −6
: (−2)
x
0
= 3
Odp. Funkcja
y =
√
2x − 6
ma jedno
x
0
= 3
.
Oblicz miejsce zerowe funkcji.
y =
3x
x + 2
y =
x
2
− 6
x
2
+ 3
Rozwiązanie
:
y =
3x
x + 2
Na początku szukam
tej funkcji.
x + 2 = 0
x = −2
Mianownik nie może być równa
0
, a tak jest dla
x = −2
, dlatego dziedzina funkcji to
x ∈
R \ {−2}
. Wyznaczając
szukam dla jakiego
x
mam
y = 0
.
y =
3x
x+2
0 =
3x
x+2
0 = 3x
3x = 0
: 3
x
0
=
0
Odp.
Wynik
0
należy
do
dziedziny
funkcji.
Funkcja
y =
3x
x+2
ma
jedno
miejsce
zerowe:
x
0
=
0
.
y =
x
2
− 6
x
2
+ 3
—
6
Na początku szukam
tej funkcji.
x
2
+ 3 = 0
x
2
= −3
To równanie nia ma rozwiązania, dlatego dziedzina funkcji są wszystkie liczby rzeczywiste.
Wyznaczając
szukam dla jakiego
x
mam
y = 0
.
y =
x
2
−6
x
2
+3
0 =
x
2
−6
x
2
+3
0 = x
2
− 6
6 = x
2
x
2
= 6
x
1
=
√
6
i
x
2
=
−
√
6
Odp. Funkcja
y =
x
2
−6
x
2
+3
ma dwa miejsca zerowe:
x
1
=
√
6
i
x
2
=
−
√
6
.
Wyznacz miejsca zerowe funkcji o podanych wykresach.
Rozwiązanie
:
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
x
1
= −3
,
x
2
= 1
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
x
1
= −1, 5
;
x
2
= 3
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
x
1
= −2
Monotoniczność
Monotoniczność oznacza najczęściej, że
jest rosnąca, malejąca lub stała.
Funkcja
Definicja funkcji rosnącej:
rosnąca:
Dla każdego
x
1
< x
2
:
f (x
1
) < f (x
2
)
x
y
x
1
x
2
f (x
1
)
f (x
2
)
—
7
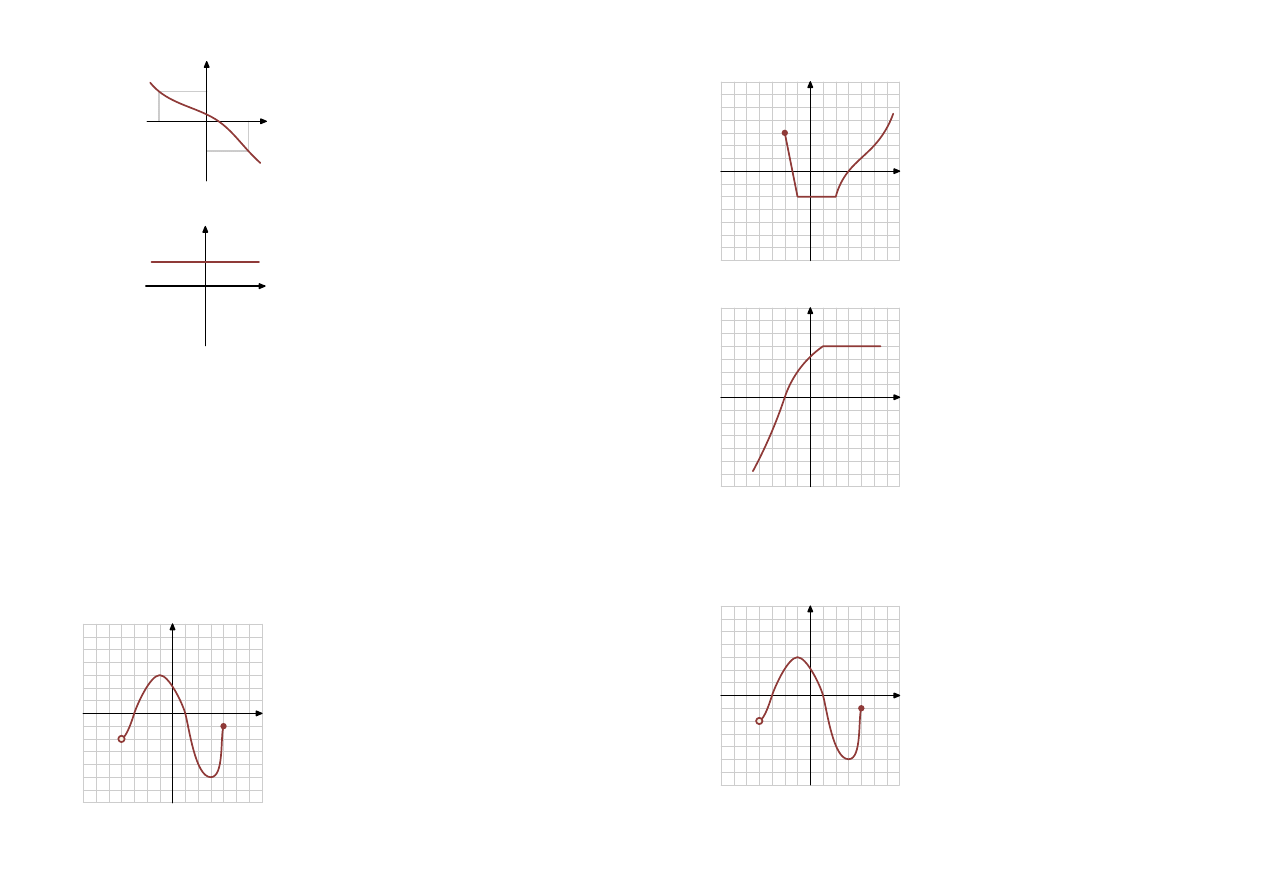
Funkcja
Definicja funkcji malejącej:
malejąca:
Dla każdego
x
1
< x
2
:
f (x
1
) > f (x
2
)
x
y
x
2
x
1
f (x
2
)
f (x
1
)
Funkcja
Definicja funkcji stałej:
stała:
Dla każdego
x
:
f (x) = c
x
y
c
Wyznacz przedziały
dla funkcji o podanych wykresach.
Rozwiązanie
:
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
funkcja jest:
dla
x ∈ (−4, −1i
dla
x ∈ h−1, 3i
rosnąca dla
x ∈ h3, 4i
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
funkcja jest:
malejąca dla
x ∈ h−2, −1i
dla
x ∈ h−1, 2i
rosnąca dla
x ∈ h2, ∞)
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
funkcja jest:
rosnąca dla
x ∈ (−∞, 1i
stała dla
x ∈ h1, ∞)
Odczytaj z wykresu najmniejszą i największą
funkcji.
Rozwiązanie
:
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
Największa wartość:
y
max
= 3
Minimalna wartość:
y
min
= −5
—
8
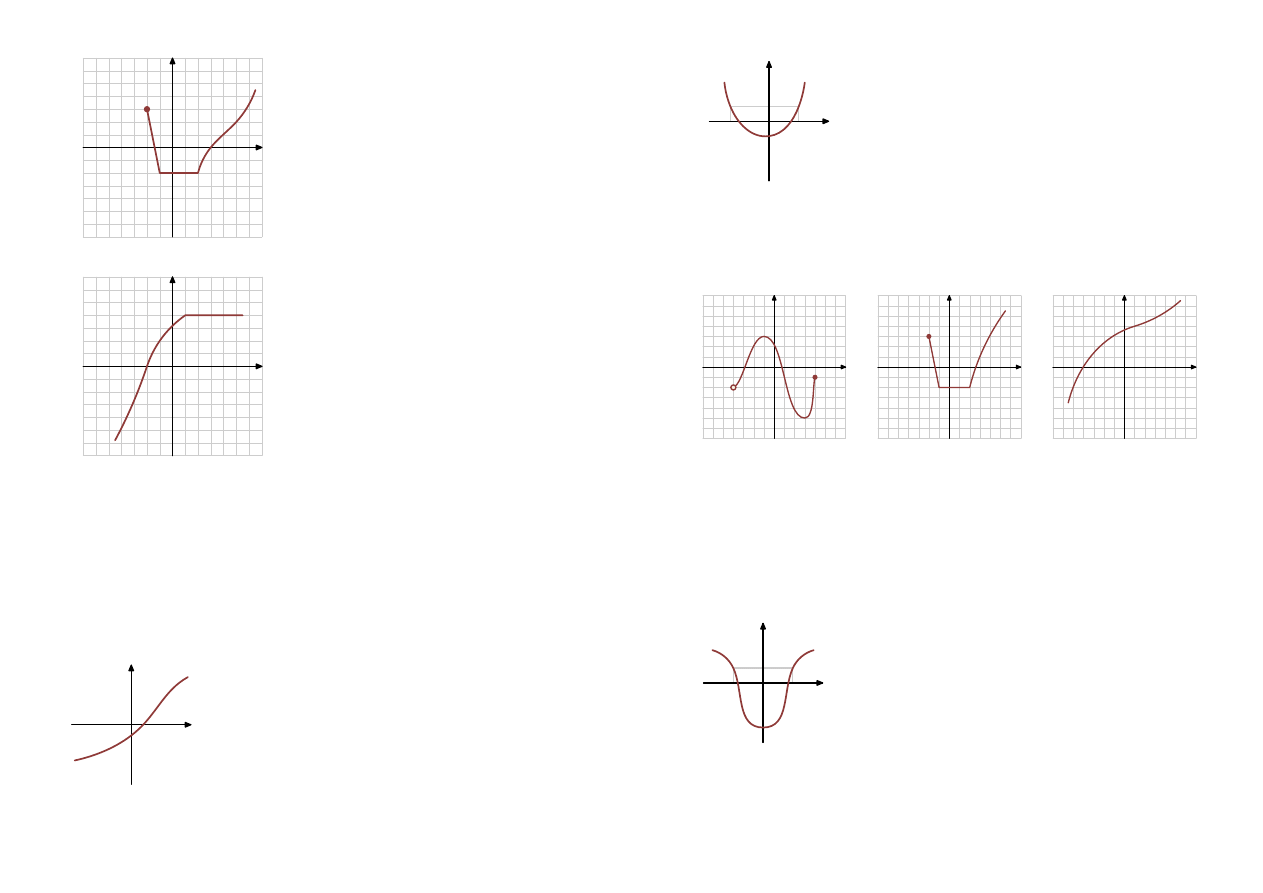
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
Funkcja nie ma największa wartości.
Najmniejsza wartość:
y
min
= −2
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
Maksymalna wartość:
y
max
= 4
Funkcja nie ma najmniejszej wartości.
Różnowartościowość
Funkcja jest różnowartościowa, jeżeli nie ma takich dwóch liczb, dla których
funkcji
wynosi tyle samo.
Przykłady:
x
y
funkcja różnowartościowa
x
y
-4
3
1
funkcja nie jest różnowartościowa, ponieważ
dla
−4
i 3 wartość wynosi tyle samo.
Czy funkcje o podanych wykresach są różnowartościowe?
Rozwiązanie
:
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
x
y
1 2 3 4 5
−1
−2
−3
−4
−5
1
2
3
4
5
−1
−2
−3
−4
−5
funkcja
nie jest
funkcja
nie jest
funkcja
jest
Parzystość i nieparzystość
Funkcja jest
parzysta
, jeżeli dla dowolnych liczb przeciwnych
funkcji wynosi tyle samo.
Lewa strona wykresu jest odbiciem prawej.
f (−x) = f (x)
Funkcja parzysta, ponieważ dla liczb przeciwnych
(np
−3
,
3
) wartość wynosi tyle samo.
Przykłady funkcji parzystych:
x
y
-3
3
2
Funkcja jest
nieparzysta
, jeżeli dla dowolnych liczb przeciwnych wartości funkcji są też przeciwne.
—
9
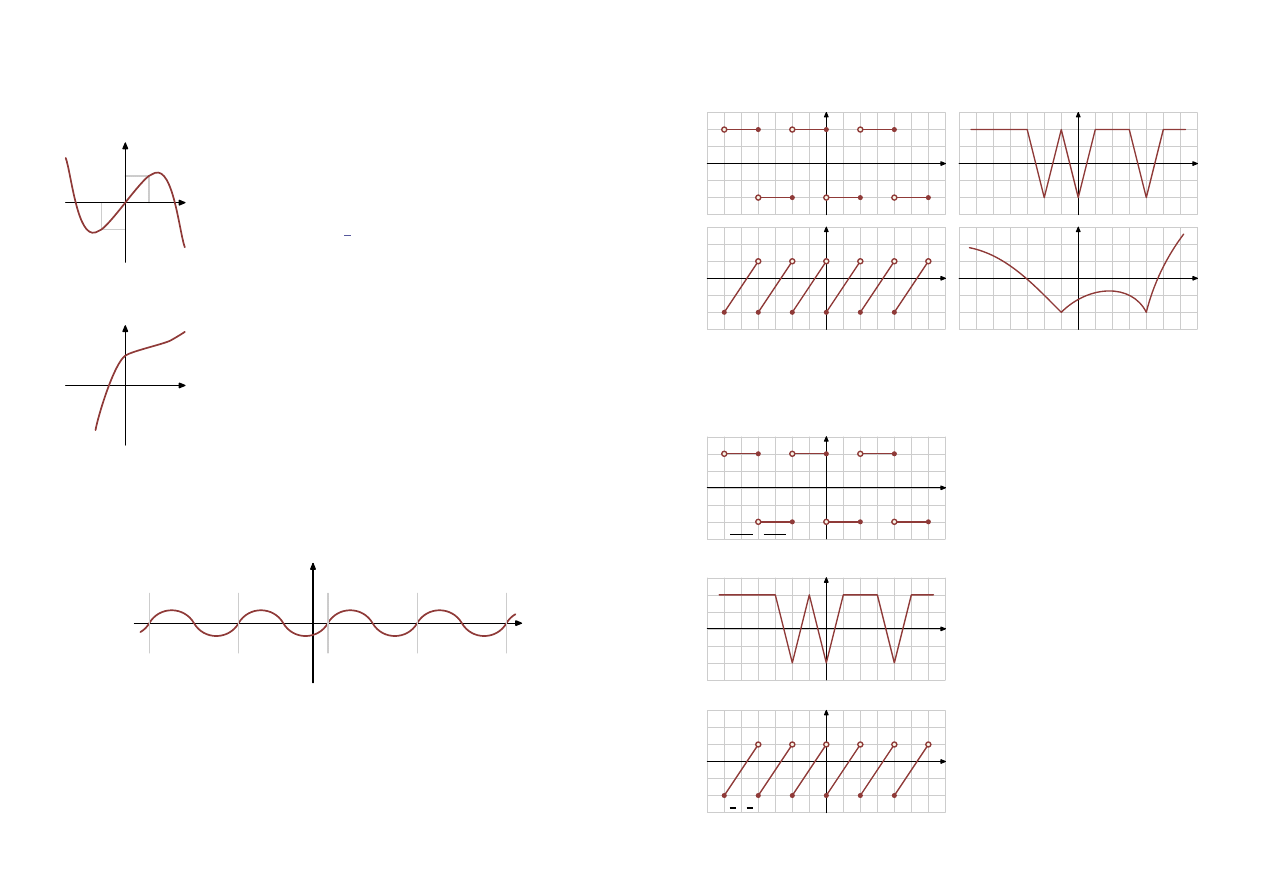
Lewa strona wykresu jest odwróconym odbiciem prawej.
f (−x) = −f (x)
Funkcja nieparzysta, ponieważ dla liczb przeciwnych
(np
−5
,
5
) wartości też są przeciwne.
Przykłady funkcji nieparzystych:
x
y
-5
5
-4
4
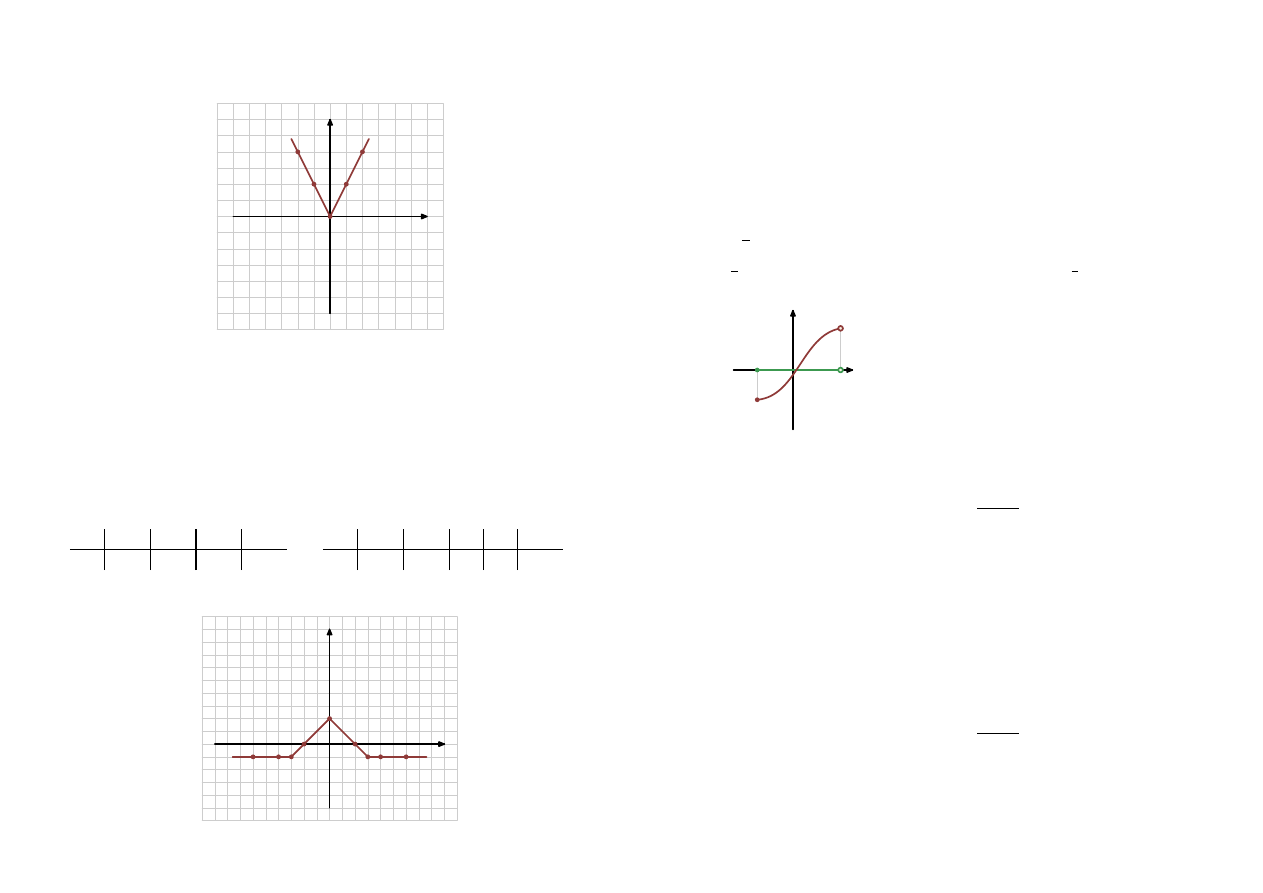
Funkcja nie jest ani
parzysta
, ani
nieparzysta
.
Tak jest z większością funkcji.
x
y
Okresowość funkcji
Funkcja jest okresowa, jeżeli jej wykres da się podzielić na nieskończenie wiele identycznych
części.
x
y
Okres funkcji - długość jednej części na jakie został podzielony wykres.
Przykłady funkcji okresowych:
Zadania + Rozwiązania
Wskaż wykresy funkcji okresowych i wartość ich okresu podstawowego.
x
y
1
x
y
1
x
y
1
x
y
1
Wskaż wykresy funkcji okresowych i wartość ich okresu podstawowego.
Rozwiązanie
:
x
y
1
|
{z
}
T = 4
Okres podstawowy:
T = 4
x
y
1
Funkcja nie jest okresowa.
x
y
1
|
{z
}
T = 2
Okres podstawowy:
T = 2
—
10
—
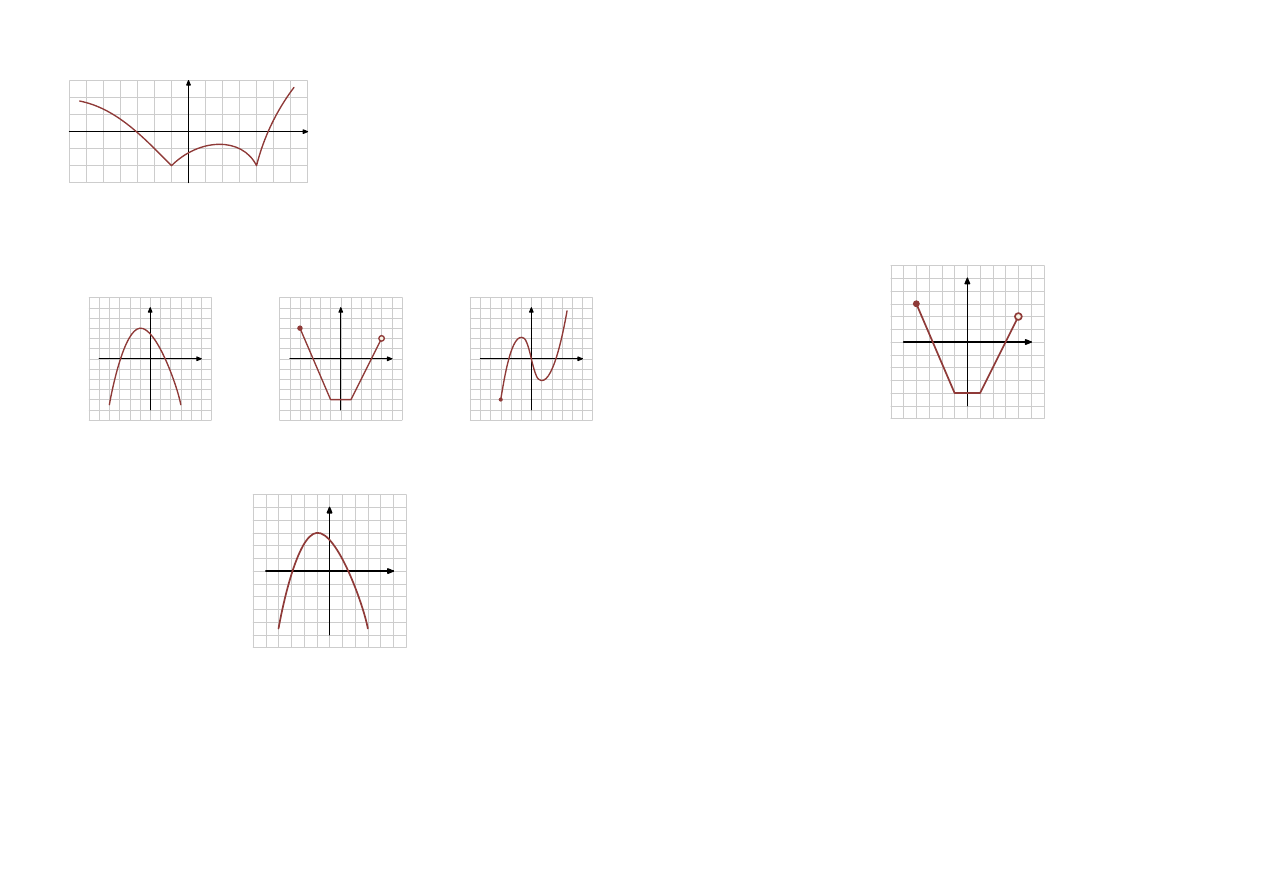
x
y
1
Funkcja nie jest okresowa.
Zadania + Rozwiązania
Dla poniższych funkcji określ dziedzinę, zbiór wartości, miejsca zerowe, monotoniczność, różno-
wartościowość, parzystość, okresowość.
x
y
1
x
y
1
x
y
1
Dla poniższej funkcji określ dziedzinę, zbiór wartości, miejsca zerowe, monotoniczność, różno-
wartościowość, parzystość, okresowość.
x
y
1
Rozwiązanie
:
D = R
:
ZW = (−∞, 3i
:
x
0
≈ −3
lub
x
0
≈ 1, 5
:
funkcja jest przedziałami monotoniczna
rosnąca w przedziale
(−∞, −1i
malejąca w przedziale
h−1, ∞)
funkcja nie jest różnowartościowa
:
funkcja nie jest ani parzysta ani nieparzysta
funkcja nie jest okresowa
Dla poniższej funkcji określ dziedzinę, zbiór wartości, miejsca zerowe, monotoniczność, różno-
wartościowość, parzystość, okresowość.
x
y
1
Rozwiązanie
:
D = h−4, 4)
ZW = h−4, 3i
:
x
0
≈ −2,8
lub
x
0
= 3
:
funkcja jest przedziałami monotoniczna
malejąca w przedziale
h−4, −1i
stała w przedziale
h−1, 1i
rosnąca w przedziale
h1, 4)
funkcja nie jest różnowartościowa
:
funkcja nie jest ani parzysta ani nieparzysta
funkcja nie jest okresowa
Dla poniższej funkcji określ dziedzinę, zbiór wartości, miejsca zerowe, monotoniczność, różno-
—
11
—
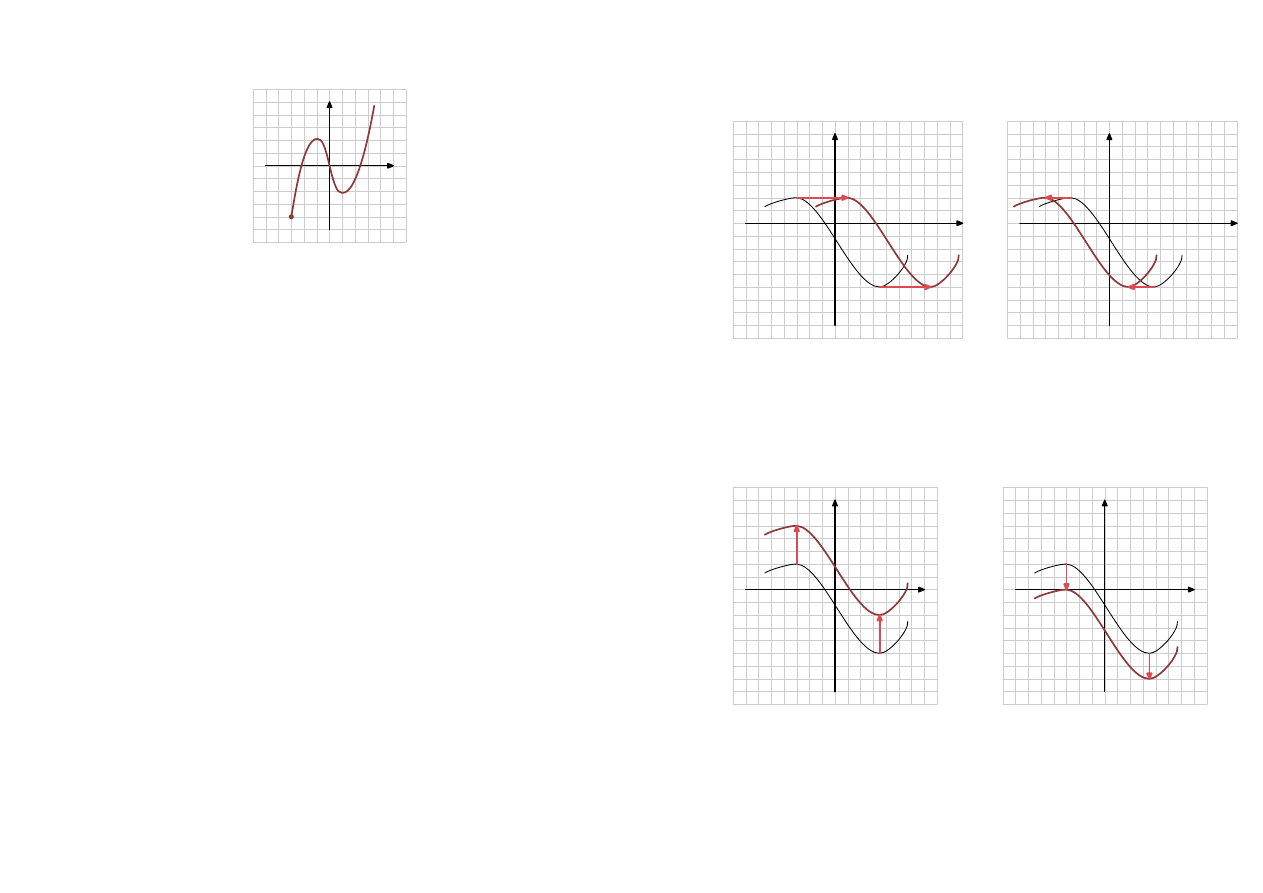
wartościowość, parzystość, okresowość.
x
y
1
Rozwiązanie
:
D = h−3, ∞)
:
ZW = h−4, ∞)
:
x
0
≈ −2, 1
lub
x
0
= 0
lub
x
0
≈ 2, 3
:
funkcja jest przedziałami monotoniczna
rosnąca w przedziale
h−3, −1i
malejąca w przedziale
h−1, 1i
rosnąca w przedziale
h1, ∞)
funkcja nie jest różnowartościowa
funkcja nie jest ani parzysta ani nieparzysta
:
funkcja nie jest okresowa
Przesunięcie wykresu wzdłuż osi
x
Wykres funkcji
f (x − a)
otrzymuję przez przesunięcie wykresu
f (x)
o
a
w prawo.
Wykres funkcji
f (x + a)
otrzymuję przez przesunięcie wykresu
f (x)
o
a
w lewo.
Przykłady
:
x
y
1
1
f (x)
f (x − 4)
x
y
1
1
f (x)
f (x + 2)
Przesunięcie wykresu wzdłuż osi
y
Wykres funkcji
f (x) + b
otrzymuję przez przesunięcie wykresu
f (x)
o
b
do góry.
Wykres funkcji
f (x) − b
otrzymuję przez przesunięcie wykresu
f (x)
o
b
do dołu.
Przykłady
:
x
y
1
1
f (x)
f (x) + 3
x
y
1
1
f (x)
f (x) − 2
Narysuj wykres funkcji
y = x
2
a następnie przekształć go tak aby otrzymać wykres funkcji
—
12
—
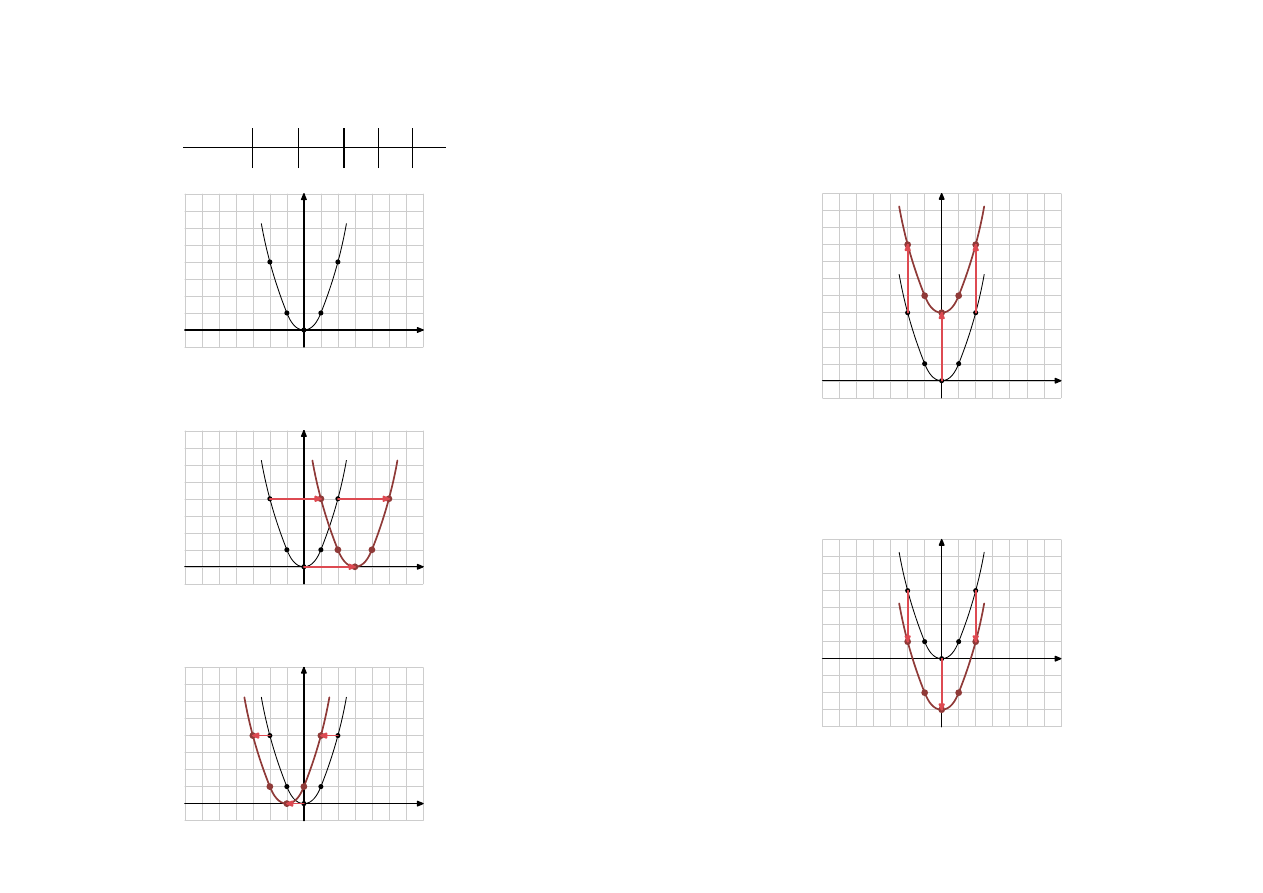
y = (x − 3)
2
,
y = (x + 1)
2
,
y = x
2
+ 4
,
y = x
2
− 3
.
Rozwiązanie
:
x
−2
−1
0
1
2
y = x
2
4
1
0
1
4
x
y
Wykres
y = (x − 3)
2
otrzymuję przesuwając
y = x
2
o
3
w prawo.
x
y
Wykres
y = (x + 1)
2
= (x − (−1))
2
otrzymuję przesuwając
y = x
2
o
1
w lewo.
x
y
Wykres
y = x
2
+ 4
otrzymuję przesuwając
y = x
2
o
4
w górę.
x
y
Wykres
y = x
2
− 3
otrzymuję przesuwając
y = x
2
o
3
w dół.
x
y
—
13
—
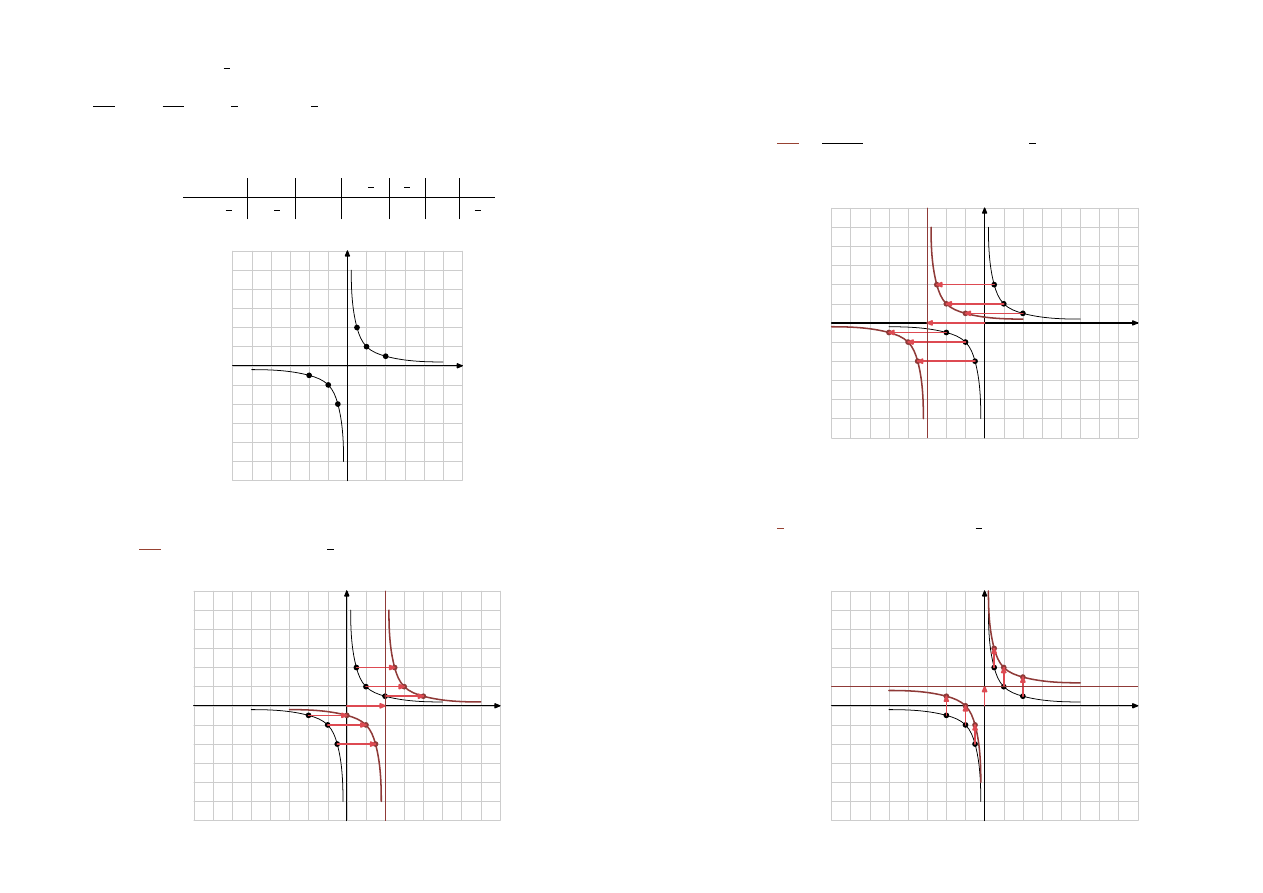
Narysuj wykres funkcji
y =
1
x
a następnie przekształć go tak aby otrzymać wykres funkcji:
y =
1
x−2
,
y =
1
x+3
,
y =
1
x
+ 1
,
y =
1
x
− 1
.
Rozwiązanie
:
x
−2
−1
−
1
2
1
2
1
2
y =
1
x
−
1
2
−1
−2
2
1
1
2
x
y
1
1
Wykres
y =
1
x−2
otrzymuję przesuwając
y =
1
x
o
2
w prawo.
x
y
1
1
Wykres
y =
1
x+3
=
1
x−(−3)
otrzymuję przesuwając
y =
1
x
o
3
w lewo.
x
y
1
1
Wykres
y =
1
x
+ 1
otrzymuję przesuwając
y =
1
x
o
1
w górę.
x
y
1
1
—
14
—
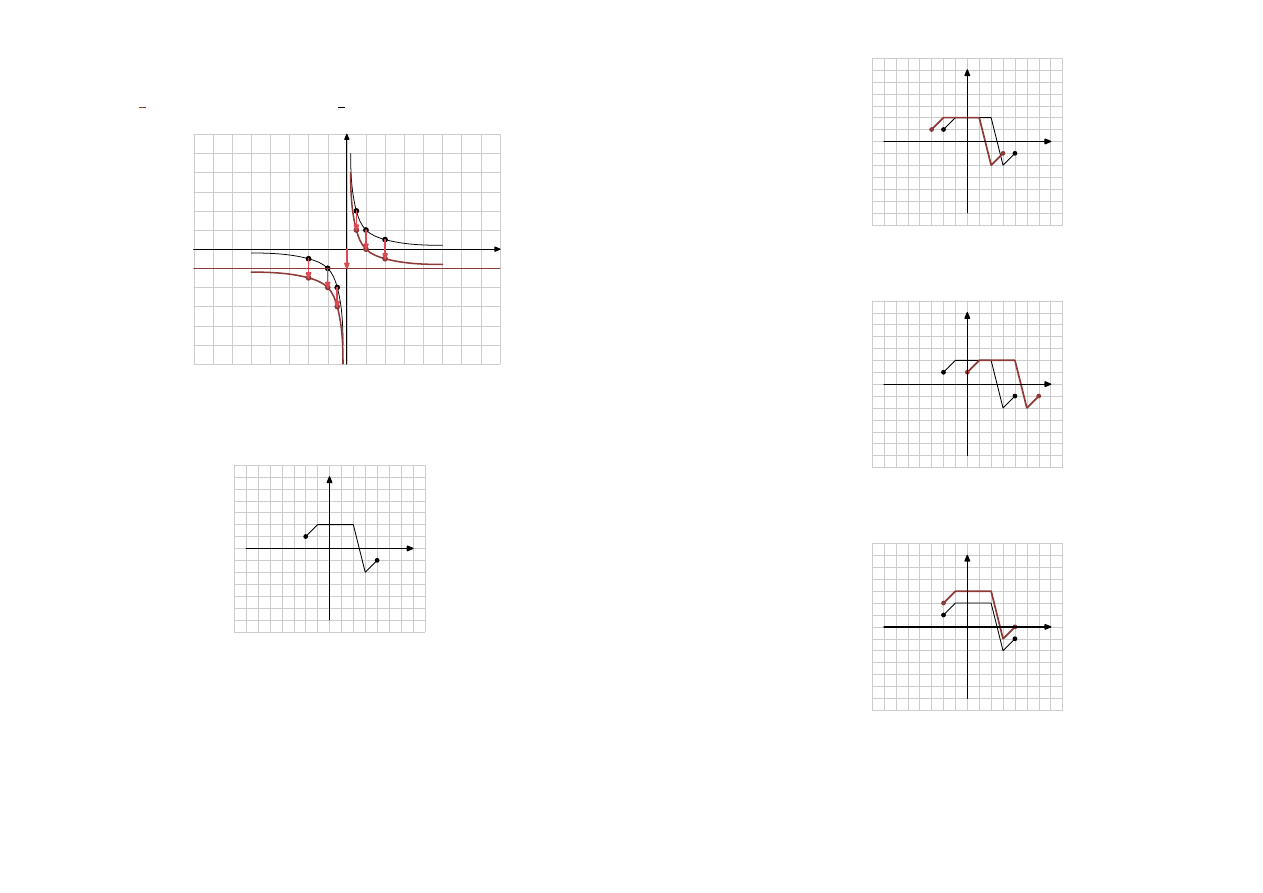
Wykres
y =
1
x
− 1
otrzymuję przesuwając
y =
1
x
o
1
w dół.
x
y
1
Rysunek przedstawia wykres funkcji
y = f (x)
.
x
y
1
1
y = f (x)
Narysuj wykresy funkcji:
y = f (x + 1)
,
y = f (x) + 1
,
y = f (x + 2) − 1
,
y = f (x − 1) + 1
.
y = f (x − 2)
,
y = f (x) − 3
,
y = f (x − 3) − 2
,
Rozwiązanie
:
Wykres
y = f (x +
1
)
otrzymuję przesuwając wykres
y = f (x)
o
1
w lewo.
x
y
1
1
y = f (x)
y = f (x + 1)
Wykres
y = f (x −
2
)
otrzymuję przesuwając wykres
y = f (x)
o
2
w prawo.
x
y
1
1
y = f (x)
y = f (x − 2)
Wykres
y = f (x) +
1
otrzymuję przesuwając wykres
y = f (x)
o
1
do góry.
x
y
1
1
y = f (x)
y = f (x) + 1
Wykres
y = f (x) −
3
otrzymuję przesuwając wykres
y = f (x)
o
3
do dołu.
—
15
—
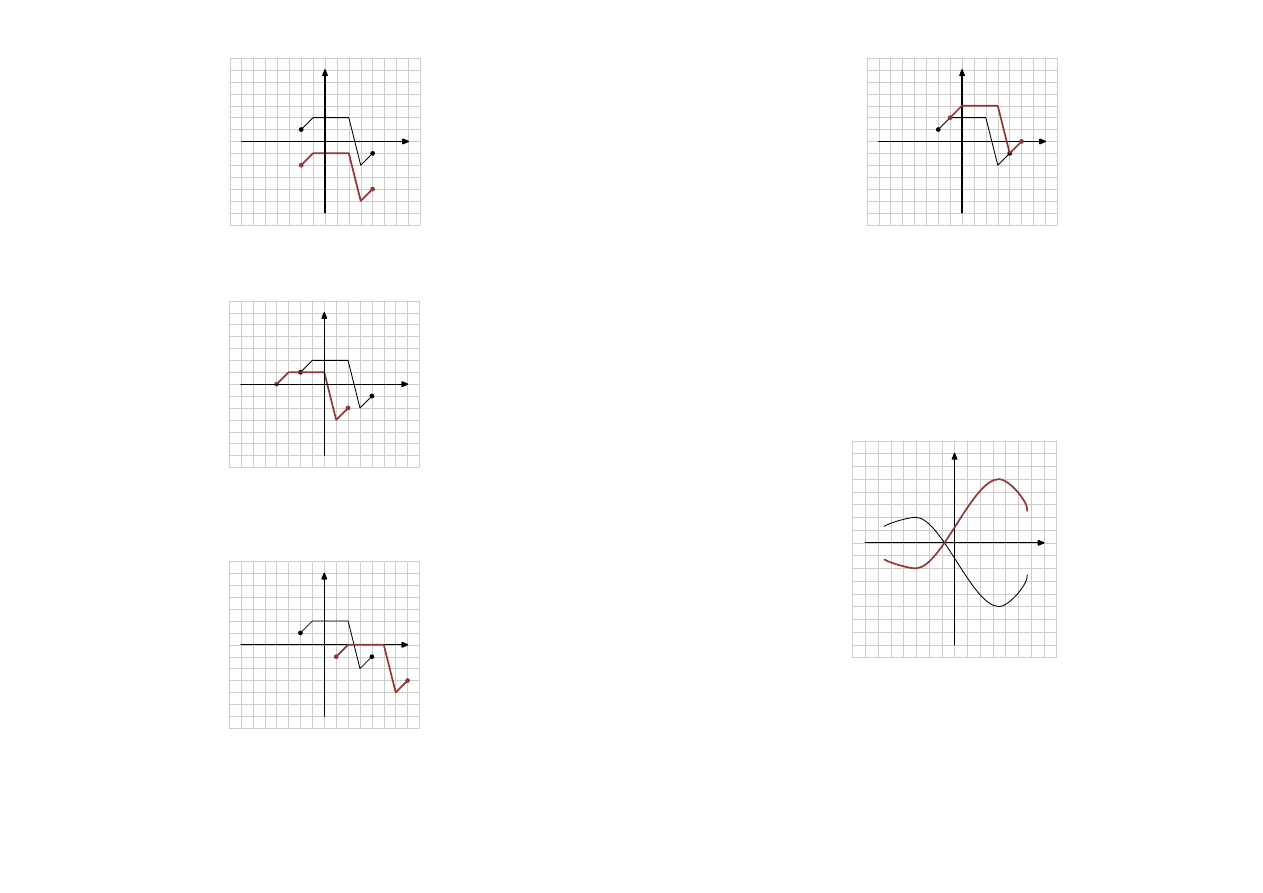
x
y
1
1
y = f (x)
y = f (x) − 3
Wykres
y = f (x+
2
)−
1
otrzymuję przesuwając wykres
y = f (x)
o
2
w lewo i
1
do dołu.
x
y
1
1
y = f (x)
y = f (x + 2) − 1
Wykres
y = f (x −
3
) −
2
otrzymuję przesuwając wykres
y = f (x)
o
3
w prawo i
2
do
dołu.
x
y
1
1
y = f (x)
y = f (x − 3) − 2
Wykres
y = f (x −
1
) +
1
otrzymuję przesuwając wykres
y = f (x)
o
1
w prawo i
1
do
góry.
x
y
1
1
y = f (x)
y = f (x − 1) + 1
Odbicie wykresu względem osi
x
Wykres funkcji
−f (x)
otrzymuję przez odbicie
f (x)
względem osi
x
. Wykresy
f (x)
i
−f (x)
są
względem osi
x
.
x
y
1
1
f (x)
−f (x)
Odbicie wykresu względem osi
y
Wykres funkcji
f (−x)
otrzymuję przez odbicie
f (x)
względem osi
y
. Wykresy
f (x)
i
f (−x)
są
względem osi
y
.
—
16
—
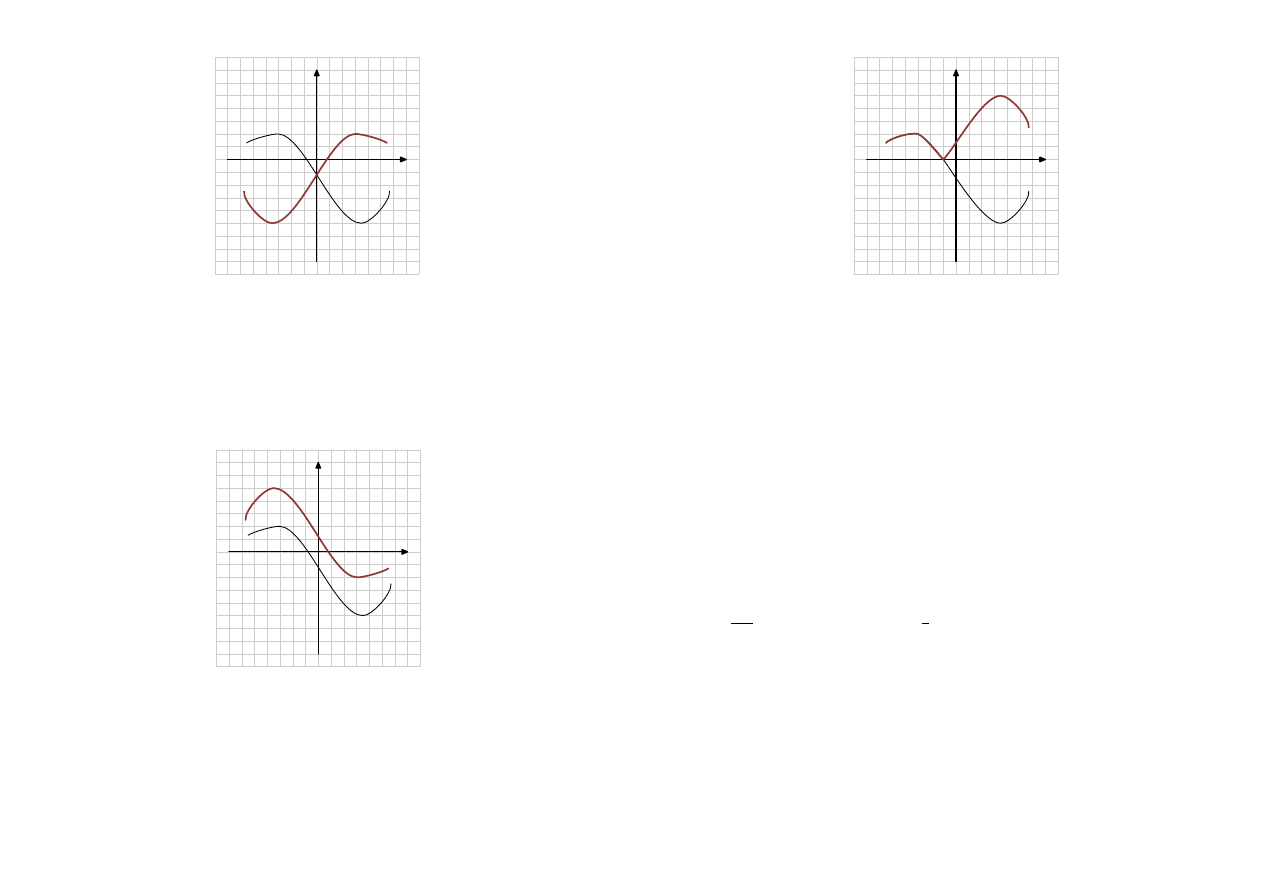
x
y
1
1
f (x)
f (−x)
Odbicie wykresu względem początku układu współrzędnych
Wykres funkcji
−f (−x)
otrzymuję przez odbicie
f (x)
względem początku układu współrzęd-
nych. Wykresy
f (x)
i
−f (−x)
są
symetryczne względem początku układu współrzędnych
.
x
y
1
1
f (x)
−f (−x)
Wykres wartości bezwzględnej z funkcji.
Wykres funkcji
|f (x)|
otrzymuję przez odbicie części wykresu
f (x)
znajdującej się pod osią
x
.
x
y
1
1
f (x)
|f (x)|
Przesuwanie wykresu funkcji
Wykres funkcji
f (x − a) + b
otrzymujemy przez narysowanie funkcji
f (x)
i przesunięciu jej o
[a, b]
.
Przykłady:
y = |x −
3
| +
2
rysujemy
y = |x|
i przesuwamy o wektor
[
3
,
2
]
y = (x −
2
)
2
−4
y = x
2
[
2
,
−4
]
y = (x +
1
)
3
+
2
y = x
3
[
−1
,
2
]
y = (x +
5
)
2
−3
y = x
2
[
−5
,
−3
]
y = x
2
+
1
y = x
2
[0,
1
]
y = (x −
2
)
2
y = x
2
[
2
, 0]
y =
2
x+
3
−1
y =
2
x
[
−3
,
−1
]
Pierwsza
współrzędna wektora ma przeciwny znak niż liczba przy
x
,
druga
współrzędna ma
znak taki sam jak liczba na końcu.
Narysuj wykres funkcji
y = |x − 3| + 2
—
17
—

Rozwiązanie
:
Wykres
y = |x −
3
| +
2
otrzymuję przesuwając
y = |x|
o
[
3
,
2
]
.
x
−2
−1
0
1
2
y = |x|
2
1
0
1
2
y = |x|
y = |x − 3| + 2
x
y
Narysuj wykres funkcji
y = |x + 1| − 2
Rozwiązanie
:
Wykres
y = |x +
1
|
−2
otrzymuję przesuwając
y = |x|
o
[
−1
,
−2
]
.
x
−2
−1
0
1
2
y = |x|
2
1
0
1
2
y = |x|
y = |x + 1| − 2
x
y
Narysuj wykres funkcji
y = (x − 2)
2
− 1
Rozwiązanie
:
Wykres
y = (x −
2
)
2
−1
otrzymuję przesuwając
y = x
2
o
[
2
,
−1
]
.
x
−2
−1
0
1
2
y = x
2
4
1
0
1
4
x
y
—
18
—
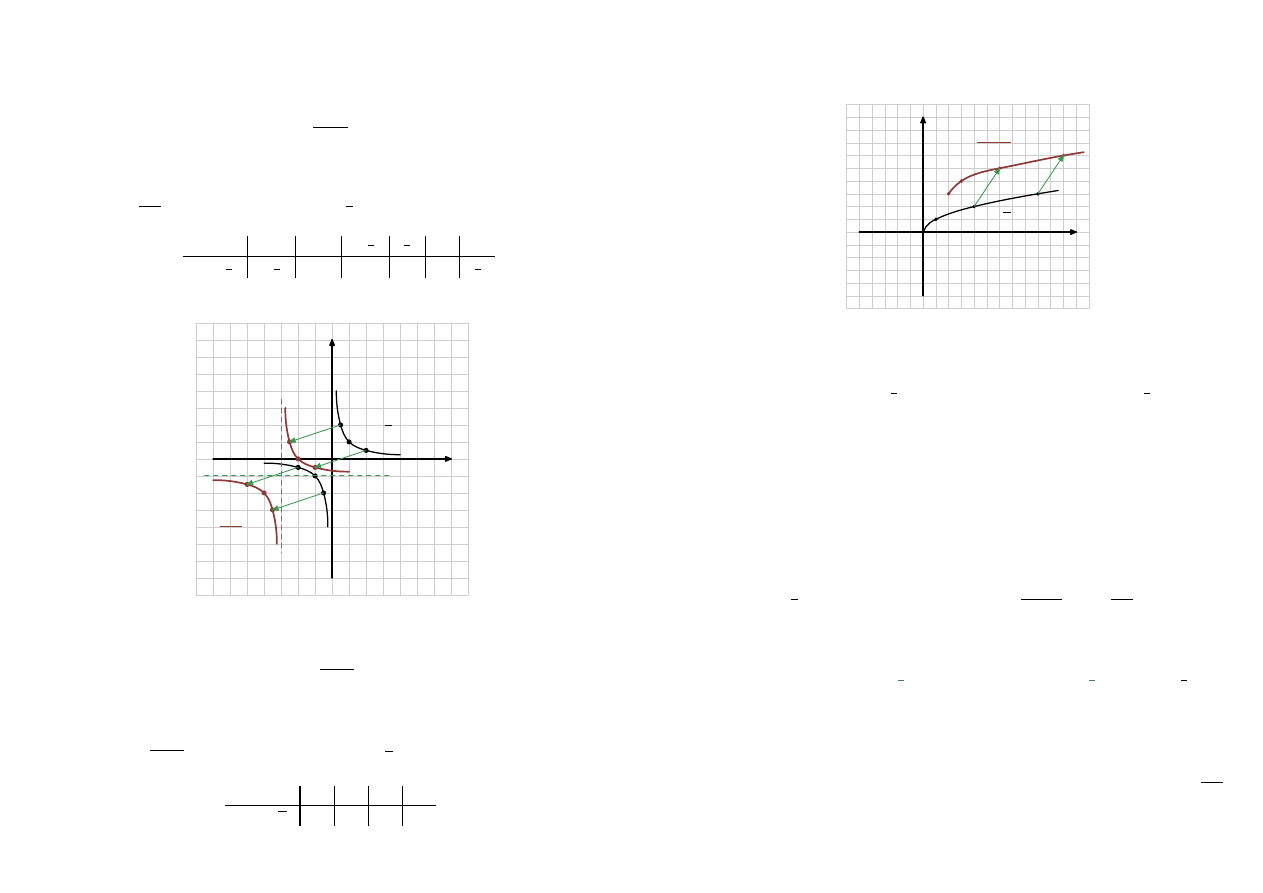
Narysuj wykres funkcji
y =
1
x + 3
− 1
Rozwiązanie
:
Wykres
y =
1
x+
3
−1
otrzymuję przesuwając
y =
1
x
o
[
−3
,
−1
]
.
x
−2
−1
−
1
2
1
2
1
2
y =
1
x
−
1
2
−1
−2
2
1
1
2
y =
1
x
y =
1
x+3
− 1
x
y
Narysuj wykres następującej funkcji.
y =
√
x − 2 + 3
Rozwiązanie
:
Wykres
y =
√
x −
2
+
3
otrzymuję przesuwając
y =
√
x
o
[
2
,
3
]
.
x
0
1
4
9
y =
√
x
0
1
2
3
x
y
y =
√
x
y =
√
x − 2 + 3
Zapisz wzór funkcji
f
przesuniętej o wektor
~
u
.
y = x
2
~
u = [2, 3]
y =
1
x
~
u = [−3, −5]
y = sin x ~
u =
−
1
2
, 0
y = x
3
~
u = [−1, 4]
y = |x| ~
u = [0, −7]
y = 2
x
~
u = [0, 8]
Rozwiązanie
:
y = x
2
[
2
,
3
]
y = (x −
2
)
2
+
3
y = x
3
[
−1
,
4
]
y = (x − (
−1
))
3
+ 4 = (x + 1)
3
+ 4
y =
1
x
[
−3
,
−5
]
y =
1
x−(
−3
)
− 5 =
1
x+3
− 5
y = |x|
[
0
,
−7
]
y = |x|
−7
y = sin x
−
1
2
,
0
y = sin(x − (
−
1
2
)) = sin(x +
1
2
)
y = 2
x
[
0
,
8
]
y = 2
x
+
8
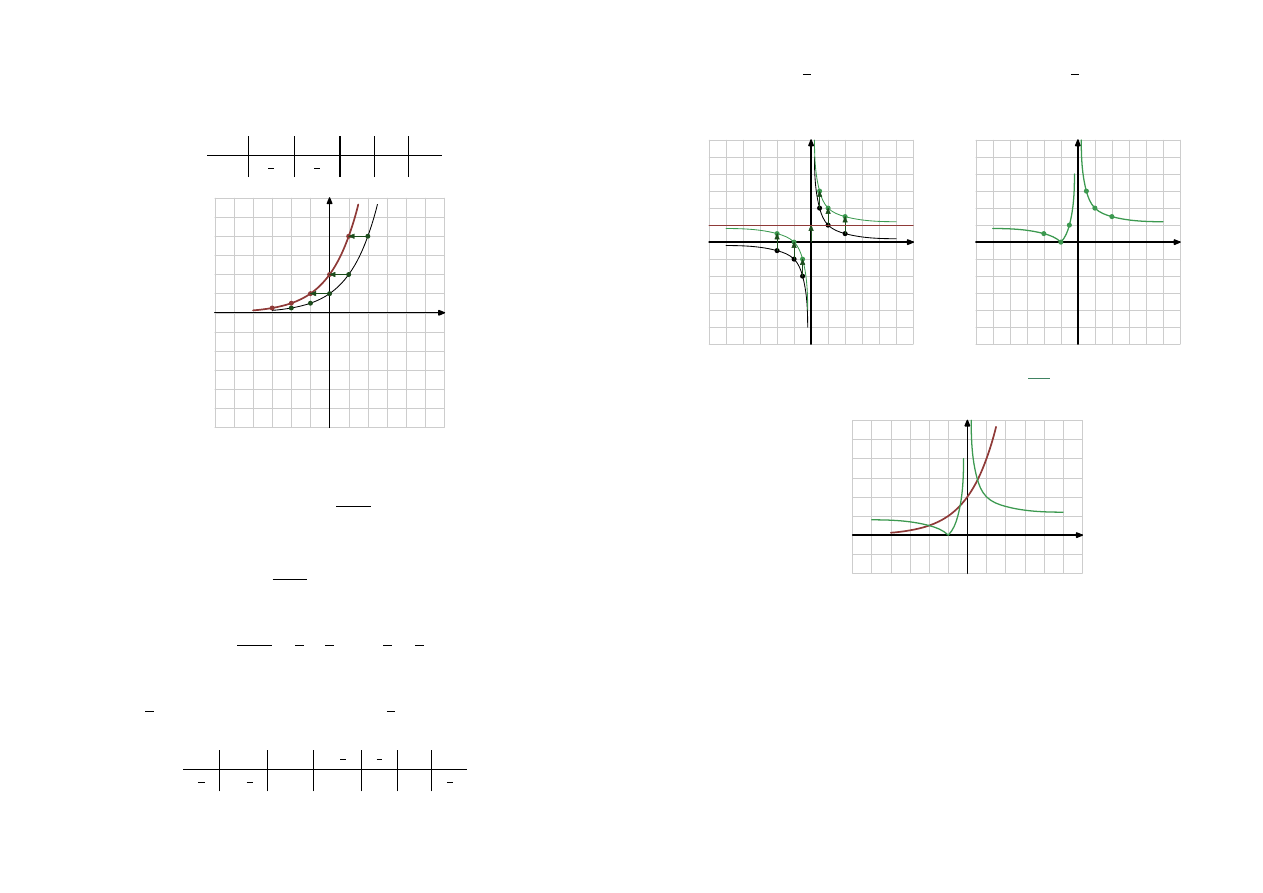
Naszkicuj w jednym układzie współrzędnych wykresy funkcji
f (x) = 2
x+1
oraz
g(x) =
x+1
x
.
Na podstawie wykonanego rysunku określ liczbę ujemnych rozwiązań równania
f (x) = g(x)
.
—
19
—
Rozwiązanie
:
Wykres
f (x) = 2
x+1
otrzymuję przez
f (x) = 2
x
o wektor
[−1, 0]
x
−2
−1
0
1
2
2
x
1
4
1
2
1
2
4
x
y
g(x) =
x + 1
x
Na początek narysuję wykres
y =
x + 1
x
y =
x + 1
x
=
x
x
+
1
x
= 1 +
1
x
=
1
x
+ 1
Wykres
y =
1
x
+ 1
otrzymuję przez
y =
1
x
o wektor
[0, 1]
x
−2
−1
−
1
2
1
2
1
2
1
x
−
1
2
−1
−2
2
1
1
2
y =
1
x
+ 1
y =
1
x
+ 1
x
y
x
y
Rysuję na jednym wykresie
f (x) = 2
x+1
i
g(x) =
x+1
x
i na podstawie rysunku okre-
ślam liczbę ujemnych rozwiązań równania
f (x) = g(x)
.
x
y
Wykresy przecinają się w trzech punktach, ale tylko dwa punkty przecięcia są dla
x < 0
.
Odp. Równanie
f (x) = g(x)
ma dwa ujemne rozwiązania.
Rysunek przedstawia fragment wykresu funkcji liniowej
f
. Wykres funkcji
g
jest obrazem wy-
kresu funkcji
f
otrzymanym za pomocą przesunięcia o wektor
~
u = [2, 1]
. Wyznacz miejsce
zerowe funkcji
g
.
—
20
—
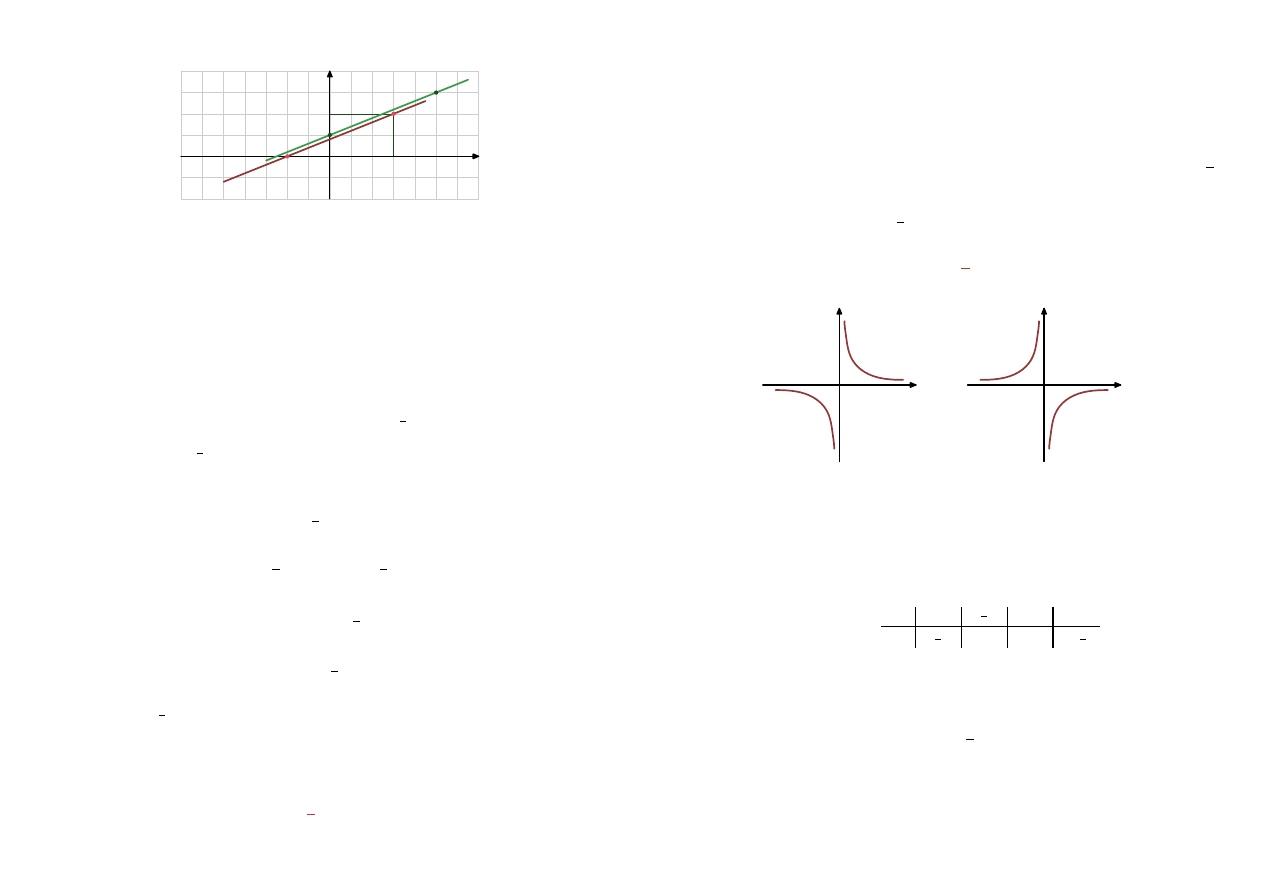
Rozwiązanie
:
x
y
f
g
1
2
3
4
5
6
−1
A
−3
−4
−5
−6
1
2
3
−1
B
A
0
B
0
Przesuwając
A
= (−2, 0)
o
~
u = [2, 1]
otrzymuję
A
0
= (
0
,
1
)
Przesuwając
B
= (3, 2)
o
~
u = [2, 1]
otrzymuję
B
0
= (
5
,
3
)
Równanie prostej przechodzącej przez punkty
A
0
= (
0
,
1
)
i
B
0
= (
5
,
3
)
(y −
1
) (
5
−
0
) − (
3
−
1
) (x −
0
) = 0
(y − 1)5 − 2x = 0
5y − 5 − 2x = 0
5y = 2x + 5
.
: 5
y =
2
5
x + 1
Wzór funkcji
g
:
y =
2
5
x + 1
Wyznaczam
0 =
2
5
x + 1
−
2
5
x = 1
.
:
−
2
5
x = −1 ·
5
2
x = −2
1
2
Odp.
x
0
= −2
1
2
Proporcjonalność odwrotna
Wielkości związane zależnością
y =
a
x
a 6= 0
nazywamy
odwrotnie proporcjonalnymi
.
R \ {0}
R \ {0}
Przykłady:
Czas przejazdu
t
z miasta do miasta jest odwrotnie proporcjonalny do prędkości
v
:
t =
s
v
Liczba litrów benzyny
n
jest odwrotnie proporcjonalna do ceny
c
, jeżeli tankujemy za każdym
razem za tą samą sumę
s
:
n =
s
c
Wykresem proporcjonalności odwrotnej
y =
a
x
jest
x
y
a > 0
x
y
a < 0
Czy wielkości
x
i
y
są odwrotnie proporcjonalne?
Rozwiązanie
:
x
−2
1
2
1
2
y
1
2
−2
−1
−
1
2
Przkształcam wzór proporcjanonalności odwrotnej
y =
a
x
· x
y · x = a
x · y =
a
—
21
—
Pary liczb są odwrotnie proporcjonalne, jeżeli ich iloczyn
a
jest taki sam.
−2 ·
1
2
= −1
1
2
· (−2) = −1
1 · (−1) = −1
2 · −
1
2
= −1
Odp. Wielkości
x
i
y
są odwrotnie proporcjonalne.
x
−5
−1
1
5
y
−2
−8
8
2
−5 · (−2) = 10
−1 · (−8) = 8
Dalej już nie trzeba sprawdzać, bo dla dwóch pierwszych par iloczyn jest różny.
Odp. Wielkości
x
i
y
nie są odwrotnie proporcjonalne.
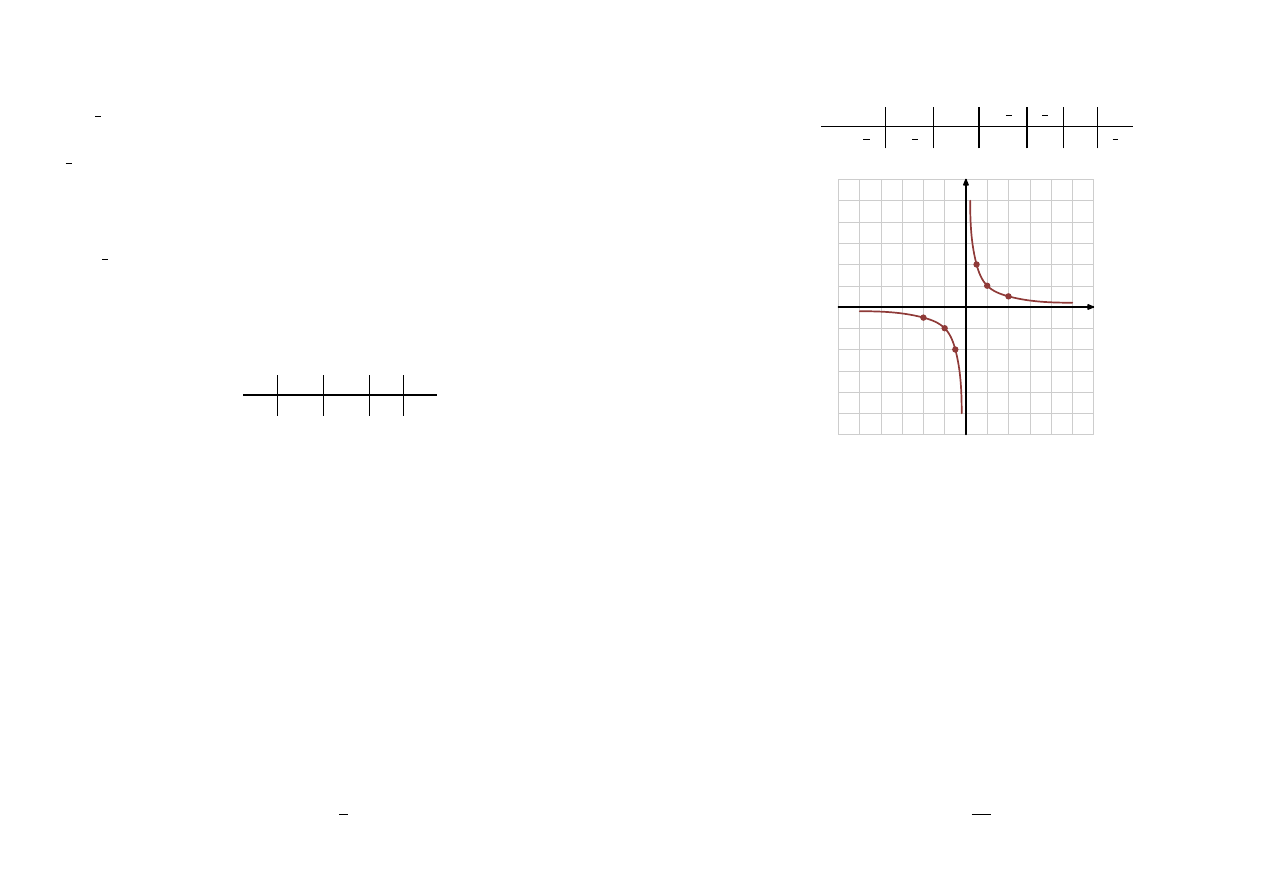
Narysuj wykres funkcji i wypisz jej własności:
y =
1
x
Rozwiązanie:
x
−2
−1
−
1
2
1
2
1
2
y =
1
x
−
1
2
−1
−2
2
1
1
2
x
y
D = R \ {0}
ZW = R \ {0}
nie ma
funkcja jest przedziałami monotoniczna
malejąca w przedziałach
(−∞, 0)
i
(0, ∞)
funkcja jest różnowartościowa
funkcja jest nieparzysta
funkcja nie jest okresowa
Narysuj wykres funkcji i wypisz jej własności:
y =
−2
x
—
22
—
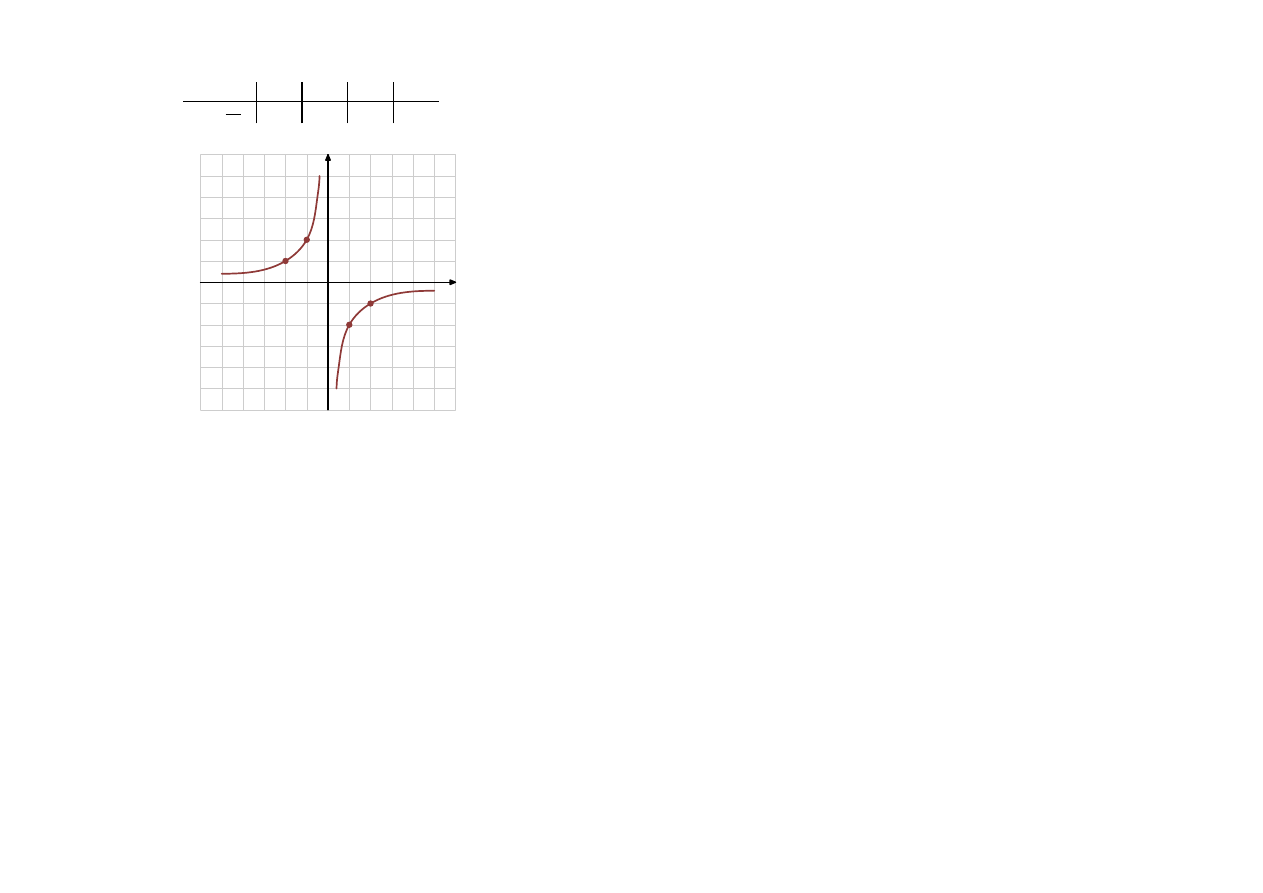
Rozwiązanie:
x
−2
−1
1
2
y =
−2
x
1
2
−2
−1
x
y
D = R \ {0}
ZW = R \ {0}
nie ma
funkcja jest przedziałami monotoniczna
rosnąca w przedziałach
(−∞, 0)
i
(0, ∞)
funkcja jest różnowartościowa
funkcja jest nieparzysta
funkcja nie jest okresowa
—
23
—
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron