WM

Z13/4. STATECZNOŚĆ PRĘTÓW ŚCISKANYCH OSIOWO – ZADANIE 4

1

Z13/4. STATECZNOŚĆ PRĘTÓW ŚCISKANYCH OSIOWO – ZADANIE 4

Z13/4.1. Zadanie 4

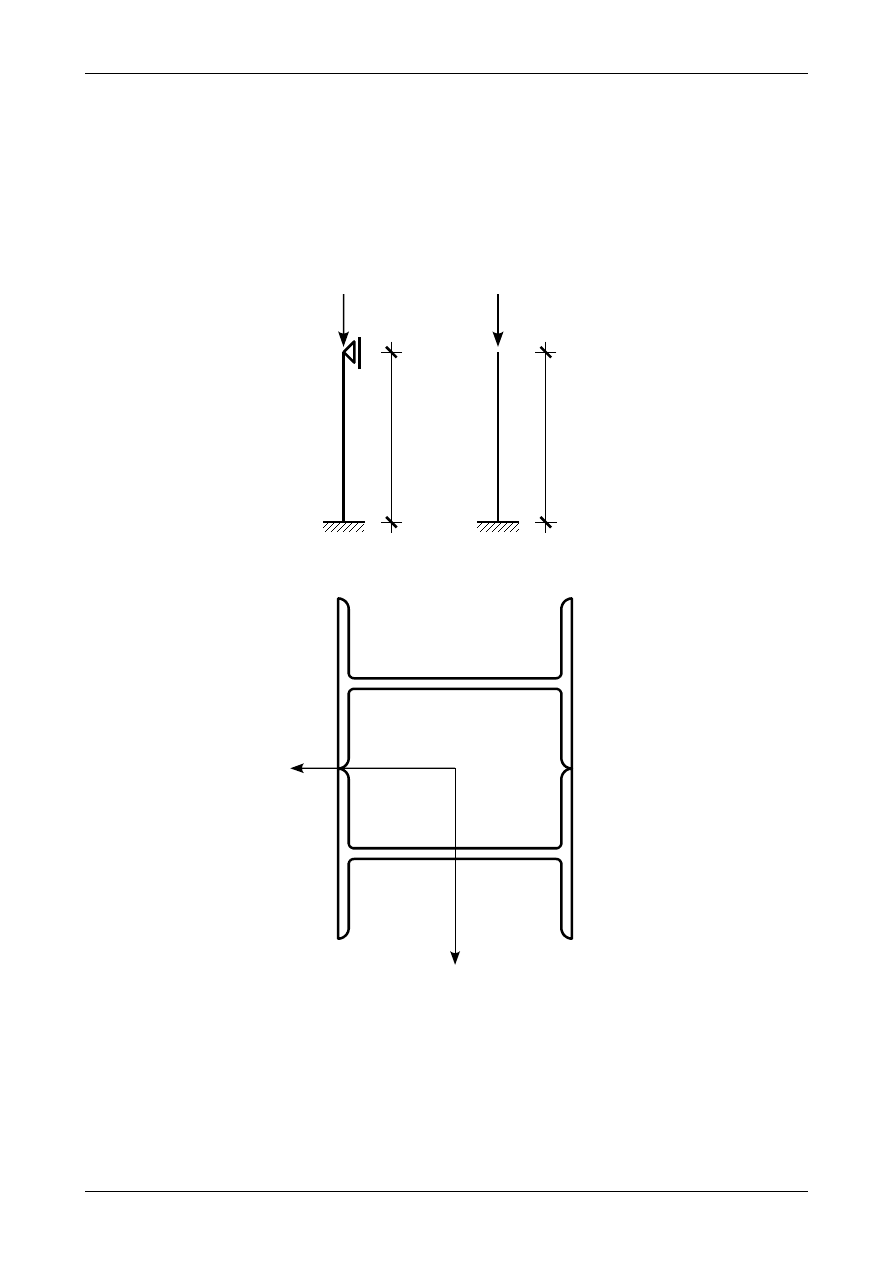
Wyznaczyć siłę krytyczną pręta ściskanego osiowo przedstawionego na rysunku Z13/4.1. Pręt ten jest

zamocowany w obu płaszczyznach pokrywających się z osiami głównymi bezwładności w różny sposób.
Długość pręta podana jest w metrach. Przekrój pręta stanowią dwa dwuteowniki szerokostopowe HEB300
przedstawione na rysunku Z13/4.2.

Płaszczyzna XY

Płaszczyzna XZ

P

KR

8,0

[m]

P

KR

8,

0

[m]

Rys. Z13/4.1. Pręt ściskany osiowo

Z=Z

0

=Z

gl

Y=Y

0

=Y

gl

HEB300

HEB300

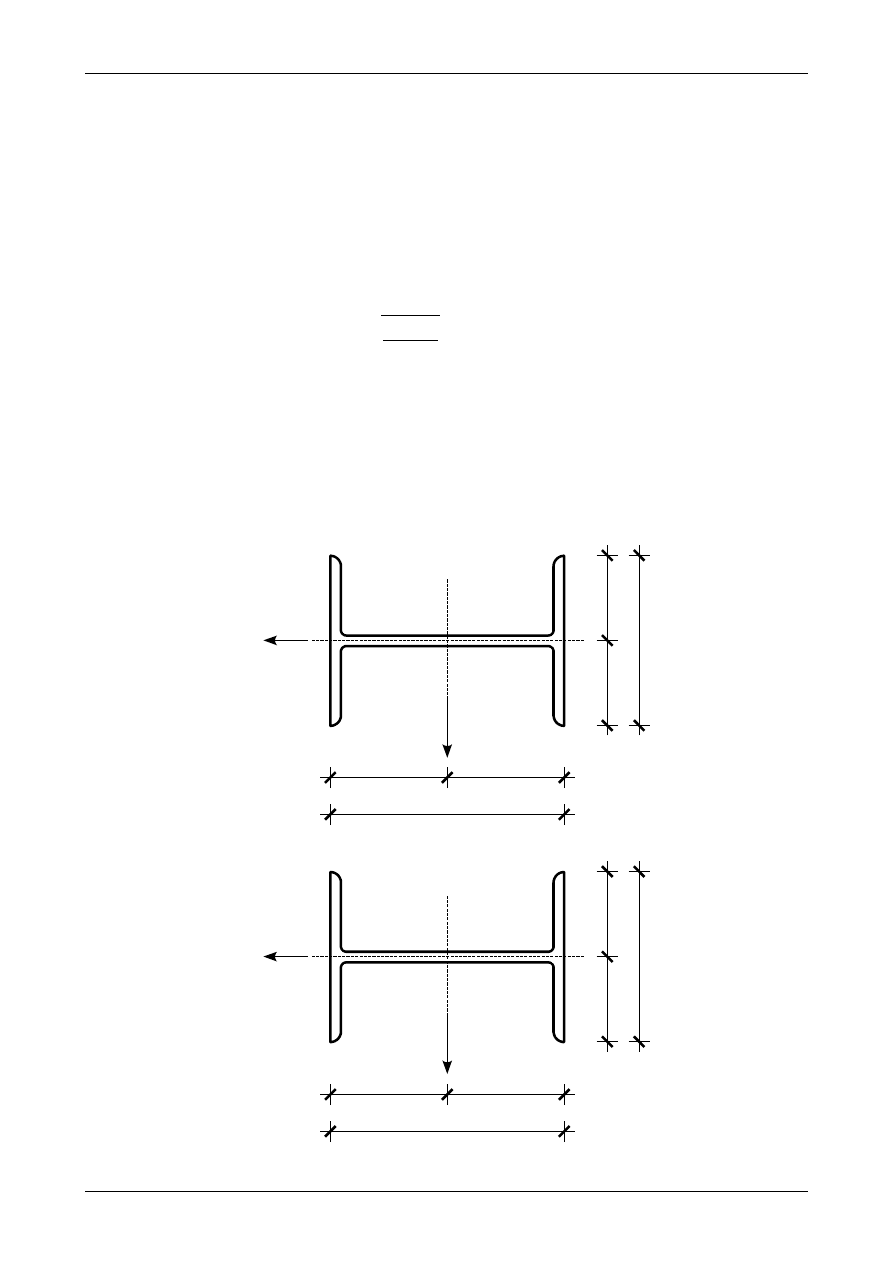
Rys. Z13/4.2. Przekrój pręta ściskanego osiowo

Pręt został wykonany ze stali o granicy proporcjonalności



H

=

205,0 MPa

(Z13/4.1)

oraz granicy plastyczności

Dr inż. Janusz Dębiński

WM

Z13/4. STATECZNOŚĆ PRĘTÓW ŚCISKANYCH OSIOWO – ZADANIE 4

2



P

=

235,0 MPa

.

(Z13/4.2)

Moduł Younga dla stali wynosi

E=205GPa=205000 MPa

.

(Z13/4.3)

Smukłość graniczna pręta wynosi



GR

=⋅



205000

205,0

=

99,35

.

(Z13/4.4)

Z13/4.2. Charakterystyki geometryczne przekroju pręta

Ponieważ osie Y i Z są osiami symetrii przekroju pręta więc środek ciężkości znajduje się w punkcie

ich przecięcia. Osie te będą także osiami głównymi przekroju, ponieważ jak wiadomo dewiacyjny moment
bezwładności w układzie współrzędnych, w którym przynajmniej jedna oś jest osią symetrii wynosi zero.
Moment ten równa się zero także w układzie osi głównych bezwładności.

Y

01

Z

01

30

,0

15

,0

15

,0

30,0

15,0

15,0

[cm]

X

X

Y

Y

Y

02

Z

02

30

,0

15

,0

15

,0

30,0

15,0

15,0

[cm]

X

X

Y

Y

Rys. Z/13/4.3. Dwuteowniki HEB300

Dr inż. Janusz Dębiński

WM

Z13/4. STATECZNOŚĆ PRĘTÓW ŚCISKANYCH OSIOWO – ZADANIE 4

3

Rysunek Z13/4.3 przedstawia pojedyncze dwuteowniki HEB z zaznaczonymi ich układami osi

środkowych oraz osi X i Y używanych w tablicach do projektowania konstrukcji metalowych. Jak widać na
rysunku Z13/4.3 momenty bezwładności pojedynczego dwuteownika w jego osiach środkowych będą
wynosiły

J

Y01

=

J

Y02

=

J

Y



T 

=

8560 cm

4

,

(Z13/4.5)

J

Z01

=

J

Z02

=

J

X



T 

=

25170 cm

4

.

(Z13/4.6)

Pole powierzchni pojedynczego dwuteownika wynosi

A

1

=

A

2

=

149 cm

2

.

(Z13/4.7)

Z=Z

0

=Z

gl

Y=Y

0

=Y

gl

Y

01

Z

01

Y

02

Z

02

30

,0

30

,0

15

,0

15

,0

15

,0

15

,0

30,0

15,0

15,0

[cm]

sc

1

sc

2

sc

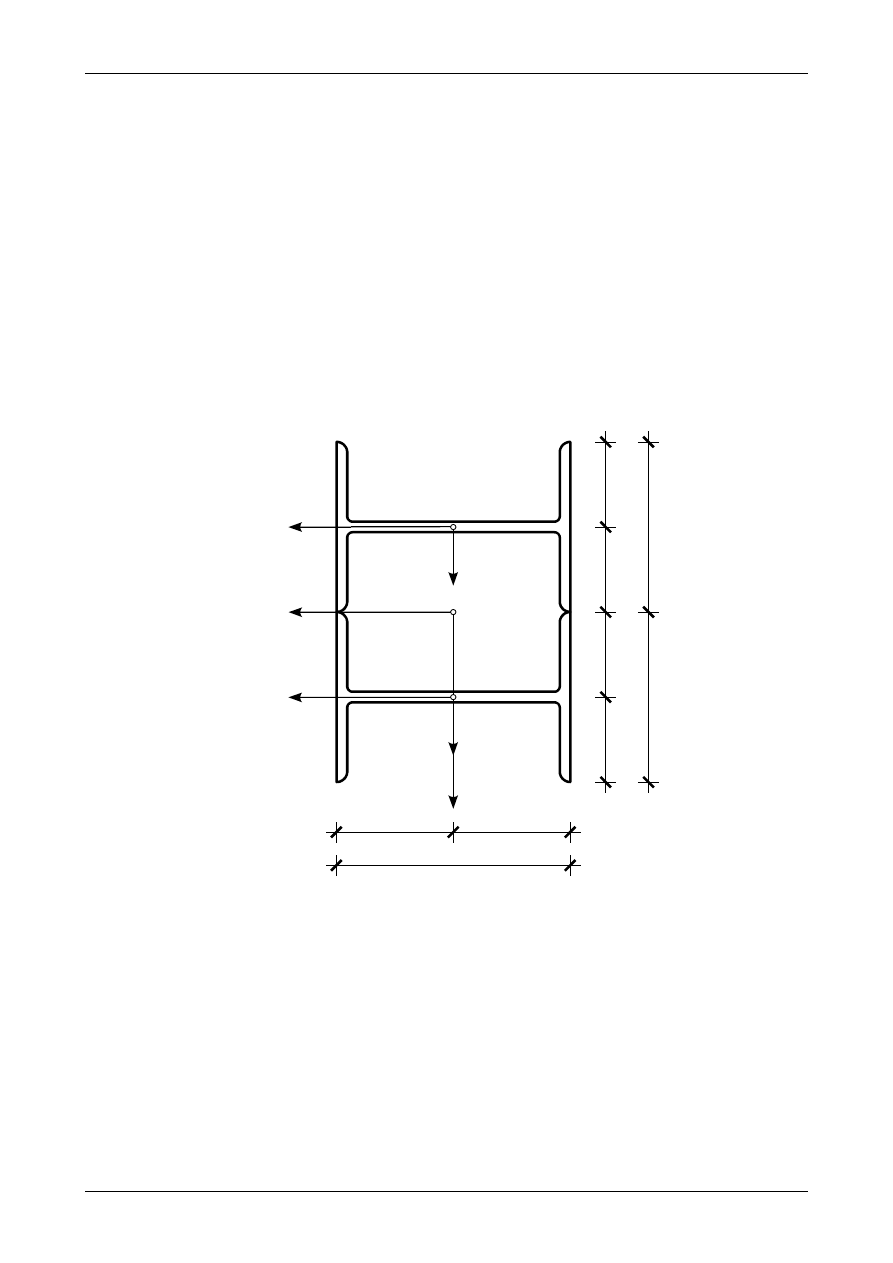
Rys. Z13/4.4. Przekrój pręta ściskanego osiowo

Rysunek Z13/4.4 przedstawia przekrój pręta z zaznaczonymi środkami ciężkości poszczególnych

dwuteowników.Współrzędne środków ciężkości dwuteowników w układzie osi głównych wynoszą

y

01

=

0,0 cm

z

01

=−

15,0 cm

,

(Z13/4.8)

y

02

=

0,0 cm

z

02

=

15,0 cm

.

(Z13/4.9)

Dr inż. Janusz Dębiński

WM

Z13/4. STATECZNOŚĆ PRĘTÓW ŚCISKANYCH OSIOWO – ZADANIE 4

4

Moment bezwładności względem osi Y=Y

gl

wynosi

J

Y

=

J

Ygl

=

8560



−

15,0



2

⋅

149,08560



15,0



2

⋅

149,0=84170 cm

4

.

(Z13/4.10)

Moment bezwładności względem osi Z=Z

gl

wynosi

J

Z

=

J

Zgl

=

25170



0,0



2

⋅

149,025170



0,0



2

⋅

149,0=50340 cm

4

.

(Z13/4.11)

Pole powierzchni całego przekroju wynosi

A=149,0149,0=298,0 cm

2

.

(Z13/4.12)

Z13/4.3. Siła krytyczna

Płaszczyzna XY jest prostopadła do głównej osi bezwładności Z=Z

gl

. Wszystkie wielkości będą więc

miały indeks Z. Promień bezwładności w płaszczyźnie XY zgodnie z (13.21) wynosi

i

Z

=



50340

298,0

=

13,0 cm

.

(Z13/4.13)

Długość wyboczeniowa w płaszczyźnie XY wynosi

L

W



Z 

=

0,7⋅8,0=5,6 m=560,0 cm

.

(Z13/4.14)

Smukłość pręta w płaszczyźnie XY zgodnie z (13.22) wynosi



Z

=

560,0

13,0

=

43,08

.

(Z13/4.15)

Płaszczyzna XZ jest prostopadła do głównej osi bezwładności Y=Y

gl

. Wszystkie wielkości będą więc

miały indeks Y. Promień bezwładności w płaszczyźnie XZ zgodnie z (13.23) wynosi

i

Y

=



84170

298,0

=

16,81 cm

.

(Z13/4.16)

Długość wyboczeniowa w płaszczyźnie XZ wynosi

L

W



Y 

=

2,0⋅8,0=16,0 m=1600 cm

.

(Z13/4.17)

Smukłość pręta zgodnie z (13.24) w płaszczyźnie XZ wynosi

Dr inż. Janusz Dębiński

WM

Z13/4. STATECZNOŚĆ PRĘTÓW ŚCISKANYCH OSIOWO – ZADANIE 4

5

50

100

150

200

250

300

0

0

50

100

150

200

250

A

λ

σ

KR

[MPa]

σ

H

=205 MPa

λ

G

R

=

99

,35

λ

=

95

,1

8

σ

KR

=206,3 MPa

σ

P

=235 MPa

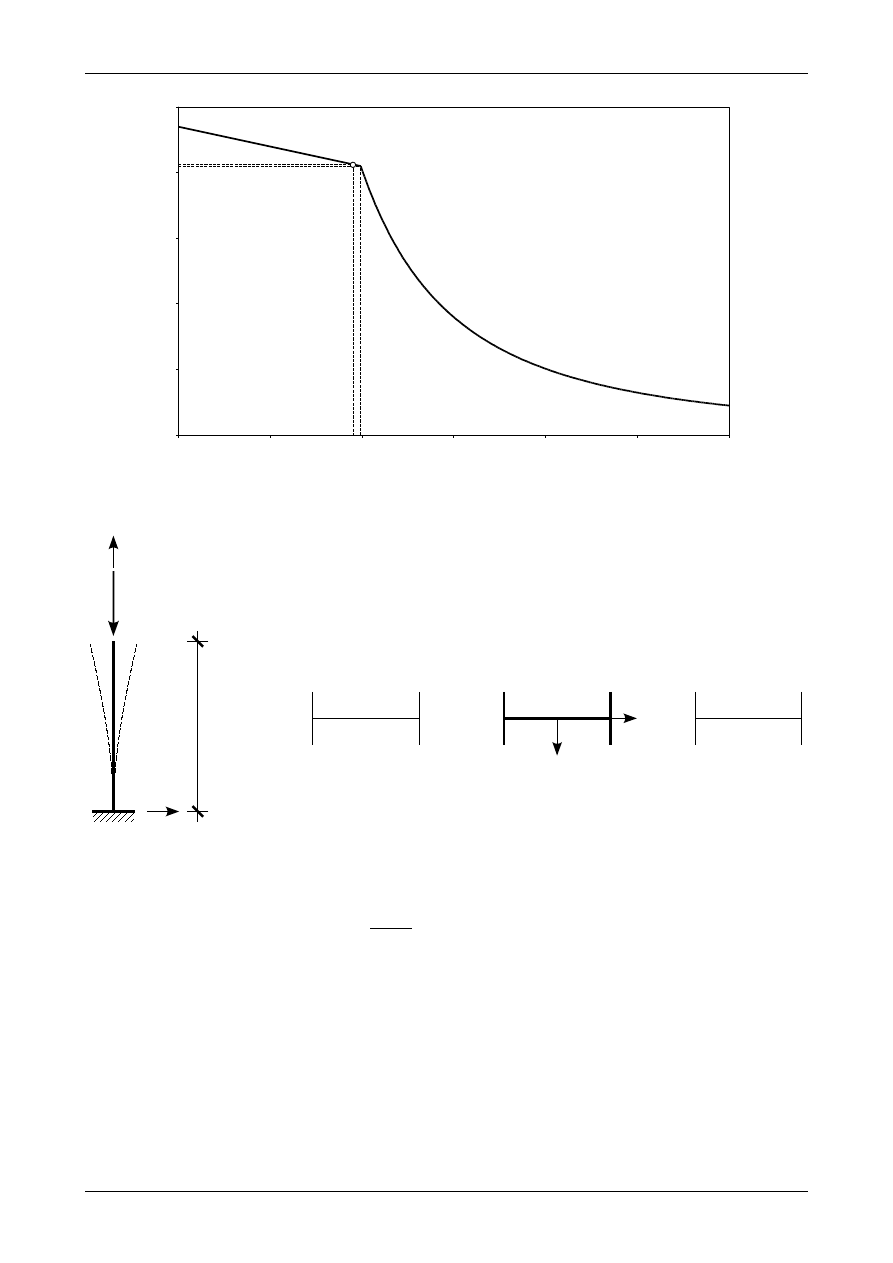
Rys. Z13/4.5. Położenie punktu krytycznego w płaszczyźnie wyboczenia XZ

8,0

P

KR

X

Z

[m]

Z=Z

gl

Y=Y

gl

Rys. Z13/4.6. Postać wyboczeniowa pręta w płaszczyźnie wyboczenia XZ



Y

=

1600

16,81

=

95,18

.

(Z13/4.18)

Maksymalna smukłość pręta, zgodnie z (13.25), wynosi

=

Y

=

95,18

.

(Z13/4.19)

Wyboczenie nastąpi więc w płaszczyźnie XZ. Największa smukłość jest mniejsza niż smukłość graniczna
więc pręt pracuje w zakresie sprężysto-plastycznym. Normalne naprężenie krytyczne zgodnie ze wzorem
(13.11) wynosi

Dr inż. Janusz Dębiński

WM

Z13/4. STATECZNOŚĆ PRĘTÓW ŚCISKANYCH OSIOWO – ZADANIE 4

6



KR

=

235,0 −

235,0−205,0

99,35

⋅

95,18=206,3 MPa=20,63

kN

cm

2

.

(Z13/4.20)

Siła krytyczna zgodnie ze wzorem (13.20) będzie więc wynosić

P

KR

=

20,63⋅298,0=6148 kN

.

(Z13/4.21)

Rysunek Z13/4.5 przedstawia położenie punktu krytycznego w płaszczyźnie wyboczenia XZ. Rysunek

Z13/4.6 przedstawia postać wyboczeniową pręta w płaszczyźnie wyboczenia XZ.

Dr inż. Janusz Dębiński