www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
L
UBELSKA PRÓBA PRZED MATUR ˛
A
DLA KLAS TRZECICH
POZIOM PODSTAWOWY
GRUPA
I
25
LUTEGO
2014
C
ZAS PRACY
: 170
MINUT
Zadania zamkni˛ete
Z
ADANIE
1
(1
PKT
)
Liczba
1
3
·
3
−2
·
3
3
3
−3
·
√
81
·
3
2
:27
0
−
1
jest równa
A) 3
−
1
B) 3
−
2
C) 3
1
D) 3
2
R
OZWI ˛
AZANIE
Liczymy
3
−
1
·
3
−
2
·
3
3
3
−
3
·
3
2
·
3
2
: 1
−
1
= =
3
−
1
−
2
+
3
3
−
3
+
2
+
2
−
1
=
1
3
−
1
=
3.
Odpowied´z: C
Z
ADANIE
2
(1
PKT
)
Liczba
(
2
−
√
3
)
2
−
2
(
2
−
2
√
3
)
jest równa
A)
−
√
3
B) 3
C) 4
−
√
3
D) 4
+
√
3
R
OZWI ˛
AZANIE
Liczymy korzystaj ˛
ac ze wzoru skróconego mno ˙zenia
(
a
−
b
)
2
=
a
2
−
2ab
+
b
2
.
Mamy wi˛ec
(
2
−
√
3
)
2
−
2
(
2
−
2
√
3
) =
4
−
4
√
3
+
3
−
4
+
4
√
3
=
3.
Odpowied´z: B
Z
ADANIE
3
(1
PKT
)
Liczb ˛
a odwrotn ˛
a do liczby
1
2
−
√
2
+
1
2
+
√
2
jest liczba
A)
−
2
B) 2
C)
1
2
D) 2
√
2
Materiał pobrany z serwisu
1

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Zauwa ˙zmy, ˙ze (sprowadzamy ułamki do wspólnego mianownika)
a
=
1
2
−
√
2
+
1
2
+
√
2
=
(
2
+
√
2
) + (
2
−
√
2
)
(
2
−
√
2
)(
2
+
√
2
)
=
4
4
−
2
=
2.
Zatem
1
a
=
1
2
.
Odpowied´z: C
Zadania
.info
Podobają Ci się nasze rozwiązania?
Pokaż je koleżankom i kolegom ze szkoły!
Z
ADANIE
4
(1
PKT
)
Cen˛e ksi ˛
a ˙zki obni ˙zono o 20%, a po miesi ˛
acu now ˛
a cen˛e obni ˙zono o dalsze 10%. W wyniku
obu obni ˙zek cena ksi ˛
a ˙zki zmniejszyła si˛e o
A) 25%
B) 28%
C) 29%
D) 30%
R
OZWI ˛
AZANIE
Oznaczmy przez x wyj´sciow ˛
a cen˛e nart. Zatem po pierwszej obni ˙zce cena wynosiła
0, 8x.
Po kolejnej obni ˙zce cena wynosiła
0, 9
·
0, 8x
=
0, 72x.
Zatem cena została ł ˛
acznie obni ˙zona o 28%.
Odpowied´z: B
Z
ADANIE
5
(1
PKT
)
Warto´s´c liczbowa wyra ˙zenia 5 log
2
2
−
log
2
2 jest równa
A) 2
−
1
B) 2
0
C) 2
1
D) 2
2
R
OZWI ˛
AZANIE
Poniewa ˙z log
2
2
=
1, wi˛ec
5 log
2
2
−
log
2
2
=
5
−
1
=
4
=
2
2
.
Odpowied´z: D
Materiał pobrany z serwisu
2
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
6
(1
PKT
)
Liczba 5 jest pierwiastkiem wielomianu W
(
x
) =
x
3
−
5x
2
+
ax
+
10. Współczynnik a jest
równy
A)
−
2
B)
−
5
C) 2
D) 5
R
OZWI ˛
AZANIE
Liczymy
0
=
W
(
5
) =
125
−
125
+
5a
+
10
=
10
+
5a
−
10
=
5a
/ : 5
−
2
=
a.
Odpowied´z: A
Z
ADANIE
7
(1
PKT
)
Rozwi ˛
azaniem nierówno´sci
|
x
+
8
|
6 3 jest zbiór
A)
h−
11,
−
5
i
B)
h−
11, 5
i
C)
h
5, 11
i
D)
h−
5, 11
i
R
OZWI ˛
AZANIE
Sposób I
Liczymy
|
x
+
8
|
6 3
−
3 6 x
+
8 6 3 /
−
8
−
11 6 x 6
−
5.
Zatem x
∈ h−
11,
−
5
i
.
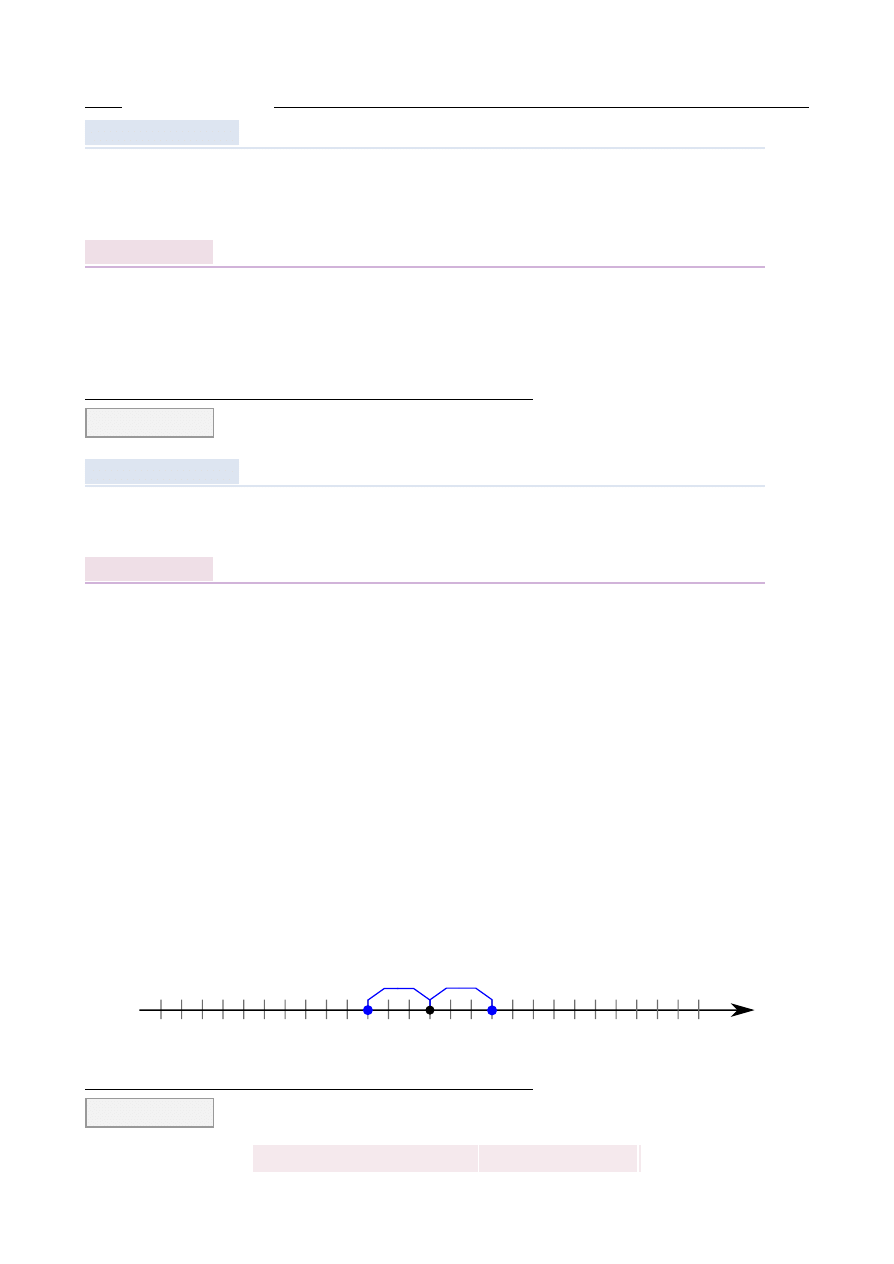
Sposób II
Dan ˛
a nierówno´s´c mo ˙zemy zapisa´c w postaci:
|
x
− (−
8
)|
6 3.
Zatem szukamy tych liczb, które na osi liczbowej s ˛
a oddalone od
−
8 o nie wi˛ecej ni ˙z 3.
Wykonujemy rysunek
-10 -9
-6
-8 -7
-5 -4 -3
3
3
0
-2 -1
-11
-12
Teraz ju ˙z łatwo odczyta´c, ˙ze zbiorem rozwi ˛
aza ´n jest
h−
11,
−
5
i
.
Odpowied´z: A
Materiał pobrany z serwisu
3
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
8
(1
PKT
)
Długo´s´c odcinka AB o ko ´ncach w punktach A
= (−
1,
−
2
)
i B
= (−
4,
−
3
)
jest równa
A)
√
7
B)
√
10
C)
√
11
D)
√
13
R
OZWI ˛
AZANIE
Liczymy
AB
=
q
(−
4
− (−
1
))
2
+ (−
3
− (−
2
))
2
=
√
9
+
1
=
√
10.
Odpowied´z: B
Z
ADANIE
9
(1
PKT
)
W trójk ˛
acie równoramiennym rami˛e ma długo´s´c 5, a k ˛
at ostry przy podstawie jest równy α.
Wysoko´s´c poprowadzona na podstaw˛e trójk ˛
ata wynosi
A) 5 cos α
B) 5 tg α
C) 5 sin α
D) 5 ctg α
R
OZWI ˛
AZANIE
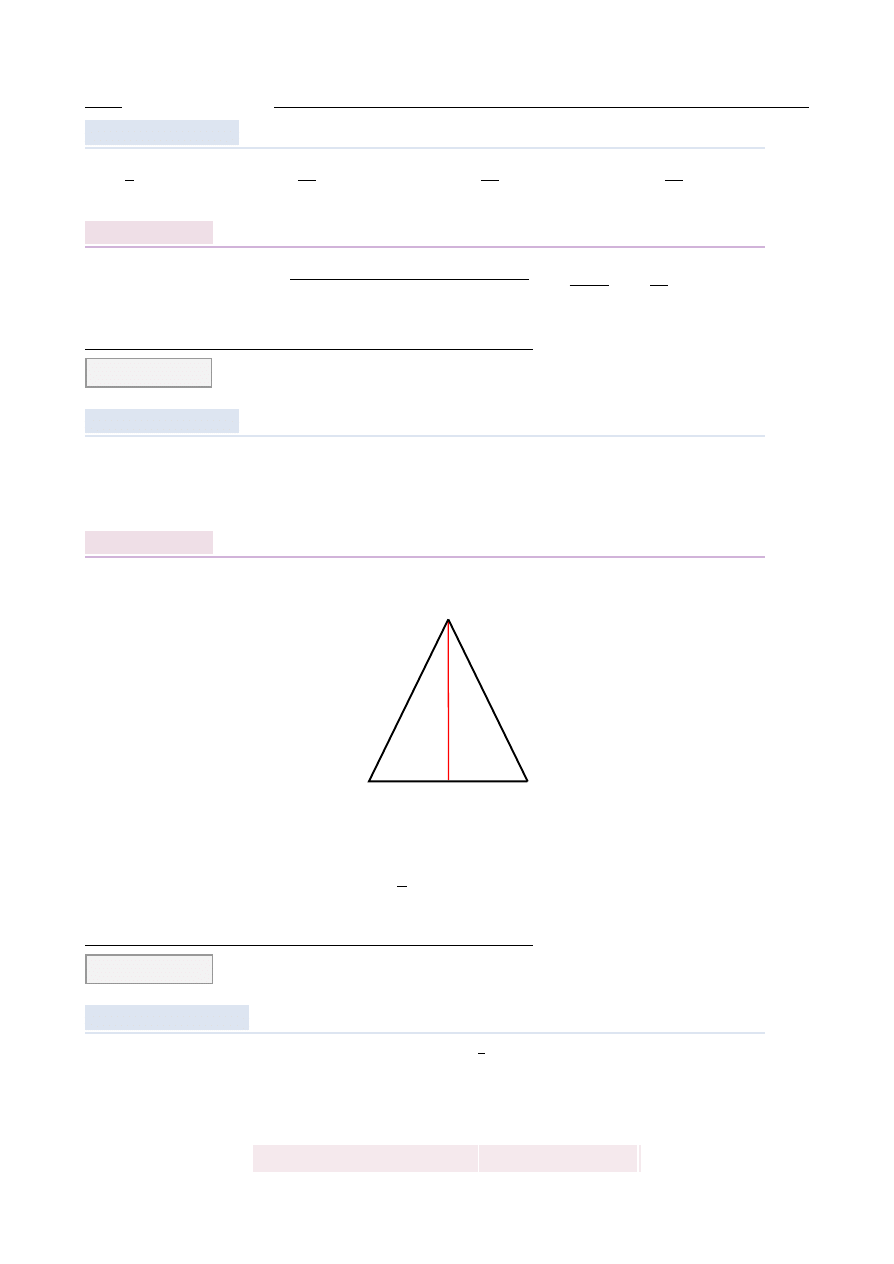
Zaczynamy od szkicowego rysunku.
A
B
C
D
5
5
α
h
W trójk ˛
acie prostok ˛
atnym ADC mamy
sin α
=
h
5
⇒
h
=
5 sin α.
Odpowied´z: C
Z
ADANIE
10
(1
PKT
)
Prosta prostopadła do prostej o równaniu y
=
1
2
x
−
2 i przechodz ˛
aca przez punkt A
=
(−
1, 3
)
ma równanie
A) y
= −
2x
−
2
B) y
=
2x
−
1
C) y
=
2x
+
2
D) y
= −
2x
+
1
Materiał pobrany z serwisu
4
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Proste y
=
ax
+
b oraz y
=
cx
+
d s ˛
a prostopadłe je ˙zeli ac
= −
1. Zatem szukana prosta musi
mie´c współczynnik kierunkowy (liczb˛e przy x) równy
−
2. W takim razie musi to by´c prosta
y
= −
2x
−
2 lub y
= −
2x
+
1. Sprawdzamy teraz, w przypadku której z tych prostych
otrzymamy y
=
3 po podstawieniu x
= −
1. Gdy to zrobimy, oka ˙ze si˛e, ˙ze szukan ˛
a prost ˛
a
jest y
= −
2x
+
1.
Odpowied´z: D
Z
ADANIE
11
(1
PKT
)
Rozwi ˛
azaniem równania
x
+
1
x
−
3
=
2
7
jest liczba
A) 2
3
5
B)
−
2
3
5
C) 2
3
7
D)
−
2
3
7
R
OZWI ˛
AZANIE
Liczymy
x
+
1
x
−
3
=
2
7
/
·
7
(
x
−
3
)
7x
+
7
=
2x
−
6
5x
= −
13
⇒
x
= −
13
5
= −
2
3
5
.
Odpowied´z: B
Z
ADANIE
12
(1
PKT
)
Zbiorem rozwi ˛
aza ´n nierówno´sci
−(
x
+
3
)(
x
−
5
)
> 0 jest
A)
h−
5,
−
3
i
B)
h
3, 5
i
C)
h−
3, 5
i
D)
h−
5, 3
i
R
OZWI ˛
AZANIE
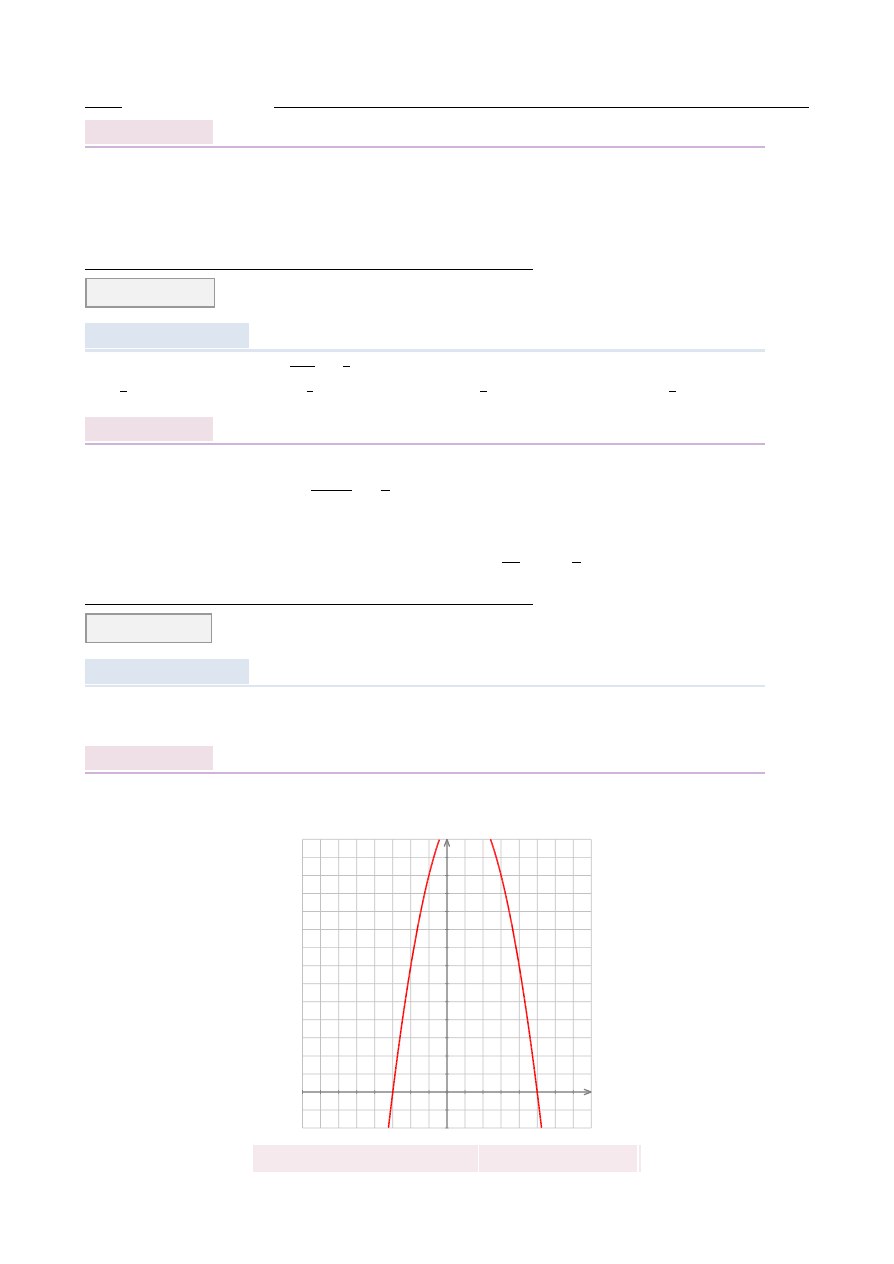
Wykresem funkcji kwadratowej z lewej strony nierówno´sci jest parabola o ramionach skie-
rowanych w dół i miejscach zerowych
−
3 i 5 (dla takich warto´sci x zeruj ˛
a si˛e nawiasy).
-5
-1
+5
x
-1
+1
+5
+10
y
Materiał pobrany z serwisu
5

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Zatem rozwi ˛
azaniem nierówno´sci jest zbiór
h−
3, 5
i
.
Odpowied´z: C
Z
ADANIE
13
(1
PKT
)
Najwi˛eksz ˛
a liczb ˛
a całkowit ˛
a nale ˙z ˛
ac ˛
a do zbioru rozwi ˛
aza ´n nierówno´sci x
+
1
3
6
x
2
jest
A)
−
2
B)
−
1
C) 1
D) 2
R
OZWI ˛
AZANIE
Przekształ´cmy dan ˛
a nierówno´s´c.
x
+
1
3
6
x
2
/
·
6
6x
+
2 6 3x
3x 6
−
2
/ : 3
x 6
−
2
3
.
Najwi˛eksza liczba całkowita spełniaj ˛
aca t˛e nierówno´s´c to
−
1.
Odpowied´z: B
Z
ADANIE
14
(1
PKT
)
Funkcja liniowa f
(
x
) = (
k
2
−
1
)
x
−
5 jest malej ˛
aca dla
A) k
∈ h−
1, 1
i
B) k
∈
R
\ {−
1, 1
}
C) k
∈
R
\ h−
1, 1
i
D) k
∈ (−
1, 1
)
R
OZWI ˛
AZANIE
Funkcja liniowa jest malej ˛
aca je ˙zeli współczynnik kierunkowy jest liczb ˛
a ujemn ˛
a. Rozwi ˛
a-
zujemy nierówno´s´c
k
2
−
1
<
0
(
k
−
1
)(
k
+
1
) <
0
k
∈ (−
1, 1
)
.
Odpowied´z: D
Z
ADANIE
15
(1
PKT
)
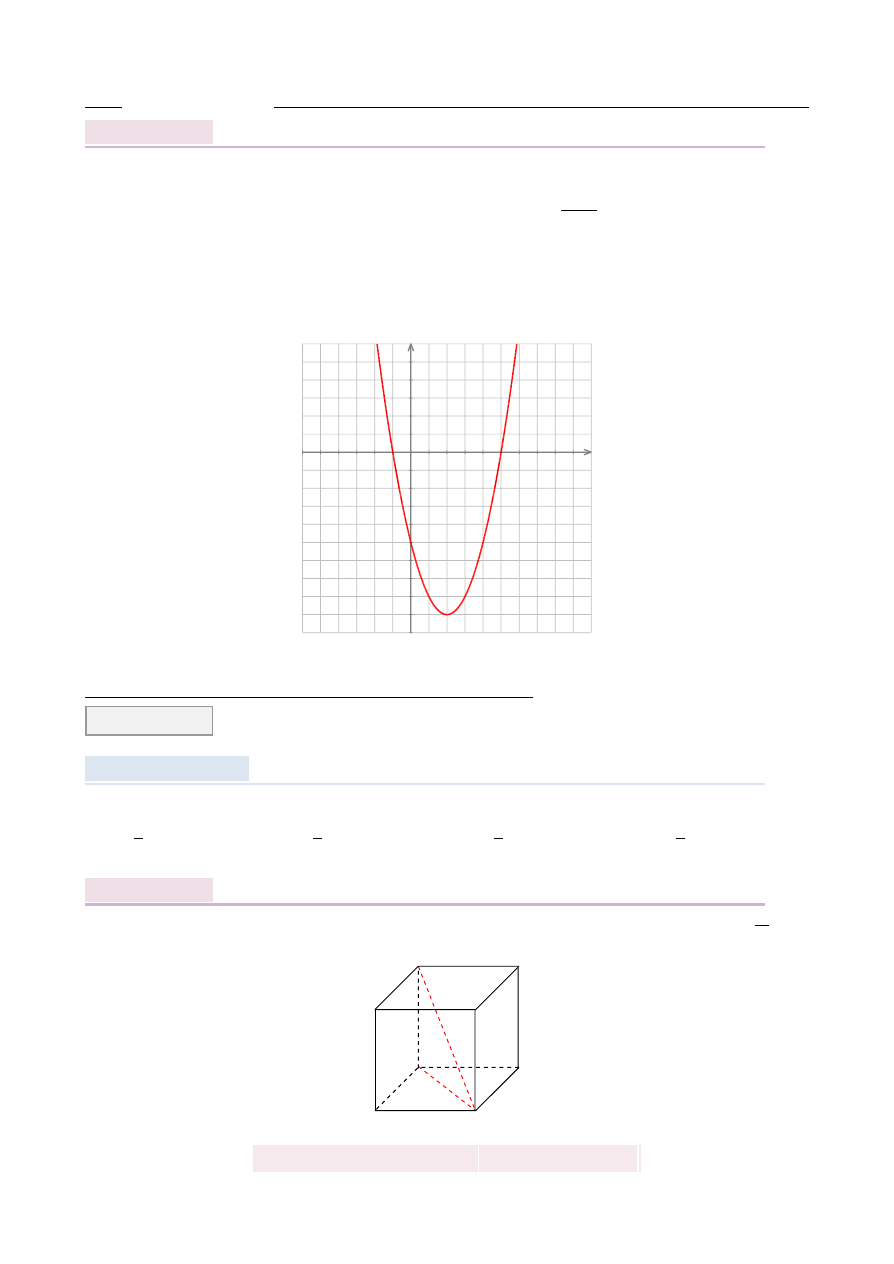
Najmniejsza warto´s´c funkcji f
(
x
) = (
x
+
1
)(
x
−
5
)
wynosi
A)
−
5
B) 5
C)
−
9
D)
−
1
Materiał pobrany z serwisu
6
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Wykresem podanej funkcji jest parabola o ramionach skierowanych w gór˛e i miejscach ze-
rowych
−
1 i 5. Wierzchołek tej paraboli znajduje si˛e dokładnie w ´srodku mi˛edzy pierwiast-
kami, czyli pierwsza współrz˛edna wierzchołka jest równa
−
1
+
5
2
=
2. Druga współrz˛edna
wierzchołka jest równa
f
(
2
) = (
2
+
1
)(
2
−
5
) =
3
· (−
3
) = −
9.
Jest to oczywi´scie najmniejsza warto´s´c funkcji.
-5
-1
+2
+5
x
-10
-5
-1
+1
y
Odpowied´z: C
Z
ADANIE
16
(1
PKT
)
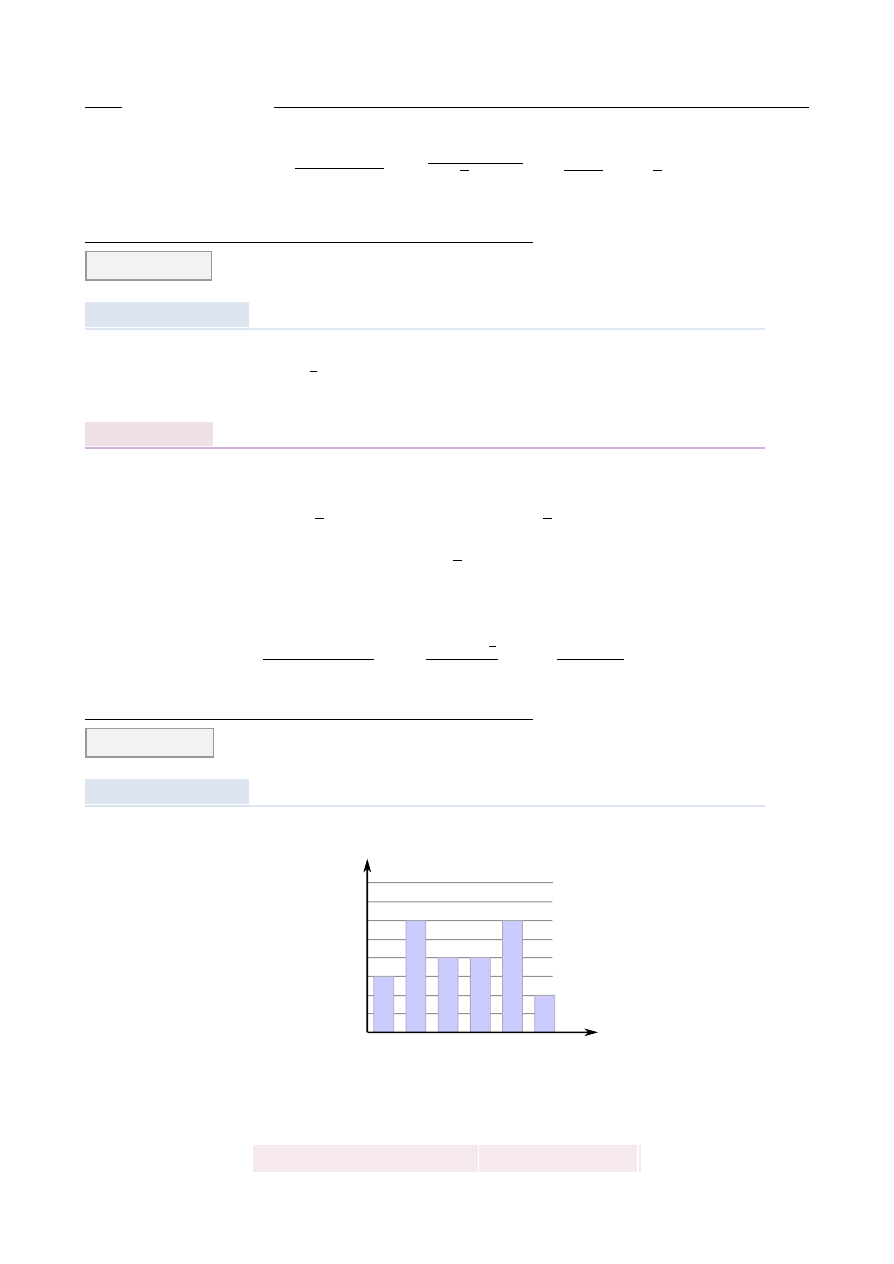
Suma długo´sci kraw˛edzi sze´scianu jest równa 60 cm. Długo´s´c przek ˛
atnej tego sze´scianu
wynosi
A) 5
√
2 cm
B) 5
√
3 cm
C) 3
√
5 cm
D) 2
√
5 cm
R
OZWI ˛
AZANIE
Sze´scian ma 12 kraw˛edzi, wi˛ec mamy do czynienia z sze´scianem o kraw˛edzi długo´sci
60
12
=
5.
d
A
B
C
5
5
5
Materiał pobrany z serwisu
7
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Je ˙zeli dorysujemy przek ˛
atn ˛
a kwadratu w podstawie to powinno by´c jasne, ˙ze
BC
=
p
AB
2
+
AC
2
=
q
(
5
√
2
)
2
+
5
2
=
√
3
·
25
=
5
√
3.
Odpowied´z: B
Z
ADANIE
17
(1
PKT
)
Suma dwudziestu pocz ˛
atkowych wyrazów niesko ´nczonego ci ˛
agu arytmetycznego
(
a
n
)
, w
którym a
1
=
0, 5 oraz a
3
=
3
1
2
jest równa
A) 295
B) 298
C) 305
D) 308
R
OZWI ˛
AZANIE
Obliczmy najpierw ró ˙znic˛e ci ˛
agu
3
1
2
=
a
3
=
a
2
+
r
=
a
1
+
2r
=
1
2
+
2r
2r
=
3
⇒
r
=
3
2
.
Suma pierwszych 20 wyrazów ci ˛
agu jest wi˛ec równa
S
20
=
2a
1
+ (
n
−
1
)
r
2
·
n
=
1
+
19
·
3
2
2
·
20
=
20
+
570
2
=
295.
Odpowied´z: A
Z
ADANIE
18
(1
PKT
)
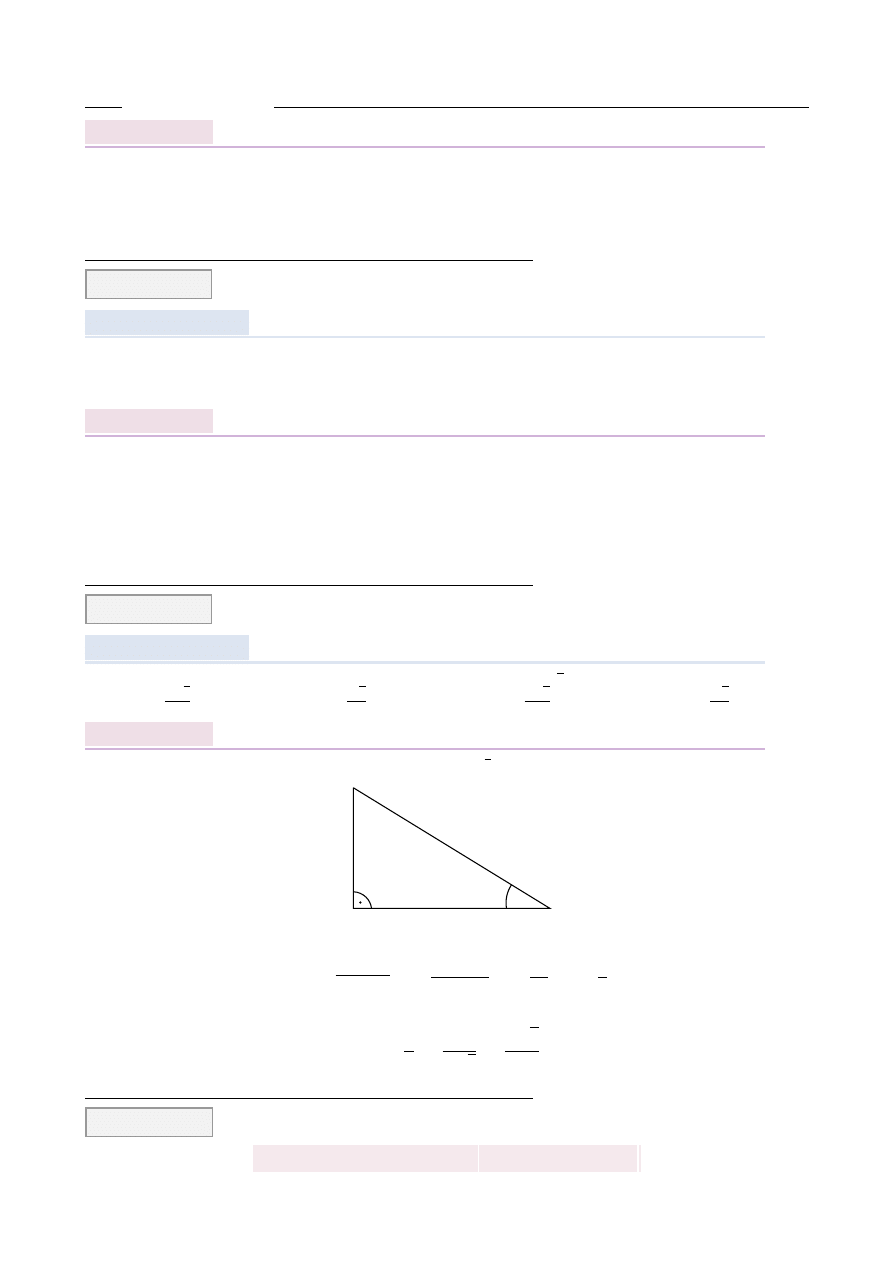
Na diagramie podano wzrost uczniów klasy I w pewnym liceum.
liczba osób
wzrost
0
1
2
3
4
5
6
7
8
158 160 164 166 168 170
Mediana wszystkich wyników jest równa
A) 163
B) 164
C) 165
D) 166
Materiał pobrany z serwisu
8
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
W sumie na diagramie przedstawiono informacje o wzro´scie
3
+
6
+
4
+
4
+
6
+
2
=
25
osób. Mediana jest wi˛ec równa wzrostowi 13-tej osoby, je ˙zeli uporz ˛
adkujemy te osoby we-
dług wzrostu. Poniewa ˙z 3
+
6
+
4
=
13, wi˛ec trzynasta osoba ma 164 cm wzrostu.
Odpowied´z: B
Z
ADANIE
19
(1
PKT
)
Liczby
−
8; x
−
2;
−
2 (w podanej kolejno´sci) s ˛
a pierwszym, drugim i trzecim wyrazem ci ˛
agu
geometrycznego. Wówczas liczba x mo ˙ze by´c równa
A) 4
B) 6
C) 7
D) 8
R
OZWI ˛
AZANIE
Je ˙zeli trzy liczby a, b, c s ˛
a kolejnymi wyrazami ci ˛
agu geometrycznego to b
2
=
ac. Daje to
nam równanie
(
x
−
2
)
2
= (−
8
) · (−
2
) =
16
x
−
2
= ±
4
x
= −
2
∨
x
=
6
Wida´c wi˛ec, ˙ze x mo ˙ze by´c równe 6.
Odpowied´z: B
Z
ADANIE
20
(1
PKT
)
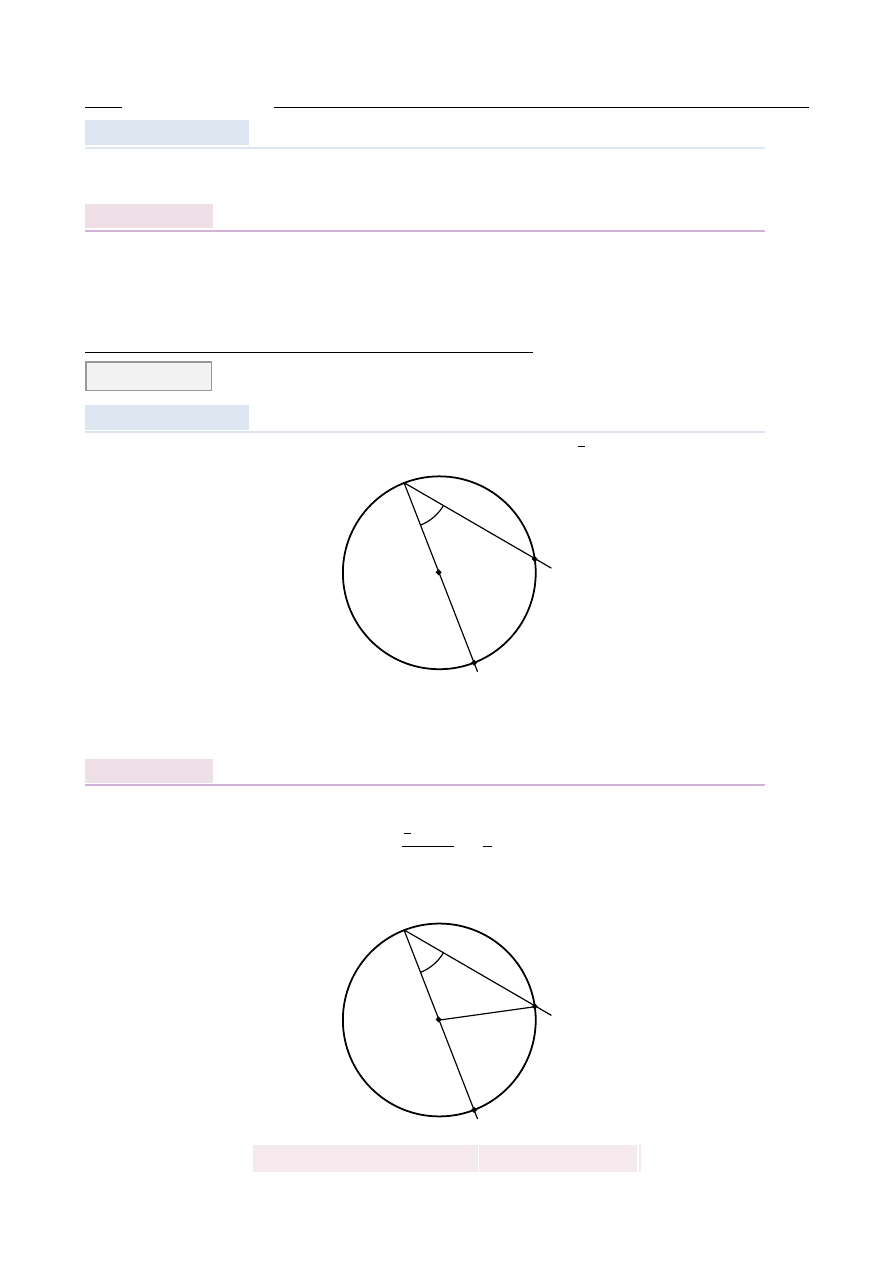
K ˛
at α jest k ˛
atem ostrym w trójk ˛
acie prostok ˛
atnym i sin α
=
5
7
. Wówczas
A) tg α
=
5
√
6
4
B) tg α
=
√
6
12
C) tg α
=
5
√
6
12
D) tg α
=
√
6
4
R
OZWI ˛
AZANIE
Szkicujemy trójk ˛
at prostok ˛
atny, w którym sin α
=
5
7
.
α
7
x
5
Obliczamy długo´s´c drugiej przyprostok ˛
atnej.
x
=
p
7
2
−
5
2
=
√
49
−
25
=
√
24
=
2
√
6.
W takim razie
tg α
=
5
x
=
5
2
√
6
=
5
√
6
12
.
Odpowied´z: C
Materiał pobrany z serwisu
9
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
21
(1
PKT
)
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry s ˛
a mniejsze od 5 jest
A) 17
B) 18
C) 19
D) 20
R
OZWI ˛
AZANIE
Pierwsz ˛
a cyfr˛e takiej liczby mo ˙zemy wybra´c na 4 sposoby (bo nie mo ˙ze to by´c 0). Drug ˛
a
cyfr˛e mo ˙zemy natomiast wybra´c na 5 sposobów. Razem daje nam to (zasada mno ˙zenia)
4
·
5
=
20
mo ˙zliwo´sci.
Odpowied´z: B
Z
ADANIE
22
(1
PKT
)
Dany jest okr ˛
ag o ´srodku S i promieniu r, długo´s´c łuku AB
=
1
4
·
2π
·
r (patrz rysunek).
α
A
B
S
Miara k ˛
ata α jest równa
A) 40
◦
B) 45
◦
C) 50
◦
D) 55
◦
R
OZWI ˛
AZANIE
Wiemy, ˙ze łuk AB ma długo´s´c równ ˛
a
1
4
·
2πr
2πr
=
1
4
długo´sci okr˛egu.
α
A
B
S 90
o
C
Materiał pobrany z serwisu
10

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Zatem k ˛
at ´srodkowy ]ASB ma miar˛e
1
4
·
360
◦
=
90
◦
.
K ˛
at wpisany ]ACB jest dwa razy mniejszy, czyli
α
=
]ACB
=
1
2
·
90
◦
=
45
◦
.
Odpowied´z: B
Z
ADANIE
23
(1
PKT
)
Z talii 52 kart wylosowano jedn ˛
a kart˛e. Jakie jest prawdopodobie ´nstwo, ˙ze wylosowano
pikow ˛
a dam˛e lub kierowego waleta?
A)
2
52
B)
4
52
C)
6
52
D)
8
52
R
OZWI ˛
AZANIE
Poniewa ˙z s ˛
a 2 zdarzenia sprzyjaj ˛
ace, prawdopodobie ´nstwo jest równe
2
52
.
Odpowied´z: A
Zadania otwarte
Z
ADANIE
24
(2
PKT
)
Wyka ˙z, ˙ze ci ˛
ag o wzorze ogólnym a
n
= −
2
+
14n, gdzie n > 1, jest ci ˛
agiem arytmetycznym.
R
OZWI ˛
AZANIE
Ci ˛
ag
(
a
n
)
jest ci ˛
agiem arytmetycznym je ˙zeli ró ˙znica a
n
+
1
−
a
n
mi˛edzy dwoma kolejnymi
wyrazami jest stała (tzn. nie zale ˙zy od n). Dla danego ci ˛
agu mamy
a
n
+
1
−
a
n
= −
2
+
14
(
n
+
1
) − (−
2
+
14n
) = −
2
+
14n
+
14
+
2
−
14n
=
14.
Jest to zatem ci ˛
ag arytmetyczny o ró ˙znicy 14.
Z
ADANIE
25
(2
PKT
)
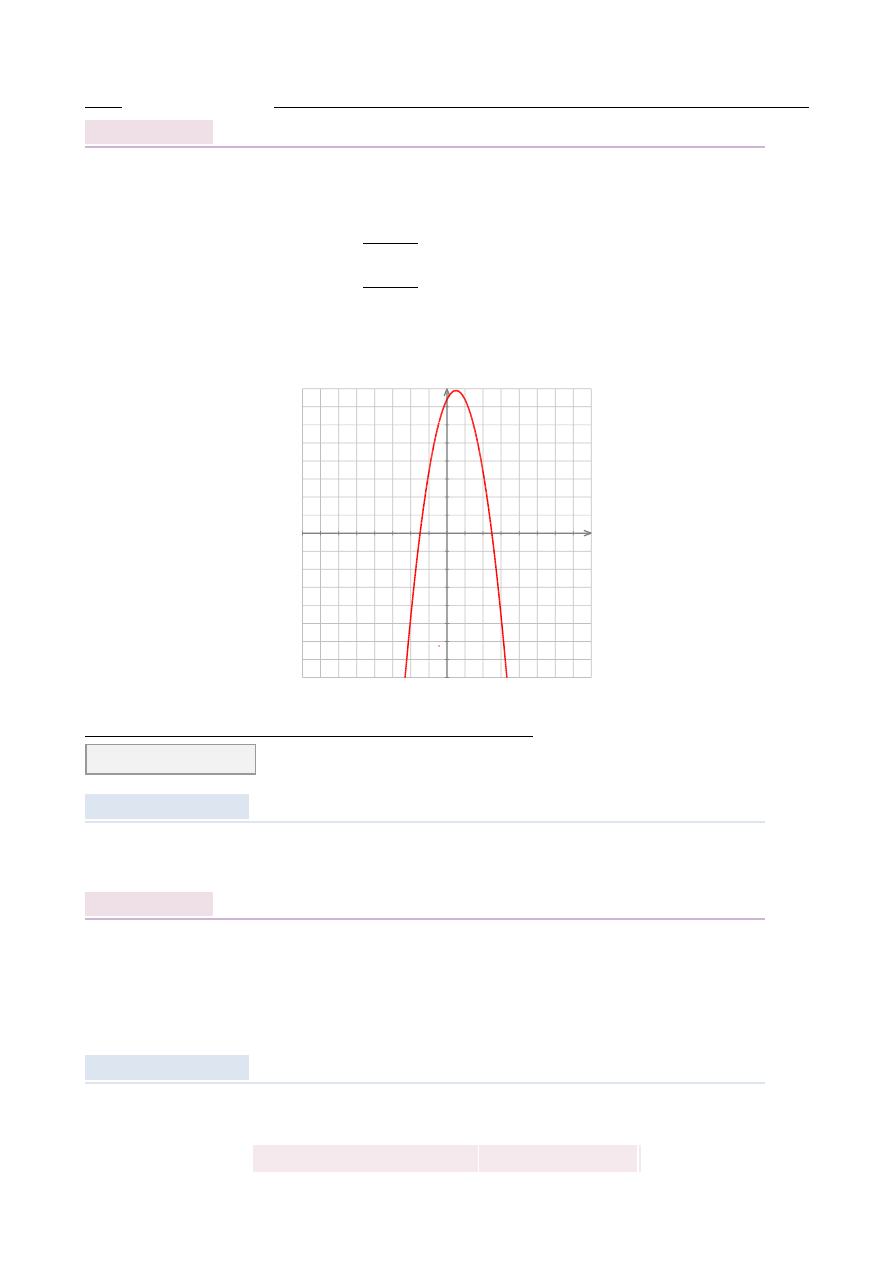
Dla jakich argumentów x, funkcja f
(
x
) = −
x
2
+
2x
+
15 przyjmuje warto´sci dodatnie?
Materiał pobrany z serwisu
11
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Znajdujemy najpierw miejsca zerowe trójmianu
−
x
2
+
2x
+
15
∆
=
2
2
+
4
·
1
·
15
=
4
+
60
=
64
x
1
=
−
2
−
8
−
2
=
5
x
2
=
−
2
+
8
−
2
= −
3.
Poniewa ˙z współczynnik przy x
2
jest ujemny, wykres tego trójmianu jest parabol ˛
a o ramio-
nach skierowanych w dół.
-10
-2
+2
+10
x
-10
-2
+2
+10
y
Otrzymujemy st ˛
ad rozwi ˛
azanie nierówno´sci:
(−
3, 5
)
.
Odpowied´z:
(−
3, 5
)
Z
ADANIE
26
(2
PKT
)
Wyka ˙z, ˙ze dla dowolnego k ˛
ata ostrego α, warto´s´c wyra ˙zenia sin
4
α
+
cos
2
α
+
sin
2
α
·
cos
2
α
jest stała.
R
OZWI ˛
AZANIE
Przekształcamy dane wyra ˙zenie korzystaj ˛
ac z jedynki trygonometrycznej.
sin
4
α
+
cos
2
α
+
sin
2
α
·
cos
2
α
=
=
sin
2
α
(
sin
2
α
+
cos
2
α
) +
cos
2
α
=
sin
2
α
+
cos
2
α
=
1.
Z
ADANIE
27
(2
PKT
)
Do´swiadczenie losowe polega na trzykrotnym rzucie symetryczn ˛
a monet ˛
a. Jakie jest praw-
dopodobie ´nstwo, ˙ze wylosujemy co najmniej dwa razy orła?
Materiał pobrany z serwisu
12
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Umówmy si˛e, ˙ze za wyniki uwa ˙zamy uporz ˛
adkowane ci ˛
agi otrzymanych reszek/orłów.
Mamy wtedy
|
Ω
3
| =
2
3
=
8.
Zdarzenia sprzyjaj ˛
ace to
(
O, O, R
)
,
(
O, R, O
)
,
(
R, O, O
)
,
(
O, O, O
)
i prawdopodobie ´nstwo wynosi
4
8
=
1
2
.
Odpowied´z:
1
2
Z
ADANIE
28
(2
PKT
)
Rozwi ˛
a ˙z równanie 0, 25 log
3
x
2
+
1
=
0.
R
OZWI ˛
AZANIE
Ze wzgl˛edu na dziedzin˛e logarytmu musi by´c oczywi´scie x
6=
0. Przekształcamy dane rów-
nanie.
0, 25 log
3
x
2
+
1
=
0
1
4
log
3
x
2
= −
1
/
·
4
log
3
x
2
= −
4
=
log
3
3
−
4
x
2
=
3
−
4
=
1
3
4
=
1
3
2
2
=
1
9
2
x
= ±
1
9
.
Odpowied´z: x
= −
1
9
lub x
=
1
9
Z
ADANIE
29
(4
PKT
)
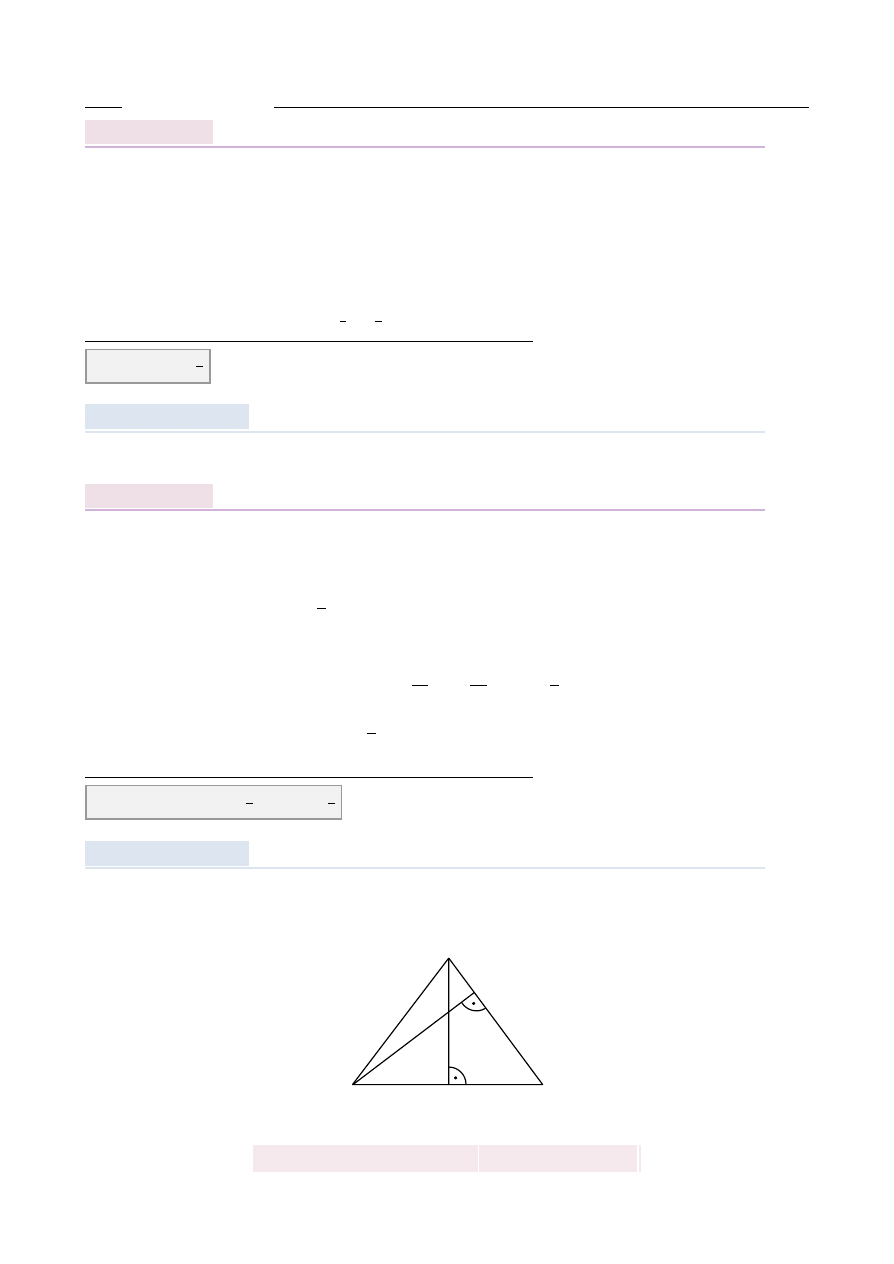
Oblicz pole trójk ˛
ata równoramiennego ABC (patrz rysunek,
|
AC
| = |
BC
|
), w którym wyso-
ko´s´c
|
AE
| =
8, a długo´s´c odcinka
|
BE
| =
6.
A
B
C
E
D
Materiał pobrany z serwisu
13

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
Korzystaj ˛
ac z twierdzenia Pitagorasa w trójk ˛
acie ABE obliczmy długo´s´c podstawy trójk ˛
ata
ABC.
AB
=
p
AE
2
+
BE
2
=
√
64
+
36
=
√
100
=
10.
W takim razie AD
=
DB
=
5. Wysoko´s´c DC obliczamy korzystaj ˛
ac z podobie ´nstwa trójk ˛
a-
tów ABE i CBD (oba s ˛
a prostok ˛
atne i maj ˛
a wspólny k ˛
at przy wierzchołku B).
AE
BE
=
CD
DB
8
6
=
CD
5
⇒
CD
=
8
6
·
5
=
40
6
=
20
3
.
Pole trójk ˛
ata ABC jest wi˛ec równe
1
2
AB
·
CD
=
1
2
·
10
·
20
3
=
100
3
.
Odpowied´z:
100
3
Z
ADANIE
30
(4
PKT
)
Dany jest prostok ˛
at o polu 72 cm
2
. Gdyby zwi˛ekszy´c długo´s´c jednego z boków o 2 cm, a
drugi bok zmniejszy´c o 3 cm, to pole nie ulegnie zmianie. Oblicz długo´sci boków danego
prostok ˛
ata.
R
OZWI ˛
AZANIE
Oznaczmy przez a i b długo´sci boków danego prostok ˛
ata. Wiemy, ˙ze
(
ab
=
72
(
a
+
2
)(
b
−
3
) =
72.
Podstawiamy b
=
72
a
z pierwszego równania do drugiego.
(
a
+
2
)
72
a
−
3
=
72
/
·
a
(
a
+
2
)(
72
−
3a
) =
72a
72a
−
3a
2
+
144
−
6a
=
72a
/ : 6
0
=
1
2
a
2
+
a
−
24
∆
=
1
+
48
=
49
a
= −
1
−
7
= −
8
∨
a
= −
1
+
7
=
6.
Ujemne rozwi ˛
azanie odrzucamy i mamy a
=
6. St ˛
ad b
=
72
a
=
12.
Odpowied´z: 6 cm i 12 cm.
Materiał pobrany z serwisu
14
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
31
(4
PKT
)
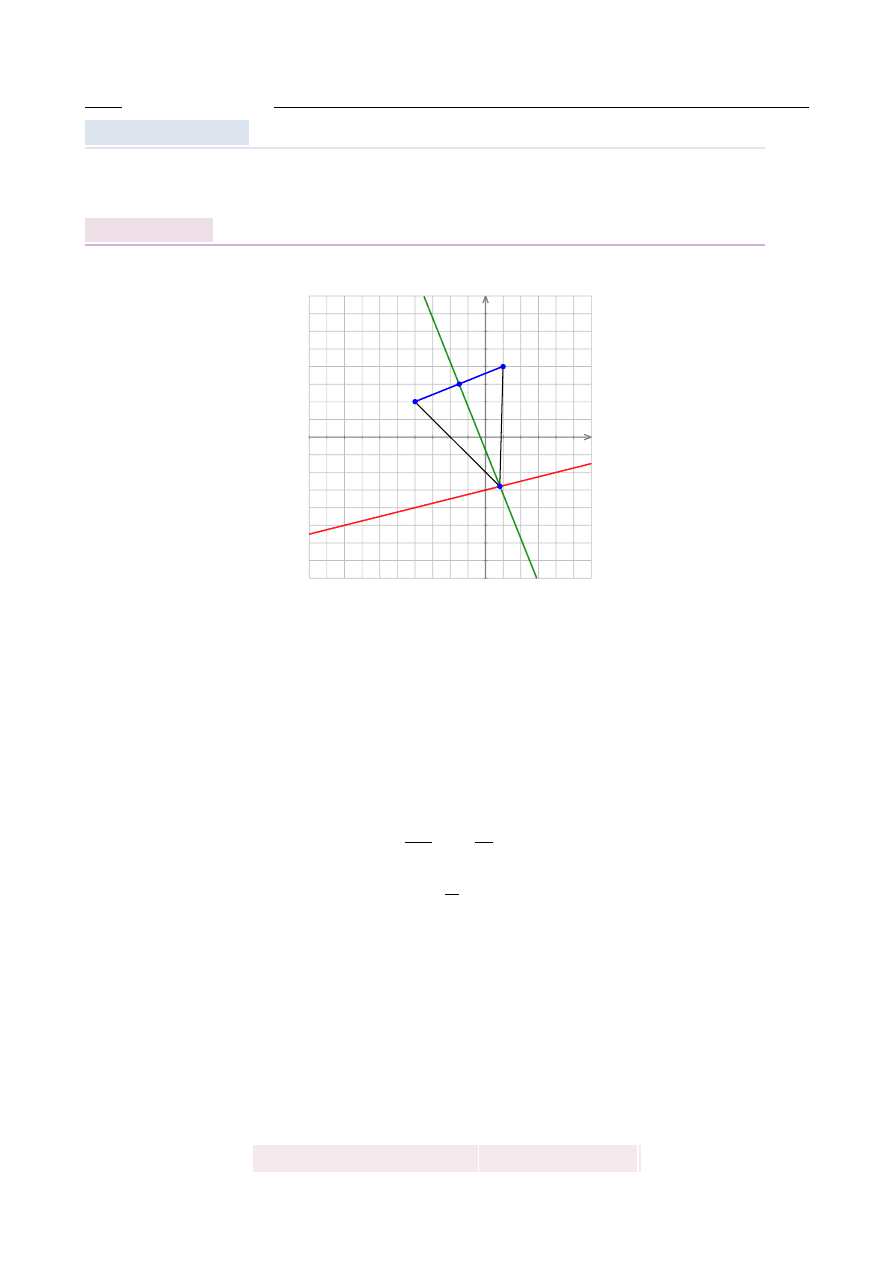
Dane s ˛
a dwa punkty A
= (−
4, 2
)
i B
= (
1, 4
)
oraz prosta k : x
+
4y
+
12
=
0. Wyznacz
współrz˛edne punktu C le ˙z ˛
acego na prostej k i tak samo odległego od punktów A i B.
R
OZWI ˛
AZANIE
Rozpoczynamy od szkicowego rysunku.
-10
-5
-1
+3
x
-5
-1
+1
+5
y
A
B
C
Sposób I
Szukamy punktu C
= (
x, y
) = (−
4y
−
12, y
)
tak, aby spełniona była równo´s´c AC
=
BC. Od
razu porównujemy kwadraty odległo´sci ( ˙zeby nie mie´c pierwiastków).
AC
2
=
BC
2
(−
4y
−
12
+
4
)
2
+ (
y
−
2
)
2
= (−
4y
−
12
−
1
)
2
+ (
y
−
4
)
2
(−
4y
−
8
)
2
+ (
y
−
2
)
2
= (−
4y
−
13
)
2
+ (
y
−
4
)
2
16y
2
+
64y
+
64
+
y
2
−
4y
+
4
=
16y
2
+
104y
+
169
+
y
2
−
8y
+
16
−
117
=
36y
⇒
y
= −
117
36
= −
13
4
.
St ˛
ad x
= −
4y
−
12
=
13
−
12
=
1 i C
=
1,
−
13
4
.
Sposób II
Tym razem napiszemy równanie symetralnej odcinka AB i znajdziemy jej punkt wspólny C
z dan ˛
a prost ˛
a x
+
4y
+
12
=
0.
Korzystamy ze wzoru na równanie prostej prostopadłej do wektora
→
v
= [
p, q
]
i przecho-
dz ˛
acej przez punkt
(
x
0
, y
0
)
p
(
x
−
x
0
) +
q
(
y
−
y
0
) =
0.
W naszej sytuacji mamy
→
v
=
−→
AB
= [
1
+
4, 4
−
2
] = [
5, 2
]
,
Materiał pobrany z serwisu
15

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
a punkt to ´srodek odcinka AB, czyli
−
4
+
1
2
,
2
+
4
2
=
−
3
2
, 3
.
W takim razie równanie symetralnej jest nast˛epuj ˛
ace
5
x
+
3
2
+
2
(
y
−
3
) =
0
/
·
2
10x
+
15
+
4y
−
12
=
0
4y
+
10x
+
3
=
0.
Szukamy teraz punktu wspólnego tej prostej z dan ˛
a prost ˛
a x
+
4y
+
12
=
0, czyli podsta-
wiamy w powy ˙zszym równaniu 4y
= −
x
−
12.
−
x
−
12
+
10x
+
3
=
0
9x
=
9
⇒
x
=
1.
Zatem y
=
1
4
(−
x
−
12
) = −
13
4
i C
=
1,
−
13
4
.
Odpowied´z: C
=
1,
−
13
4
Z
ADANIE
32
(5
PKT
)
Obj˛eto´s´c sto ˙zka jest równa 1000π, a tworz ˛
aca jest nachylona do podstawy pod k ˛
atem 30
◦
.
Oblicz pole powierzchni bocznej tego sto ˙zka.
R
OZWI ˛
AZANIE
Szkicujemy sto ˙zek.
h
r
r
30
o
l
Obliczamy wysoko´s´c i tworz ˛
ac ˛
a sto ˙zka w zale ˙zno´sci od promienia podstawy.
h
r
=
tg 30
◦
=
√
3
3
⇒
h
=
r
√
3
3
r
l
=
cos 30
◦
=
√
3
2
⇒
l
=
2r
√
3
.
Materiał pobrany z serwisu
16

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Wykorzystujemy teraz informacj˛e o obj˛eto´sci sto ˙zka.
1
3
πr
2
·
h
=
1000π
/ : π
1
3
r
2
·
r
√
3
3
=
1000
/
·
3
√
3
r
3
=
1000
·
3
√
3
= (
10
√
3
)
3
r
=
10
√
3.
Mamy zatem l
=
2r
√
3
=
20 i pole powierzchni bocznej sto ˙zka jest równe
P
b
=
πrl
=
π
·
10
√
3
·
20
=
200
√
3π.
Odpowied´z: 200
√
3π
Materiał pobrany z serwisu
17
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron