1
Mgr inż. Paweł Kossakowski
INSTRUKCJA NR 5
K
atedra
W
ytrzymałości
M
ateriałów
WYZNACZENIE SIŁY KRYTYCZNEJ
PRĘTA ŚCISKANEGO
1. WIADOMOŚCI WSTĘPNE
Wyboczenie pręta ściskanego pod wpływem działania siły osiowej jest jednym z przykładów
utraty stateczności układu sprężystego. W przypadku ściskania prętów stosunkowo krótkich
(pręty krępe) wymiary przekroju poprzecznego wyznacza się z warunku wytrzymałościowego
dop
A
N
σ
σ
<
=
. Natomiast wymiarowanie prętów smukłych przebiega z uwzględnieniem
smukłości. Zniszczenie pręta smukłego może nastąpić nie ze względu na przekroczenie jego
wytrzymałość na ściskanie, lecz na skutek zmiany jego kształtu i związanej z tym zmiany
charakteru stanu naprężenia – oprócz ściskania pojawi się zginanie, czyli naprężenia określać
będzie wzór
W
M
A
N +
=
σ
. Kształt osi pręta przy danej sile ściskającej – prostoliniowy lub
krzywoliniowy – zależy od rodzaju odpowiedniego stanu równowagi. Omówimy sobie to na
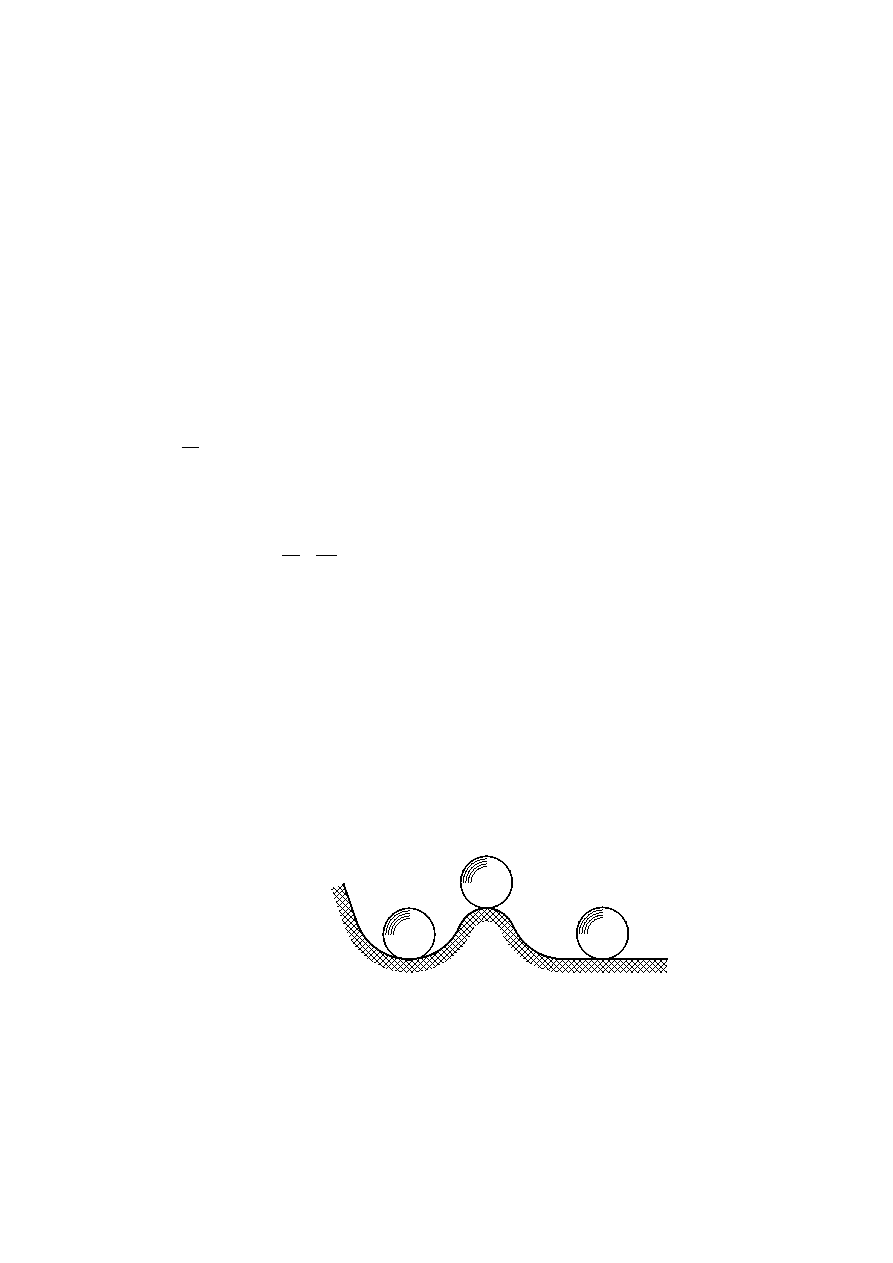
przykładzie ciężkiej kulki znajdującej się w 3 różnych położeniach (rys. 1). Dodanie kulce w
położeniu a) małej ilości energii spowoduje jej wahania około pierwszego położenia – do stanu
równowagi trwałej (statecznej). Wahania te na skutek sił tarcia po pewnym czasie wygasną.
Dowolnie mała ilość energii udzielona kulce w położeniu b) spowoduje przejście jej w inne
położenie równowagi. Kulka jest więc w stanie równowagi chwiejnej (niestatecznej). Natomiast
dodanie małej energii kulce w położeniu c) nie zmieni jej stanu równowagi – kulka jest więc w
stanie równowagi obojętnej.
Znamy zatem trzy rodzaje stanów równowagi układów mechanicznych:
- stan równowagi trwałej (statecznej) (rys. 1a)
- stan równowagi obojętnej (rys. 1b)
- stan równowagi chwiejnej (niestatecznej) (rys. 1c)
a)
b)
c)
Rys. 1 – Trzy rodzaje równowagi
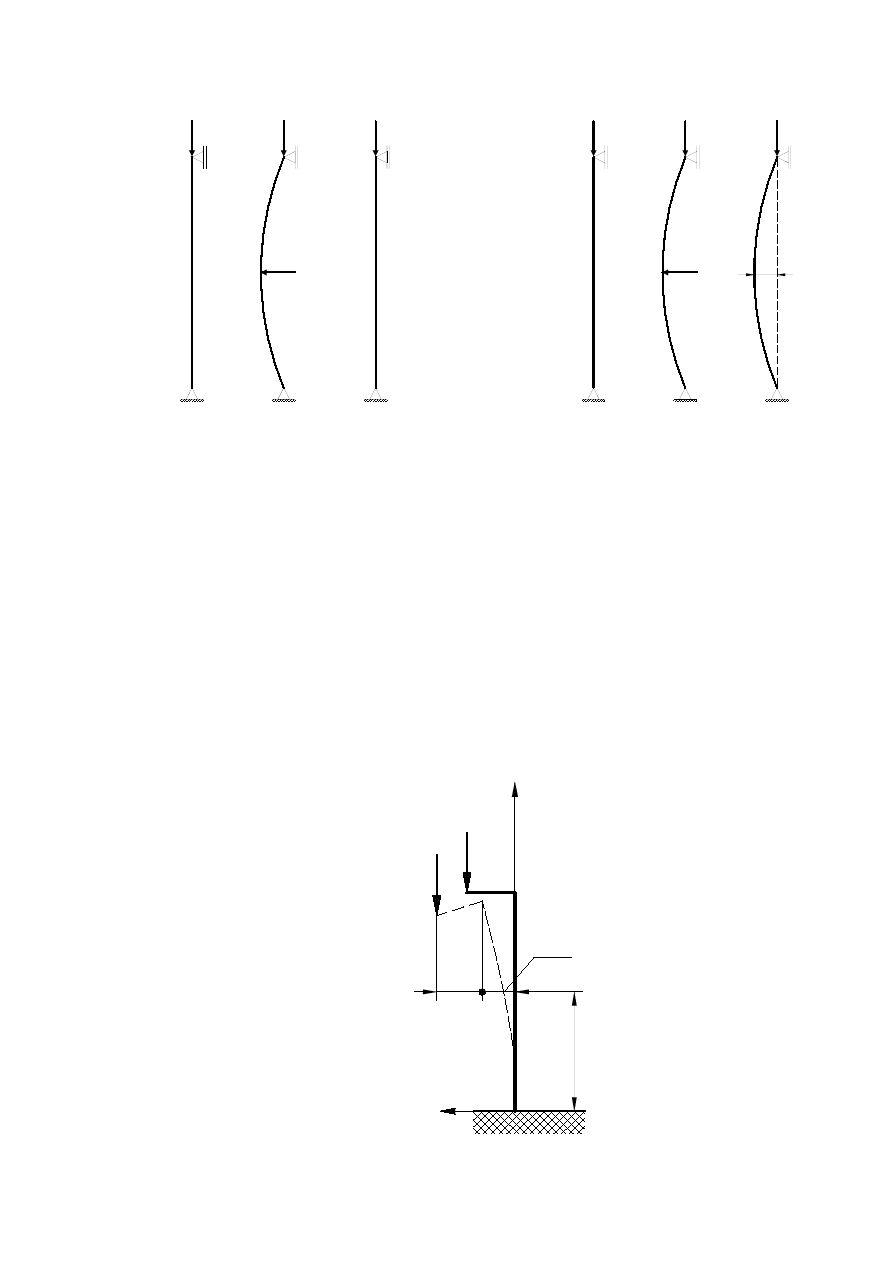
Przeanalizujmy teraz swobodnie podparty pręt obciążony siłą skupioną P równoległą do jego
osi. Jeśli siła ściskająca P jest mała, możliwa jest tylko postać równowagi trwałej. Pręt
wychylony z konfiguracji początkowej po odciążeniu do niej wraca. Jego równowaga będzie
trwała (stateczna) jeśli po jego wygięciu wskutek przyłożenia dowolnie małego czynnika
zakrzywiającego (np. siły
∆S prostopadłej do osi pręta) i po usunięciu tego czynnika pręt
wyprostuje się (powróci do sytuacji pierwotnej) – rys. 2.1.
2
P<P
a)
S
∆
kr
b)
kr
P<P
c)
P<P
kr
b)
∆
a)
P>P
kr
f
S
P>P
c)
P>P
kr
kr
Rys. 2.1 – Pręt obciążony siłą P < P
kr
Rys. 2.2 – Pręt obciążony siłą P > P
kr
Równowaga pręta będzie chwiejna (niestateczna), jeżeli po usunięciu chwilowego czynnika
zakrzywiającego pręt pozostanie nadal wygięty, a więc nie powróci do swej pierwotnej postaci,
natomiast nowa, zakrzywiona postać równowagi będzie natomiast trwała (stateczna) – rys.2.2.
Równowaga obojętna jest stanem rozgraniczającym równowagę stateczną i niestateczną.
Najmniejsza wartość siły P potrzebna do wyprowadzenia pręta ze stanu równowagi statecznej
do niestatecznej nosi miano siły krytycznej P
kr
.
Stan równowagi pręta ściskanego zależy od:
- siły ściskającej P
- długości pręta l
- sztywności giętej EJ
- warunków brzegowych (zamocowania)
W warunkach rzeczywistych, wykonanie idealnie prostego pręta i idealne przyłożenie
obciążenia P nie jest możliwe. Dlatego też zawsze istnieje pewien mimośród obciążenia e.
Rozważmy pręt pokazany na rys. 3.
z
A
B'
B
x
x
f
B
w(x)
P
P
e
Rys. 3 – Pręt rzeczywisty
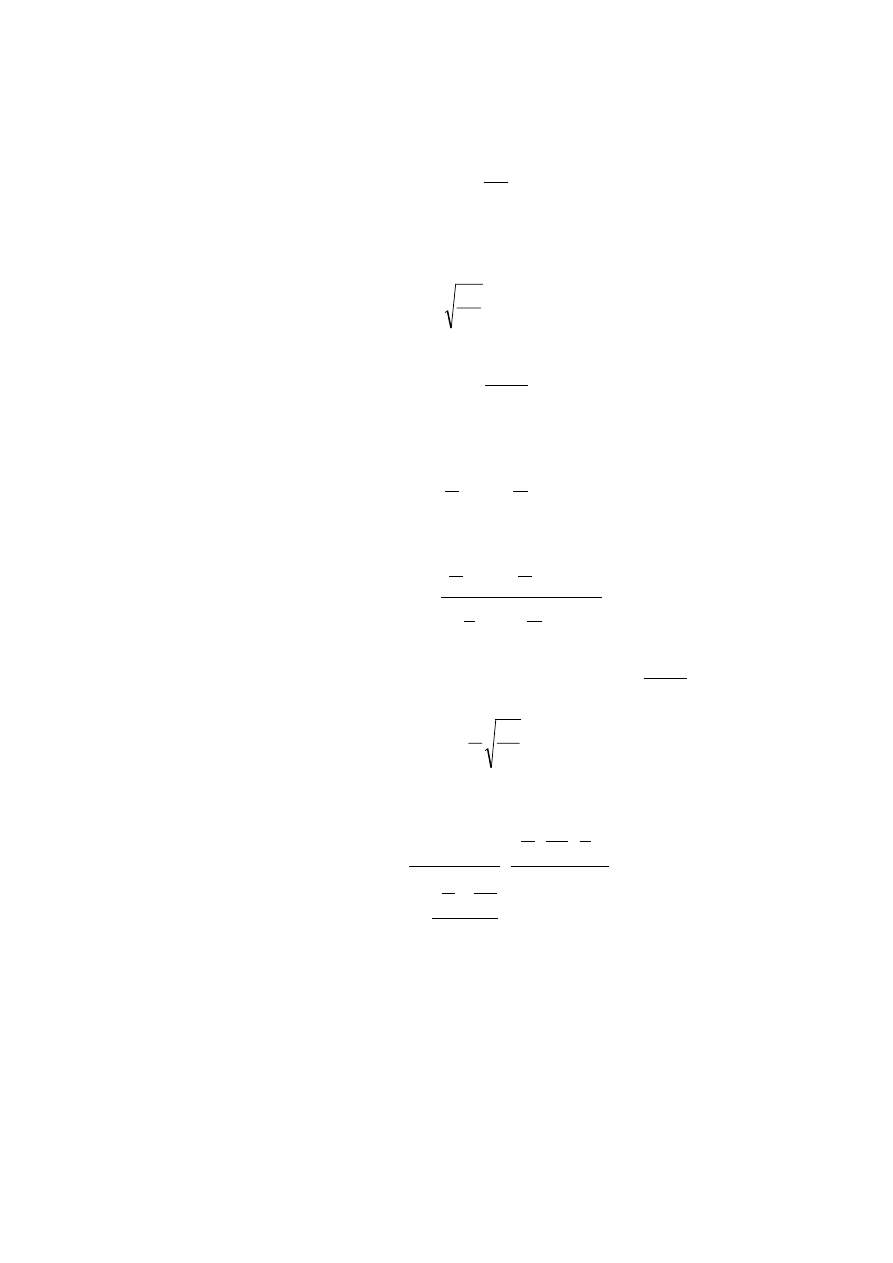
3
Moment gnący w dowolnym punkcie pręta wyraża się wzorem:
( )
[
]
x
w
f
e
P
M
B
−
+
=
(1)
EJ
M
w
=
''
(2)
Podstawiając (1) do (2) dochodzimy do równania:
[
]
B
f
e
k
w
k
w
+
=
+
2
2
''
(3)
gdzie:
EJ
P
k
=
którego rozwiązanie dla warunków brzegowych widocznych na rys. 3 przyjmuje postać:
( ) ( )
(
)
kx
kl
e
x
P
w
x
k
w
cos
1
cos
,
,
−
=
=
(4)
W celu wyznaczenia wartości siły krytycznej P
kr
należy funkcję cos(x) rozwinąć w szereg
Maclaurina:
( )
( )
...
!
4
1
!
2
1
1
cos
4
2
−
+
−
=
kx
kx
kx
(5)
Wzór (4) przybiera więc postać:
( )
( )
( )
( )
( )
..
!
4
1
2
1
1
..
!
4
1
!
2
1
,
4
2
4
2
−
+
−
−
+
⋅
=
kl
kl
kx
kx
e
x
P
w
(6)
Wyrażając składnik kl za pomocą eulerowskiej siły krytycznej
( )
2
2
2l
EJ
P
kr
π
=
otrzymujemy:
kr
P
P
kl
2
π
=
(7)
Dla drugiego przybliżenia szeregu (5) przemieszczenie pręta w dowolnym punkcie wynosi:
( )
−
=
2
2
2
2
1
,
2
2
l
x
P
P
P
P
e
x
P
w
kr
kr
π
π
(8)
2. WYKONANIE ĆWICZENIA
2.1 Cel ćwiczenia
Celem ćwiczenia jest eksperymentalne wyznaczenie siły krytycznej P
kr
metodą
Southwella dla
kilku różnych wielkości mimośrodu obciążenia.
2.2 Stanowisko pomiarowe
Pręt 1 (rys. 4), dla którego wyznaczamy siłę krytyczną jest utwierdzony u dołu, u góry zaś –
obciążony siłą P przyłożoną na zmiennym mimośrodzie e. Siłę P przykłada się obciążając szalkę
ciężarkami 2. Pręt wraz z podporą 3 można nachylać uzyskując wymuszenia w
0
(x) za pomocą

4
składowej prostopadłej do osi pręta. Ugięcia w mierzone są za pomocą czujnika zegarowego 4.
Widok stanowiska przedstawia fot. 1.
α
3
4
P
2
x
0
l
1
Rys. 4 – Schemat stanowiska pomiarowego.
Fot. 1 – Widok stanowiska pomiarowego.
2.3 Przebieg ćwiczenia
Na stanowisku mierzymy
(
)
0
, x
P
w
w punkcie
2
/
0
l
x
=
dla różnych wartości obciążenia P.
Z zależności (8) otrzymujemy:
(
)
kr
kr
kr
kr
P
P
P
P
e
l
x
P
P
P
P
e
x
P
w
32
8
1
2
2
2
2
1
,
2
2
2
0
2
2
0
π
π
π
π
⋅
−
=
−
=
(9)
Przyjmując
1
8
2
≅
π
otrzymujemy zależność:
(
)
(
)
const
e
x
P
w
P
x
P
w
P
kr
=
=
−
4
1
,
,
0
0
(10)
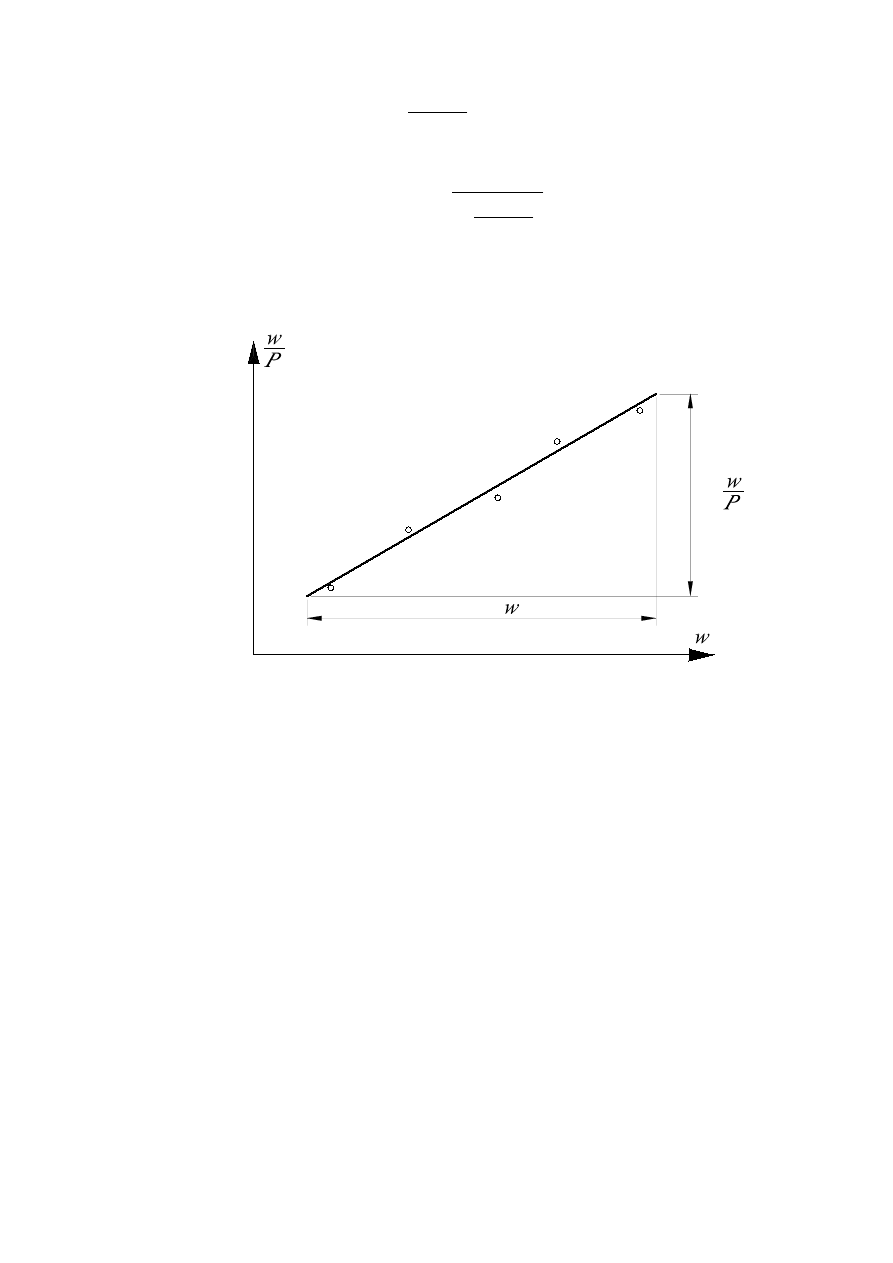
5
która w układzie współrzędnych
(
) ( )
0
0
,
,
,
x
P
w
P
x
P
w
przedstawia linię prostą (rys. 5). Siła
kr
P
jest więc związana z nachyleniem tej prostej i można ją wyznaczyć z zależności:
(
)
(
)
∆
∆
=
P
x
P
w
x
P
w
P
kr
0
0
,
,
(11)
Wzór (11) łączy się z nazwiskiem Southwella i stąd nazwa sposobu doświadczalnego
wyznaczania siły krytycznej.
∆
( )
∆
Rys. 5 – Wykres Southwella
Przed przystąpieniem do wykonania ćwiczenia należy zmierzyć długość pręta oraz wymiary
jego przekroju poprzecznego niezbędne do wyznaczenia momentu bezwładności. Pomiary
wartości, na których bazie będzie potem wyznaczana siła krytyczna, przeprowadzamy dla trzech
wartości mimośrodu e i trzech wartości obciążenia P dla każdego mimośrodu. Przyjmujemy, że
podpora 3 jest ustawiona poziomo.
2.4. Wykonanie sprawozdania.
Sprawozdanie powinno zawierać:
1/ Cel ćwiczenia.
2/ Wprowadzenie teoretyczne.
3/ Schemat stanowiska pomiarowego.
4/ Tabelę z wynikami pomiarów.
5/ Obliczenia oraz ich analizę.
6/ Wyznaczoną średnią wartość obciążenia krytycznego pręta.
7/ Wartość obciążenia krytycznego wyznaczoną teoretycznie.
8/ Wnioski.
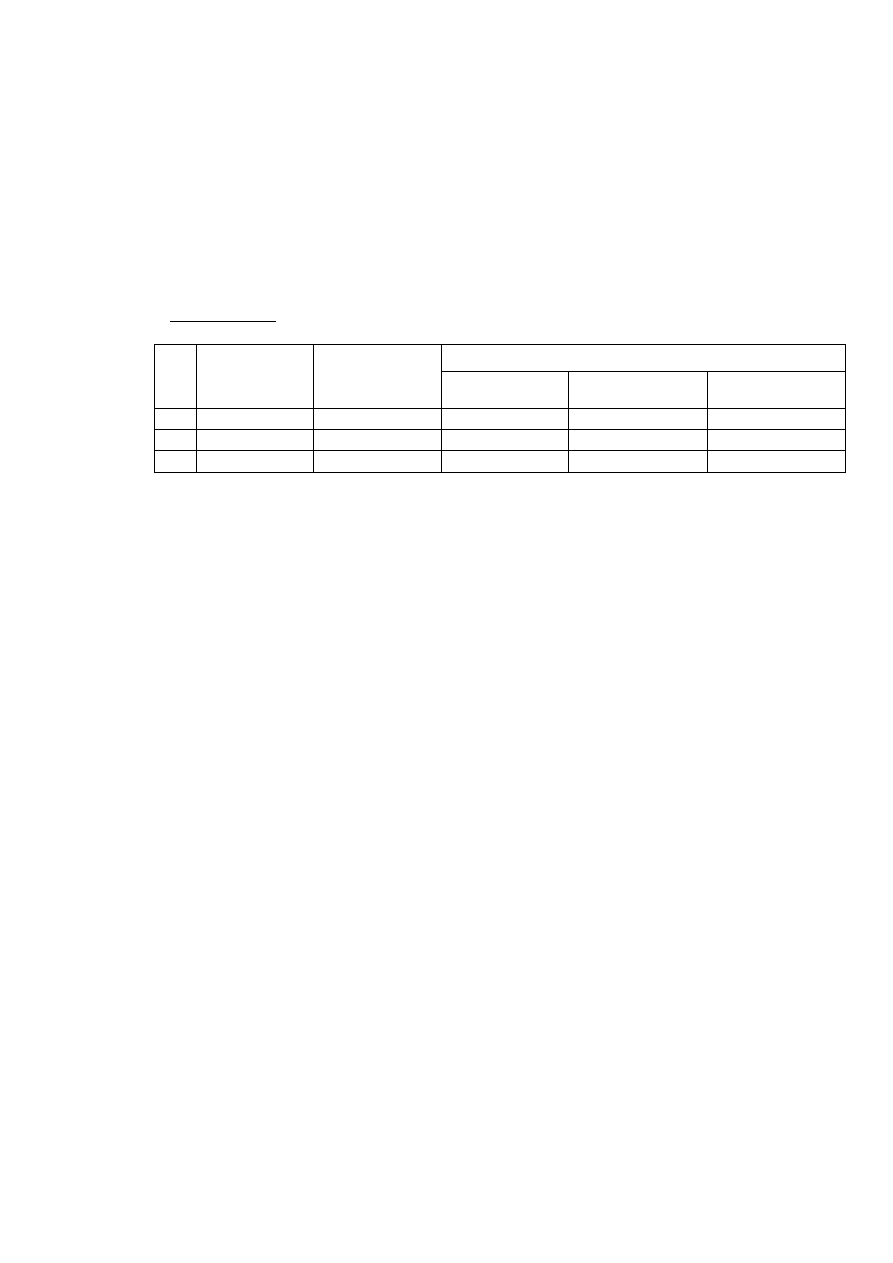
6
Tabela i wzór protokołu sprawozdania
WYZNACZENIE SIŁY KRYTYCZNEJ PRĘTA ŚCISKANEGO
Protokół nr ……………
Materiał pręta ……………
Wymiary przekroju pręta …………
Moment bezwładności przekroju pręta ………………
Tabela pomiarów
Wskazania czujników dla obciążenia [mm]
L.p.
Mimośród
e
[mm]
Stan początkowy
czujnika
[mm]
( )
1
P
w
( )
2
P
w
( )
3
P
w
1
2
3
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron