Trí tuệ nhân tạo

Chương 1

MỞ ĐẦU

1.1. Tổng quan về khoa học trí tuệ nhân tạo

Trong CNTT, Trí Tuệ Nhân Tạo (Artificial Intelligence) là một ngành

mới, nhưng phát triển rất mạnh mẽ và đem lại nhiều kết quả to lớn. Con người
thường tự cho mình là sinh vật thông minh vì khả năng trí tuệ đóng vai trò quan
trong trong cuộc sống. Trong văn học cũng đã từng có những câu chuyện đề cao
về trí thông minh của con người.

Trí Tuệ Nhân Tạo chỉ mới hình thành từ năm 1956. Tuy nhiên, việc

nghiên cứu trí tuệ đã có từ lâu. Trên 2000 năm trước, các nhà triết học đã tìm
hiểu về cách thức nhìn nhận, học tập, nhớ và suy lý. Việc ra đời của máy tính
điện tử vào những năm 50 của thế kỷ 20 đã sinh ra khuynh hướng đưa các lĩnh
vực nghiên cứu trí tuệ về các vấn đề lý thuyết và thực nghiệm trên máy.

1.1.1. Đối tượng và mục tiêu nghiên cứu của trí tuệ nhân tạo

+ Đối tượng nghiên cứu: Trí tuệ nhân tạo nghiên cứu về cách hành xử

(hay cơ chế của các hành vi) thông minh (intelligent behaviour) ở người và
máy.

+ Mục tiêu: Xây dựng lý thuyết đầy đủ về thông minh để có thể giải thích

được hoạt động thông minh của sinh vật và áp dụng được các hiểu biết vào các
máy móc nói chung, nhằm phục vụ cho con người. (Hay nói cách khác tạo chiếc
máy tính có khả năng nhận thức, suy luận và phản ứng).

* Thế nào là máy thông minh?

Là máy vượt qua được thử nghiệm (trắc nghiệm) Turing.

* Trắc nghiệm Turing (Turing test):

Năm 1950, một nhà toán học người Anh là Alan Turing đã viết những

trang sách đầu tiên trả lời một cách cụ thể câu hỏi: trí tuệ máy có liên hệ như thế
nào với máy tính kỹ thuật số hiện đại? Liệu có thể làm cho một máy tính thực
sự có khả năng suy nghĩ hay không?

Trí tuệ nhân tạo

Để giải quyết những mơ hồ trong câu hỏi này, ông đã đề xuất thay thế câu

trả lời bằng kết quả của một trắc nghiệm mang tính thực nghiệm - trắc nghiệm
Turing (Turing test) hay “trò chơi bắt chước”.

Hình 1.1. Trắc nghiệm Turing

Trong trắc nghiệm này: một máy tính và một người tham gia trắc nghiệm

được đặt vào trong các căn phòng cách biệt với một người thứ hai (người thẩm
vấn). Người thẩm vấn không biết được chính xác đối tượng nào là người hay
máy tính, và cũng chỉ có thể giao tiếp với hai đối tượng đó thông qua các
phương tiện kỹ thuật như một thiết bị soạn thảo văn bản, hay thiết bị đầu cuối.

Người thẩm vấn có nhiệm vụ phân biệt người với máy tính bằng cách chỉ

dựa trên những câu trả lời của họ đối với những câu hỏi được truyền qua thiết bị
liên lạc này.

Trong trường hợp nếu người thẩm vấn không thể phân biệt được máy tính

với người (tức không cần ràng buộc máy làm gì, như thế nào miễn là máy đó
làm cho người thẩm vấn tưởng máy là người) thì khi đó, theo Turing, máy tính
này có thể được xem là thông minh.

* Ưu điểm của trắc nghiệm Turing:

Nó đưa ra một khái niệm khách quan về trí tuệ, tức là hành vi của một

thực thể thông minh nào đó đáp ứng lại một tập hợp các câu hỏi đặc thù. Việc
này cho chúng ta một chuẩn mực để xác định trí thông minh.

Nó tránh cho chúng ta khỏi bị lạc đường bởi những câu hỏi rắc rối và

hiện thời chưa thể trả lời được, chẳng hạn như máy tính có sử dụng những suy

Trí tuệ nhân tạo

luận thích hợp bên trong nó hay không? hay máy tính thực sự có ý thức được
những hành động của nó hay không?

Nó loại trừ bất cứ định kiến thiên vị nào vì bắt buộc người thẩm vấn chỉ

tập trung vào nội dung các câu trả lời.

* Như vậy::

- Về mặt kỹ thuật: Tạo ra các máy thông minh để giải quyết vấn đề thực

tế dùng các kỹ thuật AI.

- Khoa học: Phát triển các khái niệm và thuật ngữ để hiểu được các hành

xử thông minh của sinh vật.

1.1.2. Vai trò của trí tuệ nhân tạo

Trí tuệ nhân tạo bao quát rất nhiều lĩnh vực nghiên cứu hẹp. Nó nghiên

cứu từ các lĩnh vực tổng quát như máy nhận biết, suy luận logic, đến các bài
toán như chơi cờ, chứng minh định lý. Thường thì các nhà khoa học ở các lĩnh
vực khác tìm đến với trí tuệ nhân tạo ở các kỹ thuật hệ thống hoá và tự động hoá
các xử lý tri thức cũng như các phương pháp thuộc lĩnh vực mang tính người.

Trí tuệ nhân tạo nghiên cứu kỹ thuật làm cho máy tính có thể “suy nghĩ

một cách thông minh” và mô phỏng quá trình suy nghĩ của con người khi đưa ra
những quyết định, lời giải. Trên cơ sở đó, thiết kế các chương trình cho máy
tính để giải quyết bài toán.

Sự ra đời và phát triển của Trí tuệ nhân tạo đã tạo ra một bước nhảy vọt

về chất trong kỹ thuật và kỹ nghệ xử lý thông tin. Trí tuệ nhân tạo chính là cơ sở
của công nghệ xử lý thông tin mới, độc lập với công nghệ xử lý thông tin truyền
thống dựa trên văn bản giấy tờ. Điều này được thể hiện qua các mặt sau:

- Nhờ những công cụ hình thức hoá (các mô hinh logic ngôn ngữ, logic

mờ,...), các tri thức thủ tục và tri thức mô tả có thể biểu diễn được trong máy.
Do vậy quá trình giải bài toán được tiến hành hữu hiệu hơn.

- Mô hình logic ngôn ngữ đã mở rộng khả năng ứng dụng của máy tính

trong lĩnh vực đòi hỏi tri thức chuyên gia ở trình độ cao, rất khó như: y học,
sinh học, địa lý, tự động hóa.

Trí tuệ nhân tạo

- Một số phần mềm trí tuệ nhân tạo thể hiện tính thích nghi và tính mềm

dẻo đối với các lớp bài toán thuộc nhiều lĩnh vực khác nhau.

- Khi máy tính được trang bị các phần mềm trí tuệ nhân tạo ghép mạng sẽ

cho phép giải quyết những bài toán cỡ lớn và phân tán.

So sánh kỹ thuật lập trình truyền thống và kỹ thuật xử lý tri thức

trong TTNT

Truyền thống

TTNT

Xử lý dữ liệu

Xử lý tri thức

Xử lý theo các thuật toán

Xử lý theo các thuật giải Heuristics

Xử lý tuần tự theo lô

Xử lý theo chế độ tương tác cao (ngôn ngữ tự
nhiên, có giao tiếp với bên ngoài)

Không giải thích trong quá trình
thực hiện

Có thể giải thích hành vi hệ thống trong quá
trình thực hiện

1.1.3. Các kỹ thuật trí tuệ nhân tạo

Có nhiều kỹ thuật nghiên cứu, phát triển ngành khoa học Trí tuệ nhân tạo.

Tuy vậy, các kỹ thuật Trí tuệ nhân tạo thường khá phức tạp khi cài đặt cụ thể, lý
do là các kỹ thuật này thiên về xử lý các ký hiệu tượng trưng và đòi hỏi phải sử
dụng những tri thức chuyên môn thuộc nhiều lĩnh vực khác nhau.

Do vậy, các kỹ thuật Trí tuệ nhân tạo hướng tới khai thác những tri thức

về lĩnh vực đang quan tâm được mã hoá trong máy sao cho đạt được mức độ
tổng quát; dễ hiểu, dễ diễn đạt thông qua ngôn ngữ chuyên môn gần gũi với
ngôn ngữ tự nhiên; dễ sửa đổi, hiệu chỉnh, dễ sử dụng, khai thác nhằm thu hẹp
các khả năng cần xét để đi tới lời giải cuối cùng.

* Các kỹ thuật Trí tuệ nhân tạo cơ bản bao gồm :

- Lý thuyết giải bài toán và suy diễn thông minh: Lý thuyết giải bài

toán cho phép viết các chương trình giải câu đố, chơi các trò chơi thông qua các
suy luận mang tính người; các hệ thống chứng minh định lý. Ngoài ra các hệ
thống hỏi đáp thông minh còn cho phép lưu trữ và xử lý khối lượng lớn các
thông tin.

Trí tuệ nhân tạo

- Lý thuyết tìm kiếm may rủi: Lý thuyết này bao gồm các phương pháp

và kỹ thuật tìm kiếm với sự hỗ trợ của thông tin phụ để giải bài toán một cách
có hiệu quả.

- Các ngôn ngữ về Trí tuệ nhân tạo: Để xử lý các tri thức người ta

không chỉ sử dụng các ngôn ngữ lập trình dùng cho các xử lý dữ liệu số, mà cần
có ngôn ngữ khác. Các ngôn ngữ chuyên dụng này cho phép lưu trữ và xử lý
thông tin ký hiệu. Một số ngôn ngữ được nhiều người biết đến là IPL.V,LISP,
PROLOG.

- Lý thuyết thể hiện tri thức và hệ chuyên gia: Trí tuệ nhân tạo là khoa

học về thể hiện và sử dụng tri thức. Mạng ngữ nghĩa, lược đồ, logic vị từ, khung
là các phương pháp thể hiện tri thức thông dụng. Việc gắn liền cách thể hiện và
sử dụng tri thức là cơ sở hình thành hệ chuyên gia.

- Lý thuyết nhận dạng và xử lý tiếng nói: Giai đoạn phát triển đầu của

Trí tuệ nhân tạo gắn với lý thuyết nhận dạng. Các phương pháp nhận dạng chính
gồm: nhận dạng hình học, nhận dạng dùng tâm lý học, nhận dạng theo phương
pháp hàm thế, dùng máy nhận dạng. ứng dụng của phương pháp này trong việc
nhận dạng chữ viết, âm thanh.

- Người máy: Cuối những năm 70, người máy trong công nghiệp đã đạt

được nhiều tiến bộ. Người máy có bộ phận cảm nhận và các cơ chế hoạt động
được nối ghép theo sự điều khiển thông minh. Khoa học về cơ học và Trí tuệ
nhân tạo được tích hợp trong khoa học người máy.

- Tâm lý học xử lý thông tin : Các kết quả nghiên cứu của tâm lý học

giúp Trí tuệ nhân tạo xây dựng các cơ chế trả lời theo hành vi, có ý thức; nó
giúp cho việc thực hiện các suy diễn mang tính người.

- Ngoài ra, xử lý danh sách, kỹ thuật đệ quy, kỹ thuật quay lui và xử

lý cú pháp hình thức là những kỹ thuật cơ bản của tin học truyền thống có liên
quan trực tiếp đến Trí tuệ nhân tạo.

1.2. Lịch sử phát triển của trí tuệ nhân tạo

Lịch sử của Trí tuệ nhân tạo cho thấy ngành khoa học này có nhiều kết

quả đáng ghi nhận. Theo các mốc phát triển, người ta thấy Trí tuệ nhân tạo được
sinh ra từ những năm 50 với các sự kiện sau:

Trí tuệ nhân tạo

•

Turing được coi là người khai sinh ngành Trí tuệ nhân tạo bởi phát

hiện của ông về máy tính có thể lưu trữ chương trình và dữ liệu.

•

Tháng 8/1956 J.Mc Carthy, M. Minsky, A. Newell, Shannon.

Simon ,… đưa ra khái niêm “trí tuệ nhân tạo”.

•

Vào khoảng năm 1960 tại Đại học MIT (Massachussets Institure of

Technology) ngôn ngữ LISP ra đời, phù hợp với các nhu cầu xử lý đặc
trưng của trí tuệ nhân tạo - đó là ngôn ngữ lập trình đầu tiên dùng cho trí
tuệ nhân tạo.

•

Thuật ngữ Trí tuệ nhân tạo được dùng đầu tiên vào năm 1961 cũng

tại MIT.

•

Những năm 60 là giai đoạn lạc quan cao độ về khả năng làm cho

máy tính biết suy nghĩ. Trong giai đoạn này người ta đã được chứng kiến
máy chơi cờ đầu tiên và các chương trình chứng minh định lý tự động.

Cụ thể:

1961: Chương trình tính tích phân bất định

1963: Các chương trình Heuristics: Chương trình chứng minh các

định lý hình học không gian có tên là “tương tự”, chương trình chơi cờ của
Samuel.

1964: Chương trình giải phương trình đại số sơ cấp, chương trình

trợ giúp ELIZA (có khả năng làm việc giống như một chuyên gia phân tich tâm
lý).

1966: Chương trình phân tích và tổng hợp tiếng nói

1968: Chương trình điều khiển người máy (Robot) theo đồ án “Mắt

– tay”, chương trình học nói.

•

Vào những năm 60, do giới hạn khả năng của các thiết bị, bộ nhớ

và đặc biệt là yếu tố thời gian thực hiện nên có sự khó khăn trong việc
tổng quát hoá các kết quả cụ thể vào trong một chương trình mềm dẻo
thông minh.

•

Vào những năm 70, máy tính với bộ nhớ lớn và tốc độ tính toán

nhanh nhưng các phương pháp tiếp cận Trí tuệ nhân tạo cũ vẫn thất bại
(do sự bùng nổ tổ hợp trong quá trình tìm kiếm lời giải các bài toán đặt
ra).

Trí tuệ nhân tạo

•

Vào cuối những năm 70 một vài kết quả như xử lý ngôn ngữ tự

nhiên, biểu diễn tri thức và giải quyết vấn đề. Những kết quả đó đã tạo
điều kiện cho sản phẩm thương mại đầu tiên của Trí tuệ nhân tạo ra đời
đó là Hệ chuyên gia, được đem áp dụng trong các lĩnh vực khác nhau
(Hệ chuyên gia là một phần mềm máy tính chứa các thông tin và tri thức
về một lĩnh vực cụ thể nào đó, có khả năng giải quyết những yêu cầu của
người sử dụng trong một mức độ nào đó, ở một trình độ như một chuyên
gia con người có kinh nghiệm khá lâu năm).

•

Một sự kiện quan trọng vào những năm 70 là sự ra đời ngôn ngữ

Prolog, tương tự LISP nhưng nó có cơ sở dữ liệu đi kèm.

•

Vào những năm 80, thị trường các sản phẩm dân dụng đã có khá

nhiều sản phẩm ở trình đô cao như: máy giặt, máy ảnh,... sử dụng Trí tuệ
nhân tạo. Các hệ thống nhận dạng và xử lý ảnh, tiếng nói.

•

Những năm 90, các nghiên cứu nhằm vào cài đặt thành phần thông

minh trong các hệ thống thông tin, gọi chung là cài đặt trí tuệ nhân tạo,
làm rõ hơn các ngành của khoa học Trí tuệ nhân tạo và tiến hành các
nghiên cứu mới, đặc biệt là nghiên cứu về cơ chế suy lý, về Trí tuệ nhân
tạo phân tạo, về các mô hình tương tác.

* Những đặc trưng của Trí tuệ nhân tạo

•

Trí tuệ nhân tạo xử lý thông tin theo trật tự ký hiệu. Các thông tin

gồm: khái niệm, luật, các đối tượng ? dùng cho suy lý. Khái niệm cơ bản
trong Trí tuệ nhân tạo là sự thể hiện, suy lý, nhận biết, việc học và hệ
thống cơ sở tri thức.

•

Phương pháp may rủi hay được dùng trong Trí tuệ nhân tạo.

Phương pháp này cho phép giải hai lớp bài toán khó. Thứ nhất là những
bài toán chưa có thuật giải ( bài toán nhận biết, ra quyết định). Thứ hai là
các bài toán đã có thuật giải nhưng độ phức tạp lớn ( chẳng hạn bài toán
chơi cờ).

•

Trí tuệ nhân tạo xét đến những thông tin không đầy đủ, không

chính xác, có vẻ mâu thuẫn. Tuy vậy, các kết quả của Trí tuệ nhân tạo là
cụ thể.

•

Việc tương tác người- máy đi đôi với nhận biết tự động là cần thiết

trong Trí tuệ nhân tạo. Các bài toán nhận dạng là ví dụ về yêu cầu này.

Trí tuệ nhân tạo

•

Trí tuệ nhân tạo liên quan đến nhiều lĩnh vực, như các kỹ thuật

mới, logic học, khoa học nhận biết, ngôn ngữ học, khoa học về tổ chức,
thần kinh học. Trí tuệ nhân tạo còn nằm trong các lĩnh vực nghiên cứu
nâng cao, các đề án nghiên cứu quan trọng.

1.3. Một số vấn đề trí tuệ nhân tạo quan tâm

1.3.1. Những vấn đề chung

Khoa học Trí tuệ nhân tạo liên quan đến cảm giác, tri giác và cả quá trình

tư duy thông qua các hành vi, giao tiếp. Nó có các định hướng nghiên cứu, ứng
dụng sau:

- Tìm và nghiên cứu các thủ tục giúp con người tiến hành các hoạt động

sáng tạo. Công việc sáng tạo được thực hiện trên mô hình theo cấu trúc, chức
năng và sử dụng công nghệ thông tin.

- Dùng ngôn ngữ tự nhiên. Trước hết là ngôn ngữ được dùng để thể hiện

tri thức, tiếp thu và chuyển hoá sang dạng có thể xử lý được.

- Hình thức hoá các khía cạnh, các hành vi liên quan đến Trí tuệ nhân tạo.

Do vậy có thể xây dựng các bài toán mang tính người và thông minh.

Các hoạt động lớn trong Trí tuệ nhân tạo bao gồm: chứng minh định lý,

xử lý ngôn ngữ tự nhiên, hiểu tiếng nói, phân tích ảnh và hình, người máy và hệ
chuyên gia. Về cài đặt hệ thống, khuynh hướng hiện tại của Trí tuệ nhân tạo là
cài đặt các hệ Trí tuệ nhân tạo trong các hệ thống khác, đặc biệt là trong các hệ
thống tin học.

1.3.2. Những vấn đề chưa được giải quyết trong trí tuệ nhân tạo

Những thành tựu nghiên cứu và ứng dụng các kỹ thuật Trí tuệ nhân tạo đã

khẳng định tính thực tiễn của các dự án xây dựng máy tính có khả năng suy
nghĩ. Tuy vậy trong một số phạm vi, máy tính còn thua xa so với hoạt động
của hệ thần kinh con người:

Sự khác nhau trong hoạt động giữa máy tính và bộ não con người, điều

này thể hiện ưu thế của máy tính so với bộ não người vì khả năng tính toán rất
lớn (nhất là trong các chương trình xử lý dữ liệu lớn).

Trí tuệ nhân tạo

Xử lý song song: mặc dù công nghệ điện tử hiện đại cho phép xây dựng

các bộ đa xử lý, song máy tính không thể hoạt động song song như bộ não con
người được.

Khả năng diễn giải: con người có thể xem xét cùng một vấn đề theo

những phương pháp khác nhau, từ đó diễn giải theo cách dễ hiểu nhất. Ngược
lại, sự linh hoạt này không thể mô phỏng được trong các hệ thống Trí tuệ nhân
tạo.

Lôgic rời rạc và tính liên tục: một thách đố lớn với các hệ thống Trí tuệ

nhân tạo là khả năng kết hợp các phương pháp xử lý thông tin trong môi trường
liên tục với các thao tác xử lý thông tin rời rạc.

Khả năng học: mặc dù hiện nay máy tính có nhiều tính năng cao nhưng

cũng không thể mô phỏng được hoàn toàn khả năng học giống bộ não con
người.

Khả năng tự tổ chức: cho tới nay, người ta chưa thể tạo lập được các hệ

thống Trí tuệ nhân tạo có khả năng tự tổ chức, tự điều khiển hoạt động của nó
để thích nghi với môi trường.

1.3.3. Những vấn đề đặt ra trong tương lai của trí tuệ nhân tạo

Trong tương lai, những nghiên cứu và ứng dụng của Trí tuệ nhân tạo tập

trung vào các vấn đề lớn sau:

Nghiên cứu và thử nghiệm các mạng Neuron, các hệ thống Trí tuệ nhân tạo

mô phỏng chức năng hoạt động của bộ não với các khả năng học, tự tổ chức, tự
thích nghi, tổng quát hoá, xử lý song song, có khả năng diễn giải, xử lý thông
tin liên tục và rời rạc.

Nghiên cứu và tạo lập các hệ thống có giao tiếp thân thiện giữa người và

máy trên cơ sở nghiên cứu nhận thức máy, thu thập và xử lý tri thức, xử lý
thông tin hình ảnh, tiếng nói.

Nghiên cứu các phương pháp biểu diễn tri thức và các phương pháp suy

diễn thông minh, các phương pháp giải quyết vấn đề đối với những bài toán phụ
thuộc không gian, thời gian.

Trí tuệ nhân tạo

Ngày nay, thế giới đang chuyển mình trong những nghiên cứu về Trí tuệ

nhân tạo. Chắc chắn rằng máy tính với trí tuệ như con người sẽ tác động mạnh
đến cuộc sống xã hội.

1.4. Các khái niệm cơ bản

Trí tuệ con người (Human Intelligence): Cho đến nay có hai khái niệm

về trí tuệ con người được chấp nhận và sử dụng nhiều nhất, đó là:

* Khái niệm trí tuệ theo quan điểm của Turing:
“Trí tuệ là những gì có thể đánh giá được thông qua các trắc nghiệm

thông minh”

* Khái niệm trí tuệ đưa ra trong tụ điển bách khoa toàn thư:
“Trí tuệ là khả năng:

Phản ứng một cách thích hợp những tình huống mới thông qua hiệu chỉnh

hành vi một cách thích đáng.

Hiểu rõ những mối liên hệ qua lại của các sự kiện của thế giới bên ngoài

nhằm đưa ra những hành động phù hợp đạt tới một mục đích nào đó.

Những nghiên cứu các chuyên gia tâm lý học nhận thức chỉ ra rằng quá

trình hoạt động trí tuệ của con người bao gồm 4 thao tác cơ bản:

- Xác định tập đích (goals).

- Thu thập các sự kiện (facts) và các luật suy diễn (inference rules) để đạt

được đích đặt ra.

- Thu gọn (pruning) quá trình suy luận nhằm xác định tập các suy diễn có

thể sử dụng được.

- Áp dụng các cơ chế suy diễn cụ thể (inference mechanisms) để đưa các

sự kiện ban đầu đi đến đích.

Trí tuệ máy: cũng không có một định nghĩa tổng quat, nhưng cũng có thể

nêu các đặc trưng chính:

- Khả năng học.

- Khả năng mô phỏng hành vi của con người.

Trí tuệ nhân tạo

- Khả năng trừu tượng hoá, tổng quát hoá và suy diễn .

- Khả năng tự giải thích hành vi.

- Khả năng thích nghi tình huống mới kể cả thu nạp tri thức và dữ liệu.

- Khả năng xử lý các biểu diễn hình thức như các ký hiệu tượng trưng.

- Khả năng sử dụng tri thức heuristic.

- Khả năng xử lý các thông tin không đầy đủ, không chính xác.

Trí tuệ nhân tạo (AI - Artificial Intelligence): có thể được định nghĩa như

một ngành của khoa học máy tính liên quan đến việc tự động hóa các hành vi
thông minh.

AI là một bộ phận của khoa học máy tính và do đó nó phải được đặt trên

những nguyên lý, lý thuyết vững chắc, có khả năng ứng dụng được. Những
nguyên lý này bao gồm: các cấu trúc dữ liệu dùng cho biểu diễn tri thức, các
thuật toán cần thiết để áp dụng những tri thức đó, cùng các ngôn ngữ và kỹ thuật
lập trình dùng cho việc cài đặt chúng.

1.5. Một số chuyên ngành (lĩnh vực ứng dụng) của trí tuệ nhân tạo

- Các phương pháp tìm kiếm lời giải

- Hệ chuyên gia

- Xử lý ngôn ngữ tự nhiên

- Lý thuyết nhận dạng

- Lập kế hoạch và Người máy (Robot)

- Máy học

- Các mô hình thần kinh (Mạng Neuron và giải thuật di truyền)

…..

Trí tuệ nhân tạo

Chương 2

BIỂU DIỄN VẤN ĐỀ TRONG KHÔNG GIAN TRẠNG THÁI

2.1. Đặt vấn đề

Trong các lĩnh vực nghiên cứu của Trí Tuệ Nhân Tạo, chúng ta thường

xuyên phải đối đầu với vấn đề (bài toán) tìm kiếm, vì thế chúng ta phải có
những kỹ thuật tìm kiếm áp dụng để giải quyết các vấn đề (bài toán) đó.

Khi giải quyết bài toán bằng phương pháp tìm kiếm, trước hết ta phải xác

định không gian tìm kiếm bao gồm tất cả các đối tượng trên đó thực hiện việc
tìm kiếm.

Nó có thể là không gian liên tục, chẳng hạn không gian các véctơ thực n

chiều, nó cũng có thể là không gian các đối tượng rời rạc.

Như vậy, ta sẽ xét việc biểu diễn một vấn đề trong không gian trạng thái

sao cho việc giải quyết vấn đề được quy về việc tìm kiếm trong không gian
trạng thái.

Một phương pháp biểu diễn vấn đề phù hợp là sử dụng các khái niệm

trạng thái (state) và toán tử (operator) [Phép biến đổi trạng thái].

Phương pháp giải quyết vấn đề dựa trên khái niệm trạng thái và toán tử

được gọi là cách tiếp cận giải quyết vấn đề nhờ không gian trạng thái.

2.2. Mô tả trạng thái

Giải bài toán trong không gian trạng thái, trước hết phải xác định dạng

mô tả trạng thái bài toán sao cho bài toán trở nên đơn giản hơn, phù hợp bản
chất vật lý của bài toán (Có thể sử dụng các xâu ký hiệu, véctơ, mảng hai chiều,
cây, danh sách).

Mỗi trạng thái chính là mỗi hình trạng của bài toán, các tình trạng ban

đầu và tình trạng cuối của bài toán gọi là trạng thái đầu và trạng thái cuối.

Ví dụ 1: Bài toán đong nước

Cho 2 bình có dung tích lần lượt là m và n (lit). Với nguồn nước không

hạn chế, dùng 2 bình trên để đong k lit nước. Không mất tính tổng quát có thể
giả thiết k <= min(m,n).

Trí tuệ nhân tạo

Tại mỗi thời điểm xác định, lượng nước hiện có trong mỗi bình phản ánh

bản chất hình trạng của bài toán ở thời điểm đó.

- Gọi x là lượng nước hiện có trong bình dung tích m và y là lượng nước

hiện có trong bình dung tích n. Như vậy bộ có thứ tự (x,y) có thể xem là trạng
thái của bài toán. Với cách mô tả như vậy, các trạng thái đặc biệt của bài toán sẽ là:

- Trạng thái đầu: (0,0)

- Trạng thái cuối: (x,k) hoặc (k,y), 0

≤

m , 0

≤

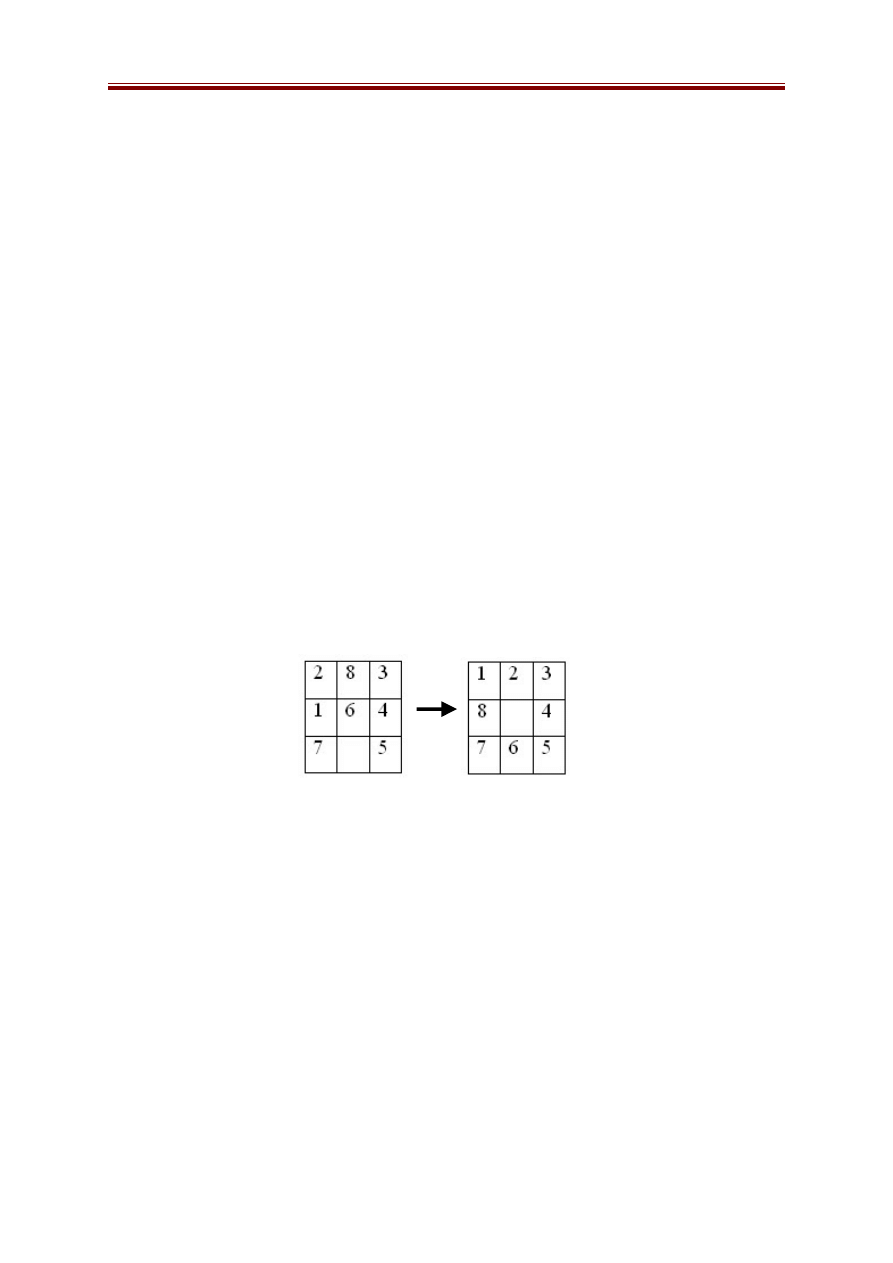
Ví dụ 2: Bài toán trò chơi 8 số

Trong bảng ô vuông 3 hàng, 3 cột , mỗi ô chứa một số nằm trong phạm vi

từ 1 đến 8 sao cho không có 2 ô có cùng giá trị, có một ô trong bảng bị trống
(không chứa giá trị nào cả. Xuất phát từ một sắp xếp nào đó các số trong bảng,
hãy dịch chuyển ô trống sang phải-right, sang trái-left, lên trên-up hoặc xuống
dưới-down (nếu có thể được) để đưa bảng ban đầu về bảng qui ước trước.

Chẳng hạn Hình 2.1 trên đây là bảng xuất phát và Hình 2.2 là bảng mà ta

phải thực hiện các bước di chuyển ô trống để đạt được.

Hình 2.1 Hình 2.2

Giá trị các phần tử trong bảng xác định trạng thái bài toán. Vì vậy có thể

mô tả trạng thái của bài toán bằng một ma trận A

3*3

= (a

), a

∈

{0..8}, a

< > a

∀

i<>k, j<> l.

- Trạng thái đầu của bài toán là ma trận:

- Trạng thái cuối là ma trận:













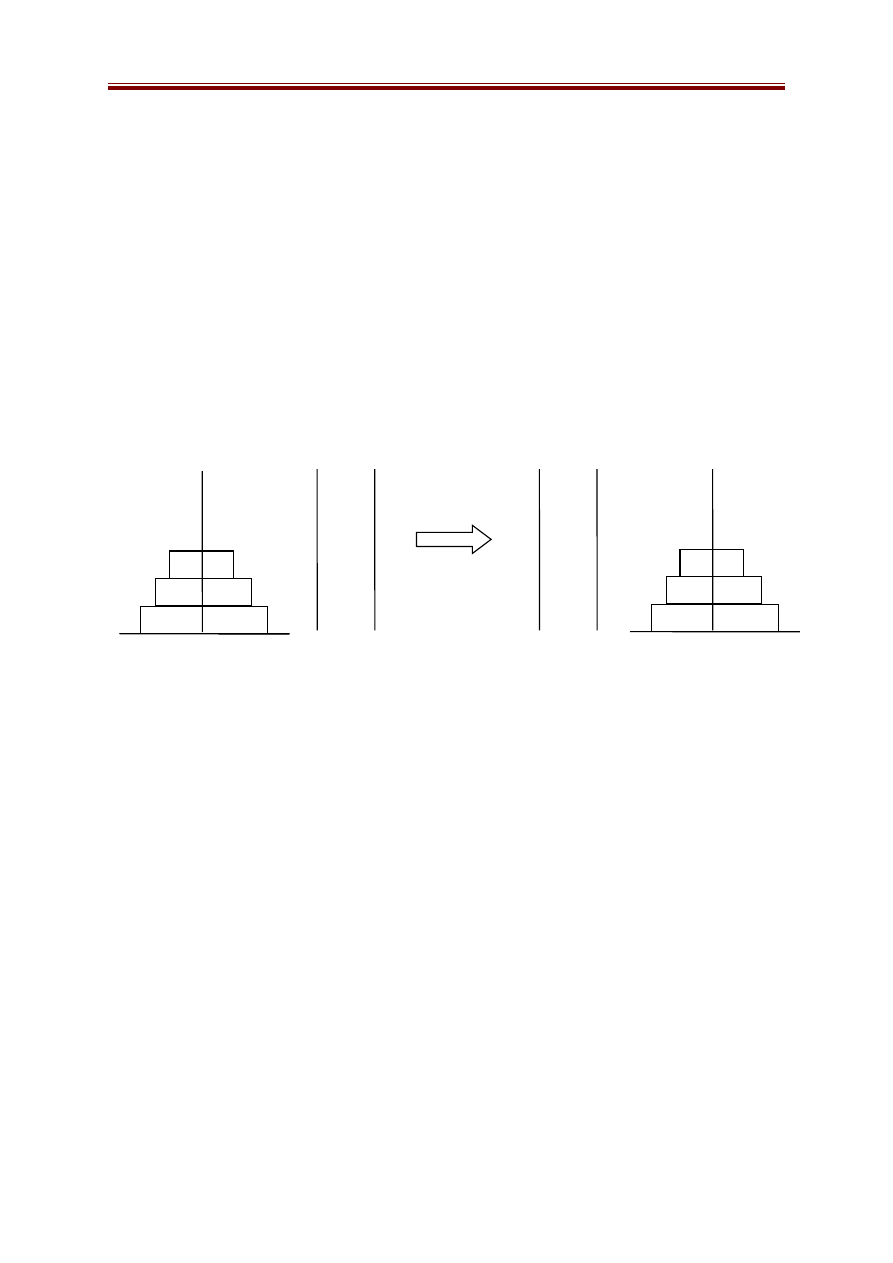
Trí tuệ nhân tạo

Có thể phát biểu dạng tổng quát của bài toán này (Trò chơi n

-1 số).

Ví dụ 3: Bài toán tháp Hà Nội

Cho ba cọc 1, 2, 3. Ở cọc 1 ban đầu có n đĩa sắp xếp theo thứ tự to dần từ

dưới lên trên. Hãy dịch chuyển n đĩa đó sang cọc thứ 3 sao cho:

- Mỗi lần chỉ chuyển một đĩa.

- Trong mỗi cọc không cho phép đĩa to nằm trên đĩa nhỏ hơn.

Hình 2.3. Bài toán tháp Hà Nội (n=3)

Bài toán xác định khi biết được từng đĩa đang nằm ở cọc nào. Hay nói

cách khác, có hai cách xác định:

- Cọc 1 hiện đang chứa những đĩa nào? Cọc 2 hiện đang chứa những đĩa

nào? Và cọc 3 đang chứa những đĩa nào.

- Đĩa lớn thứ i hiện đang nàm ở cọc nào? ( i = 1 … n )

Như vậy cách mô tả trạng thái bài toán không duy nhất, vấn đề là chọn

cách mô tả nào để đạt được mục đích dễ dàng nhất.

Theo trên, với cách thứ nhất ta phải dùng 3 danh sách động vì số đĩa trên

mỗi cọc là khác nhau trong từng thời điểm khác nhau.













Trí tuệ nhân tạo

Cách thứ hai, nhìn qua thì khó mô tả nhưng dựa vào khái niệm về bộ có

thứ tự trong toán học, cách này mô tả bài toán hiệu quả hơn. Thật vậy, nếu gọi
x

là cọc chứa đĩa lớn thứ i, trong đó x

∈

{1, 2, 3}, i

∈

{1 ..n}. Khi đó bộ có thứ tự

, x

, . . ,x

) có thể dùng làm dạng mô tả trạng thái đang xét của bài toán. Với

cách mô tả này thì:

- Trạng thái đầu là (1,1,. . .,1)
- Trạng thái cuối là (3,3,. . .,3)

2.3. Toán tử chuyển trạng thái

Toán tử chuyển trạng thái thực chất là các phép biến đổi đưa từ trạng thái

này sang trạng thái khác. Có hai cách dùng để biểu diễn các toán tử:

- Biểu diễn như một hàm xác định trên tập các trạng thái và nhận giá trị

cũng trong tập này.

- Biểu diễn dưới dạng các quy tắc sản xuất S? A có nghĩa là nếu có trạng

thái S thì có thể đưa đến trạng thái A.

Ví dụ 1: Bài toán đong nước

Các thao tác sử dụng để chuyển trạng thái này sang trạng thái khác gồm:
Đổ đầy một bình, đổ hết nước trong một bình ra ngoài, đổ nước từ bình

này sang bình khác. Như vậy, nếu trạng thái đang xét là (x,y) thì các trạng thái
kế tiếp có thể chuyển đến sẽ là:

(m,y)

(x,n)

(0,y)

(x,0)

(x,y)

(0, x+ y) nếu x+y < = n

(x+y -n,n) nếu x+y > n

(x+ y,0) nếu x+y < = m

(m, x+y-m) nếu x+y > m

Trí tuệ nhân tạo

Ví dụ 2: Trò chơi 8 số

Các thao tác để chuyển trạng thái tương ứng với việc chuyển ô trống sang

phải, sang trái, lên, xuống nếu có thể được.

- Biểu diễn theo quy tắc sản xuất:

- Biểu diễn theo một hàm:

Gọi hàm f

là hàm biểu diễn cho toán tử chuyển ô trống lên trên; gọi B

(B= (b

)) là trạng thái sau khi di chuyển ô trống ở trạng thái A (A= (a

)) lên

trên, nghĩa là: B= f

(A), giả sử ô trống đang ở vị trí (i

, j

) (hay nói cách khác a

= 0) thì hàm f được xác định như sau:

∀

(i, j)

nếu i

= 1

) =

nếu (i, j)

≠

-1, j

) và (i, j)

≠

, j

) và i

i0-1, j0

nếu (i, j) = (i

, j

), i

i0, j0

nếu (i, j) = (i

-1, j

), i

Tương tự, có thể xác định các phép chuyển ô trống xuống dưới f

, qua trái

, qua phải f

như sau:

∀

(i, j)

nếu i

= 3

) =

nếu (i, j)

≠

+1, j

) và (i, j)

≠

, j

) và i

i0-1, j0

nếu (i, j) = (i

, j

), i

i0, j0

nếu (i, j) = (i

+1, j

), i

∀

(i, j)

nếu j

= 1

Trí tuệ nhân tạo

) =

nếu (i, j)

≠

, j

-1) và (i, j)

≠

, j

) và j

> 1

i0-1, j0

nếu (i, j) = (i

, j

), j

> 1

i0, j0

nếu (i, j) = (i

, j

-1), j

> 1

∀

(i, j)

nếu j

= 3

) =

nếu (i, j)

≠

, j

+1) và (i, j)

≠

, j

) và j

< 3

i0-1, j0

nếu (i, j) = (i

, j

), j

< 3

i0, j0

nếu (i, j) = (i

, j

+1), j

< 3

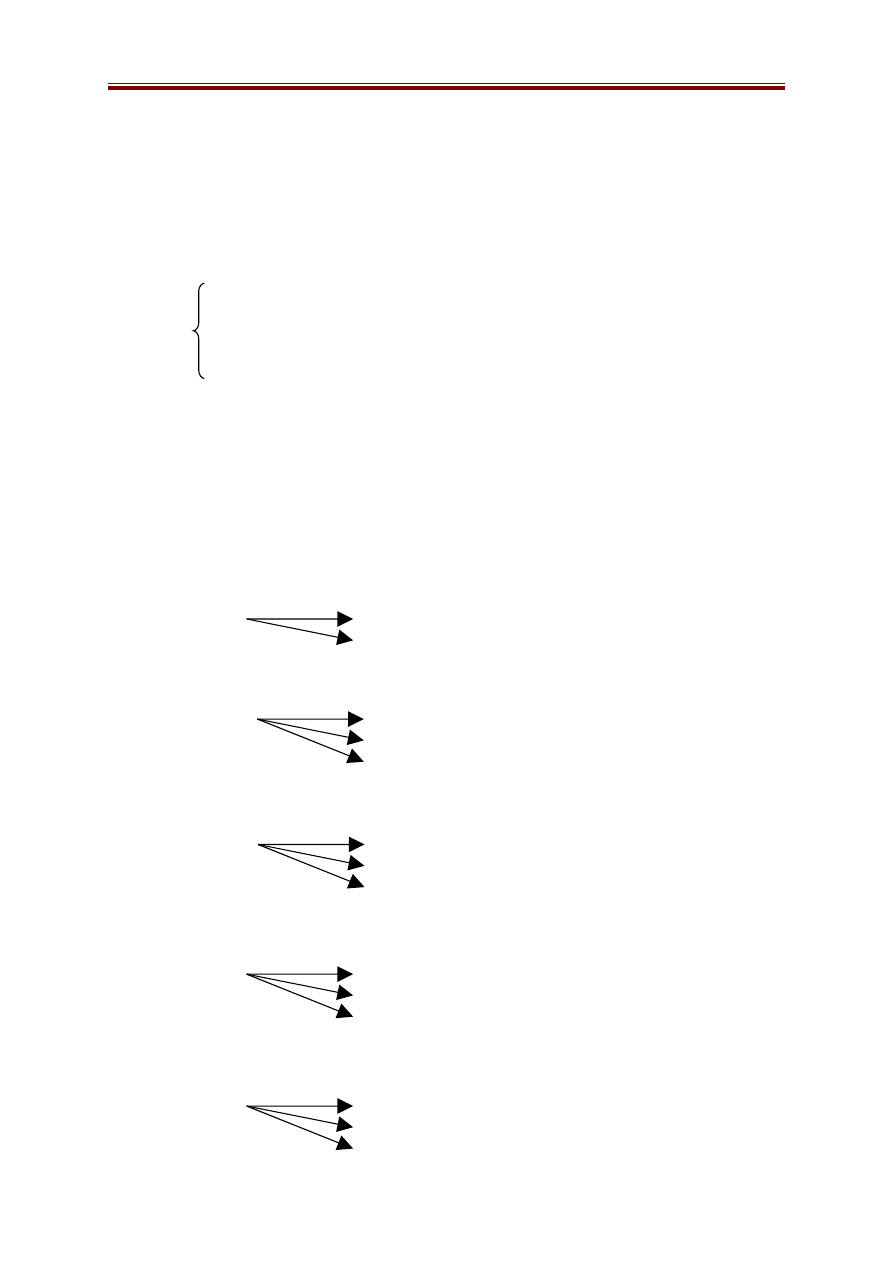
Ví dụ 3: Bài toán Tháp Hà Nội với n=3.

Mỗi trạng thái là một bộ ba (i, j, k). Có các trường hợp như sau:

- Ba đĩa cùng nằm trên một cọc: (i, i, i)

- Hai đĩa cùng nằm trên một cọc: (i, i, j), (i, j, i), (j, i, i)

- Ba đĩa nằm trên ba cọc phân biệt: (i, j, k)

(i, i, i)

(i, i, j)

(i, i, k)

(i, i, j)

(i, i, k)

(i, k, j)

(i, i, i)

(i, j, i)

(i, j, k)

(i, j, j)

(i, k, i)

(j, i, i)

(j, i, j)

(j, i, k)

(k, i, i)

(i, j, k)

(i, i, k)

(i, j, j)

Trí tuệ nhân tạo

(i, j, i)

2.4. Không gian trạng thái của bài toán

Không gian trạng thái là tập tất cả các trạng thái có thể có và tập các toán

tử của bài toán.

Không gian trạng thái là một bộ bốn, Ký hiệu: K= (T, S, G, F). Trong đó:

T: tập tất cả các trạng thái có thể có của bài toán

S: trạng thái đầu

G: tập các trạng thái đích

F: tập các toán tử

Ví dụ 1: Không gian trạng thái của bài toán đong nước là bộ bốn T, S, G,

F xác đinh như sau:

4 T = { (x,y) / 0 <= x <= m; 0 <= y <= n }
5 S = (0,0)
6 G = { (x,k) hoặc (k,y) / 0 <= x <= m; 0 <= y <= n}
7 F = Tập các thao tác đong đầy, đổ ra hoặc đổ sang bình khác thực hiện trên

một bình.

Ví dụ 2: Không gian trạng thái của bài toán Tháp Hà nội với n = 3:

T = { (x1, x2, x3)/ xi

∈

{1, 2, 3} }

S = (1, 1, 1)

G = {(3, 3, 3)}

F = Tập các khả năng có thể chuyển đĩa đã xác định trong phần

trước.

Ví dụ 3: Không gian trạng thái của bài toán trò chơi 8 số:

T = { (a

)

3x3

/ 0<= a

<= 8 và a

<> a

với i<> j hoặc k <> l}

S = Ma trận xuất phát của bài toán

Trí tuệ nhân tạo

G = Ma trận cuối cùng của bài toán (các số nằm theo vị trí yêu

cầu)

F = {f

, f

}

Tìm kiếm lời giải trong không gian trạng thái là quá trình tìm kiếm xuất

phát từ trạng thái ban đầu, dựa vào toán tử chuyển trạng thái để xác định các
trạng thái tiếp theo cho đến khi gặp được trạng thái đích.

Như vậy, muốn biểu diễn một vấn đề trong không gian trạng thái, ta cần

xác định các yếu tố sau:

- Trạng thái ban đầu.

- Một tập hợp các toán tử. Trong đó mỗi toán tử mô tả một hành động

hoặc một phép biến đổi có thể đưa một trạng thái tới một trạng thái khác.

Tập hợp tất cả các trạng thái có thể đạt tới từ trạng thái ban đầu bằng cách

áp dụng một dãy toán tử, lập thành không gian trạng thái của vấn đề.

2.5. Biểu diễn không gian trạng thái dưới dạng đồ thị

2.5.1. Các khái niệm

•

Đồ thị G = (V,E) trong đó V:tập đỉnh, E: tập cung (E

⊂

V*V)

Chú ý:
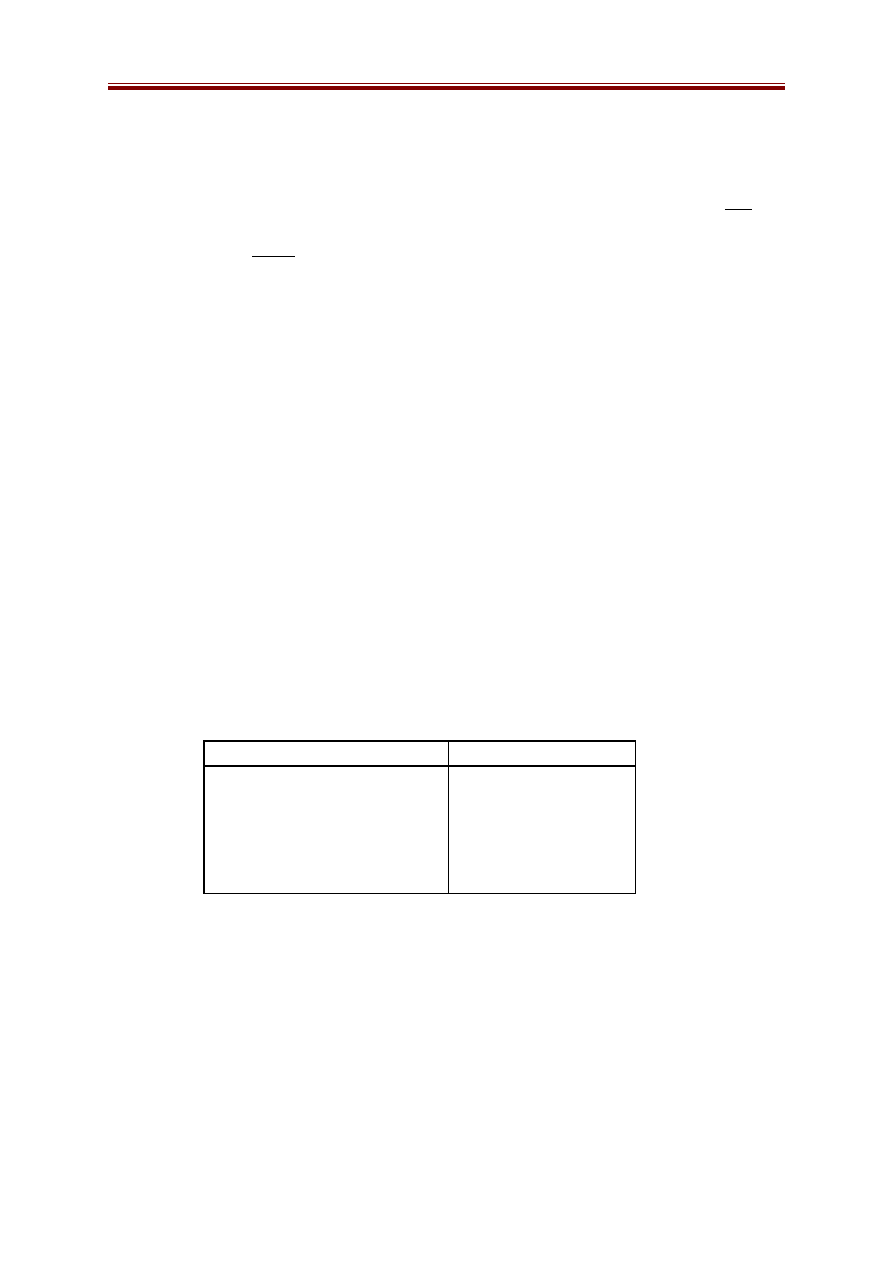
- G là đồ thị vô hướng thì (i, j) là một cạnh cũng như là (j, i) (tức là:(i,

∈

E thì (j,i)

∈

E).

- Nếu G là đồ thị có hướng thì cung (i, j) hoàn toàn khác với cung (j, i).

Ví dụ: Xét đồ thị vô hướng G

và đồ thị có hướng G

•

Tập đỉnh kề:

Trí tuệ nhân tạo

∀

∈

V, T(n)={m

∈

V/ (n,m)

∈

E} được gọi là tập các đỉnh kề của n.

•

Đường đi:

p = (n

,...,n

) được gọi là đường đi từ đỉnh n

→

nếu n

∈

∀

i=1,k

, n

i+1

)

∈

∀

i=1, k -1.

•

Cây là đồ thị có đỉnh gốc n

∈

V thoả:

Một đồ thị G=(V, E) gọi là cây nếu tồn tại một đỉnh n

∈

V có những tính

chất sau:

∧

∀

∈

V, n

∈

T(n

), trong đó T(n

): tập các đỉnh thuộc dòng dõi của n

là tổ tiên của n).

∀

∈

∃!

∈

V sao cho n

∈

T(m), m được gọi là cha của n.

2.5.2. Biểu diễn không gian trạng thái bằng đồ thị

Theo ngôn ngữ đồ thị, không gian trạng thái tương ứng với một đồ thị

định hướng trong đó: Các trạng thái tương ứng với các đỉnh trong đồ thị, nếu
tồn tại toán tử chuyển trạng thái thì có cung (s, t).

Để thấy rõ mối tương quan, ta có bảng sau:

KGTT

Đồ thị

Trạng thái

Toán tử

Dãy các trạng thái liên tiếp

Đỉnh

Cung

Đường đi

2.5.3. Biểu diễn đồ thị

Cho đồ thị G = (V,E), giả sử V={1, 2,....,n}. Có hai cách thường dùng để

biểu diễn đồ thị G lưu trữ trong máy tính.

* Biểu diễn bằng ma trận kề

Đồ thị G được biểu diễn bởi ma trận kề A=(a

)

nxn

với n là số đỉnh của đồ

thị, trong đó:

Trí tuệ nhân tạo

nếu (i, j)

∈

trong trường hợp ngược lại

Nếu G là đồ thị vô hướng thì ma trận kề A là ma trận đối xứng.

Ví dụ: Với đồ thị vô hướng G

và đồ thị có hướng G

ở trên ta có các ma

trận kề sau:

* Biểu diễn bằng danh sách kề

Với mỗi đỉnh i của đồ thị, ta có một danh sách tất cả các đỉnh kề với i, ta

ký hiệu là List(i). Để thể hiện List(i) ta có thể dùng mảng, kiểu tập hợp hay kiểu
con trỏ. Ví dụ với đồ thị G1, ta có List(1)= [2, 3, 4]

Trí tuệ nhân tạo

Ví dụ 1: Bài toán đong nước m=3, n=2, k=1

(0,0)

(3,0)

(0,2)

(1,2)

(3,2)

(2,0)

(1,0)

(0,1) (2,2)

(3,1)

Ví dụ 2: Tháp Hà Nội với n = 3

111

(111)

(112)

(113)

(132)

(123)

(133)

(131)

(121) (122)

(233)

(322)

(231) (232)

(323)

(321)

(221) (212)

(313)

(331)

(222) (223) (213)

(211)

(311)

(312) (332)

(333)

Trí tuệ nhân tạo

Chương 3

CÁC PHƯƠNG PHÁP TÌM KIẾM LỜI GIẢI TRONG

KHÔNG GIAN TRẠNG THÁI

3.1. Đặt vấn đề

Quá trình tìm kiếm lời giải của bài toán được biểu diễn trong không gian

trạng thái được xem như quá trình dò tìm trên đồ thị, xuất phát từ trạng thái ban
đầu, thông qua các toán tử chuyển trạng thái, lần lượt đến các trạng thái tiếp
theo cho đến khi gặp được trạng thái đích hoặc không còn trạng thái nào có thể
tiếp tục được nữa.

Khi áp dụng các phương pháp tìm kiếm trong không gian trạng thái,

người ta thường quan tâm đến các vấn đề sau:

- Kỹ thuật tìm kiếm lời giải

- Phương pháp luận của việc tìm kiếm

- Chiến lược tìm kiếm

Tuy nhiên, không phải các phương pháp này có thể áp dụng để giải quyết

cho tất cả các bài toán phức tạp mà chỉ cho từng lớp bài toán.

Việc chọn chiến lược tìm kiếm cho bài toán cụ thể phụ thuộc nhiều vào

các đặc trưng của bài toán.

* Chúng ta lần lượt nghiên cứu các kỹ thuật sau:

- Các kỹ thuật tìm kiếm mù: trong đó chúng ta không có hiểu biết gì về

các đối tượng để hướng dẫn tìm kiếm mà chỉ đơn thuần là xem xét theo một hệ
thống nào đó tất cả các đối tượng để phát hiện ra đối tượng cần tìm.

- Các kỹ thuật tìm kiếm kinh nghiệm (tìm kiếm heuristic): trong đó chúng

ta dựa vào kinh nghiệm và sự hiểu biết của chúng ta về vấn đề cần giải quyết để
xây dựng nên hàm đánh giá hướng dẫn sự tìm kiếm.

- v.v…

* Các chiến lược tìm kiếm có thể phân thành hai loại:

Trí tuệ nhân tạo

- Các chiến lược tìm kiếm mù: Trong các chiến lược tìm kiếm này, không

có một sự hướng dẫn nào cho sự tìm kiếm, mà ta chỉ phát triển các trạng thái
ban đầu cho tới khi gặp một trạng thái đích nào đó. Có hai kỹ thuật tìm kiếm mù
cơ bản, đó là tìm kiếm theo bề rộng (chiều rộng) và tìm kiếm theo độ sâu (chiều
sâu).

- Tìm kiếm kinh nghiệm (tìm kiếm heuristic): Trong rất nhiều vấn đề,

chúng ta có thể dựa vào sự hiểu biết của chúng ta về vấn đề, dựa vào kinh
nghiệm, trực giác, để đánh giá các trạng thái.

Ở tìm kiếm kinh nghiệm sử dụng sự đánh giá các trạng thái để hướng dẫn

sự tìm kiếm: trong quá trình phát triển các trạng thái, ta sẽ chọn trong số các
trạng thái chờ phát triển, trạng thái được đánh giá là tốt nhất để phát triển. Do
đó tốc độ tìm kiếm sẽ nhanh hơn.

Các phương pháp tìm kiếm dựa vào sự đánh giá các trạng thái để hướng

dẫn sự tìm kiếm gọi chung là các phương pháp tìm kiếm kinh nghiệm.

Như vậy, chiến lược tìm kiếm được xác định bởi chiến lược chọn trạng

thái để phát triển ở mỗi bước:

Trong tìm kiếm mù: ta chọn trạng thái để phát triển theo thứ tự mà chúng

được sinh ra.

Trong tìm kiếm kinh nghiệm: ta chọn trạng thái dựa vào sự đánh giá các

trạng thái.

* Các thủ tục tìm kiếm điển hình bao gồm:

- Tìm kiếm theo chiều rộng (Breadth – First Search)

- Tìm kiếm theo chiều sâu (Depth – First Search)

- Tìm kiếm sâu dần (Depthwise Search)

- Tìm kiếm cực tiểu hoá giá thành (Cost minimization Search).

- Tìm kiếm với tri thức bổ sung (Heuristic Search).

A - TÌM KIẾM MÙ

Trí tuệ nhân tạo

3.2. Phương pháp tìm kiếm theo chiều rộng

3.2.1. Kỹ thuật tìm kiếm rộng

Kỹ thuật tìm kiếm rông là tìm kiếm trên tất cả các nút của một mức trong

không gian bài toán trước khi chuyển sang các nút của mức tiếp theo.

Kỹ thuật tìm kiếm rộng bắt đầu từ mức thứ nhất của không gian bài toán,

theo hướng dẫn của luật trọng tài, chẳng hạn “đi từ trái sang phải”. Nếu không
thấy lời giải tại mức này, nó chuyển xuống mức sau để tiếp tục … đến khi định
vị được lời giải nếu có.

3.2.2. Giải thuật

Input:

Cây/Đồ thị G = (V,E) với đỉnh gốc là n

(trạng thái đầu)

Tập đích Goals

Output:

Một đường đi p từ n

đến một đỉnh n

∈

Goals

Method:

Sử dụng hai danh sách hoạt động theo nguyên tắc FIFO (queue) MO và

DONG

Procedure BrFS; (Breadth First Search)

Begin

Append(MO,n

)

DONG=null;

While MO <> null do

begin

n:= Take(MO);

if n

∈

DICH then exit;

Append(DONG, n);

Trí tuệ nhân tạo

For m

∈

T(n) and m

∉

DONG+MO do

Append(MO, m);

end;

Write (‘Không có lời giải’);

End;

Chú ý: Thủ tục Append(MO,n

) bổ sung một phần tử vào queue MO.

Hàm Take(MO) lấy một phần tử trong queue MO.

3.2.3. Đánh giá độ phức tạp của giải thuật tìm kiếm rộng

Giả sử rằng, mỗi trạng thái khi được xét sẽ sinh ra k trạng thái kế tiếp.

Khi đó ta gọi k là nhân tố nhánh. Nếu bài toán tìm được nghiệm theo phương
pháp tìm kiếm rộng có độ dài d. Như vậy, đỉnh đích sẽ nằm ở mức d, do đó số
đỉnh cần xét lớn nhất là:

1 + k + k

+ . . . + k

Như vậy độ phức tạp thời gian của giải thuật là O(k

). Độ phức tạp không

gian cũng là O(k

), vì tất cả các đỉnh của cây tìm kiếm ở mức d đều phải lưu vào

danh sách.

3.2.4. Ưu và nhược điểm của phương pháp tìm kiếm rộng

* Ưu điểm:

•

Kỹ thuật tìm kiếm rộng là kỹ thuật vét cạn không gian trạng thái

bài toán vì vậy sẽ tìm được lời giải nếu có.

•

Đường đi tìm được đi qua ít đỉnh nhất.

•

Thuận lợi khi muốn tìm nhiều lời giải.

* Nhược điểm:

•

Tìm kiếm lời giải theo thuật toán đã định trước, do vậy tìm kiếm

một cách máy móc; khi không có thông tin hổ trợ cho quá trình tìm kiếm,
không nhận ra ngay lời giải.

•

Không phù hợp với không gian bài oán kích thước lớn. Đối với loại

bài toán này, phương pháp tìm rộng đối mặt với các nhu cầu:
-

Cần nhiều bộ nhớ theo số nút cần lưu trữ.

(0;0)

(0;4)

(4;0)

(4;4)

Trí tuệ nhân tạo

Cần nhiều công sức xử lý các nút, nhất là khi các nhánh cây dài, số nút
tăng.

Dễ thực hiện các thao tác không thích hợp, thừa, đưa đến việc tăng
đáng kể số nút phải xử lý.

•

Không hiệu qủa nếu lời giải ở sâu. Phương pháp này không phù hợp cho

trường hợp có nhiều đường dẫn đến kết quả nhưng đều sâu.

•

Giao tiếp với người dùng không thân thiện. Do duyệt qua tất cả các nút,

việc tìm kiếm không tập trung vào một chủ đề.

3.2.5. Các ví dụ

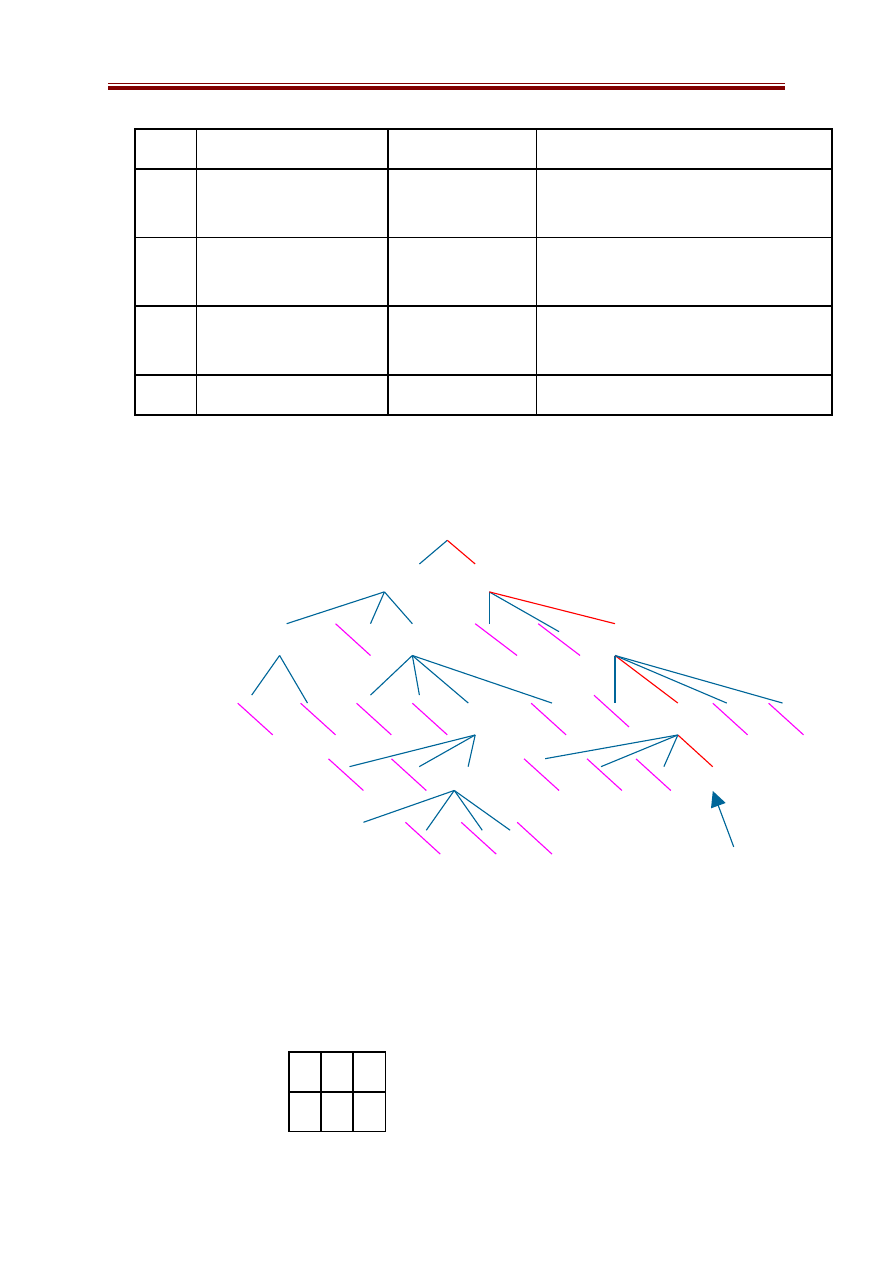
Ví dụ 1: Bài toán đong nước với m = 5, n= 4, k =3.

Mức 1: Trạng thái đầu (0;0)

Mức 2: Các trạng thái (5;0), (0;4) Mức 3: (5;4), (1;4), (4,0)

Mức 4: (1;0), (4;4)

Mức 5: (0;1), (5;3)

Ở mức 5 ta gặp trạng thái đích là (5;3) vì vậy có được lời giải như sau:

(0;0)

→

(0;4)

→

(4;0)

→

(4;4)

→

(5;3)

Để có được lời giải này ta phải lưu lại vết của đường đi, có thể trình bày

quá trình tìm kiếm dưới dạng bảng sau:

T(i)

↑

↓

DONG

(0;0)

(0;0) (5;0) (0;4)

(5;0) (0;4)

(0;0)

(5;0) (5;4) (0;0) (1;4)

(0;4) (5;4)
(1;4)

(0;0) (5;0)

(0;4) (5;4) (0;0) (4;0)

(5;4) (1;4)
(4;0)

(0;0) (5;0) (0;4)

(5;4) (0;4) (5;0)

(1;4) (4;0)

(0;0) (5;0) (0;4) (5;4)

(1;4) (5;4) (0;4) (1;0)

(5;0)

(4;0) (1;0)

(0;0) (5;0) (0;4) (5;4) (1;4)

(4;0) (5;0) (4;4) (0;0) (1;0) (4;4)

(0;0) (5;0) (0;4) (5;4) (1;4) (4;0)

(0;0)

(0;4)

(4;0)

(4;4)

Trí tuệ nhân tạo

(0;4)

(1;0) (5;0) (1;4) (0;1)

(4;4) (0;1)

(0;0) (5;0) (0;4) (5;4) (1;4) (4;0)
(1;0)

(4;4) (5;4) (0;4) (4;0)

(5;3)

(0;1) (5;3)

(0;0) (5;0) (0;4) (5;4) (1;4) (4;0)
(1;0) (4;4)

(0;1) (5;1) (0;4) (0;0)

(1;0)

(5;3) (5;1)

(0;0) (5;0) (0;4) (5;4) (1;4) (4;0)
(1;0) (0;1)

(5;3)

Ta có thể biểu diễn dưới dạng đồ thị sau:

Ví dụ 2: Bài toán trò chơi 8 số.

Bảng xuất phát

2 8 3

1 6 4

(0;0)

(5;0)

(0;4)

(1;4)

(5;4) (0;0)

(4;0)

(5;4) (0;0)

(5;0)

(0;4)

(5;4)

(1;0) (5;0)

(4;4)

(5;0)

(0;0)

(0;4)

(1;4)

(5;0)

(0;1)

(0;4)

(5;4)

(4;0)

(5;3)

(0;4)

(5;1)

(0;0) (1;0)

Mức 1

Mức 2

Mức 3

Mức 4

Mức 5

Đích

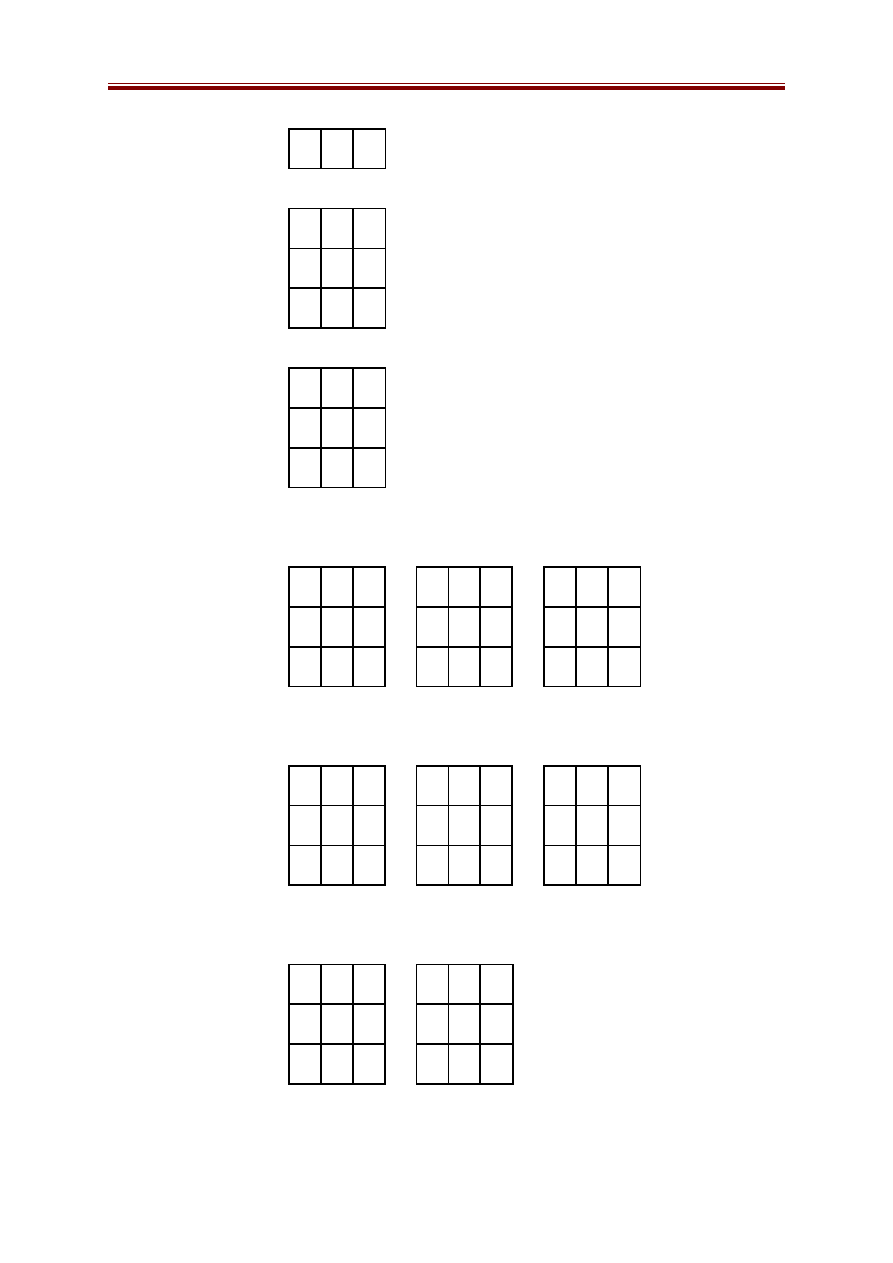
Trí tuệ nhân tạo

Bảng kết thúc

1 2 3

7 6 5

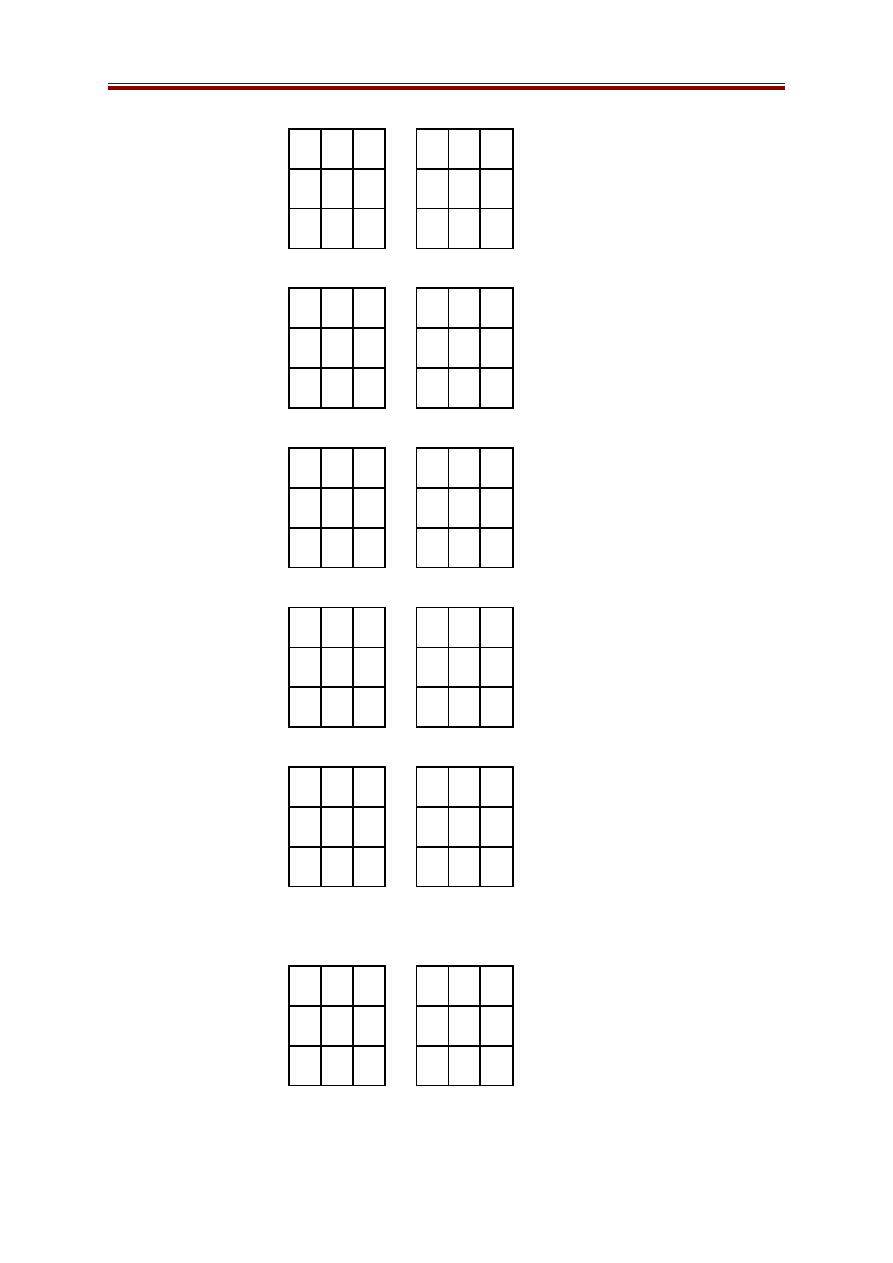
Mức 1: Có một trạng thái

2 8 3

1 6 4

Mức 2: Có ba trạng thái

2 8 3

1 6 4

7 6 5

7 5

Mức 3: Có năm trạng thái

2 8 3

1 4

1 8 4

7 6 5

2 8 3

6 4

1 6

1 7 5

7 5 4

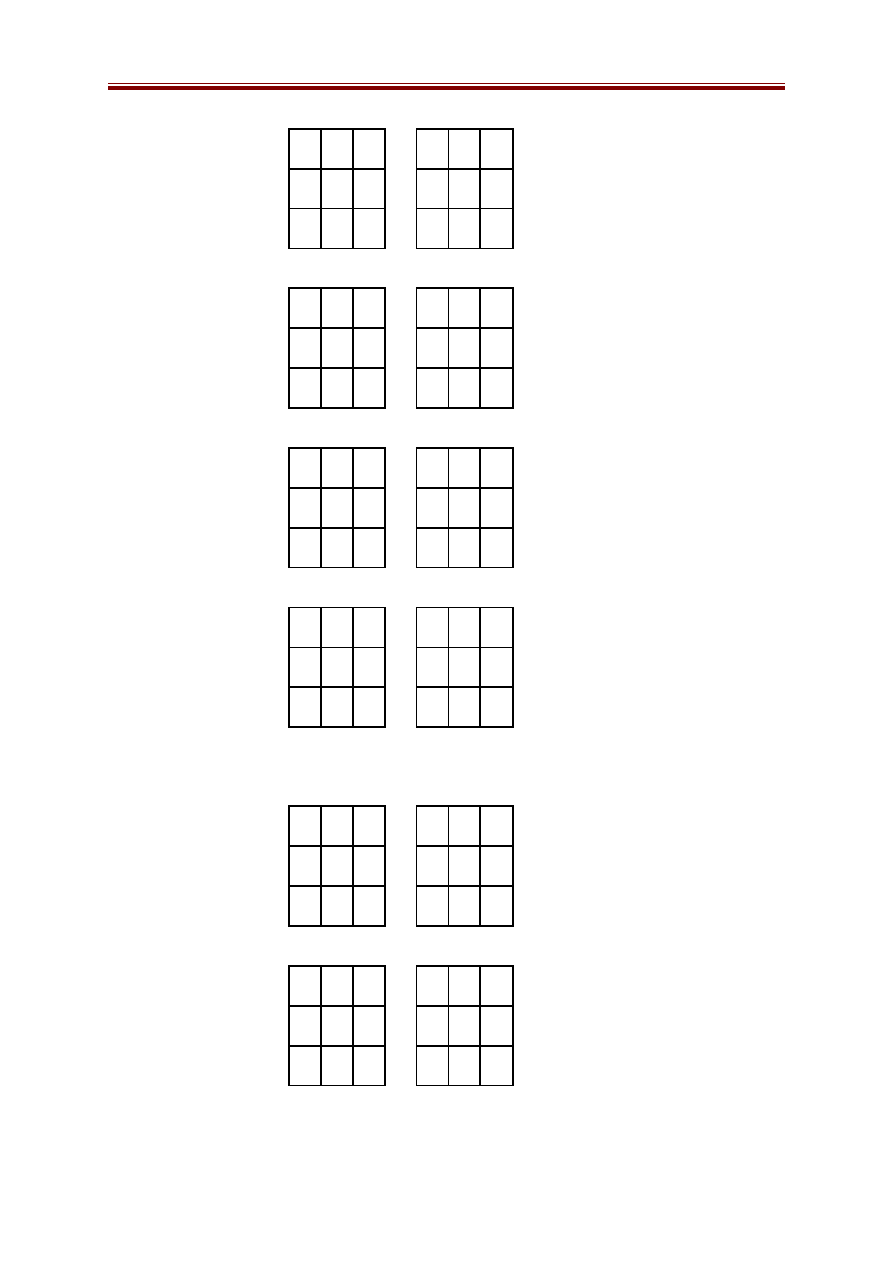
Mức 4: Có mười trạng thái

Trí tuệ nhân tạo

8 3

2 8 3

2 1 4

7 1 4

7 6 5

6 5

2 8

2 8 3

1 4 3

1 4 5

1 7 5

7 6

2 3

1 8 4

7 6 5

8 3

2 8 3

2 6 4

1 7 5

2 8

2 8 3

1 6 3

1 6 4

7 5 4

7 5

Mức 5: Có 12 trạng thái

1 2 3

2 3 4

8 4

1 8

7 6 5

Trí tuệ nhân tạo

2 8 3

2 1 4

7 1 4

7 6 5

2 8 3

1 4 3

1 4 5

7 6 5

2 6 4

6 8 4

1 7 5

2 8 3

6 7 4

1 6 3

7 5 4

2 8 3

1 8 3

1 5 6

7 5 4

Mức 6: Có 24 trạng thái

1 2 3

7 8 4

7 6 5

6 5

. . .

Ở mức này ta gặp được trạng thái đích

Trí tuệ nhân tạo

1 2 3

7 6 5

3.3. Phương pháp tìm kiếm theo chiều sâu

3.3.1. Kỹ thuật tìm kiếm sâu

Tìm kiếm sâu trong không gian bài toán được bắt đầu từ một nút rồi tiếp

tục cho đến khi hoặc đến ngõ cụt hoặc đến đích. Tại mỗi nút có luật trong tài,
chẳng hạn, “đi theo nút cực trái”, hướng dẫn việc tìm. Nếu không đi tiếp được,
gọi là đến ngõ cụt, hệ thống quay lại một mức trên đồ thị và tìm theo hướng
khác, chẳng hạn, đến nút “sát nút cực trái”. Hành động này gọi là quay lui.

Thuật toán tìm kiếm theo chiều sâu được hình dung như việc khảo sát

một cây bắt đầu từ gốc đi theo mọi cành có thể được, khi gặp cành cụt thì quay
lại xét cành chưa đi qua.

- Ở bước tổng quát, giả sử đang xét đỉnh i, khi đó các đỉnh kề với i có các

trường hợp:

+ Nếu tồn tại đỉnh j kề i chưa được xét thì xét đỉnh này (nó trở

thành đỉnh đã xét) và bắt đầu từ đó tiếp tục quá trình tìm kiếm với đỉnh
này..

+ Nếu với mọi đỉnh kề với i đều đã được xét thì i coi như duyệt

xong và quay trở lại tìm kiếm từ đỉnh mà từ đó ta đi đến được i.

3.3.2. Giải thuật

Input:

Cây/Đồ thị G = (V,E) với đỉnh gốc là n

(trạng thái đầu)

Tập đích Goals

Output:

Một đường đi p từ n

đến một đỉnh n

∈

Goals

Method:

Trí tuệ nhân tạo

Sử dụng hai danh sách hoạt động theo nguyên tắc LIFO (Stack) MO và

DONG

Procedure DFS; (Depth First Search)

Begin

Push (MO,n

)

DONG=null;

While MO <> null do

begin

n:=pop (MO);

if n

∈

DICH then exit;

push (DONG, n);

For m

∈

T(n) and m

∉

DONG+MO do

Push (MO, m);

end;

Write (‘Không có lời giải’);

End;

Chú ý: Thủ tục Push(MO,n

) thực hiện việc bổ sung n

vào stack MO

Hàm Pop(MO) lấy phần tử đầu tiên trong Stack MO.

3.3.3. Đánh giá độ phức tạp của thuật toán tìm kiếm sâu

Giả sử nghiệm của bài toán là đường đi có độ dài d, cây tìm kiếm có nhân

tố nhánh là k. Có thể xảy ra nghiệm là đỉnh cuối cùng được xét ở mức d+1 theo
luật trọng tài. Khi đó độ phức tạp thời gian của thuật toán tìm kiếm theo chiều
sâu trong trường hợp xấu nhất là O(k

Để đánh giá độ phức tạp không gian của thuật toán tìm kiếm sâu ta có

nhận xét ràng: Khi xét đỉnh j, ta chỉ cần lưu các đỉnh chưa được xét mà chúng là

Trí tuệ nhân tạo

những đỉnh con của những đỉnh nằm trên đường đi từ đỉnh gốc đến j. Vì vậy chỉ
cần lưu tối đa la k*d. Do đó độ phức tạp không gian của thuật toán là O(k*d).

3.3.4. Ưu và nhược điểm của phương pháp tìm kiếm sâu

* Ưu điểm:

•

Nếu bài toán có lời giải, phương pháp tìm kiếm sâu bảo đảm tìm ra lời giải.

•

Kỹ thuật tìm kiếm sâu tập trung vào đích, con người cảm thấy hài lòng khi
các câu hỏi tập trung vào vấn đề chính.

•

Do cách tìm của kỹ thuật này, nếu lời giải ở rất sâu, kỹ thuật tìm sâu sẽ tiết
kiệm thời gian.

•

Thuận lợi khi muốn tìm một lời giải

* Nhược điểm:

•

Tìm sâu khai thác không gian bài toán để tìm lời giải theo thuật toán đơn

giản một cách cứng nhắc. Trong quá trình tìm nó không có thông tin nào hổ
trợ để phát hiện lời giải. Nếu chọn nút ban đầu không thích hợp có thể
không dẫn đến đích của bài toán.

•

Không phù hợp với không gian bài toán lớn, kỹ thuật tìm kiếm sâu có thể

không đến lời giải trong khoảng thời gian vừa phải.

3.3.5. Các ví dụ

Ví dụ 1: Bài toán đong nước với m = 5, n = 4, k = 3.

Chú ý: Nếu ta chọn nhánh ưu tiên đổ đầy bình thứ hai thì sẽ tìm thấy lời

giải rất nhanh. Quá trình tìm kiếm có thể trình bày bằng bảng sau.

T(i)

↓↑

DONG

(0;0)

(0;0) (5;0) (0;4)

(5;0) (0;4)

(0;0)

(0;4) (5;4) (0;0) (4;0)

(5;0) (5;4)
(4;0)

(0;0) (0;4)

(4;0) (5;0) (4;4) (0;0) (5;0) (5;4) (0;0) (0;4) (4;0)

Trí tuệ nhân tạo

(0;4)

(4;4)

(4;4) (5;4) (0;4) (4;0)

(5;3)

(5;0) (5;4)
(5;3)

(0;0) (0;4) (4;0) (4;4)

(5;3)

Lời giải tìm được: (0;0)

→

(0;4)

→

(4;0)

→

(4;4)

→

(5;3)

Ví dụ 2: Bài toán Tháp Hà nội với n = 3.
Nhắc lại, dùng bộ ba (x

; x

) biểu diễn trạng thái bài toán, với x

là cọc

chứa đĩa lớn thứ i.

T(i)

↓↑

DONG

(1;1;1)

(1;1;1) (1;1;2) (1;1;3)

(1;1;2) (1;1;3)

(1;1;1)

(1;1;3) (1;1;1)(1;1;2)

(1;2;3)

(1;1;2)(1;2;3)

(1;1;1)(1;1;3)

(1;2;3) (1;1;3) (1;2;1)

(1;2;2)

(1;1;2)(1;2;1)(1;2;2) (1;1;1)(1;1;3)(1;2;3)

(1;2;2) (1;2;3) (1;2;1)

(3;2;2)

(1;1;2)(1;2;1)(3;2;2) (1;1;1)(1;1;3)(1;2;3)(1;2;2)

(3;2;2)

(1;2;2) (3;2;3)
(3;2;1)

(1;1;2)(1;2;1)(3;2;1) (1;1;1)(1;1;3)(1;2;3)(1;2;2)

(3;2;2)

(3;2;1)

(3;2;2) (3;2;3)
(3;3;1)

(1;1;2)(1;2;1)(3;3;1) (1;1;1)(1;1;3)(1;2;3)(1;2;2)

(3;2;2) (3;2;1)

(3;3;1)

(3;2;1) (3;3;2)
(3;3;3)

(1;1;2)(1;2;1)(3;3;3) (1;1;1)(1;1;3)(1;2;3)(1;2;2)

(3;2;2) (3;2;1) (3;3;1)

(3;3;3)

Lời giải của bài toán:

(1;1;1)

→

(1;1;3)

→

(1;2;3)

→

(1;2;2)

→

(3;2;2)

→

(3;2;1)

→

(3;3;1)

→

(3;3;3)

Cả hai ví dụ trên, chúng ta đều thấy, tìm kiếm theo chiều sâu đều cho lời

giải tốt và nhanh.
Ví dụ 3: Bài toán tìm dãy hợp lý với số hạng đầu a

= 26

Nhắc lại: Dãy a

, a

, …,a

được gọi là hợp lý nếu thoả hai điều kiện:

Trí tuệ nhân tạo

là số nguyên tố

k+1

= a

+1 hoặc 2*a

Như vậy, khi biết a

thì ta xác định được a

k+1

. Vì vậy có thể mô tả trạng

thái bài toán tương ứng với giá trj a

tại thòi điểm đang xét. Ta có thể chỉ ra một

cách tìm kiếm theo chiều sâu như sau

T(i)

↓↑

DONG

27 52

53 104

27 53 104

26 52

104

105 208

27 53 105 208

26 52 104

208

209 416

27 53 105 209 416

26 52 104 208

. . .

Với cách tìm kiếm theo theo thuật toán một cách máy móc như vậy thì rõ

ràng không bao giờ đạt được đích. Trong khi chúng ta dễ dàng nhận được lời
giải, chăng hạn:

= 26; a

= 52; a

= 53. Như vậy n =3.

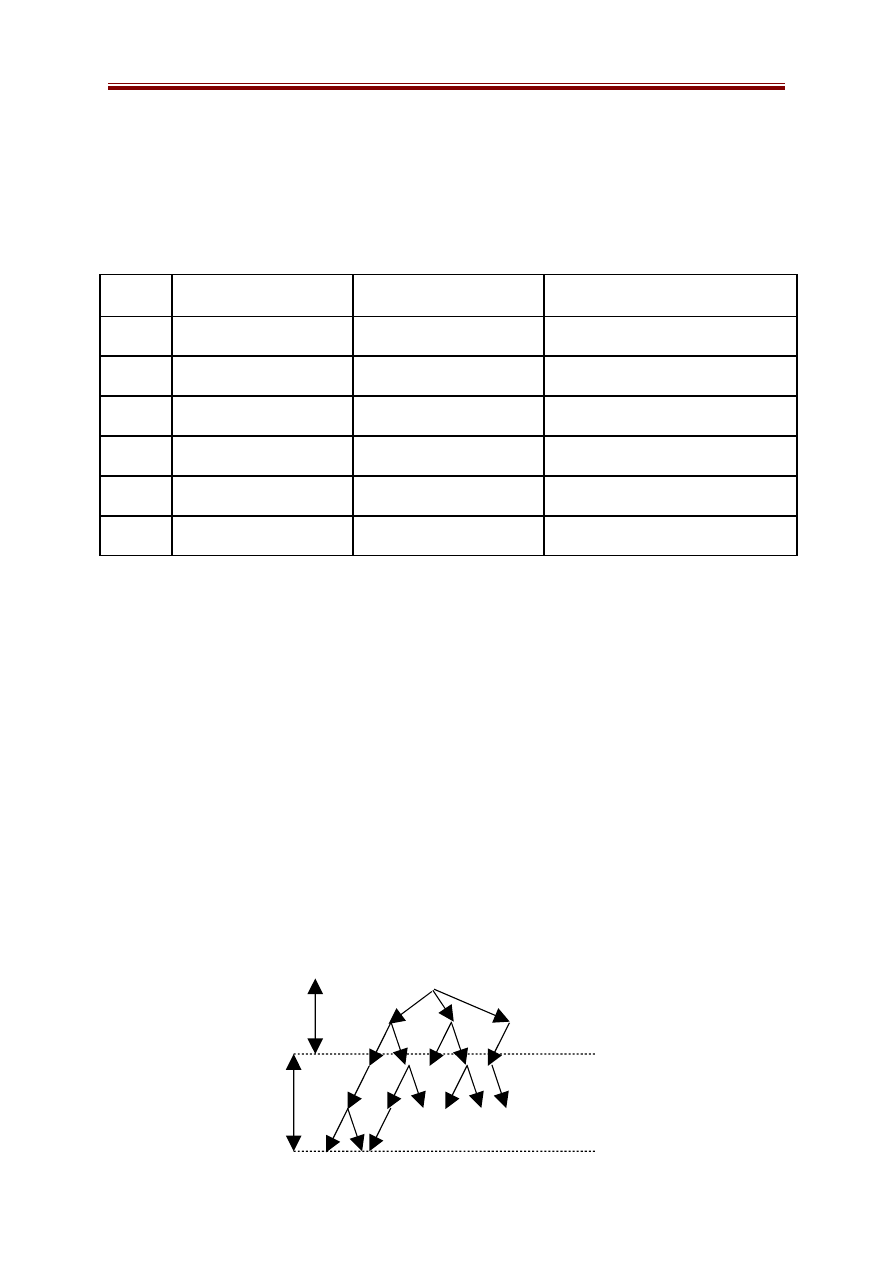
3.4. Phương pháp tìm kiếm theo chiều sâu dần

3.4.1. Kỹ thuật tìm kiếm sâu dần

Kỹ thuật tìm kiếm sâu dần là thực hiện việc tìm kiếm với độ sâu ở mức

giưói hạn d nào đó. Nếu không tìm ra nghiệm ta tăng độ sâu lên d+1 và lại tìm
kiếm theo độ sâu tới mức d+1. Quá trình trên được lặp lại với d lần lượt là 1,
2,...đến độ sâu max nào đó.

Kỹ thuật tìm kiếm sâu dần thường được thực hiện khi cây tìm kiếm chứa

nhánh vô hạn, và nếu sử dụng tìm kiếm theo độ sâu ta có thể mắc kẹt ở một
nhánh nào đó (thuật toán không dừng) và không tìm ra nghiệm.

Trí tuệ nhân tạo

3.4.2. Giải thuật

Thuật toán tìm kiếm sâu dần sử dụng thuật toán tìm kiếm sâu hạn chế như

thủ tục con. Đó là thủ tục tìm kiếm theo chiều sâu nhưng chỉ tới độ sâu d nào đó
rồi quay lên.

Thủ tục tìm kiếm sâu hạn chế (depth_limitedsearch)

Procedure Depth_limited_search(d);

{d là tham số độ sâu}

Begin

Push (MO,n

);

Depth(n

)=0;

{hàm depth ghi lại độ sâu mỗi

đỉnh}

DONG=null;

While MO <> null do

begin

n:=pop (MO);

if n

∈

DICH then exit;

push (DONG, n);

if depth(n)<=d then

For m

∈

T(n) and m

∉

DONG do

begin

Push (MO, m);

depth(m)=depth(n)+1;

end;

Write (‘Không có lời giải’);

End;

Trí tuệ nhân tạo

Thuật toán tìm kiếm sâu dần (Depth_deepening_search) sẽ sử dụng thủ

tục tìm kiếm sâu hạn chế như thủ tục con:

Procedure Depth_deepening_search;

Begin

For d:=0 to max do

Depth_limited_search(d);

If thành công then exit;

End;

3.4.3. Nhận xét

- Luôn tìm ra nghiệm (nếu bài toán có nghiệm), miễn là chọn max đủ lớn

(giống như tìm kiếm theo chiều rộng).

- Có độ phức tạp thời gian là O(kd) (giống tìm kiếm rộng).
- Có độ phức tạp không gian là O(k*d) (giống tìm kiếm sâu).
- Giải thuật tìm kiếm sâu dần thường áp dụng cho các bài toán có không

gian trạng thái lớn và độ sâu của nghiệm không biết trước.

Trí tuệ nhân tạo

B - TÌM KIẾM KINH NGHIỆM VÀ TỐI ƯU

(Tìm kiếm heuristic)

Kỹ thuật tìm kiếm mù là phương pháp cơ bản để khai thác không gian bài

toán. Chúng đều vét cạn không gian để tìm ra lời giải theo thủ tục xác định
trước. Mặc dù có sử dụng tri thức về trạng thái của bài toán để hướng dẫn tìm
kiếm nhưng không phổ biến, kém hiệu quả và trong nhiều trường hợp không thể
áp dụng được .

Như vậy, chúng ta sẽ nghiên cứu các phương pháp tìm kiếm kinh nghiệm

(tìm kiếm heuristic), đó là các phương pháp sử dụng hàm đánh giá để hướng
dẫn sự tìm kiếm.

* Hàm đánh giá và tìm kiếm kinh nghiệm:

Trong nhiều vấn đề, ta có thể sử dụng kinh nghiệm, tri thức của chúng ta

về vấn đề đó để đánh giá các trạng thái của vấn đề.

Với mỗi trạng thái u, ta sẽ xác dịnh một giá trị số h(u), số này đánh giá

“sự gần đích” của trạng thái u. Hàm h(u) được gọi là hàm đánh giá.

Phương pháp tìm kiếm kinh nghiệm là phương pháp tìm kiếm có sử dụng

đến hàm đánh giá.

Trong quá trình tìm kiếm, tại mỗi bước ta sẽ chọn trạng thái để phát triển

là trạng thái có giá trị hàm đánh giá nhỏ nhất, trạng thái này được xem là trạng
thái có nhiều hứa hẹn nhất hướng tới đích.

Quá trình tìm kiếm trong không gian trạng thái có sử dụng hàm đánh giá bao
gồm các bước cơ bản sau:

- Biểu diễn thích hợp các trạng thái và các toán tử chuyển trạng thái

- Xây dựng hàm đánh giá

- Thiết kế chiến lược chọn trạng thái ở mỗi bước

Hàm đánh giá

Trong tìm kiếm kinh nghiệm, hàm đánh giá đóng vai trò cực kỳ quan

trọng. Chúng ta có xây dựng được hàm đánh giá cho ta sự đánh giá đúng các
trạng thái thì tìm kiếm mới hiệu quả.

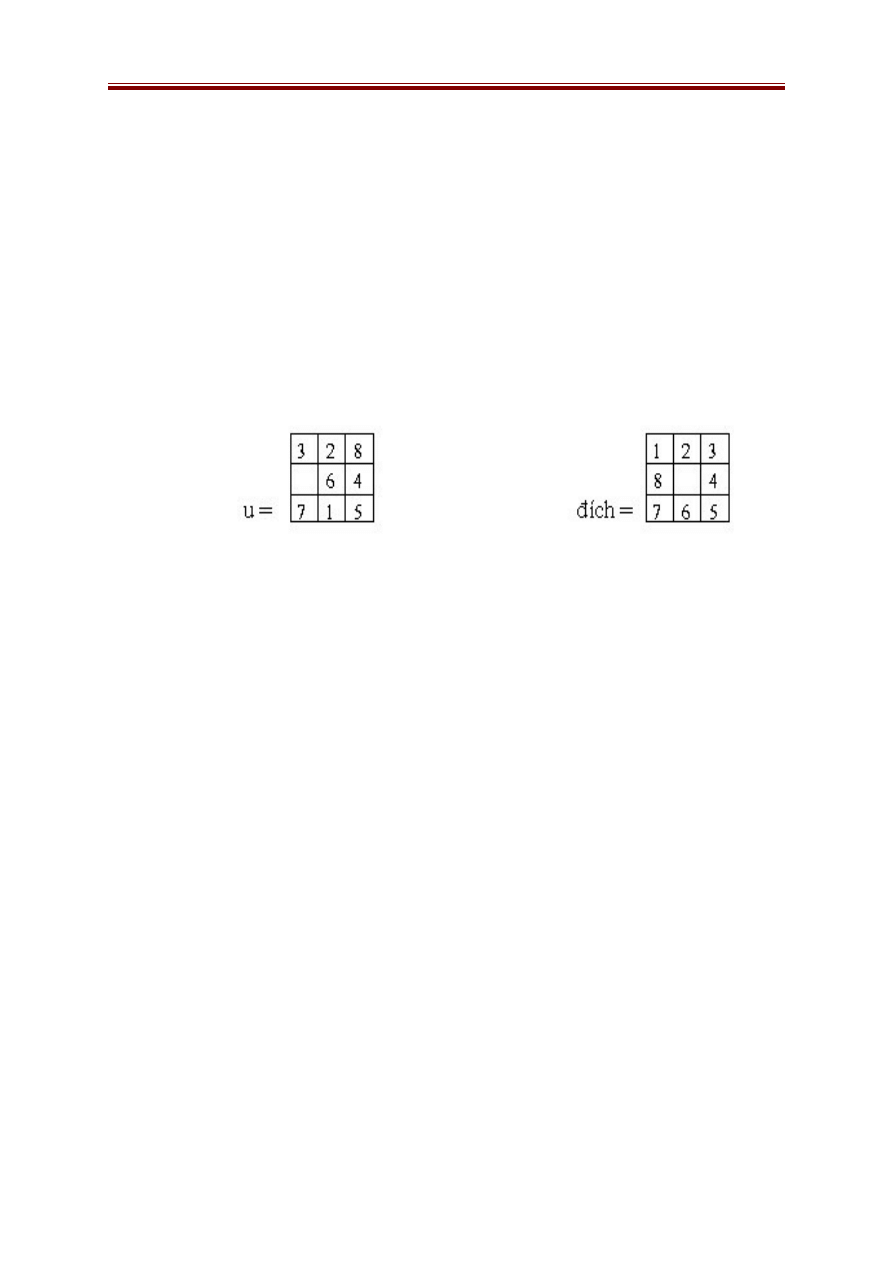
Trí tuệ nhân tạo

Nếu hàm đánh giá không chính xác, nó có thể dẫn ta đi chệch hướng và

do đó tìm kiếm kém hiệu quả.

Hàm đánh giá được xây dựng tùy thuộc vào vấn đề. Sau đây là một số ví

dụ về hàm đánh giá:

Ví dụ 1: Trong bài toán tìm kiếm đường đi trên bản đồ giao thông, ta có

thể lấy độ dài của đường chim bay từ một thành phố tới một thành phố đích làm
giá trị của hàm đánh giá.

Ví dụ 2: Bài toán 8 số.

Chúng ta có thể đưa ra hai cách xây dựng hàm đánh giá.

- Hàm h1: Với mỗi trạng thái u thì h1(u) là số quân không nằm đúng vị

trí của nó trong trạng thái đích, thì h1(u) = 4, vì các quân không đúng vị trí là 3,
8, 6 và 1.

- Hàm h2: Gọi h2(u) là là tổng khoảng cách giữa vị trí của các quân

trong trạng thái u và vị trí của nó trong trạng thái đích (khoảng cách được hiểu
là số lần dịch chuyển ít nhất theo hàng hoặc cột để đưa một quân ở vị trí của
hiện tại tới trạng thái đích).

Ta có: h2(u)=2+3+1+3= 9 (vì quân 3 cần ít nhất 2 dịch chuyển, quân 8

cần ít nhất 3 dịch chuyển, quân 6 cần ít nhất 1 dịch chuyển và quân 1 cần ít nhất
3 dịch chuyển).

Tìm kiếm kinh nghiệm

Hai chiến lược tìm kiếm kinh nghiệm quan trọng nhất là tìm kiếm tốt nhất

- đầu tiên (Best-First Search) và tìm kiếm leo đồi (Hill-Climbing Search). Có
thể xác định các chiến lược này như sau:

Trí tuệ nhân tạo

- Tìm kiếm tốt nhất đầu tiên = Tìm kiếm theo bề rộng

+ Hàm đánh

giá

- Tìm kiếm leo đồi

= Tìm kiếm theo độ sâu

+ Hàm đánh

giá

3.5. Kỹ thuật tìm kiếm tốt nhất đầu tiên (Best First Search)

3.5.1. Kỹ thuật tìm kiếm tốt nhất đầu tiên

Sử dụng hàm đánh giá để hướng dẫn việc tìm kiếm. Hàm này dùng các

thông tin hiện tại về mức độ quan trọng của bài toán tại nút đó để gán giá trị cho
nút này, gọi là trọng số của nút. Giá trị này được xem xét trong lúc tìm kiếm.
Thông thường, nút có trọng số nhỏ (lớn) nhất sẽ được chọn trong quá trình tìm
kiếm.

Tìm kiếm tốt nhất đầu tiên khác với tìm kiếm theo chiều rộng ở chỗ:

- Trong tìm kiếm theo chiều rộng ta lần lượt phát triển tất cả các nút ở

mức hiện tại để sinh ra các nút ở mức tiếp theo.

- Còn trong tìm kiếm tốt nhất đầu tiên ta chọn nút để phát triển là nút tốt

nhất được xác định bởi hàm đánh giá (tức là nút có có trọng số nhỏ (lớn) nhất sẽ
được chọn), nút này có thể ở mức hiện tại hoặc ở các mức trên.

3.5.2. Ưu và nhược điểm của phương pháp tìm kiếm tốt nhất đầu tiên

* Ưu điểm:

- Phương pháp tìm kiếm tốt nhất đầu tiên tổ hợp các ưu điểm của phương

pháp tìm kiếm rộng và tìm kiếm sâu.

- Ưu điểm chủ yếu của phương pháp tìm kiếm tốt nhất đầu tiên là dùng tri

thức để dẫn dắt việc tìm kiếm. Tri thức này giúp người ta bắt đầu từ đâu là tốt
nhất và cách tốt nhất để tiến hành tìm lời giải.

- Tìm kiếm tốt nhất đầu tiên tuân theo cách suy lý của một chuyên gia.

Do đó có thể thấy rõ đường đi hơn tìm kiếm rộng và tìm kiếm sâu.

* Nhược điểm:

Trí tuệ nhân tạo

- Quá trình tìm kiếm có thể đi xa khỏi lời giải. Kỹ thuật này chỉ xét một

phần của không gian và coi đó là phần hứa hẹn hơn cả.

3.5.3. Giải thuật

Dữ liệu tương tự như giải thuật tìm kiếm rộng và sâu, sử dụng danh sách

MO để lưu các đỉnh sẽ xét.

Procedure BFS; {Best First Search}

Begin

Push(MO,n

);

while MO <> null do

begin

i := Pop(MO);

if i

∈

Goals then

exit;

for j

∈

T(i) do

Push(MO,j);

Sort(MO); {theo thứ tự của hàm đánh giá}

end;

write(‘Khong co loi giai’);

end;

3.5.4. Ví dụ

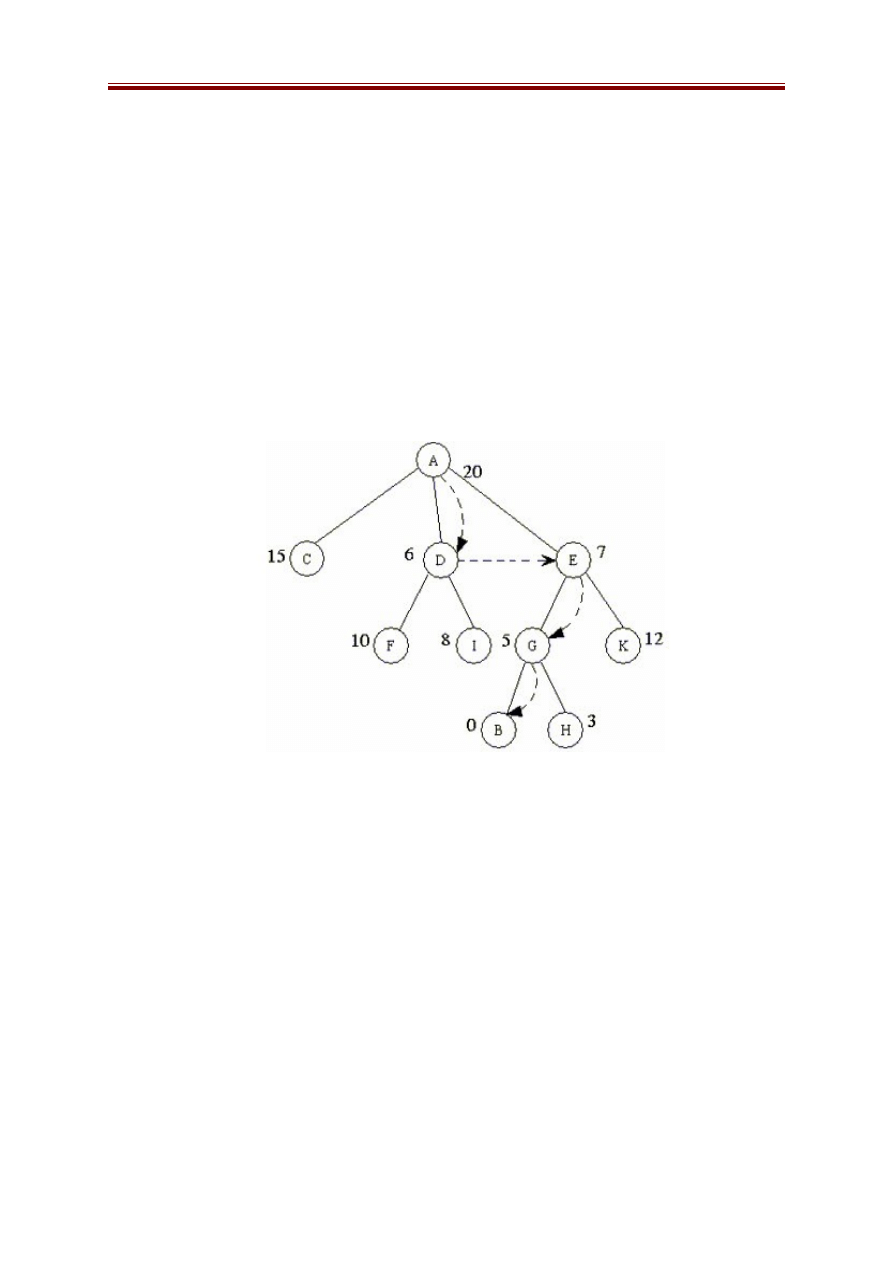
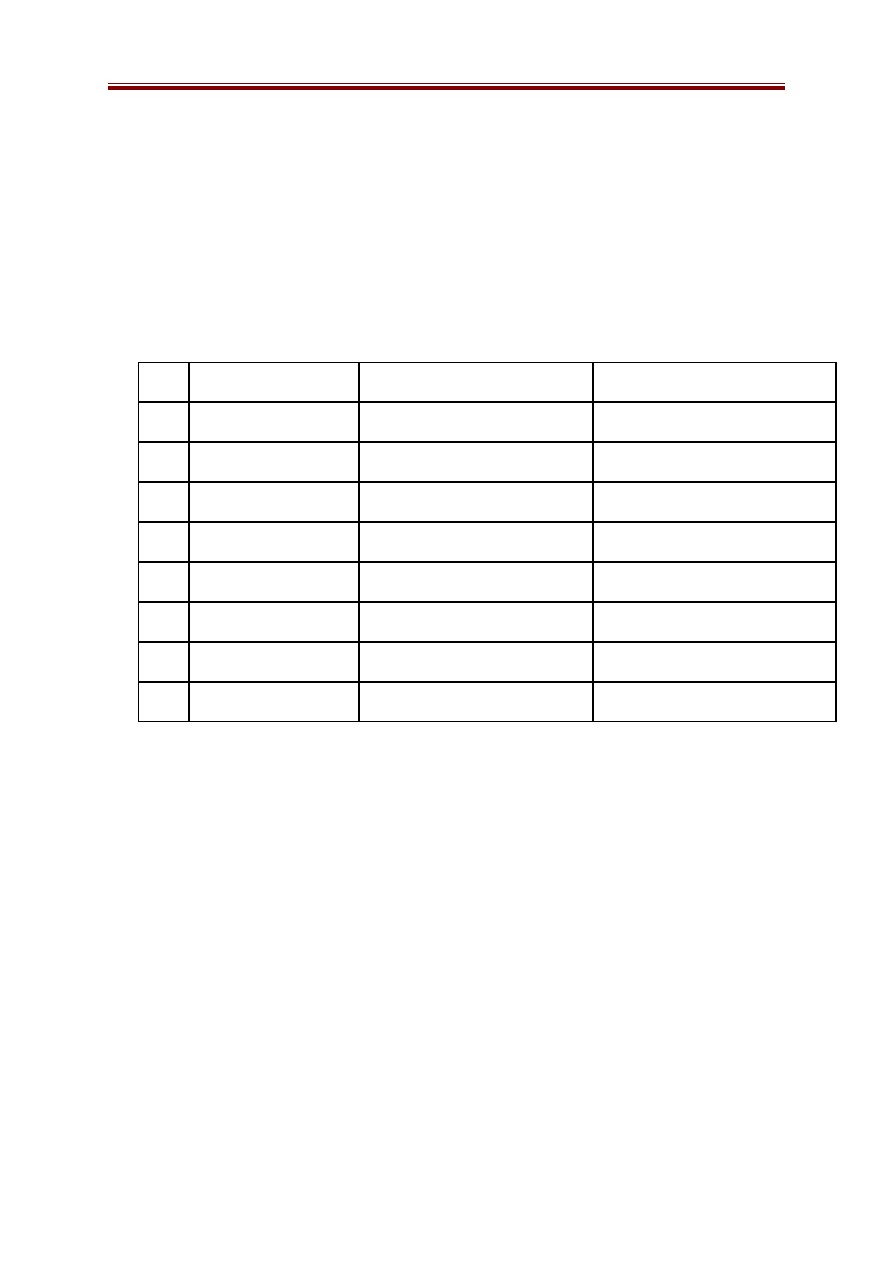
Xét không gian trạng thái được biểu diễn bởi đồ thị trong hình sau, trong

đó trạng thái ban đầu là A, trạng thái kết thúc là B. Giá trị của hàm đánh giá là
các trọng số ghi cạnh mỗi nút.

danh sách MO được sắp theo thứ tự
tăng dần của hàm đánh giá (hay
trọng số)

Trí tuệ nhân tạo

* Quá trình tìm kiếm tốt nhất đầu tiên diễn ra như sau:

- Đầu tiên phát triển nút A sinh ra các nút kề là C, D và E. Trong ba nút

này, nút D có giá trị hàm đánh giá nhỏ nhất, nó được chọn để phát triển và sinh
ra F, I.

- Trong số các nút chưa được phát triển C, E, F, I thì nút E có giá trị đánh

giá nhỏ nhất, nó được chọn để phát triển và sinh ra các đỉnh G, K.

- Trong số các nút chưa được phát triển thì G tốt nhất, phát triển G sinh ra

B, H. Đến đây ta đã đạt tới trạng thái kết thúc.

Kết quả:

3.6. Phương pháp tìm kiếm leo đồi (Hill-Climbing Search)

3.6.1. Kỹ thuật tìm kiếm leo đồi

Tìm kiếm leo đồi là tìm kiếm theo độ sâu được hướng dẫn bởi hàm đánh

giá.

Trí tuệ nhân tạo

Song khác với tìm kiếm theo độ sâu, khi phát triển một đỉnh u thì bước

tiếp theo ta chọn trong số các đỉnh con của u, đỉnh có hứa hẹn nhiều nhất để
phát triển, đỉnh này được xác định bởi hàm đánh giá.

3.6.2. Nhận xét phương pháp tìm kiếm leo đồi

Phương pháp tìm kiếm leo đồi chú trọng tìm hướng đi dễ dẫn đến trạng

thái đích nhất. Vấn đề quan trọng là biết khai thác khéo léo thông tin phản hồi
để xác định hướng đi tiếp và đẩy nhanh quá trình tìm kiếm.

Thông thường ta gán mỗi trạng thái của bài toán với một số đo (hàm đánh

giá) nào đó nhằm đánh giá mức độ gần đích của nó. Điều đó có nghĩa là nếu
trạng thái hiện thời là u thì trạng thái v sẽ được phát triển tiếp theo nếu v kề với
u và hàm đánh giá của v đạt giá trị max (hoặc min).

Tuy nhiên phương pháp này không được cải thiện so với các phương

pháp khác trong một số trường hợp sau:

- Cực trị địa phương: nút đang xét tốt hơn các nút lân cận, nhưng đó

không phải là phương án tốt nhất trong toàn thể, ví vậy có thể phải quay lui về
nút trước để đi theo hướng khác. Giải pháp này đòi hỏi ghi nhớ lại nhiều đường
đi.

- Cao nguyên bằng phẳng: Các giá trị của các phương án như nhau,

không xác định được ngay hướng nào là tốt hơn trong vùng lân cận.

3.6.3. Giải thuật

Input:

Đồ thị G = (V,E), đỉnh xuất phát n

Hàm đánh giá h(n) đối với mỗi đỉnh n.

Tập đỉnh đích DICH.

Output:

Đường đi từ đỉnh n

đến DICH.

Procedure HLC; {Hill Climbing Search}

begin

Trí tuệ nhân tạo

Push(MO,n

);

while MO <> null do

begin

i = Pop(MO);

if T(i)

∩

DICH <> null then

begin

L:= null;

for j

∈

T(i) do

if j chưa xét then

đưa j vào danh sách L

sắp xếp L theo thứ tự hàm đánh giá;

chuyển danh sách L vào đầu danh sách MO;

end;

write(‘Khong co loi giai’);

end;

Dữ liệu tương tự như giải thuật tìm kiếm sâu, sử dụng danh sách MO để

lưu các đỉnh sẽ xét.

3.6.4. Các ví dụ

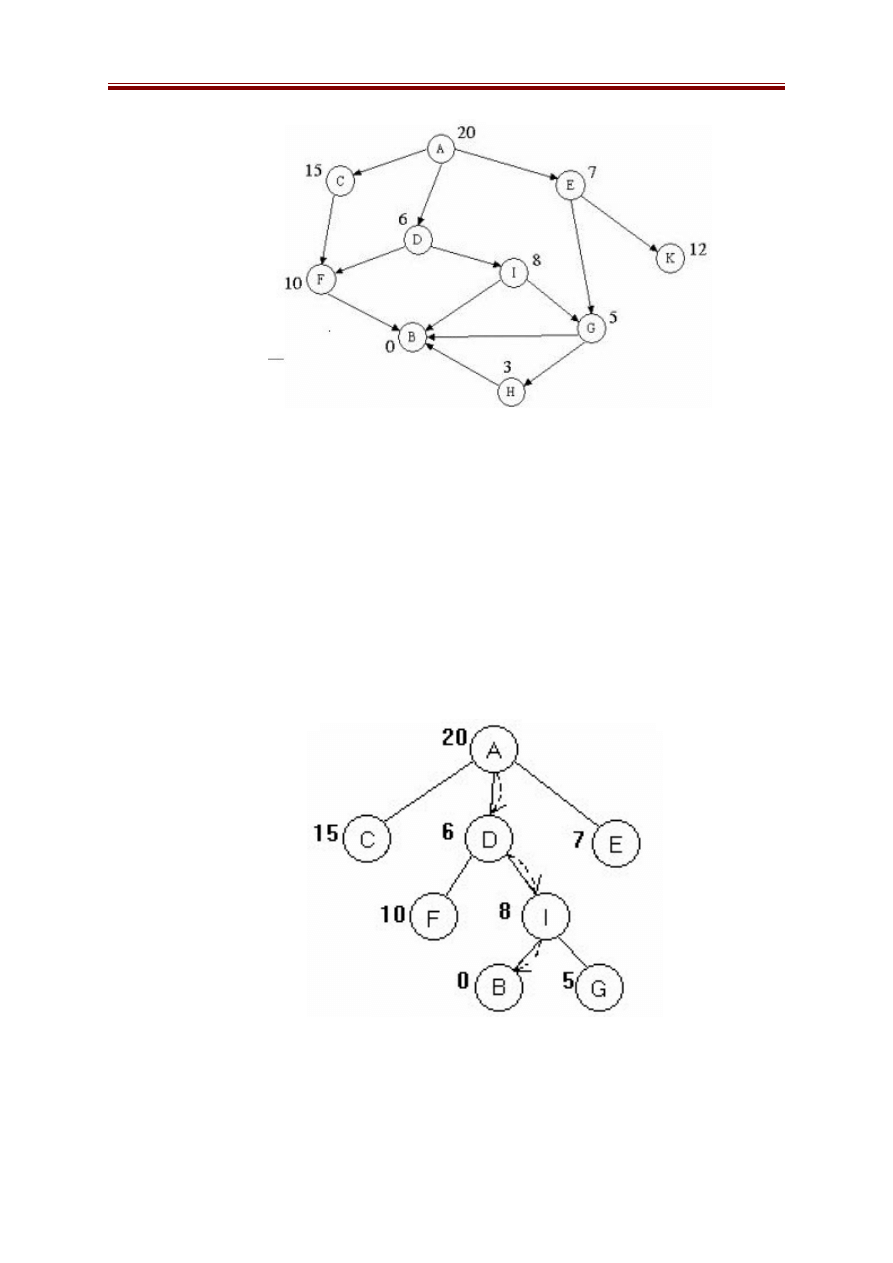
Ví dụ 1: Xét không gian trạng thái được biểu diễn bởi đồ thị trong hình

sau, trong đó trạng thái ban đầu là A, trạng thái kết thúc là B. Giá trị của hàm
đánh giá là các trọng số ghi cạnh mỗi nút.

Trí tuệ nhân tạo

* Quá trình tìm kiếm leo đồi diễn ra như sau:

Đầu tiên phát triển đỉnh A sinh ra các đỉnh con C, D, E. Trong các đỉnh

này chọn D để phát triển, và nó sinh ra các đỉnh con B, G. Quá trình tìm kiếm
kết thúc. Cây tìm kiếm leo đồi được cho trong hình dưới đây:

Trí tuệ nhân tạo

Ví dụ 2: Bài toán trò chơi 8 số

Trạng thái được chọn đi tiếp ở hướng mũi tên.

Ở mức 3 chúng ta thấy có hai trạng thái cùng giá trị hàm đánh giá (h = 3).

Đây là trương hợp “cao nguyên băng phẳng” như nhận xét trên, nếu ta chọn
phương án kia thì chắc chắn quá trình tìm kiếm sẽ khác đi nhiều.

Minh hoạ cây tìm kiếm cho trò chơi này theo giải thuật leo đồi với hướng

chọn như sau:

Trí tuệ nhân tạo

2 8 3

1 6 4

h(u) = 4

2 8 3

1 6 4

7 5

7 6 5

7 5

h(u) = 5 h(u) = 3

h(u) = 5

2 8 3

1 4

1 8 4

1 4

7 6 5

h(u) = 3 h(u) = 3

h(u) = 4

2 3

1 8 4

7 6 5

h(u) = 2 h(u) = 4

Trí tuệ nhân tạo

1 2 3

8 4

7 6 5

h(u) = 1

1 2 3

7 6 5

3.7. Tìm kiếm đường đi có giá thành cực tiểu - Thuật giải AT

3.7.1. Đặt vấn đề

Cho đồ thị G= (V, E) biểu diễn bài toán với đỉnh xuất phát n

và tập đích

DICH xác định.

Với mỗi phép chuyển trạng thái n

→

i+1

tốn chi phí c(n

, n

i+1

) ký hiệu c(u)

với u= (n

, ni

)

∈

c(u)

i+1

* Vấn đề:

Tìm đường đi p: n

∈

DICH sao cho

min

)

(

)

(

→

∑

∈

(Giá của đường đi là tổng giá các cung tham gia vào đường đi và vấn đề

là tìm đường đi có giá min).

Chẳng hạn trong bài toán tìm đường đi trong bản đồ giao thông, giá của

cung (i,j) chính là độ dài của đường nối thành phố i với thành phố j. Độ dài
đường đi được xác định là tổng độ dài các cung trên đường đi. Vấn đề đặt ra là
tìm đường đi ngắn nhất từ trạng thái ban đầu đến trạng thái đích.

Trí tuệ nhân tạo

* Phương pháp giải

- Nếu

const

∈

∀

)

(

)

(

thì

min

)

(

→

⇔

→

⇒

Dùng phương

pháp tìm kiếm theo chiều rộng.

- Gọi g(n) là giá của đường đi cực tiểu từ đỉnh n

đến n, khi đó bài toán có

thể phát biểu như sau:

* Tìm đường đi từ đỉnh

DICH

∈

→

sao cho:

{

}

DICH

∈

)

(

min

)

(

Lúc đó, ta có:

)

(

{

}

)

(

)

(

min

)

(

)

(

∈

Dùng 2 danh sách MO, DONG như trên. Tại mỗi thời điểm chọn đỉnh n

trong MO ra xét là đỉnh thoả.

3.7.2. Thuật giải AT

Input:

Đồ thị G = (V,E), Đỉnh xuất phát n

Hàm chi phí c: E

→

c(i,j): xác định chi phí chuyển từ đỉnh i sang đỉnh j với (i,j)

∈

Tập các đỉnh đích DICH

Output:

Đường đi từ đỉnh n

đến đỉnh n

∈

DICH sao cho g(n

) = c(p) = min{g(n)|

∈

DICH}.

Procedure AT;

{ Dùng g

(n) là chi phí cực tiểu của đường đi từ đỉnh xuất phát đến đỉnh n tại

thời điểm đang xét và xem như hàm g}

Begin

g(n

):= 0;

push(MO, n

);

Trí tuệ nhân tạo

While MO<>null do

begin

)

(

min

)

(

∈

if n

∈

DICH then

exit {xay dung duong di cuc tieu}

push(DONG, n);

if T(n) <>null then

for m

∈

T(n) do

if m

∉

MO+DONG then

begin

push(MO,m);

g(m):=g(n)+c(n,m);

cha(m):=n;

end

else

if g(m) >g(n)+c(n,m) then

begin

g(m):=g(n)+c(n,m);

cha(m):=n;

end;

writeln(‘Khong co duong di’);

End;

3.7.3. Các ví dụ

Trí tuệ nhân tạo

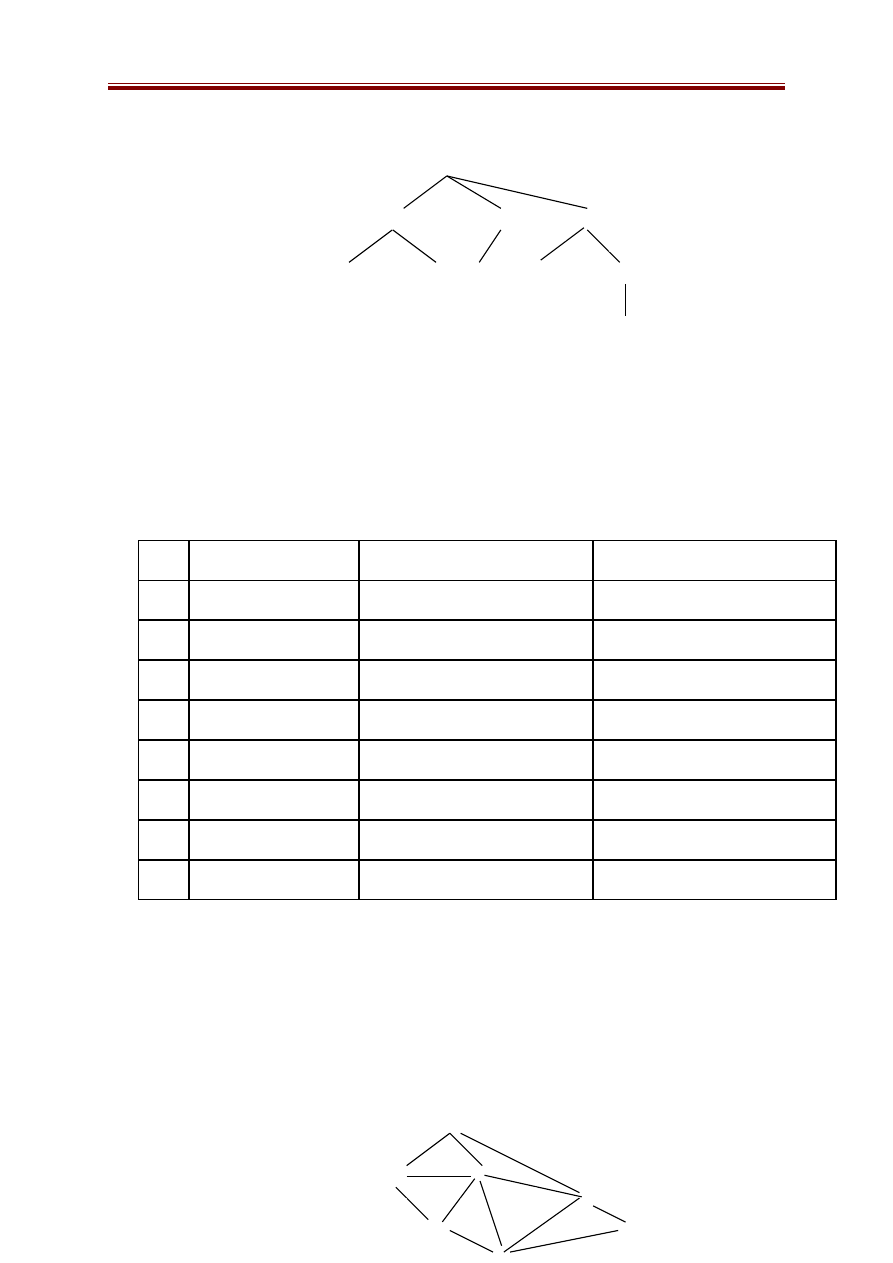
Ví dụ 1:

DICH={F,K}

F G

Có thể trình bày quá trình tìm kiếm bằng bảng dưới đây. Ký hiệu giá trị

g(n) là chỉ số dưới tương ứng đỉnh n: n

g(n)

T(i)

DONG

B C D

A C

H I

A C D

A C D G

A C D G I

E F

A C D G I B

Lời giải của bài toán là A

→

K và chi phí của đường đi tìm được

là 8

Ví dụ 2:

= A; DICH = {G}

Trí tuệ nhân tạo

T(i)

DONG

B C D

A B E F D

A C

A C E

A C B

A C F G

A C B D

B C F

A C B D E

C D E G

A C B D E F

Đường đi tìm được p: A

→

G. Chi phí của đường đi là 14.

Ví dụ 3: Bài toán Tháp Hà Nội - với chi phí chuyển đĩa như sau:

Chi phí chuyển đĩa nhỏ giữa 2 cọc gần

Chi phí chuyển đĩa nhỏ giữa 2 cọc xa

Chi phí chuyển đĩa vừa giữa 2 cọc gần

Chi phí chuyển đĩa vừa giữa 2 cọc xa

Chi phí chuyển đĩa lớn giữa 2 cọc gần

Chi phí chuyển đĩa lớn giữa 2 cọc xa

Trí tuệ nhân tạo

Xuất phát từ đỉnh (1,1,1), ta có g(1,1,1) = 0.
Khi xét đỉnh (1,1,1) ta có các đỉnh kề và chi phí tương ứng :

g(1,1,2) = 1; g(1,1,3) = 3; như vậy đỉnh (1,1,2) được chọn

Các đỉnh kề của (1,1,2) có giá trị hàm g:

g(1,1,3) = 2 (ở đây giá của đỉnh (1,1,3) được tính lại); g(1,3,2) = 5; chọn

đỉnh (1,1,3), ta lại tính tiếp giá trị hàm g của các đỉnh kề với đỉnh này:

g(1,2,3) = 2; lại chọn đỉnh (1,2,3); chi phí của các đỉnh kề với nó:

g(1,2,1) = 2 + 3 = 5; g(1,2,2) = 2 + 1 = 3; chọn đỉnh (1,2,2)

g(1,2,1) = 3 +1 = 4 (được tính lại); g(3,2,2) = 3 + 8 = 11, chọn đỉnh

(1,2,1)

Cứ tiếp tục như vậy cho đến khi xét đỉnh (3,3,3).

3.8. Tìm kiếm đường đi cực tiểu - Thuật giải A*

3.8.1. Đặt vấn đề

Đối với nhiều bài toán, việc tìm kiếm đường đi cực tiểu sẽ được định

hướng tập trung xung quanh đường đi tốt nhất, nếu sử dụng các thông tin đặc tả
về bài toán gọi là các heuristic.

Đối với việc tìm kiếm đường đi với chi phí cực tiểu, người ta sử dụng

hàm đánh giá heuristic như sau:

- Gọi g(n): giá cực tiểu đường đi từ n0

→

n. Tại đỉnh n, g(n) xác định được.

- Gọi h(n): giá cực tiểu đường đi từ n

→

DICH, h(n) không xác định được

⇒

người ta tìm cách ước lượng giá trị này.

Để làm giảm không gian tìm kiếm ta dựa vào heuristic để ước lượng giá

trị các nút.

Đặt f0(n)=g0(n)+h0(n): dự đoán chi phí cực tiểu của đường đi từ

→

DICH có đi qua đỉnh n.

Trong đó:

Trí tuệ nhân tạo

+ g0(n) là chi phí của đường đi từ đỉnh xuất phát đến đỉnh n tại thời điểm

đang xét

(hay là giá trị ước lượng dựa trên sự khai thác thông tin kinh nghiệm

quá khứ).

+ h0(n) là ước lượng (dự đoán) chi phí đường đi từ đỉnh n đến đích (hay

là giá trị ước lượng dựa trên sự khai thác thông tin của nút hướng tới tương lai).

Việc chọn giá trị xấp xỉ h0(n) của h(n) không có một phương pháp tổng quát và
được xem như một nghệ thuật, giá trị này sẽ do các chuyên gia đưa ra.

Chỉ số “0” ám chỉ đây là giá trị ước lượng chứ không phải giá trị chính

xác. Giá trị chính xác chỉ biết được khi ta đến đích tức giải xong bài toán.

Ta chú ý h0(n) càng lớn thì càng tốt, tức là khai thác nhiều thông tin về

trạng thái hiện tại hướng tới tương lai.

Tuy nhiên người ta CM được rằng thuật toán A* chắc chắn dừng khi

h0(n) <= h(n) (h0=h: phương án tốt nhất, h0=0: phương án tồi nhất).

Lúc này giải thuật tìm kiếm cực tiểu sẽ thay việc xét hàm g (như đã biết

mục trước) bởi hàm f.

3.8.2. Thuật giải A*

Input:

Đồ thị G = (V,E), Đỉnh xuất phát n

Hàm chi phí c: E

→

c(i,j): xác định chi phí chuyển từ đỉnh i sang đỉnh j với (i,j)

∈

h: V

→

; h(n) xác định dự đoán chi phí tối ưu của đường đi từ đỉnh n

đến đích. (ký hiệu h thay cho h

, (tương tự g))

Tập các đỉnh đích DICH

Output:

Đường đi từ đỉnh n

đến đỉnh n

∈

DICH

Procedure A

;

Trí tuệ nhân tạo

Begin

g(n

):= 0;

push(MO, n

);

While MO<>null do

begin

)

(

min

)

(

∈

if n

∈

DICH then

exit {xay dung duong di cuc tieu}

push(DONG, n);

if T(n) <>null then

for m

∈

T(n) do

if m

∉

MO+DONG then

begin

push(MO,m);

tính f(m);

cha(m):=n;

end

else

if f

mới

(m) > f

cũ

(n) then

begin

f(m):= f

mới

(m);

cha(m):=n;

end;

Trí tuệ nhân tạo

writeln(‘Khong co duong di’);

End;

3.8.3. Các ví dụ

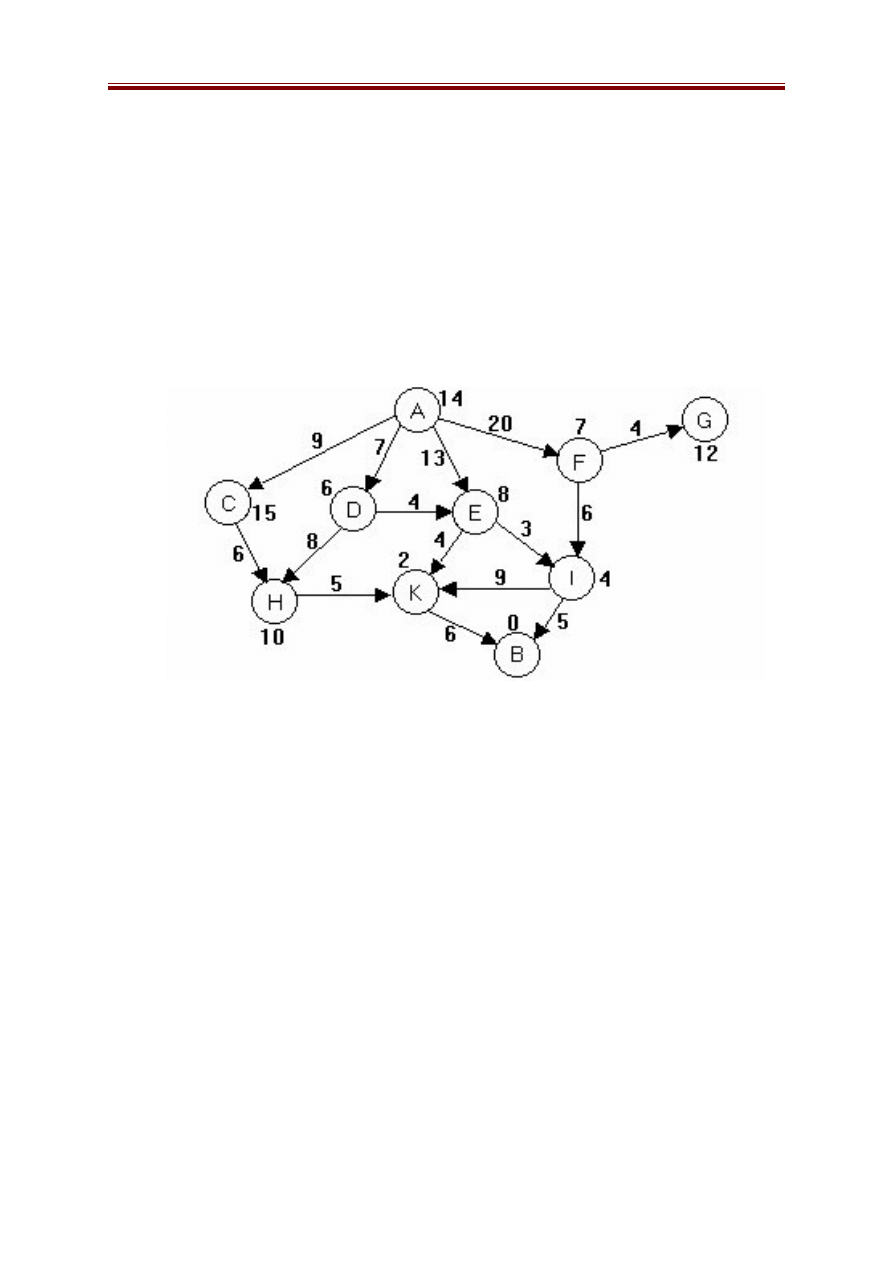
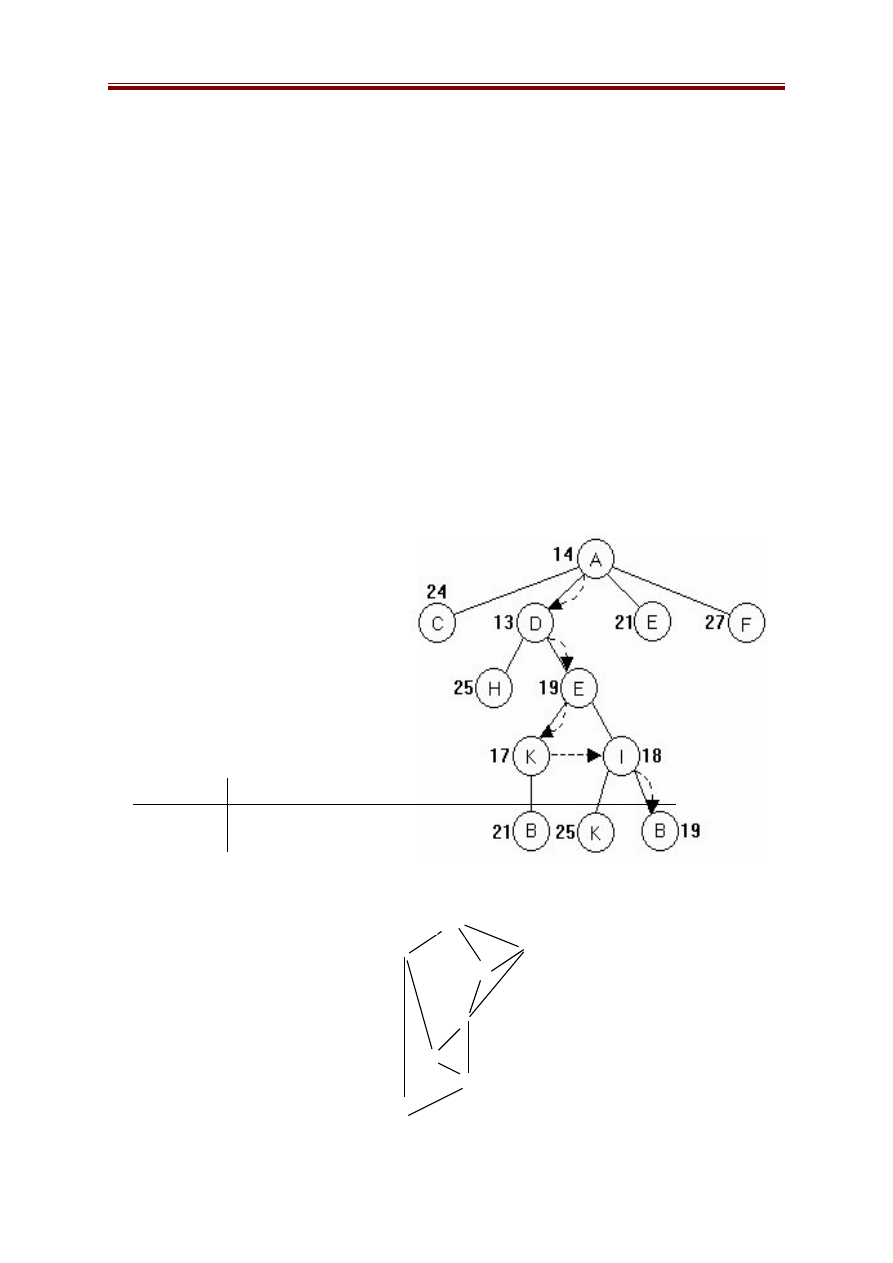
Ví dụ 1:

Trạng thái ban đầu là trạng thái A, trạng thái đích là B, các số ghi cạnh

các cung là độ dài đường đi, các số cạnh các đỉnh là giá trị của hàm h

Đầu tiên, phát triển đỉnh A sinh ra các đỉnh con C, D, E và F. Tính giá trị

của hàm f tại các đỉnh này ta có:

g(C) = 9, f(C) = 9 + 15 = 24, g(D) = 7, f(D) = 7 + 6 = 13

g(E) = 13, f(E) = 13 + 8 = 21, g(F) = 20, f(F) = 20 +7 = 27

Như vậy đỉnh tốt nhất là D (vì f(D) = 13 là nhỏ nhất). Phát triển D, ta

nhận được các đỉnh con H và E. Ta đánh giá H và E (mới):

g(H) = g(D) + Độ dài cung (D, H) = 7 + 8 = 15, f(H) = 15 + 10 = 25.

Đường đi tới E qua D có độ dài:

Trí tuệ nhân tạo

g(E) = g(D) + Độ dài cung (D, E) = 7 + 4 = 11.

Vậy đỉnh E mới có đánh giá là f(E) = g(E) + h(E) = 11 + 8 = 19.

Trong số các đỉnh cho phát triển, thì đỉnh E với đánh giá f(E) = 19 là đỉnh

tốt nhất. Phát triển đỉnh này, ta nhận được các đỉnh con của nó là K và I.

Chúng ta tiếp tục quá trình trên cho tới khi đỉnh được chọn để phát triển

là đỉnh kết thúc B, độ dài đường đi ngắn nhất tới B là g(B) = 19. Quá trình tìm
kiếm trên được mô tả bởi cây tìm kiếm sau, trong đó các số cạnh các đỉnh là các
giá trị của hàm đánh giá f.

KL: A  D  E  I  B

Ví dụ 2: Cho đồ thị biểu diễn bài toán và giá trị dự đoán h

như sau:

(n)

(4;3)

(0;3)

(4;0)

(3;0)

(1;3)

(3;3)

(0;3)

(0;2)

(4;2)

(4;1)

(2;0)

(2;3)

Trí tuệ nhân tạo

Tìm đường đi từ đỉnh A đến đỉnh H.

Trước tiên đỉnh A được đưa vào danh sách MO

g(A) = 0; h(A) = 14; f(A) = 14

Xét đỉnh A, (đưa A vào danh sách DONG) ta có các đỉnh kề B, C, D:

g(B) = 5; f(B) = 15; g(C) = 3; f(C) = 13; g(D) = 7; f(D) = 12  chọn

đỉnh D.

Xét đỉnh D (đưa D vào danh sách DONG) có các đỉnh kề A, C, E. Đỉnh A

đã ở trong danh sách DONG, ta tính lại f(C) và tính f(E):

f(C) không thay đổi; f(E) = g(D) +c(D,E) + H(E) = 7 + 6 + 5 = 18; f(E) =

18, chọn đỉnh C, có các đỉnh kề A, D, E.

Tính lại f(E) = 12, chọn E. Các đỉnh kề của E là C, D, F, G.

Tính f(F) = 14; f(G) = 16, chọn F. Các đỉnh kề của F là E, G, B và f(B),

f(G) không đổi, chọn B. Các đỉnh kề của B là F, H. f(H) = 17, chọn G. Tính lại
f(H) = 15 và dừng.

Đường đi tìm được là p: A  C  E  G  H với chi phí đường đi là

15.

Ví dụ 3: Cho 1 bình dung tích 4 lít, 1 bình dung tích 3 lít. Làm thế nào để bình
4 có 2 lít.

Bài toán trở thành (4,3) (2,y)

Cho h: độ lệch của mức nước hiện có trong bình 4lít so với đích (2lít).

g: là độ dài mức đường đi từ nút gốc tới n

Ta có thể biểu diễn dưới dạng đồ thị sau:

(4;3)

(0;3)

(4;0)

(3;0)

(1;3)

(3;3)

(0;3)

(0;2)

(4;2)

(4;1)

(2;0)

(2;3)

Trí tuệ nhân tạo

3.9. Phương pháp sinh và thử

Chiến lược này đơn giản, gồm ba bước:

Trước hết tạo ra một giải pháp. Trong vài bài toán cụ thể đó là việc
chọn một lời giải trong không gian các lời giải hay tạo ra một đường đi.

Thứ hai, thử xem lời giải đó có thích hợp không bằng cách so sánh
phương án khác hay so sanh với điểm cuối cần suy diễn.

Tiếp theo, nếu lời giải đạt được thì dừng, ngước lại, lặp lại từ bước
đầu với nút khác.

Với phương pháp này nếu bài toán có lời giải thì sẽ đưa đến đích. Tuy

nhiên kích thước bài toán lớn sẽ tăng khối lượng tính toán. Việc tạo lời giải ban
đầu có thể thực hiện ngẫu nhiên, và cũng hy vọng ngẫu nhiên mà đạt được lời
giải, bởi vậy, không thể không tính đến chỉ một vài hướng đi được cảm nhận là
tốt, và loại trừ trước các hướng không dẫn đến lời giải.

Ví dụ 1: Tìm số có 6 chữ số mà tổng bình phương các chữ số chia hết

cho3.

(4;3)

(0;3)

(4;0)

(3;0)

(0;0)

(1;3)

(0;0) (4;3)

(0;0)

(4;0)

(3;3)

(0;3)

(4;3)

(1;0)

(4;0)

(0;3)

(4;3)

(3;0)

(0;0)

(4;0)

(1;3)

(0;1)

(4;3)

(0;2)

(4;0) (3;3)

g=1

g=2

g=3

g=4

Đích

g=0

(4;2)

(0;3)

(4;1)

(0;0) (1;0)

(0;3)

(4;2)

(0;0)

(2;0)

(4;3)

(0;1)

(4;0)

(2;3)

Đích

g=5

g=6

h=2

h=1

h=2

h=0

h=2

(4;3)

Trí tuệ nhân tạo

Giai đoạn sinh: tạo ra số có 6 chữ số và ta gọi các chữ số từ trái qua phải

lần lượt là a, b, c, d, e, f thì 0 < a <= 9 , 0 <= b, c, d, e, f <= 9.

Giai đoạn thử: nểu a*a + b*b + c*c + d*d + e*e + f*f chia hết cho 3 thì

chon, ngược lại, tạo ra số khác.

Ví dụ 2: Một bệnh nhân có một vài triệu chứng, chẳng hạn: sốt cao về

buổi chiều, ho và mệt mỏi ,…. Bác sĩ có chẩn đoán nghi bị lao phổi, người ta sẽ
cho làm ngay xét nghiệm, nếu đúng là dương tính thì kết luận và điều trị bệnh
lao phổi, ngược lai, bắt buộc bác sĩ phải chuyển hướng suy nghĩ sang một bệnh
khác, v.v…

3.10. Phương pháp thoả mãn ràng buộc

Phương pháp thoả mãn ràng buộc hỗ trợ cho phương pháp sinh và thử,

khi chú ý tới một số ràng buộc áp đặt lên các nút trong không gian bài toán.
Mục đích đặt ra là xác định đường đi trong đồ thị không gian bài toán, đường đi
từ trạng thái đầu đến trạng thái cuối đáp ứng một vài ràng buộc nào đó. Do vậy
quá trình tìm kiếm lời giải bao gồm hai phần liên quan chặt chẽ với nhau:

Tìm kiếm trong không gian các ràng buộc.

Tìm kiếm trong không gian các bài toán ban đầu.

Nội dung của phương pháp như sau: Thực hiện các bước từ a) đến e) dưới

đây cho đến khi tìm được lời giải đày đủ của bài toán hoặc tất cả các đương đều
đã duyệt qua nhưng không cho kết quả.

a) Chọn một đỉnh chưa được xét trong đồ thị tìm kiếm.
b) Áp dụng các luật suy diễn trên các ràng buộc đối với đỉnh đã chọn để

tạo ra tập các ràng buộc mới.

c) Nếu tập các ràng buộc mới có mâu thuẫn thì đưa ra thông báo đường

đi hện thời tới nút đang xét dẫn tới bế tắc.

d) Nếu tập ràng buộc mô tả lời giải đầy đủ của bài toán thì dừng và đưa

ra thông báo thành công. Ngược lai, sang bước sau.

e) Áp dụng các luật biến đổi không gian trạng thái tương ứng để tạo ra

lời giải bộ phận, tương hợp với tập các ràng buộc hiện thời. Thêm các
lời giải bộ phận này vào đồ thị tìm kiếm.

* Ví dụ: Xét bài toán điền các chữ số phân biệt thay cho các chữ cái S, E,

N, D, M, O, R, Y sao cho phép cộng sau là đúng:

SEND

Trí tuệ nhân tạo

MONEY

Các ràng buộc ban đầu:

Các chữ cái khác nhau không nhận cùng một giá trị.

Các ràng buộc số học (cộng có nhớ hoặc không có nhớ.

Giải

Gọi C1, C2, C3, C4 lần lượt lá số nhớ của các cột từ phải sang trái. Khi

đó ta xây dựng các ràng buộc cụ thể như sau:

E, N, D,O, R, Y thuộc tập {0 ..9}

(1)

S, M thuộc tập {1..9}

(2)

C1, C2, C3, C4 thuộc tập {0,1}

(3)

D + E = Y + 10*C1

(4)

N + R + C1 = E + 10*C2

(5)

E + O + C2 = N + 10*C3

(6)

S + M + C3 = O + 10*C4

(7)

M = C4

(8)

Từ ràng buộc (2) (3) và (8) suy ra M = 1 và C4=1 (9)

Từ ràng buộc (7) và (9) suy ra S +C3 = O + 9, lúc này có hai phương án

để lựa chọn:

Phương án 1:

C3 = 0, khi đó ta có S = O + 9, như vậy S = 9 và O = 0

(10-1)

Từ ràng buộc (6) ta có E + C2 = N, suy ra C2 = 1 và

E + 1 = N

(11-1)

Từ ràng buộc (5), ta có R + C1 = 9, như vậy R = 8 và C1 = 1 (12-1)

(do kết hợp với các ràng buộc (2) (3) và (10-1)).

∫

xlnxdx

∫

xdx

Trí tuệ nhân tạo

Từ ràng buộc (4) ta có D + E = Y +10. Đến bước này ta có thể khẳng

định các giá trị của D, E, Y chỉ có thể nhận trong tập {2, 3, 4, 5, 6, 7}. Ngoài ra
D + E >= 12. Vì vậy chỉ có các khả năng sau có thể xảy ra:

D = 5 và E = 7

D = 7 và E = 5 (hai truờng hợp này Y = 2)

D = 6 và E = 7

D = 7 và E = 6 (hai trường hợp sau Y = 3)

Xét khả năng thứ nhất. Từ ràng buộc (11-1) ta suy ra N = 8 mâu thuẫn

với (12-1) nên bị loại.

Xét khả năng thứ hai. Từ ràng buộc (11-1) ta suy ra N= 6. Kiểm tra điều

kiện bài toán đều thoả mãn. Vậy ta có nghiệm là:

S = 9, E = 5, N= 6, D = 7, M= 1, O = 0, R = 8, Y = 2.

Xét khả năng thứ ba. Từ ràng buộc (11-1) suy ra N = 8 mâu thuẫn với (12-1).

Xét khả năng thứ tư. Từ ràng buộc (11-1) suy ra N=7 = D mâu thuẫn.

Phương án 2:

C3 = 1. Từ ràng buộc (7) ta có S = O + 8, suy ra S = 8 và O = 0 (10-2)

(vì M=1 và S <= 9).

Từ ràng buộc (6) ta có E + C2 = N +10

C2=1 thì E= N+9 mâu thuẫn với ràng buộc (1) và (10-2).

C2=0 thì E=N+10 mâu thuẫn với ràng buộc (1).

Vậy phương án 2 không có lời giải.

∫

xlnxdx

∫

xdx

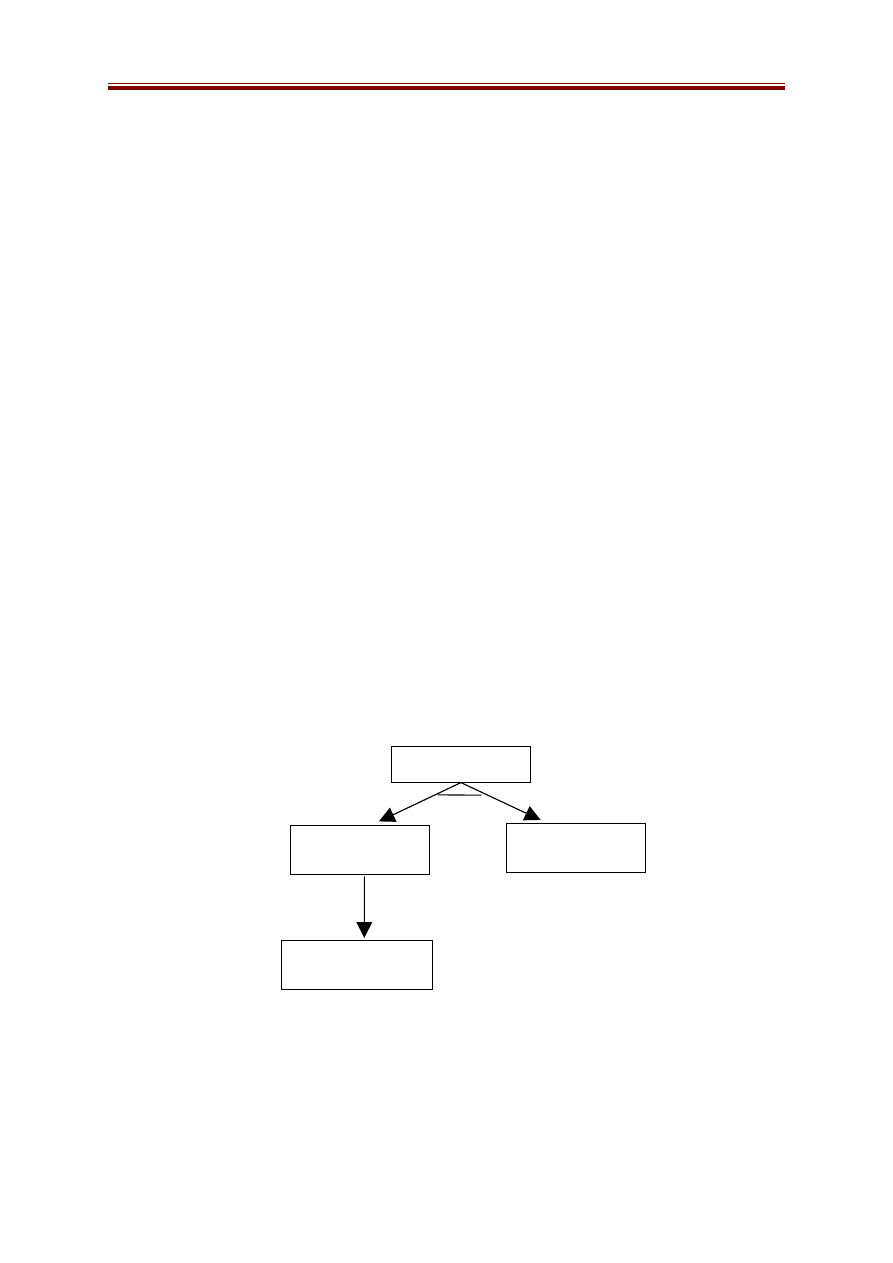
Trí tuệ nhân tạo

Chương 4

TÌM KIẾM LỜI GIẢI TRÊN ĐỒ THỊ VÀ/HOẶC

4.1. Đặt vấn đề

Trong chương 2, chúng ta đã nghiên cứu việc biểu diễn bài toán thông

qua các trạng thái và các toán tử. Khi đó việc tìm lời giải của bài toán được quy
về việc tìm đường đi trong không gian trạng thái. Trong chương này chúng ta sẽ
nghiên cứu một phương pháp luận khác để giải quyết vấn đề, dựa trên việc quy
vấn đề về các vấn đề con.

Ý tưởng chủ yếu là xuất phát từ bài toán ban đầu, tách ra các bài toán

con, quá trình này tiếp tục đối với các bài toán con cho đến khi gặp các bài toán
sơ cấp (bài toán có lời giải ngay).

Ví dụ 1: Xét bài toán tính tích phân

)

(ln

∫

Thông thường để tính tích phân bất định, chúng ta thường sử dụng các

quy tắc tính tích phân: tích phân của tổng, quy tắc tích phân từng phần hay các
phép biến đổi v.v… để đưa tích phân cần tính về tích phân của các hàm số sơ
cấp mà chúng ta đã biết cách tính. Đối với tích phân trên, áp dụng quy tắc tích
phân của tổng ta đưa về hai tích phân

∫

xlnxdx và tích phân

∫

dx. Áp dụng quy

tắc tích phân từng phần ta đưa tích phân

∫

xlnx về tích phân

∫

xdx. Quá trình trên

có thể biểu diễn bởi đồ thị trong Hình 4.1.

Hình 4.1

Trong bài toán tích phân, các tích phân cơ bản là các trạng thái kết thúc.

Ví dụ 2: Bài toán tìm đường đi trên bản đồ giao thông.

∫

x(lnx+x

)dx

∫

xlnxdx

∫

xdx

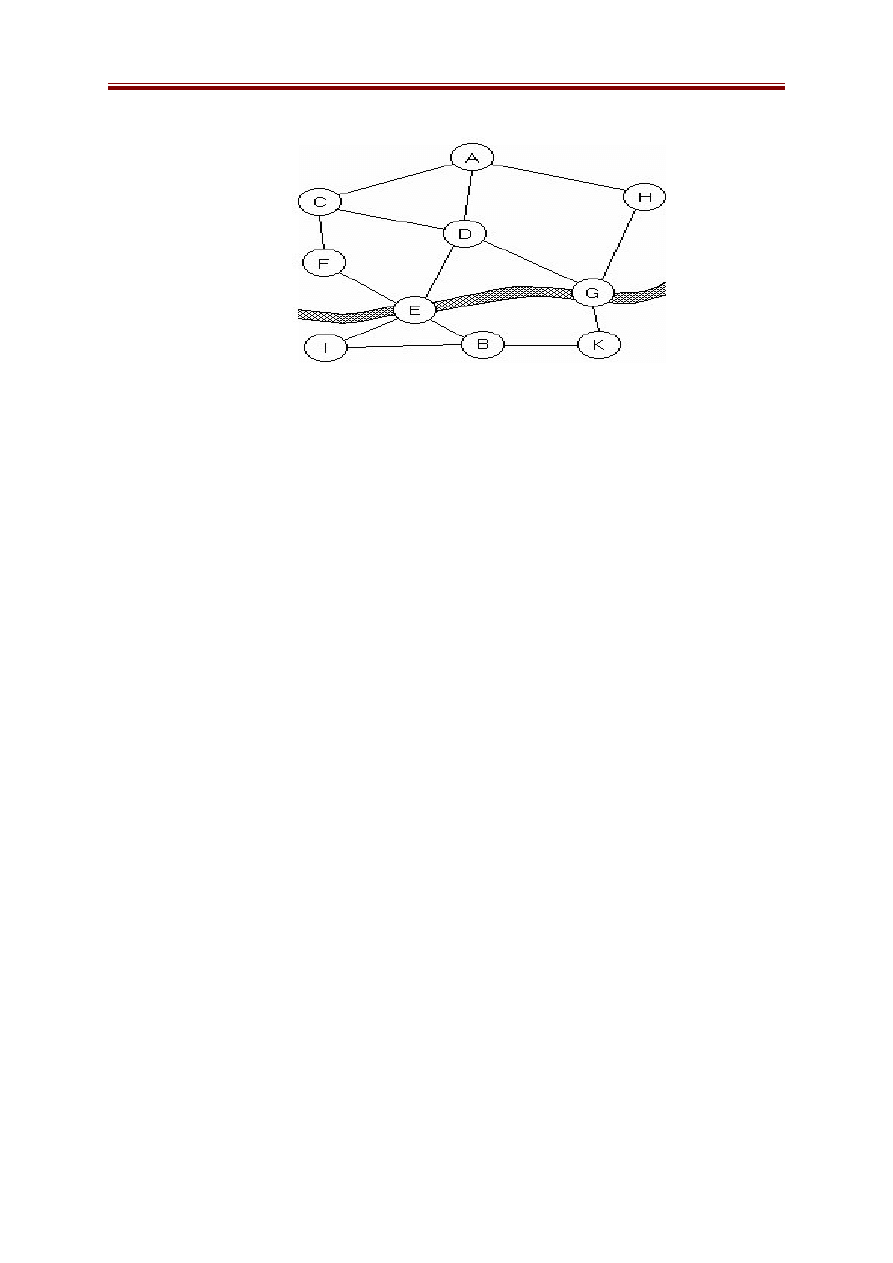
Trí tuệ nhân tạo

Bài toán này đã được phát biểu như bài toán tìm đường đi trong không

gian trạng thái, trong đó mỗi trạng thái ứng với một thành phố, mỗi toán tử ứng
với một con đường, nối thành phố này với thành phố khác. Bây giờ ta đưa ra
một cách biểu diễn khác dựa trên việc quy vấn đề về các vấn đề con..

Giả sử ta cần tìm đường đi từ thành phố A tới thành phố B. Có con sông

chảy qua hai thành phố E và G và có cầu qua sông ở mỗi thành phố đó. Mọi
đường đi từ A đến B chỉ có thể qua E hoặc G.

Như vậy bài toán tìm đường đi từ A đến B được quy về:

1) Bài toán tìm đường đi từ A đến B qua E (hoặc)

2) Bài toán tìm đường đi từ A đến B qua G.

Mỗi một trong hai bài toán trên lại có thể phân nhỏ như sau:

1) Bài toán tìm đường đi từ A đến B qua E được quy về:

1.1 Tìm đường đi từ A đến E (và)

1.2 Tìm đường đi từ E đến B.

2) Bài toán tìm đường đi từ A đến B qua G được quy về:

2.1 Tìm đường đi từ A đến G (và)

2.2 Tìm đường đi từ G đến B.

Quá trình rút gọn vấn đề như trên có thể biểu diễn dưới dạng đồ thị (đồ

thị và/hoặc) trong hình sau.

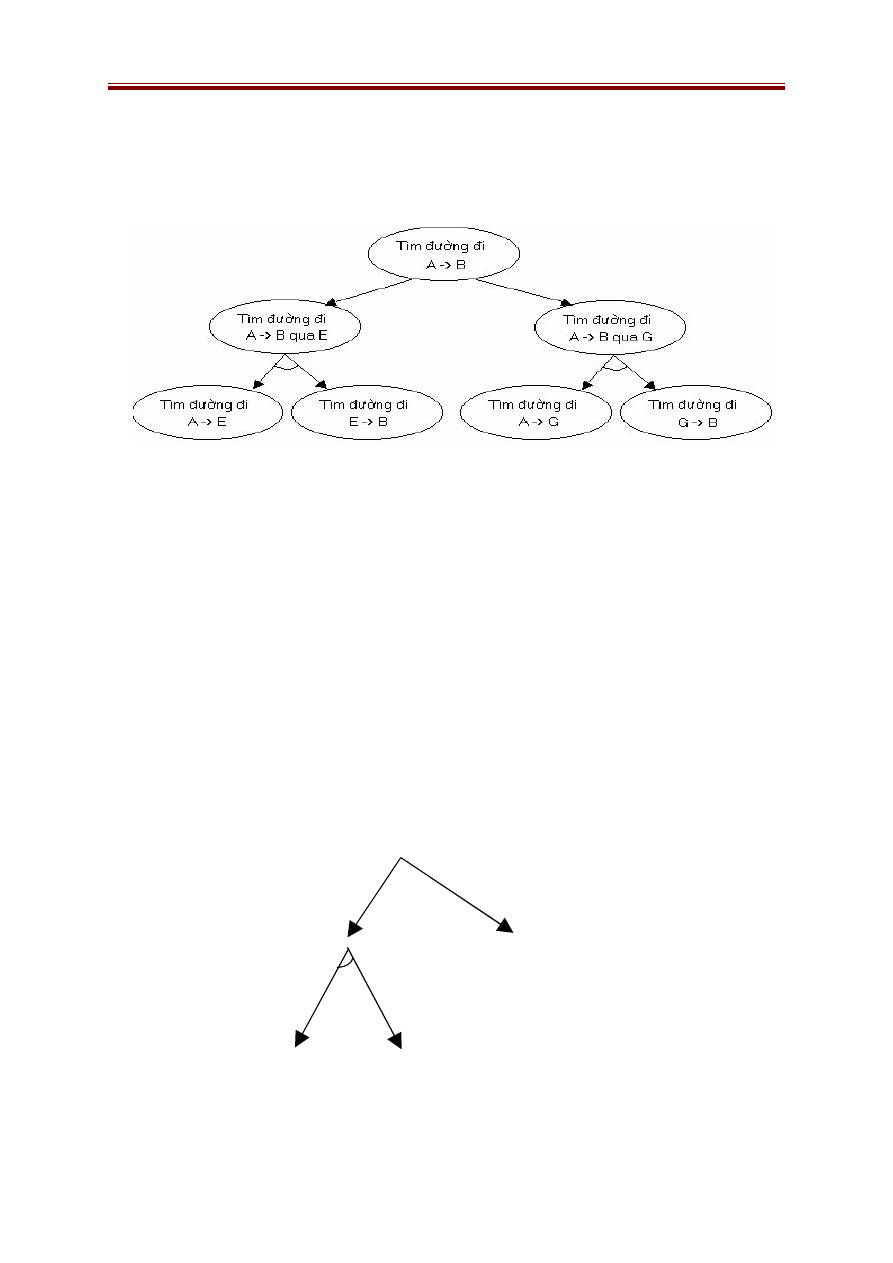
Trí tuệ nhân tạo

Ở đây mỗi bài toán tìm đường đi từ một thành phố tới một thành phố

khác ứng với một trạng thái. Các trạng thái kết thúc là các trạng thái ứng với các
bài toán tìm đường đi, chẳng hạn từ A đến C, hoặc từ D đến E, bởi vì đã có
đường nối A với C, nối D với E.

4.2. Đồ thị Và/Hoặc

Không gian trạng thái mô tả việc quy vấn đề về các vấn đề con có thể

biểu diễn dưới dạng đồ thị định hướng đặc biệt gọi là đồ thị và/hoặc. Đồ thị này
được xây dựng như sau:

Mỗi bài toán ứng với một đỉnh của đồ thị. Nếu có một toán tử quy bài

toán về các bài toán tương đương thì sẽ có các cung đi từ bài toán xuất phát đến
các bài toán tương đương đó. Nếu một toán tử quy bài toán về các bài toán con
thì cũng có các cung nối từ bài toán xuất phát đến các bài toán con, ngoài ra
giữa các cung này cũng có đường nối với nhau.. Chẳng hạn, giả sử bài toán A
được đưa về hai bài toán tương đương A1 và A2. Bài toán A1 lại được quy về
hai bài toán con B1 và B2, ta có biểu diễn như hình 4.2.

B2 Hình 4.2

Một cách hình thức ta có thể định nghĩa đồ thị và/hoặc như sau:

Trí tuệ nhân tạo

Đồ thị G = (V, E) được gọi là đồ thị VÀ/HOẶC nếu

∈

∀

, T(n) hoặc

các bài toán con của n (n gọi là các đỉnh VÀ) hoặc là tập các bài toán tương
đương với n (n gọi là đỉnh HOẶC).

Cách biểu diễn như sau:

...... n

n được gọi là đỉnh HOẶC (n

⇔

...

⇔

)

...... n

n được gọi là đỉnh VÀ (n

⇔

∩

...

∩

)

Khi đó để giải bài toán n ta phải tìm đồ thị con của G là một cây có gốc là

đỉnh xuất phát n sao cho mọi đỉnh trên đồ thị con này đưa về được các bài toán
sơ cấp (đỉnh kết thúc).

Nhận xét: Gọi

VA: tập các đỉnh VÀ

VO: tập các đỉnh HOẶC

•

Nếu VA=

∅

⇒

tìm lời giải trên đồ thị biểu diễn bằng không gian trạng thái

Khi đó:

- Bài toán n được gọi là giải được nếu:

+ hoặc n là đỉnh kết thúc

+ hoặc T(n)={n

, n

,..., n

} và nếu n là đỉnh HOẶC

)

...

(

∈

∃

⇒

sao cho

giải được, ngược lại n

giải được

...

∀

- Bài toán n được gọi là không giải được nếu:

+ hoặc n là đỉnh lá và n không phải là đỉnh kết thúc.

+ hoặc T(n)={n

, n

,..., n

}và nếu n là đỉnh HOẶC

)

...

(

∈

∃

⇒

sao cho n

không giải được, ngược lại n

không giải được

...

∀

•

Để tìm lời giải của bài toán khi được phân rã về đồ thị VÀ/HOẶC không
phải tìm đường đi mà phải đi tìm đồ thị con gọi là đồ thị con lời giải (hay
cây lời giải)

Trí tuệ nhân tạo

Cây lời giải là đồ thị con G’ của G thoả:

- Đỉnh gốc (xuất phát)

∈

∀

, n giải được.

•

Ta có sự tương quan:

Phân rã bài toán

Đồ thị Và/Hoặc

Bài toán

Đỉnh

Chuyển bài toán thành các bài toán con Cung

Bài toán sơ cấp

Đỉnh cuối

Các bài toán con phụ

Đỉnh VÀ

Các bài toán con độc lập

Đỉnh HOẶC

Giải bài toán

Tìm đồ thị con lời giải bài toán

4.3. Các phương pháp tìm kiếm lời giải trên đồ thị Và/Hoặc

Sau khi lựa chọn mô tả bài toán và các toán tử quy bài toán về bài toán

con, ta có thể xây dựng đồ thị Và/hoặc để giải quyết bài toán ban đầu hoặc
chứng tỏ tính không giải được của nó. Cũng như đồ thị trong không gian trạng
thái, đồ thị và/hoặc có thể cho dưới dạng tường minh hoặc không tường minh
trên cơ sở toán tử xây dựng.

Các phương pháp tìm kiếm trên đồ thị và/hoặc khác nhau chủ yếu ở

phương pháp lựa chọn và sắp xếp đỉnh trước khi tháo chúng. Tương tự như
trong không gian trạng thái, ta cung có các phương pháp sau:

Tìm kiếm theo chiều rộng.

Tìm kiếm theo chiều sâu.

Tìm kiếm cây lời giải có giá nhỏ nhất.

Các quá trình này khác hẳn với các quá trình lựa chọn trong không gian

trạng thái. Sự khác biệt chủ yếu là do việc kiểm tra tính kết thúc của quá trình

Trí tuệ nhân tạo

tìm kiếm và các phương pháp sắp xếp và lựa chọn đỉnh để xét phức tạp hơn
nhiều..

Thay cho việc tìm kiếm đỉnh thoả mãn điều kện đích, chúng ta phải tiến

hành tìm kiếm đồ thị lời giải. Do đó, ở những thời điểm nhất định, ta phải kiểm
tra xem đỉnh đầu có giải được hay không, nếu đỉnh đầu giải được thì kết thúc
công việc, trong trường hợp ngược lại thì tiếp tục xét các nút. Nếu đỉnh đang xét
không phải là đỉnh kết thúc và nó là đỉnh lá, tức là đỉnh không giải được. Lúc
này phải kiểm tra đỉnh đầu có phải không giải được hay không, nếu đúng thì
dừng, ngược lại, tiếp tục tìm kiếm.

Trước khi tìm kiếm lời giải trong đồ thị VÀ/HOẶC, chúng ta xây dựng

các hàm kiểm tra một đỉnh n nào đó tại thời điểm đang xét có giải được hay
không giải được không?

Function giaiduoc(n):boolean;

Begin

If <n so cap> then

giaiduoc:=true

else

if T(n)<>null then

if T(n)

⊂

then

)

(

))

(

giaiduoc

and

giaiduoc

∈

else

)

(

))

(

giaiduoc

∈

else

giaiduoc:=false;

End;

Function khonggd(n):boolean;

Trí tuệ nhân tạo

Begin

If T(n)<>null then

if T(n)

⊂

then

)

(

))

(

khonggd

∈

else

)

(

))

(

khonggd

and

khonggd

∈

else

if <T(n) khong so cap> then

khonggd:=true

else

khonggd:=false;

End;

* Ví dụ: Phương pháp tìm kiếm chiều rộng

Procedure TKR;

Begin

Push(n

, MO);

While MO<>null do

begin

n:=pop(MO);

push(DONG, n);

if T(n)<>null then

for

)

∈

Trí tuệ nhân tạo

begin

push(m, MO);

if T(m)=null then

if giaiduoc(m) then

if giaiduoc(n

) then

exit

else

for k

∈

MO do

if giaiduoc(k) then

MO:=MO-[k]

Else

If khonggd(m) then

If khonggd(n

) then

Exit

Else

For k

∈

MO do

if khonggd(k)

then

MO:=MO-[k]

end;

write(‘Khong ket luan’);

End;

* Nhận xét:

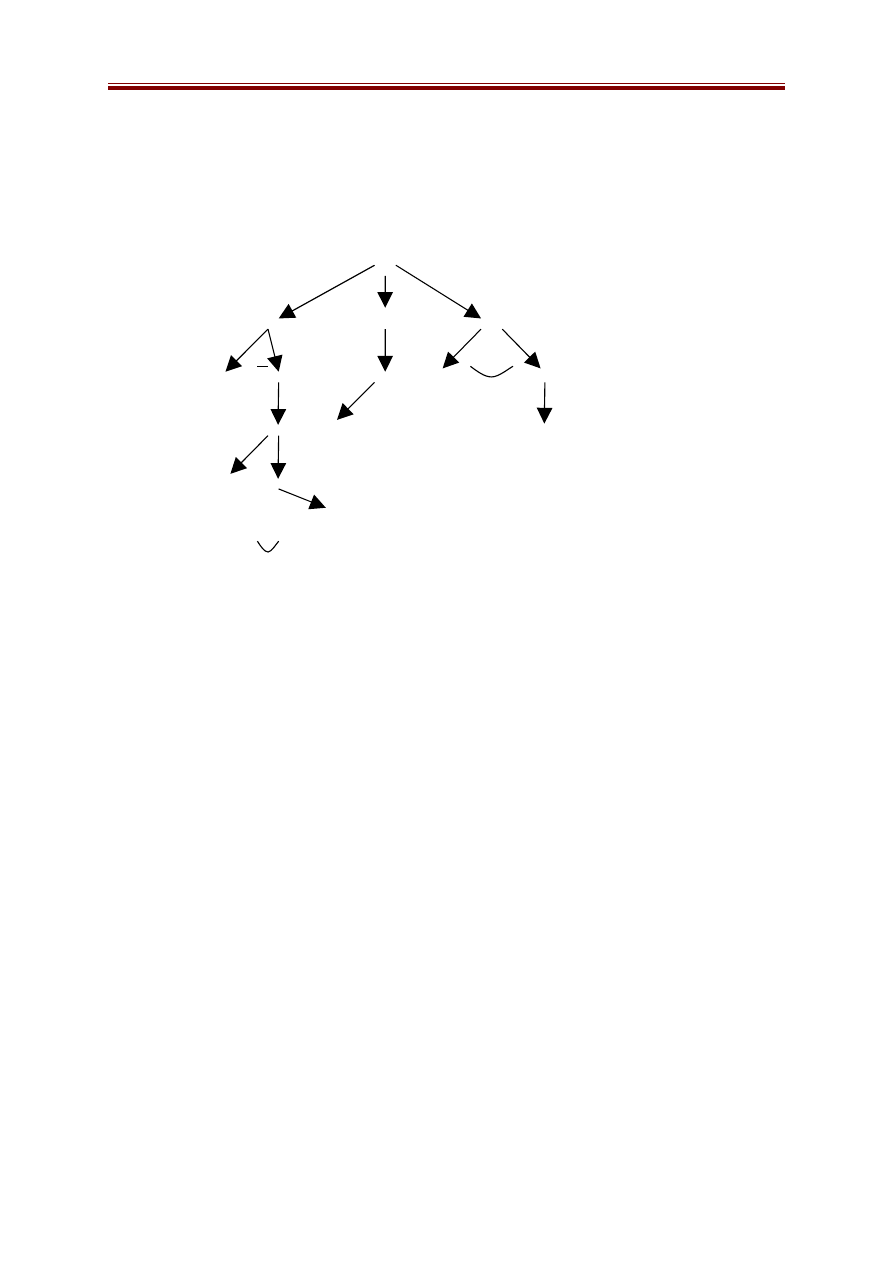
Trí tuệ nhân tạo

Nếu tồn tại cây lời giải thì thủ tục tìm kiếm rộng sẽ dừng và cho kết quả

là cây lời giải có độ cao nhỏ nhất.

Ví dụ.

Xét đồ thị Hình 4.3.

Hình 4.3

Các đỉnh kết thúc là các đỉnh đánh dấu *. Quá trình tìm kiếm lời giải của

đò thị trên bằng phương pháp tìm kiếm rộng có thể trình bày ở bảng sau

T(n)

DONG

B, C, D

B C D

, F

C D F

A B

D F G

A B C

, I

F G I

A B C D

G I J

A B C D F

I J

A B C D F G

Dừng

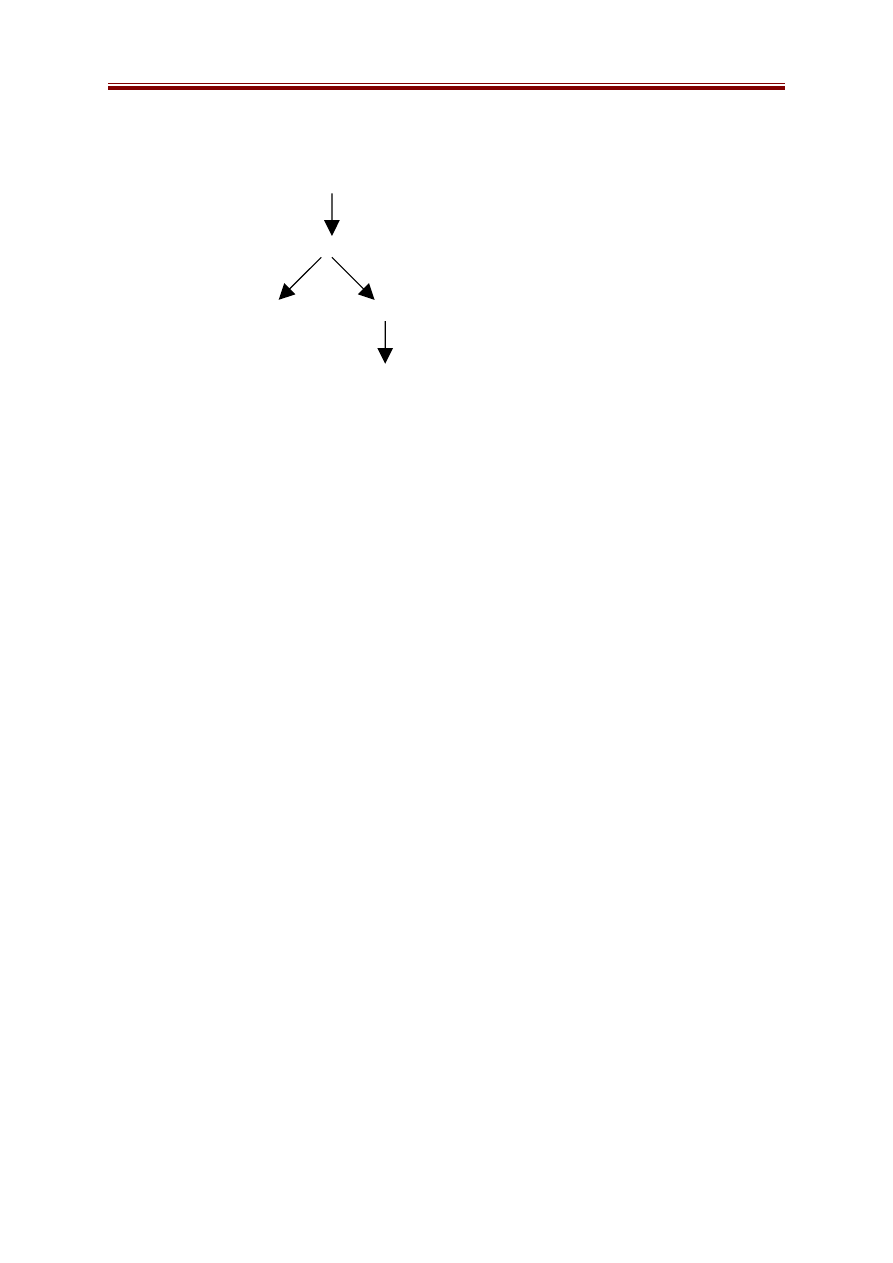
Trí tuệ nhân tạo

Cây lời giải ở hình sau:

(Xem thêm các ví dụ khác trong tài liệu tham khảo…)

Trí tuệ nhân tạo

Chương 5

BIỂU DIỄN BÀI TOÁN NHỜ LOGIC HÌNH THỨC

Trong chương này sẽ trình bày phương pháp biểu diễn vấn đề nhờ logic

hình thức và các phương pháp giải quyết vấn đề trên cách biểu diễn này.

Logic hình thức thường dùng để thu gọn quá trình tìm kiếm lời giải trước

khi giải quyết vấn đề, nhờ phân tích logic, có thể chứng tỏ rằng một bài toán
nào đó có thể giải được hay không?...

Ngoài ra, các kết luận logic rất cần ngay cả trong cách tiếp cận dựa trên

không gian trạng thái và quy bài toán về bài toán con. Chẳng hạn, trong các
phương pháp dựa trên không gian trạng thái, các kết luận logic dùng để kiểm tra
một trạng thái nào đó có phải là trạng thái đích hay không?...

Logic hình thức có thể được sử dụng để giải quyết những bài toán chứng

minh logic, chẳng hạn như chứng minh một khẳng định nào đó là đúng khi biết
những tiền đề ban đầu và các luật suy diễn. Đây là một dạng quen thuộc nhất và
được các chuyên gia TTNT quan tâm ngay từ đầu.

5.1. Logic mệnh đề

5.1.1. Mệnh đề

- Mệnh đề là một phát biểu có thể khẳng định tính đúng hoặc sai (hay giá

trị của nó chỉ có thể hoặc là đúng hoặc là sai).

- Các ký hiệu (symbol) của phép tính mệnh đề là các ký hiệu mệnh đề bởi

chữ cái latinh (biến mệnh đề) : a, b, c, p, q, P, Q, R …; các ký hiệu chân lý -
chân trị (truth symbol) : true -1, false -0 hay các phép toán kết nối (phép toán
logic) như : (phép tuyển (

∨

), phép hội (

∧

), phủ định (

, ~, ), phép kéo theo (

⇒

→

), phép tương đương (

⇔

≡

,=)).

Các ký hiệu mệnh đề biểu thị các mệnh đề (proposition) hay các phát biểu

về thế giới thực mà giá trị của chúng có thể là đúng hoặc sai.

Ví dụ:
Phát biểu: “Chiếc xe hơi kia màu đỏ”.
Phát biểu: "1+1=2" (có giá trị đúng).
Phát biểu: “Nước thì ướt”.

5.1.2. Câu

Câu trong phép tính mệnh đề được cấu tạo từ những ký hiệu sơ cấp theo

các luật sau đây :

Trí tuệ nhân tạo

- Tất cả các ký hiệu mệnh đề và ký hiệu chân lý đều là câu (sentences):

true, a, b và c là các câu.

- Phủ định của một câu là một câu : ¬ P và ¬ false là các câu
- Hội hay và của hai câu là một câu : P

∧

¬ P là một câu

- Tuyển hay hoặc của hai câu là một câu : P

∨

¬ P là một câu

- Kéo theo của một câu để có một câu khác là một câu : P

⇒

Q là một câu

- Tương đương của hai câu là một câu : P

∨

≡

R là một câu

Các câu hợp lệ được gọi là các công thức dạng chuẩn (well-formed

formula) hay WFF.

Trong các câu phép tính mệnh đề, các ký hiệu ( ) và [ ] dùng để nhóm các

ký hiệu vào các biểu thức con và nhờ đó kiểm soát được thứ tự của chúng trong
việc đánh giá biểu thức và diễn đạt.

Ví dụ: (P

∨

≡

R hoàn toàn khác với P

∨

≡

R).

5.1.3. Biểu thức

Một biểu thức là một câu hay công thức dạng chuẩn, của phép tính mệnh

đề khi và chỉ khi nó có thể được tạo từ những ký hiệu hợp lệ thông qua một dãy
những luật này.

Ví dụ: (( P

∨

⇒

≡

¬ P

∧

¬ Q

∧

R là một câu dạng chuẩn trong phép

tính mệnh đề vì : P, Q, R là các mệnh đề và do đó là các câu.

∧

Q, hội của hai câu là một câu.

∧

⇒

R, kéo theo của một câu là một câu.

¬ P và ¬ Q, phủ định của các câu là câu.
¬ P

∧

¬ Q, tuyển của hai câu là câu.

¬ P

∧

¬ Q

∧

R, tuyển của hai câu là câu.

(( P

∨

⇒

≡

¬ P

∧

¬ Q

∧

R , tương đương của hai câu là câu.

Đây là câu xuất phát, nó đã được xây dựng thông qua một loạt các luật

hợp lệ và do đó nó có dạng chuẩn.

Biểu thức logic dạng chuẩn: là biểu thức được xây dựng từ các biến mệnh

đề và các phép toán

∧

∨

Ví dụ: p

∧

(

∨

Thứ tự ưu tiên của các phép toán logic:

∧

∨

→

≡

5.1.4. Ngữ nghĩa của phép tính mệnh đề

Trí tuệ nhân tạo

Phép gán giá trị chân lý cho các mệnh đề phức tạp thường được mô tả

thông qua bảng chân trị như sau :

¬ P

∧

∨

⇒

≡

Ví dụ : Chân trị của mệnh đề (¬ P

∨

¬ Q)

≡

⇒

Q) được cho như trong

bảng sau :

¬ P

∨

¬ Q

⇒

(¬ P

∨

¬ Q)

≡

⇒

- Mọi biểu thức logic đều có thể chuyển về các biểu thức logic dạng

chuẩn.

- Hai biểu thức trong phép tính mệnh đề là tương đương nhau nếu chúng

có cùng giá trị trong mọi phép gán chân trị.

* Một số công thức biến đổi tương đương của các mệnh đề như sau:

5.2. Logic vị từ

5.2.1. Khái niệm

¬(¬P)

≡

∨

≡

(¬P

⇒

Luật tương phản: (P

⇒

≡

(¬Q

⇒

¬P)

Luật De Morgan: ¬(P

∨

≡

(¬P

∧

¬Q)

¬(P

∧

≡

(¬P

∨

¬Q)

Luật giao hoán: (P

∧

≡

∧

∨

≡

∨

Luật kết hợp: ((P

∧

≡

∧

R))

((P

∨

≡

∨

R))

Luật phân phối: P

∨

∧

≡

∨

∧

∨

∧

∨

≡

∧

∨

∧

Trí tuệ nhân tạo

Biểu diễn tri thức bằng mệnh đề gặp phải một trở ngại cơ bản là ta không

thể can thiệp vào cấu trúc của một mệnh đề. Hay nói một cách khác là mệnh đề
không có cấu trúc . Điều này làm hạn chế rất nhiều thao tác suy luận .

Do đó, người ta đã đưa vào khái niệm vị từ và lượng từ (

∀

: với mọi,

∃

tồn tại) để tăng cường tính cấu trúc của một mệnh đề.

- Trong logic vị từ, một mệnh đề được cấu tạo bởi hai thành phần là các

đối tượng tri thức và mối liên hệ giữa chúng (gọi là vị từ). Các mệnh đề sẽ
được biểu diễn dưới dạng:

Vị từ (<đối tượng 1>, <đối tượng 2>, …, <đối tượng n>)

Ví dụ: Để biểu diễn vị của các trái cây, các mệnh đề sẽ được viết lại

thành :

Cam có vị Ngọt

⇒

Vị (Cam, Ngọt)

Cam có màu Xanh

⇒

Màu (Cam, Xanh)

Kiểu biểu diễn này có hình thức tương tự như hàm trong các ngôn ngữ

lập trình, các đối tượng tri thức chính là các tham số của hàm, giá trị mệnh đề
chính là kết quả của hàm (thuộc kiểu BOOLEAN).

- Với vị từ, ta có thể biểu diễn các tri thức dưới dạng các mệnh đề tổng

quát, là những mệnh đề mà giá trị của nó được xác định thông qua các đối tượng
tri thức cấu tạo nên nó.

Ví dụ:

Chẳng hạn tri thức : "A là bố của B nếu B là anh hoặc em của một người

con của A" có thể được biểu diễn dưới dạng vị từ như sau :

Bố (A, B) = Tồn tại Z sao cho : Bố (A, Z) và (Anh(Z, B) hoặc Anh(B,Z))

Trong trường hợp này, mệnh đề Bố(A,B) là một mệnh đề tổng quát

Như vậy nếu ta có các mệnh đề cơ sở là :

a) Bố ("An", "Bình") có giá trị đúng (Anh là bố của Bình)

b) Anh("Tú", "Bình") có giá trị đúng (Tú là anh của Bình)

Trí tuệ nhân tạo

thì mệnh đề c) Bố ("An", "Tú") sẽ có giá trị là đúng. (An là bố của Tú).

5.2.2. Cú pháp vị từ

+ Ký hiệu vị từ: là tập hợp gồm các chữ cái, chữ số, ký hiệu “_”, và được

bắt đầu bằng chữ cái. Ký hiệu vị từ có thể là:

- Hằng: chỉ một đối tượng, thuộc tính được biểu diễn bằng chuỗi ký tự

bắt đầu bằng chữ cái thường hoặc các chữ số hoặc chuỗi ký tự đặt trong bao
nháy. Ví dụ: a,b, c, blue, rain, “An”, “Ba”,...

- Biến: chỉ một lớp tổng quát các đối tượng, thuộc tính, tên biến luôn bắt

đầu bằng chữ cái viết hoa. Ví dụ: X, Y, Z, U, V, Students, People...

- Vị từ: được biểu diễn bằng chuỗi ký tự bắt đầu bằng chữ cái thường. Ví

dụ: p, q, r, s, like,...

Mỗi vị từ là vị từ của n biến (n

≥

0). Các ký hiệu vị từ không có biến là

các ký hiệu mệnh đề.

Ví dụ:

like(X,Y) là vị từ của hai biến
u(X) là vị từ một biến
r là vị từ không biến

- Hàm: f, g, cos, sin, mother,...
Mỗi hàm là hàm của n biến (n

≥

1). Ví dụ: cos, sin là hàm một biến.

+ Biểu thức hàm: là một ký hiệu hàm theo sau bởi n đối số.
Ví dụ: father(david), price(bananas), like(tom, football).
+ Mục hay hạng thức (term): là một hằng, một biến hay một biểu thức

hàm.

+ Câu sơ cấp: là một hằng vị từ với n ngôi theo sau bởi n thành phần

nằm trong cặp dấu ( ), cách nhau bởi dấu ‘,’, và kết thúc với dấu ‘.’

- Trị chân lý true, false là các câu sơ cấp.
- Câu sơ cấp còn được gọi là: biểu thức nguyên tử, nguyên tử hay mệnh

đề

Ví dụ : friends(helen, marry). likes(hellen, mary).

likes(helen, sister(mary)). likes(X, ice-cream).

Ký hiệu vị từ trong các câu này là friends, likes.
+ Câu (hay công thức): được tạo ra bằng cách kết hợp các câu sơ cấp sử

dụng:

Trí tuệ nhân tạo

- Các phép kết nối logic: :

∧

(hội),

∨

(tuyển),

(phủ định),

⇒

(kéo theo),

⇔

hay

≡

(kéo theo nhau, tương đương).

- Các lượng tử biến:

o Lượng tử phổ biến:

∀

(với mọi): dùng để chỉ một câu là đúng với

mọi giá trị của biến lượng giá
Ví dụ:

∀

X, p(X) nghĩa là với mọi giá trị của biến X đều làm cho biểu

thức p đúng.

∀

X likes(X, ice-cream)

o Lượng tử tồn tại:

∃

(tồn tại): dùng để chỉ một câu là đúng với một

số giá trị nào đó của biến lượng giá.
Ví dụ:

∃

Y, p(Y) nghĩa là có ít nhất một giá trị của biến Y để làm cho

biểu thức p đúng.

∃

Y friends(Y,tom).

Ví dụ về câu:
likes(helen, chocolat)

∧

¬ likes(bart, chocolat).

∃

X foo(X,two,plus(two,three))

∧

equal(plus(three,two),five).

(foo(two, two,plus(two,three)))

⇒

(equal(plus(three,two),five)= true.

+ Các ký hiệu ngăn cách: dấu phẩy, dấu mở ngoặc và dấu đóng ngoặc.

5.2.3. Ngữ nghĩa phép tính vị từ

Tương tự như phép tính mệnh đề, ngữ nghĩa của phép tính vị từ cung cấp

một cơ sở để xác định chân trị của các biểu thức dạng chuẩn. Chân trị của các
biểu thức phụ thuộc vào ánh xạ từ các hằng, các biến, các vị từ và các hàm vào
các đối tượng và quan hệ trong lĩnh vực được đề cập.

Sự thông dịch (cách diễn giải) của một tập hợp các câu phép tính vị từ: là

một sự gán các thực thể trong miền của vấn đề đang đề cập cho mỗi ký hiệu
hằng, biến, vị từ và hàm.

Giá trị chân lý của một câu sơ cấp được xác định qua sự thông dịch. Đối

với các câu không nguyên tử, sử dụng bảng chân lý cho cho các phép nối kết,
và:

- Giá trị của câu

∀

X <câu> là true nếu <câu> là T cho tất cả các phép

gán có thể được cho X.
- Giá trị của câu

∃

X <câu> là true nếu tồn tại một phép gán cho X làm

cho <câu> có giá trị T.

Trí tuệ nhân tạo

Ví dụ 1: Câu student(“Lan”)

∧

student(“An”) nhận giá trị true nếu cả hai

câu student(Lan) và student(An) đều có giá trị true, tức là cả Lan và An
đều là sinh viên.
Ví dụ 2:
Ngữ nghĩa của các câu

∀

x (G), trong đó G là một công thức nào đó được

xác định là ngữ nghĩa của công thức là hội của tất cả các công thức nhận được
từ công thức G bằng cách thay X bởi một đối tượng trong miền đối tượng.
Chẳng hạn, nếu miền đối tượng gồm ba người {Lan, An, Hoa} thì ngữ nghĩa
của câu

∀

x, student(x) được xác định là ngữ nghĩa của câu student(“Lan”)

∧

student(“An”)

∧

student(“Hoa”). Câu này đúng khi và chỉ khi cả ba câu thành

phần đều đúng, tức là cả Lan, Hoa, An đều là sinh viên. Như vậy, công thức

∀

(G) là đúng nếu và chỉ nếu mọi công thức nhận được từ G bằng cách thay X bởi
một đối tượng bất kỳ trong miền đối tượng đều đúng, tức là G đúng cho tất cả
đối tượng X trong miền đối tượng.

Ngữ nghĩa của công thức

∃

x (G) được xác định như là ngữ nghĩa của

công thức là tuyển của tất cả các công thức nhận được từ công thức G bằng
cách thay X bởi một đối tượng trong miền đối tượng. Chẳng hạn, nếu ngữ nghĩa
của câu younger(X, 20) là “X trẻ hơn 20 tuổi” và miền đối tượng gồm ba người
{Lan, Hoa, An} thì ngữ nghĩa của câu

∃

X younger(x, 20) là ngữ nghĩa của câu

younger(“Lan”, 20)

∨

younger(“Hoa”, 20)

∨

younger(“An”, 20). Câu này nhận

giá trị True nếu và chỉ nếu ít nhất một trong ba người Lan, Hoa, An trẻ hơn 20
tuổi. Như vậy, công thức

∃

x(G) là đúng nếu và chỉ nếu một trong các công thức

nhận được từ G bằng cách thay X bởi một đối tượng trong miền đối tượng là
đúng.

Ví dụ 3: Cho trước một tập hợp các quan hệ gia đình như sau:
mother (eve,abel) mother(eve,cain)
father(adam,abel) father(adam,cain)

∀

Y father(X,Y)

∨

mother(X,Y)

⇒

parent(X,Y)

∀

∃

Z parent(Z,X)

∧

parent(Z,Y)

⇒

sibling(X,Y)

Ta có thể suy luận:
parent(eve,abel)

parent(eve,cain)

parent(adam,abel) parent(adam,cain)
sibling(abel,cain) sibling(cain,abel)
sibling(abel,abel) sibling(cain,cain)

! Không có nghĩa

Trí tuệ nhân tạo

Chúng ta có các tương đương sau đây:

∀

x (G(x))

≡

∀

y (G(y))

∃

x (G(x))

≡

∃

y (G(y))

(

∀

x (G(x)))

≡

∃

x (

G(x))

∃

x (G(x))

≡

∀

x (

G(x))

∀

x (G(x)

∧

H(x))

≡

∀

x (G(x))

∧

∀

x (H(x))

∃

x (G(x)

∨

H(x))

≡

∃

x (G(x))

∨

∃

x (H(x))

5.2.4. Phép tính vị từ bậc nhất

Phép tính vị từ bậc nhất cho phép các biến lượng giá tham chiếu đến các

đối tượng trong miền của vấn đề đang đề cập nhưng không được tham chiếu đến
các vị từ và hàm.

Ví dụ 2.8 :
- Ví dụ không hợp lệ:

∀

(Likes) Likes(helen, ice-cream)

- Ví dụ hợp lệ:
Nếu ngày mai trời không mưa, Tom sẽ đi biển.
¬weather(rain, tomorrow)

⇒

go(tom, sea)

Tất cả các cầu thủ bóng rổ đều cao.

∀

X ( basketball_player(X)

⇒

tall(X) )

Có người thích coca-cola.

∃

X person(X)

∧

likes(X, coca-cola)

Không ai thích thuế.
¬

∃

X likes(X, taxes)

Hầu hết bất kỳ câu đúng ngữ pháp nào cũng có thể biểu diễn trong phép

tính vị từ bậc nhất bằng cách sử dụng các ký hiệu, các phép kết nối và ký hiệu
biến.

5.3. Các luật suy diễn

Ngữ nghĩa của phép tính vị từ cung cấp một cơ sở cho lý thuyết hình thức

về suy diễn logic. Khả năng suy ra những biểu thức đúng mới từ một tập hợp
các khẳng định đúng là một đặc trưng quan trọng của phép tính vị từ. Logic vị
từ dùng các luật suy diễn sau :

Luật Modus Ponens (MP):

P
P

⇒

Trí tuệ nhân tạo

Ví dụ: Nếu ta có quan sát sau đây “nếu trời mưa thì sân ướt” (P

⇒

Q) và

“trời đang mưa” (P) thì ta dễ dàng suy ra được “sân ướt” (Q).

Luật Modus Tollens (MT):

⇒

¬ P

Luật triển khai phổ biến (Universal Instantiation -UI):

∀

X P(X)

a thuộc miền xác định của X
P(a)

Ví dụ: “Tất cả mọi người đều chết và Socrates là người do đó Socrates sẽ chết”

Cho trước:
(1)

∀

X (man(X)

⇒

mortal(X))

(2) man(socrates)
=>
(3) man(socrates)

⇒

mortal(socrates) từ (1),(2) bằng luật UI.

(4) mortal(socrates)

từ (3) và (2) bằng luật MP.

5.4. Đối sánh mẫu và phép hợp nhất

5.4.1. Giải thuật đối sánh mẫu

(1) Hằng / hằng đối sánh : chỉ khi chúng giống hệt nhau
VD: tom không đối sánh với jerry
(2) Hằng a / biến X đối sánh:

a. Biến chưa kết buộc: biến trở thành kết buộc với hằng => Khi đó ta
có phép thế {a/X}
b. Biến đã kết buộc : xem (1)

(3) Biến X/ biến Y đối sánh:

a. Hai biến chưa kết buộc: luôn luôn đối sánh => Khi đó ta có phép thế
{X/Y}
b. Một biến kết buộc và một biến chưa kết buộc: xem (2)
c. Hai biến kết buộc: xem (1)

(4) Biểu thức / biểu thức đối sánh: chỉ khi các tên hàm hoặc vị từ, số

ngôi giống nhau thì áp dụng đối sánh từng đối số một.

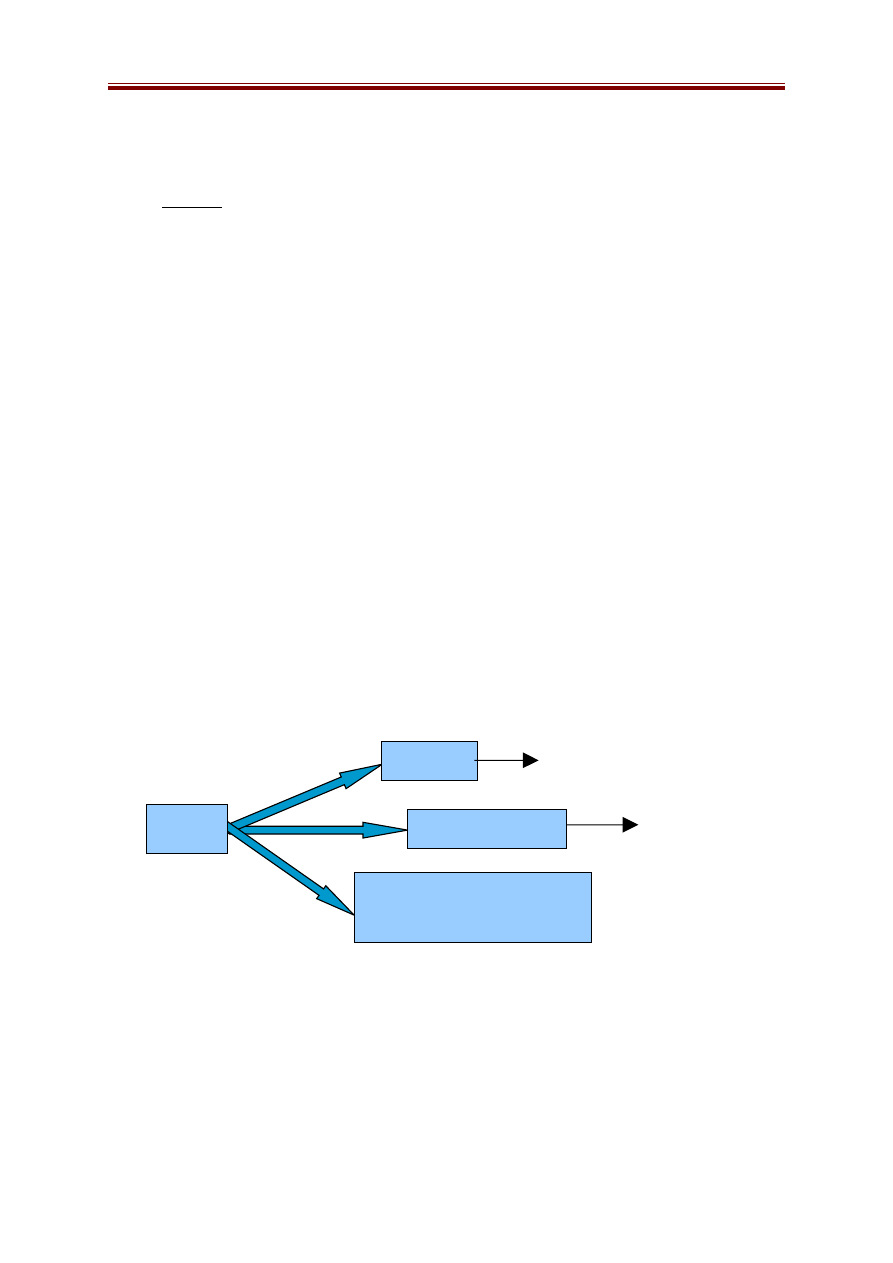
Trí tuệ nhân tạo

VD: goo(X)

- không đối sánh với foo(X) hay goo(X,Y)
- đối sánh với goo(foo(Y)) với phép thế {foo(Y) / X}

Lưu ý : Phạm vi của một biến là một câu. Một khi biến đã bị kết buộc,

các phép hợp nhất theo sau và các suy luận kế tiếp phải giữ sự kết buộc này.

VD: man(X) => mortal(X)

Nếu ta thế X bởi socrates thì ta được:

man(socrates) => mortal(socrates)

5.4.2. Phép hợp nhất

Phép hợp nhất (unification) là một thuật toán dùng để xác định những

phép thế cần thiết để làm cho hai biểu thức vị từ đối sánh (match) nhau.

Để áp dụng các luật như MP, một hệ suy diễn phải có khả năng xác định

khi nào thì hai biểu thức là một hay còn gọi là đối sánh (match).

Hợp nhất và các luật suy diễn khác như Modus ponens cho phép chúng ta

tạo ra các suy diễn dựa trên một tập hợp các khẳng định logic. Phép hợp nhất
phức tạp do có thể thay thế một biến với bất kỳ mục nào gồm cả những biến và
những biểu thức hàm khác với độ phức tạp tùy ý. Những biểu thức này tự thân
chúng lại có thể chứa các biến.

Một biến có thể thay thế bởi một mục bất kỳ:

Ví dụ: Đối sánh foo(X,a,goo(Y)) với:

Biến

Hằng

Biểu thức hàm có thể
chứa các biến khác

Biến khác

Thay thế bởi

Biến đã kết buộc
(bound)

Biến chưa kết buộc
(unbound)

Trí tuệ nhân tạo

foo(X,b,foo(Y))

không đối sánh

foo(X,Y)

không đối sánh

moo(X,a,goo(Y))

không đối sánh

foo(fred,a, goo(Z))

{fred/X, Z/Y}

foo(W,a,goo(jack))

{W/X,jack/Y}

foo(Z,a,goo(moo(Z)))

{Z/X,moo(Z)/Y}

Nói chung một quá trình giải quyết vấn đề sẽ đòi hỏi nhiều suy diễn và do

đó cần nhiều phép hợp nhất nói tiếp nhau. Các chương trình giải quyết vấn đề
logic phải duy trì tính nhất quán của các phép thế biến. Điều này được phát biểu
trong giải thuật đối sánh mẫu.

(Xem thêm trong tài liệu tham khảo…)

5.5. Một số giải thuật chứng minh

Một trong những vấn đề khá quan trọng của logic mệnh đề là chứng minh

tính đúng đắn của phép suy diễn (a

⇒

b). Đây cũng chính là bài toán chứng minh

thường gặp trong toán học.

Rõ ràng rằng với hai phép suy luận cơ bản của logic mệnh đề (Modus

Ponens, Modus Tollens) cộng với các phép biến đổi hình thức, ta cũng có thể
chứng minh được phép suy diễn. Tuy nhiên, thao tác biến đối hình thức là rất
khó cài đặt được trên máy tính. Thậm chí điều này còn khó khăn với cả con
người!

Với công cụ máy tính, bạn có thể cho rằng ta sẽ dễ dàng chứng minh

được mọi bài toán bằng một phương pháp "thô bạo" là lập bảng chân trị . Tuy
về lý thuyết, phương pháp lập bảng chân trị luôn cho được kết quả cuối cùng
nhưng độ phức tạp của phương pháp này là quá lớn, O(2

) với n là số biến mệnh

đề.

Sau đây chúng ta sẽ nghiên cứu các phương pháp chứng minh mệnh

đề (hoặc vị từ) với độ phức tạp chỉ có O(n ):

5.5.1. Bài toán

Cho tập các giả thiết dưới dạng các biểu thức logic mệnh đề (hoặc vị từ)

GT={GT

, GT

, ...GT

}. Hãy chứng minh tập kết luận KL={KL

, KL

,..., KL

5.5.2. Thủ tục Wong. H (Vương Hạo)

Vào: Cho các biểu thức mệnh đề giả thiết GT

, GT

, ...,GT

Trí tuệ nhân tạo

Các biểu thức mệnh đề kết luận KL

, KL

,...,KL

Ra: Chứng minh GT

, GT

,...,GT

→

, KL

,...,KL

: True

(Thông báo “thành công” nếu GT

∧

...

∧

→

...KL

)

* Phương pháp:

{ for i=1 to n do

{ Trans (GT

); //đưa từng GT về dạng chuẩn

VT {GT

}

∪

VT; } //đưa vào vế trái

for i=1 to m do

{ Trans (KL

); //đưa từng GT về dạng chuẩn

VP {KL

}

∪

VP; } //đưa vào vế phải

P {(VT, VP)}; //P: tập chứa các bài toán (VT, VP)
While P ≠

{ (VT, VP) get (P); //Lấy bài toán trong P
if VT

∩

VP =

then

{ chuyen (VT, VP);
if VT

∩

VP =

then

if not tach (VT, VP) then

Exit (“ko thành công”);

}

} P : các bài toán con qua phép tach (VT, VP) mà có

write (“thành công”);
}

* Chú ý:
- Trans (BT:) là thủ tục đưa biểu thức BT về biểu thức chỉ chứa các phép toán

∧

∨

dưới dạng chuẩn (ví như chuẩn hội: hội các tuyển, chuẩn tuyển: tuyển các

hội).

Chú ý: a

⇒

b =

∨

∧

b) =

∨

Ví dụ: Biểu thức

⇒

∨

∧

d) có thể đưa về thành:

1. (a

∧¬

∨

∧

2. (a

∨

∧

∨

∧

(

∨

∧

(

∨

- chuyen (VT, VP): thủ tục chuyển các GT

, KL

ở dạng phủ định.

Ví dụ:

∨

∧

s),

g, p

∨

⇒

Trí tuệ nhân tạo

→

∨

q, p

∨

r, p

⇒

∧

s), g, s

Và nếu GT

có phép

∧

thì thay thế phép

∧

bằng dấu "," . Nếu KL

có phép

∨

thì thay thế phép

∨

bằng dấu ",".

Ví dụ:

∧

q, r

∧

(

∨

⇒

→

p, q, r,

∨

⇒

- tach (VT, VP): thủ tục tách (VT, VP) thành 2 danh sách con nếu GT

có

phép

∨

hoặc ở KL

có phép

∧

. Nếu tách được thì thủ tục tach (VT,VP) nhận giá trị

True.

Ví dụ :

∨

⇒

q tách thành 2 dòng:

⇒

q p, q

⇒

- Một dòng được chứng minh nếu tồn tại chung một mệnh đề ở ở cả hai

phía.

Ví dụ :

p, q

⇒

q được chứng minh

⇒

→

⇒

p, q

- Nếu một dòng không còn phép nối

∧

hoặc

∨

ở cả hai vế và ở 2 vế không

có chung một biến mệnh đề thì dòng đó không được chứng minh.

- Một vấn đề được chứng minh nếu tất cả dòng dẫn xuất từ dạng chuẩn

ban đầu đều được chứng minh.

* Các ví dụ:

VD1: Cần chứng minh rằng từ a

∧

→

c và b

∧

→

d và a và b, suy ra d

Giải:

Viết lại dưới dạng chuẩn:

Trí tuệ nhân tạo

(

∨

∧

(

∨

∧

→

∨

c ,

∨

d, a , b

→

- Áp dụng thủ tục tách (VT,VP) ta có 2 dòng:

∨

d, a , b, VP = d

∨

c ,

∨

d, a , b, VP = d

- Như vậy: P = {(VT

, VP), (VT

, VP)}

Áp dụng thủ tục chuyển (VT

,VP) đưa về dạng

∨

d, a , b, VP = d, a

Lúc này VT

∩

VP ≠

tức là VT

→

- Cứ tiếp tục như vậy để xử lý (VT2, VP) ta có kết quả bài toán được

chứng minh (Xem hình sau).

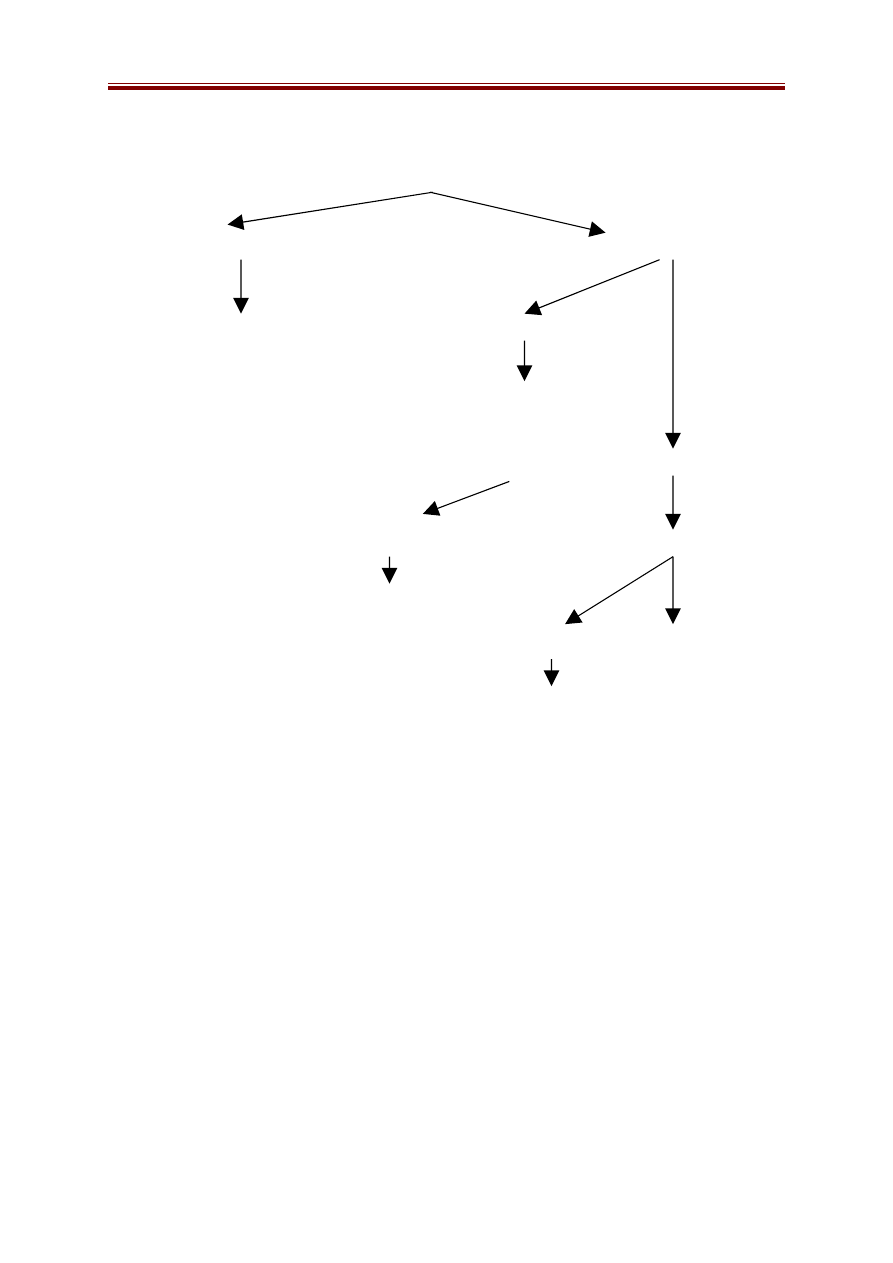
Trí tuệ nhân tạo

∨

c ,

∨

d, a , b

→

a ,

∨

d, a , b

→

∨

d, a , b

→

∨

d, a , b

→

d, a : CM

∨

d, a , b

→

∨

d, a , b

→

d, b : CM

∨

d, a , b

→

b, a , b

→

d c,

∨

d, a , b

→

c, a , b

→

d , b : CM

c, a , b

→

d c, d, a , b

→

d: CM

c, a , b

→

d, c : CM

VD2: Xét các câu đúng sau:

Trí tuệ nhân tạo

“Nếu trời mưa thì Lan mang theo dù”
“Nếu Lan mang theo dù thì Lan không bị ướt”
“Nếu trời không mưa thì Lan không bị ướt”
a. Xây dựng các câu trên bằng các biểu thức logic mệnh đề
b. Hãy chứng minh rằng “Lan không bị ướt” bằng phương pháp Vương

Hạo
Giải

a. r: “Trời mưa”
u: “Lan mang theo dù”
w: “Lan bị ướt”
Lúc đó, ta có các biểu thức logic đúng sau:
r

→

b.Ta phải chứng minh (r

→

∧

→

∧

(

→

w: True

5.5.3. Thủ tục Robinson 1 (dùng cho logic mệnh đề)

Thuật giải này do Robinson đề xuất và hoạt động dựa trên phương pháp

chứng minh phản chứng.

Để chứng minh rằng từ các GT={GT

, GT

, ...GT

} suy ra một trong các

kết luận KL={KL

, KL

,..., KL

}, ta chỉ cần lấy phủ định của KL

, KL

,..., KL

hợp cùng giả thiết. Nếu suy ra được mâu thuẫn thì quá trình chứng minh xong.
Vào: Cho các biểu thức mệnh đề giả thiết GT

, GT

, ...,GT

Các biểu thức mệnh đề kết luận KL

, KL

,...,KL

Ra: (Thông báo “thành công” nếu GT

∧

...

∧

→

∨

...

∨

)

* Phương pháp:

{ for i=1 to n do

{ Trans (GT

);

P {GT

}; }

for i=1 to m do

{ Trans (KL

);

P {

}; }

Trí tuệ nhân tạo

if mt(P) then Exit (“thành công”); //nếu mâu thuẫn P
P

: =

;

While P ≠ P

and

mt(P) do

: = P;

hopgiai(P); }
if mt(P) then Exit (“thành công”);
else Exit (“ko thành công”);

}

* Chú ý:
- Mâu thuẫn: Nếu trong P mà có 2 mệnh đề:

hoặc

= p

( với p

≠ p

)

thì trong P có mâu thuẫn.

- Hợp giải: Nếu trong P mà có 2 mệnh đề:

∨

= a

∨

thì ta bổ sung vào P thêm mệnh đề mới: p

= b

∨

* Ví dụ:

Cần chứng minh rằng từ a

∧

→

c và b

∧

→

d và a và b, suy ra d

tức {a

∧

→

c, b

∧

→

d, a, b}

→

{d}

Giải:

P = {

∨

c ,

∨

d, a , b,

Để đơn giản ta viết như sau:

∨

3. a

4. b

Trí tuệ nhân tạo

Quá trình hợp giải như sau:

∨

c (là kết quả hợp giải dòng 1 và dòng 3, ký hiệu là Res(1A,3), chữ

A chỉ ra rằng lấy thành phần đầu tiên trong trong 1).

∨

Res(1B,4)

∨

Res(2A,4)

∨

Res(2C,5)

10. c

Res(3,7A)

11.

Res(4,9A)

12. Mâu thuẫn giữa 10 và 11

Chứng minh xong.

(Xem hình sau)

∨

c a

∨

Mâu thuẫn

5.5.4. Thủ tục Robinson 2 (dùng cho logic vị từ)

(Xem thêm trong tài liệu tham khảo…)

Trí tuệ nhân tạo

Chương 6

BIỂU DIỄN TRI THỨC VÀ CÁC PHƯƠNG PHÁP SUY DIỄN

Như ta đã biết con người sống trong môi trường có thể nhận được thế giới

nhờ các giác quan và sử dụng tri thức tích luỹ được và nhờ khả năng lập luận,
suy diễn, con người có thể đưa ra các hành động hợp lý cho công việc mà con
người đang làm.

Trong khi đó mục tiêu của trí tuệ nhân tạo ứng dụng là thiết kế các tác

nhân thông minh (intelligent agent) cũng có khả năng đó như con người. Tác
nhân thông minh là bất cứ cái gì có thể nhận thức được môi trường thông qua
các bộ cảm nhận (sensors) và đưa ra hành động hợp lý đáp ứng lại môi trường
thông qua bộ phận hành động (effectors). Ví dụ: robots, softrobot (software
robot), các hệ chuyên gia,...là các tác nhân thông minh.

Chính vì vậy, muốn xây dựng một trí thông minh nhân tạo, ta cần phải có

các phương pháp đưa tri thức vào máy tính được gọi là biểu diễn tri thức.

Tri thức và suy diễn là hai thành phần trong bất kỳ một hệ dựa trên tri

thức nào. Phương pháp biểu diễn tri thức sẽ quyết định phương pháp suy diễn
tương ứng, nhưng ngược lại phương pháp suy diễn chỉ có thể phù hợp cho một
phương pháp biểu diễn tri thức nhất định.

6.1. Tri thức và dữ liệu

- Tri thức: là sự hiểu biết về một miền chủ đề (lĩnh vực) nào đó.

Ví dụ: Hiểu biết về y học, văn học,.... là tri thức

- Người ta thường phân loại tri thức ra làm các dạng như sau :

+ Tri thức sự kiện : là các khẳng định về một sự kiện, khái niệm nào đó

(trong một phạm vi xác định). Các định luật vật lý, toán học, ... thường được
xếp vào loại này. (Chẳng hạn : mặt trời mọc ở đằng đông, tam giác đều có 3 góc
60

, ...)

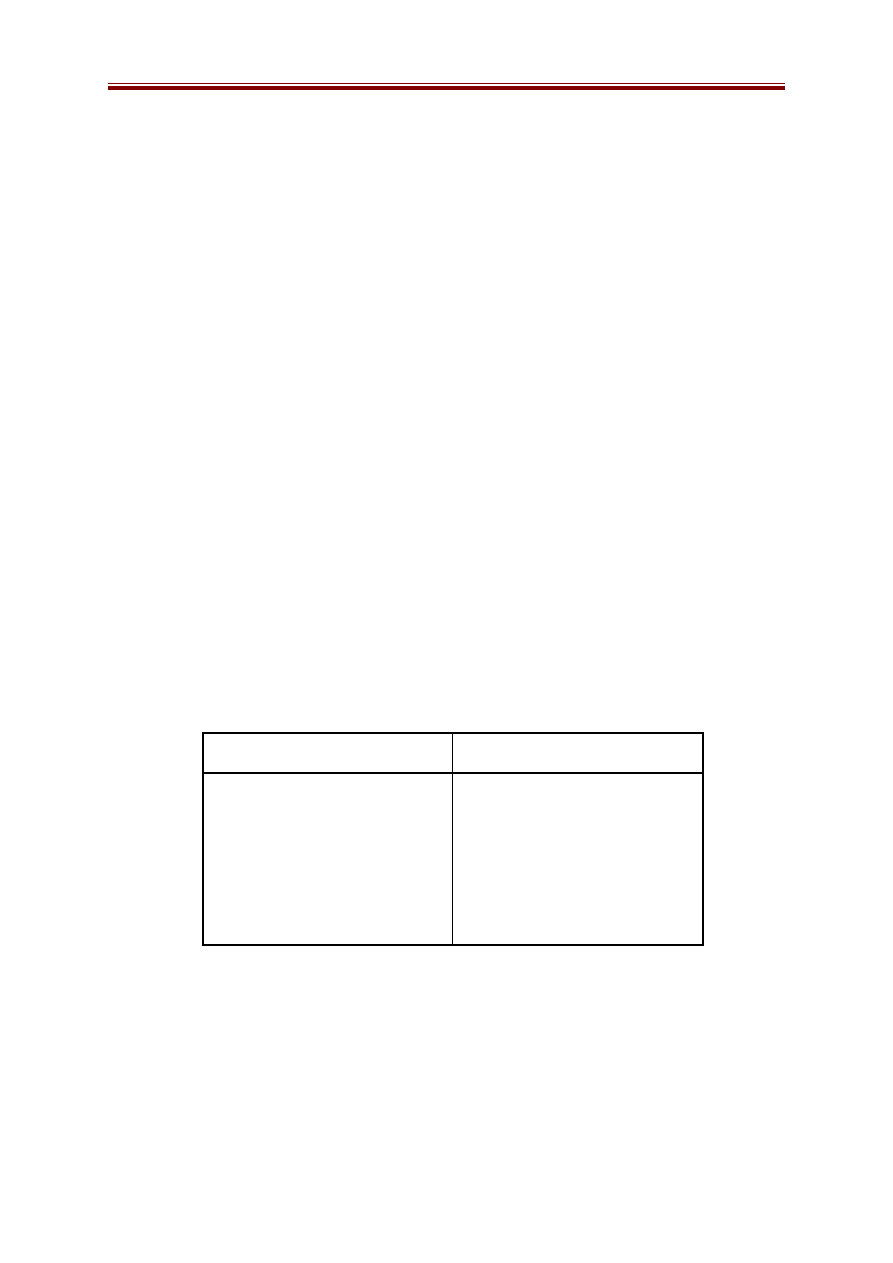
Trí tuệ nhân tạo

+ Tri thức thủ tục : thường dùng để diễn tả phương pháp, các bước cần

tiến hành, trình từ hay ngắn gọn là cách giải quyết một vấn đề. Thuật toán, thuật
giải là một dạng của tri thức thủ tục.

+ Tri thức mô tả : cho biết một đối tượng, sự kiện, vấn đề, khái niệm, ...

được thấy, cảm nhận, cấu tạo như thế nào (một cái bàn thường có 4 chân, con
người có 2 tay, 2 mắt,...)

+ Tri thức Heuristic : là một dạng tri thức cảm tính. Các tri thức thuộc

loại này thường có dạng ước lượng, phỏng đoán, và thường được hình thành
thông qua kinh nghiệm.

- Thu thập thông tin ta được dữ liệu và căn cứ vào tri thức ta có được

những quyết định phán đoán.

Ví dụ: Đối với quả cam ta xét các dữ liệu như vỏ, cuống, màu sắc,...của

nó như thế nào? và dựa vào hiểu biết của ta mà xác định xem quả cam đó là
ngon hay không ngon, ngon vừa,...

Như vậy, tri thức là dạng dữ liệu bậc cao. Khó phân biệt giữa tri thức và

dữ liệu (không có ranh giới rõ ràng giữa chúng). Tuy nhiên ta có thể phân biệt
theo bảng sau:

Dữ liệu

Tri thức

- Định lượng

- Có cấu trúc đơn giản

- Ở dạng đơn giản

- Định tính

- Không có cấu trúc hoặc
có cấu trúc phức hợp
- Ở dạng phức hợp

- So với chương trình truyền thống (được cấu tạo từ hai "chất liệu" cơ bản

là dữ liệu và thuật toán), chương trình trí tuệ nhân tạo được cấu tạo từ hai thành
phần là cơ sở tri thức (knowledge base) và động cơ suy diễn (inference engine).

+ Cơ sở tri thức : là tập hợp các tri thức liên quan đến vấn đề mà chương

trình quan tâm giải quyết.

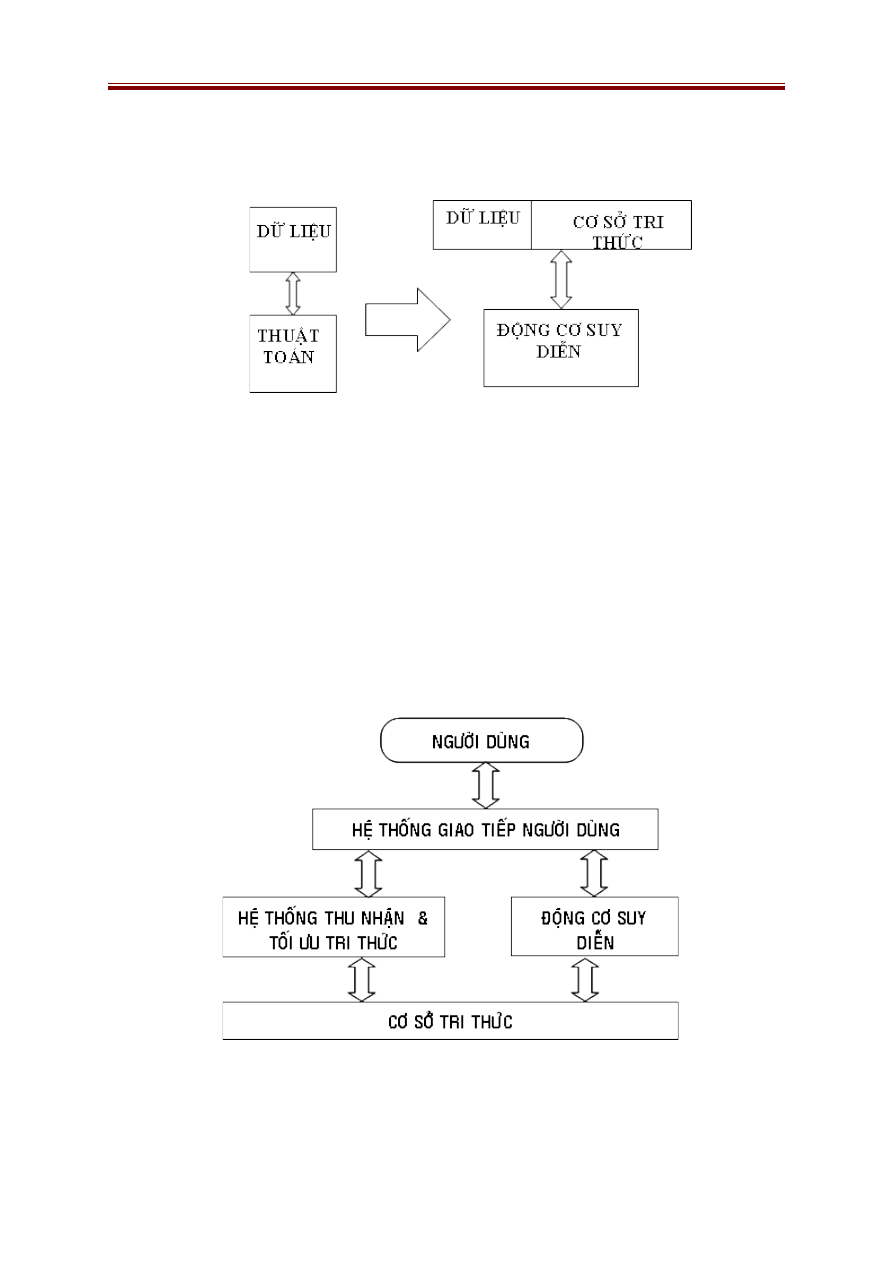
Trí tuệ nhân tạo

+ Động cơ suy diễn : là phương pháp vận dụng tri thức trong cơ sở tri

thức để giải quyết vấn đề.

Nếu xét theo quan niệm biểu diễn tri thức thì cơ sở tri thức chỉ là một

dạng dữ liệu đặc biệt và động cơ suy diễn cũng chỉ là một dạng của thuật toán
đặc biệt mà thôi. Tuy vậy, có thể nói rằng, cơ sở tri thức và động cơ suy diễn là
một bước tiến hóa mới của dữ liệu và thuật toán của chương trình! Bạn có thể
hình dung động cơ suy diễn giống như một loại động cơ tổng quát, được chuẩn
hóa có thể dùng để vận hành nhiều loại xe máy khác nhau và cơ sở tri thức
chính là loại nhiên liệu đặc biệt để vận hành loại động cơ này !

Cấu trúc chung nhất của một chương trình trí tuệ nhân tạo

6.2. Các phương pháp biểu diễn tri thức (mô tả tri thức)

Để máy tính có thể sử dụng được tri thức, có thể xử lý được tri thức,

chúng ta cần phải biểu diễn tri thức dưới dạng thuận tiện cho máy tính. Đó là

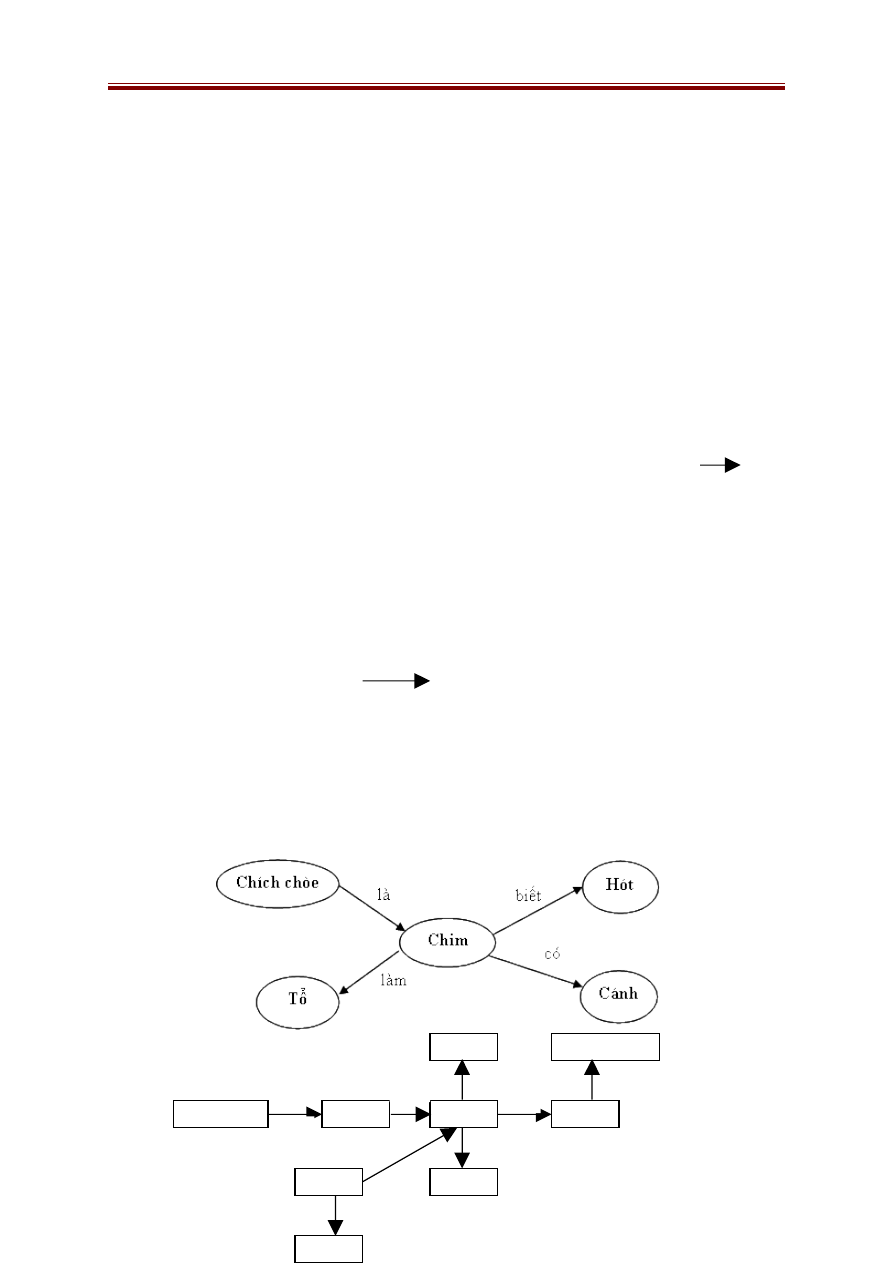
Trí tuệ nhân tạo

mục tiêu của biểu diễn tri thức. Sau nhiều cố gắng, các nhà TTNT đã phát triển
một số cách biểu diễn (thể hiện) tri thức có hiệu quả trong máy.

6.2.1. Biểu diễn tri thức nhờ logic

Như ta đã nghiên cứu ở chương 5, ta có thể biểu diễn bài toán bằng các

biểu thức logic (logic mệnh đề, logic vị từ).

6.2.2. Biểu diễn tri thức nhờ mạng ngữ nghĩa

Dùng một đồ thị G = (V, E) gồm tập đỉnh V và tập cung E. Trong đó,

đỉnh (nút mạng) là các đối tượng, các sự kiện cụ thể, cung là mối liên hệ giữa
các đối tượng, sự kiện với nhau.

Có một cung nối giữa hai đối tượng a và đối tượng b, ký hiệu a b

nếu có một quan hệ nào đó giữa hai đối tượng a, b.

Có 2 loại quan hệ đặc biệt:

- "a là b" nghĩa là đối tượng a thuộc vào tập đối tượng được biểu diễn bởi

khái niệm b hoặc tập các đối tượng biểu diễn bởi khái niệm a là tập con của tập
đối tượng biểu diễn khái niệm b (quan hệ is-a).

Ví dụ:

Yến

chim

- Ngược lại với quan hệ "là" là quan hệ "bao gồm". Khi có <a là b> (hoặc

"b bao gồm a"), các thông tin cơ bản về các đối tượng được cho bởi b sẽ truyền
lại cho a (nghĩa là a được thừa hưởng những gì b có).

Ví dụ:

cánh

Chim

bay

Con vật

Yến

Chíp chíp

Cánh cụt

đi

Không khí

is-a

hoạt động

thở

có

Trí tuệ nhân tạo

Ưu điểm:

- Cho phép biểu diễn một cách trực quan các sự kiện và các mối liên hệ

giữa chúng.

- Tính mô đun cao theo nghĩa các tri thức mới được thêm vào hoàn toàn

độc lập với các tri thức cũ.

- Là ngôn ngữ biểu diễn dạng mô tả.

- Có thể áp dụng một số cơ chế suy diễn trên mạng: cơ chế truyền và thừa

hưởng thông tin giữa các đối tượng (tính kế thừa), cơ chế "cháy" trên mạng.

Nhược điểm:

- Không có một phương pháp suy diễn chung nào cho mọi loại mạng ngữ

nghĩa.

- Khó kiểm soát quá trình cập nhật tri thức để dẫn đến mâu thuẫn trong cơ

sở tri thức.

6.2.3. Biểu diễn tri thức bằng khung (Frame)

Khung thực chất là sự tổng quát hoá của cấu trúc bản ghi trong Pascal và

tương tự như cấu trúc đối tượng trong C

Một khung được mô tả bởi cấu trúc:

- Tên khung: Định danh đối tượng mô tả.

Trí tuệ nhân tạo

- Các khe (slot): trên mỗi khe lưu trữ các thông tin, miền giá trị, thuộc
tính và chiều mũi tên chỉ đến các khung khác.

Ví dụ: Xét khung (frame) mô tả tập học sinh HOCSINH

Frame HOCSINH

IS-A:

PART-OF: NGUOI-DI-HOC

A KIND OF: (HOCSINHCOSO, HOCSINHTRUNGHOC)

Cân nặng: 10-60kg

Chiều cao: 80-170cm

Cấu trúc frame này cho ta một "khung dữ liệu" để khoanh vùng các đối

tượng là học sinh. Trường hợp gặp một người cao 175cm, nặng 45kg thì ta có
thể khẳng định rằng đó không phải là học sinh vì không thoã mãn các ràng buộc
đã có.

Ngoài ra, một trong những đặc trưng quan trọng của frame là khả năng

thừa kế các thông tin của các khe có cùng tên ở đối tượng bậc trên.

Ví dụ: Trong frame HOCSINHCOSO, HOCSINHTRUNGHOC có khe

chiều cao với giá trị mô tả miền, thì sau khi thừa kế thông tin ở mức trên Frame
HOCSINH, khe này cần phải lấy các giá trị trong khoảng 80-170cm.

6.2.4. Biểu diễn tri thức nhờ các luật sản xuất

Phương pháp biểu diễn tri thức nhờ logic (logic mệnh đề và logic vị từ)

khá trực quan song chỉ phù hợp khi không có quá nhiều luật suy diễn.

Một tri thức được thể hiện bằng một câu Horn dạng chuẩn:

∧

....

∧

⇒

Các câu Horn dạng này còn được gọi là luật if- then (luật nếu - thì) và

được biểu diễn như sau:

if P

and....and P

then Q

Trí tuệ nhân tạo

Các P

(i = 1, ..., n) được gọi là các điều kiện, Q được gọi là kết luận của

luật.

Một câu Horn dạng tổng quát:

∧

....

∧

⇒

∨

....

∨

Lưu ý:

Nếu có luật dạng: p

∧

....

∧

⇒

∨

....

∨

thì tương đương với m

luật sau:

∧

....

∧

....

∧

⇒

∧

....

∧

...

∧

⇒

∧

....

∧

....

∧

m-1

⇒

Tuy nhiên ta chỉ xét câu Horn dạng chuẩn (m=1)

Nếu n=0, m=1: câu Horn có dạng

⇒

q: gọi là sự kiện (fact) q.

Nếu n>0, m=1: câu Horn có dạng: p

∧

....

∧

⇒

q: gọi là luật (rule).

Trong các hệ chuyên gia, cơ sở tri thức gồm 2 phần: tập các sự kiện (facts)

và tập luật (rules).

Ví dụ:

- Ta có các luật về kinh nghiệm dự báo thời tiết:

"Chuồn chuồn bay thấp thì mưa, bay cao thì nắng, bay vừa thì râm"

a: chuồn chuồn bay thấp, b: chuồn chuồn bay cao, c: chuồn chuồn bay

vừa

d: trời mưa, e: trời nắng, f: trời râm

lúc đó ta có các luật sau:

⇒

Trí tuệ nhân tạo

- Nhiều định lý trong toán học có thể biểu diễn bởi các luật, ví dụ:

Nếu tam giác có một góc bằng 60

và tam giác có hai cạnh bằng nhau thì

tam giác đó là tam giác đều.

6.3. Suy diễn trên luật sản xuất

6.3.1. Khái niệm

Suy diễn là quá trình suy luận dựa vào các quy luật đã cho, thiết lập các

thông tin mới từ các thông tin đã biết. Suy diễn sẽ sử dụng tập sự kiện làm tiên
đề.

Các phương pháp suy diễn dần dần chuyển từ các giả thiết về các kết luận

bằng cách thêm vào giả thiết những sự kiện đã được khẳng định đúng, dựa trên
2 phương thức:

- Modus ponens:

A, A

⇒

nghĩa là nếu A đúng và A

⇒

B đúng thì B cũng đúng

- Modus tollens

B, A

⇒

nghĩa là nếu B sai và biết rằng A

⇒

B đúng thì A cũng sai.

Trong quá trình suy diễn, ta cần quan tâm đến các vấn đề sau:

- Xây dựng tập luật, câu hỏi nào được chọn để người sử dụng trả lời?

- Chọn quá trình tìm kiếm như thế nào?

- Thông tin nhận được có ảnh hưởng đến quá trình tìm kiếm không?

6.3.2. Bài toán

Cho tập sự kiện F= {f

, f

,...,f

} và tập luật R= {r

, r

,...,r

}. Chứng minh

tập kết luận G đúng.

6.3.3. Các phương pháp suy diễn

Trí tuệ nhân tạo

6.3.3.1. Suy diễn tiến (lập luận tiến - forward chaining hoặc forward

reasoning)

(Tư tưởng cơ bản của suy diễn tiến là áp dụng luật suy diễn Modus Ponens

tổng quát)

Là quá trình suy diễn bắt đầu từ tập sự kiện đã biết, rút ra những sự kiện

mới và cứ như vậy cho đến khi có được sự kiện cần chứng minh hoặc không có
luật nào sinh ra các sự kiện mới (tập sự kiện đúng là cực đại).

* Phương pháp:
GỌi T là tập các sự kiện (mệnh đề) tại thời điểm đang xét (khởi tạo tập

T=F: tập sự kiện đúng ban đầu ).

Xét các luật r

có dạng: p

∧

....

∧

⇒

q và p

∈

∀

nghĩa là left

)

∈

thì T= T+ right (r

)

quá trình lặp lại cho đến khi G

⊂

T hoặc không có luật nào sinh ra thêm

sự kiện mới.

* Giải thuật:

Procedure suydientien;

Begin

T:= F;
S:= loc(R, T);{ S: là tập luật có dạng p

∧

....

∧

⇒

q sao cho p

∈

∀

}

While G

⊄

T and S<>

Begin

r := get(S);
T:= T + right(r);
R:=R \ {r};
S:= loc(R,T);

End;

If G

⊂

T then write (“thành công”)

Else write (“không thành công”);

End;

* Ví dụ:

Cho trước tập sự kiện F={a,b}. Sử dụng các luật:
r

: a

⇒

: b

⇒

100

Trí tuệ nhân tạo

: c

⇒

: a

∧

⇒

: b

∧

⇒

: e

∧

⇒

cần suy ra g
Giải: Ta thể hiện trên bảng sau:

a, b
a, b, c
a, b, c, d
a, b, c, d, e
a, b, c, d, e
a, b, c, d, e, f
a. b, c, d, e, f, g

, r

Vậy g

∈

T nên bài toán được chứng minh (g: true).

* Nhận xét:
Quá trình suy diễn tiến là quá trình xem xét các luật, với mỗi luật ta xét

phần điều kiện (ở vế trái) tới phần kết luận (ở vế phải) và khi mà tất cả các điều
kiện của luật đều thoã mãn thì ta suy ra sự kiện trong phần kết luận. Chính vì lẽ
đó mà có tên là suy diễn tiến.

Trong mỗi bước của thủ tục, người ta xét một luật trong tập luật. So sánh

mỗi điều kiện (ở vế trái) của tập luật với các sự kiện trong cơ sở sự kiện, nếu tất
cả các điều kiện của luật được thoã mãn thì sự kiện trong phần kết luận được
xem là sự kiện được suy ra. Nếu sự kiện này là sự kiện mới (không có trong bộ
nhớ làm việc) thì nó được đưa vào bộ nhớ làm việc. Quá trình trên cứ lặp lại cho
đến khi nào không có luật nào sinh ra sự kiện mới.

Quá trình suy diễn tiến không định hướng tới giải quyết một vấn đề nào

cả, không hướng tới tìm ra câu trả lời cho một câu hỏi nào cả. Suy diễn tiến chỉ
là quá trình suy ra các sự kiện mới từ các sự kiện có trong bộ nhớ làm việc.

6.3.3.2. Suy diễn lùi (lập luận lùi - backward chaining hoặc backward

reason)

Là quá trình xuất phát từ sự kiện cần chứng minh và thay vào đó là những

sự kiện ở vế trái của 1 luật có vế phải là sự kiện cần chứng minh. Quá trình này
được thực hiện cho đến khi đưa về các sự kiện là tập sự kiện con của tập sự kiện

101

Trí tuệ nhân tạo

giả thiết. (Nghĩa là: để đưa ra kết luận b, ta thử tìm tất cả các luật có dạng: a

∧

....

∧

⇒

b, để có b, phải đưa ra các kết luận a

,...,a

. Quá trình xác định a

cũng

tương tự như đối với b, nếu đến một lúc nào đó phát hiện được rằng có một a

nào đó không dẫn xuất được từ các giả thiết thì quay lui sang các luật sản xuất
khác sinh ra b có dạng b

∧

....

∧

⇒

b. Ngược lại, nếu mọi a

đều dẫn xuất được

giả thiết thì quá trình dẫn xuất ra b là đúng)

* Giải thuật:
GỌi T là tập các sự kiện cần chứng minh tại thời điểm đang xét (khởi tạo

T= G, G là tập kết luận).

S(p) ={r

∈

R / right(r

) = p} ( là tập các luật trong R sao cho vế phải chứa p)

Procedure suydienlui (g);

Begin
T:= {g};
If T

⊂

F then write (‘g đã được chứng minh ‘)

Else

Begin

p:=get(T);

If S(p) = {} then write (‘g không chứng minh được ‘)

Else

For r

∈

S(p) do

Begin

T:= T \ right(r

);

T:= T + left(r

);

For l

∈

T \ F do suydienlui(l);

End;

* Ví dụ:
Cho tập sự kiện F={p, r}, và tập luật R:
r

: p

⇒

: q

∧

⇒

Chứng minh s

S(p)

s
q

s
q, r
r, p

6.3.4. Nhận xét

102

Trí tuệ nhân tạo

- Suy diễn tiến
Ưu điểm:

+ Làm việc tốt khi bài toán có bản chất là đi thu thập thông tin rồi thấy

điều cần suy diễn.

+ Cho ra khối lượng lớn các thông tin từ một số thông tin ban đầu. Nó

sinh ra nhiều thông tin mới.

+ Suy diễn tiến là tiếp cận lý tưởng đối với các loại bài toán cần giải

quyết các nhiệm vụ như lập kế hoạch, điều hành, điều khiển và diễn dịch.

Nhược điểm:
+ Không cảm nhận được rằng chỉ cần một vài thông tin quan trọng. hệ

thống hỏi các câu hỏi có thể hỏi mà không biết rằng chỉ một ít câu đã đi đến kết
luận được.

+ Hệ thống có thể hỏi cả câu hỏi không liên quan. Có thể các câu trả lời

cũng quan trọng nhưng làm người dùng lúng túng khi phải trả lời các câu chẳng
dính đến chủ đề.
- Suy diễn lùi: Ưu điểm:

+ Phù hợp với bài toán đưa ra giả thuyết và liệu giả thuyết đó có đúng

hay không?

+ Tập trung vào đích đã cho. Nó tạo ra một loạt câu hỏi chỉ liên quan đến

vấn đề đang xét, thuận tiện đối với người dùng.

+ Khi suy diễn một điều gì từ thông tin đã biết , nó chỉ tìm trên một phần

của cơ sở tri thức thích đáng đối với bài toán đang xét.

+ Suy diễn lùi được đánh giá cao trong các bài toán như là chẩn đoán, dự

đoán và tìm lỗi.

Nhược điểm:
+ Nhược điểm cơ bản của loại suy diễn này là nó thường tiếp theo dòng

suy diễn thay vì đúng ra phải dừng ở đó mà sang nhánh khác.

Như vậy, dựa vào các ưu và nhược điềm của từng loại suy diễn mà ta nên

chọn kỹ thuật suy diễn nào để áp dụng vào bài toán. Trước tiên, ta xem xét các
chuyên gia giải nó như thế nào?. Nếu cần thu thập dữ liệu rồi mới quyết định
suy diễn cái gì thì ta chọn suy diễn tiến. còn nếu đã có giử thuyết và cần chứng
minh cái đích này thì ta dùng suy diễn lùi.

Ví dụ: Một bác sĩ có thể hiểu hàng trăm vấn đề có thể xảy ra với một cá

nhân, nhưng vẫn phải tìm hiểu hiện trạng của bệnh nhân, lúc đó cần suy diễn

103

Trí tuệ nhân tạo

tiến. Nguợc lại bác sĩ hầu như thấy được bệnh (ví dụ như viêm họng) thì ông ta dùng
suy diễn lùi.

104

Document Outline

Chú ý:

Wyszukiwarka

Podobne podstrony:

więcej podobnych podstron

Trí Tuệ Nhân Tạo Nhiều Tác Giả, 104 Trang

Document Outline