
Janusz Kacerka
Dyskretne Układy
Regulacji
————————————————————————————————————————
Semestr 5 Elektrotechnika
Rozdział 3 - 4

Spis treści
PIS UKŁADÓW DYSKRETNYCH W PRZESTRZENI STANÓW
YBRANE WŁAŚCIWOŚCI PRZEKSZTAŁCENIA
2
Dyskretne Układy Regulacji

Rozdział 3
3. Funkcje dyskretne i równania różnicowe
Do analizy i syntezy układów dyskretnych stosuje się funkcje dyskretne a w przypadku
liniowych układów stacjonarnych wykorzystuje się przekształcenie Z.
3.1 Funkcje dyskretne
Z dowolnej funkcji ciągłej y(t) można otrzymać funkcję dyskretną y(kT
s
). Operację taką
przedstawiono jako wynik działania idealnego klucza (rys.2.3). Dla uproszczenia zapisu i
zwykle z tego powodu, że okres impulsowania jest zadany i stały dla całego układu funkcje
dyskretna zapisuje się w postaci y(k), opuszczając oznaczenie T
s
.
3
Dyskretne Układy Regulacji
Ponieważ w układach dyskretnych operuje się na funkcjach dyskretnych, to nie można
stosować zwykłych pochodnych i równań różniczkowych. Analogiem pochodnej funkcji
ciągłej w układach dyskretnych jest różnica funkcji dyskretnej określona wzorem
Rozdział 3
( ) (
) ( )
k
y
k
y
k
y
−
+
=
Δ
1
(3.1)
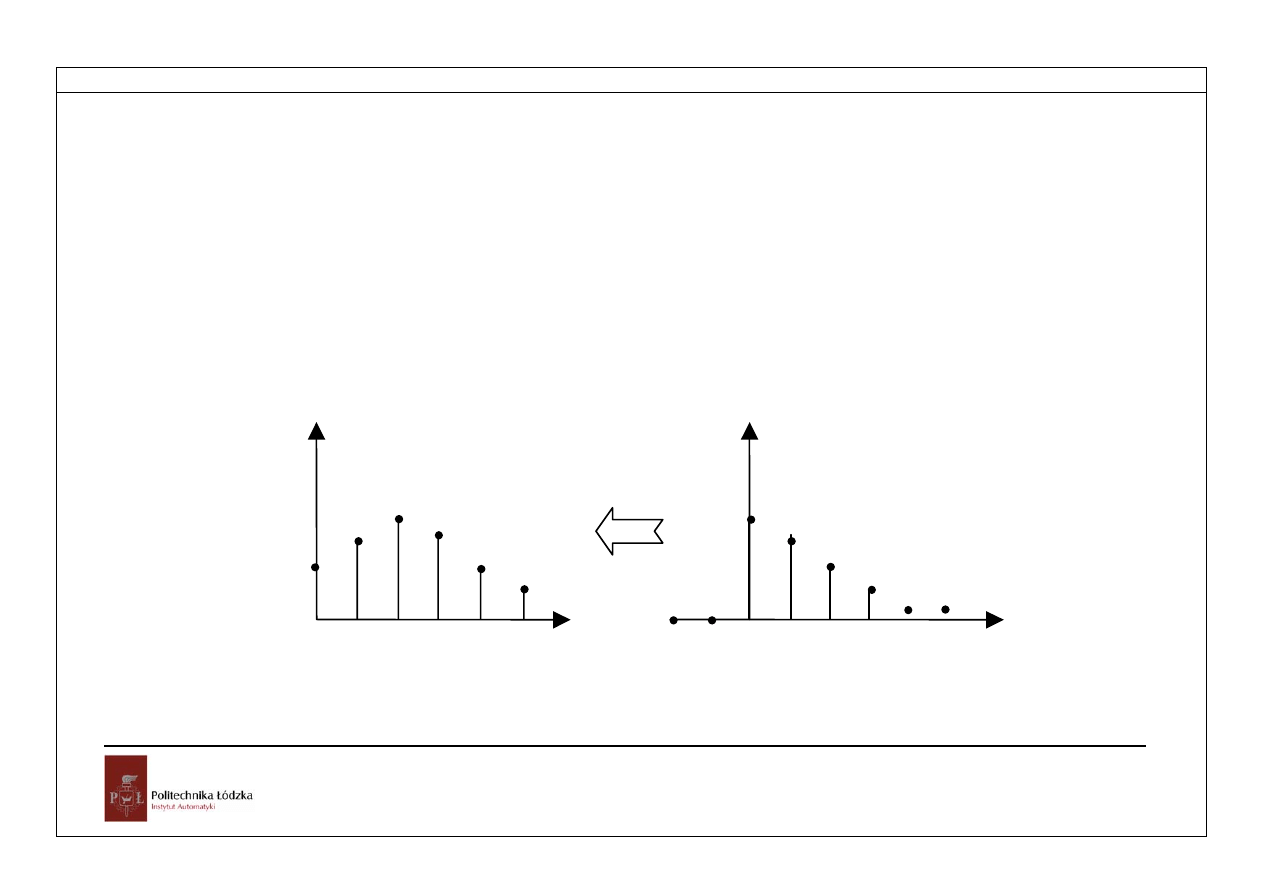
We wzorze wprowadzono funkcję przesuniętą względem chwili k. Funkcje dyskretne
mogą być przesunięte w lewo (przyspieszone) o zadaną liczbę okresów impulsowania albo
w prawo (opóźnione).
y(k)
0 1
2
3
4
k
5
y(k)
3
4
k
5
0 1 2
4
Dyskretne Układy Regulacji
Rys.3.1. Funkcja dyskretna przesunięta w lewo o 2 okresy – y(k+2)
Rozdział 3
y(k)
0 1
2
3
4
k
5
y(k)
3
4
k
5
0
1 2
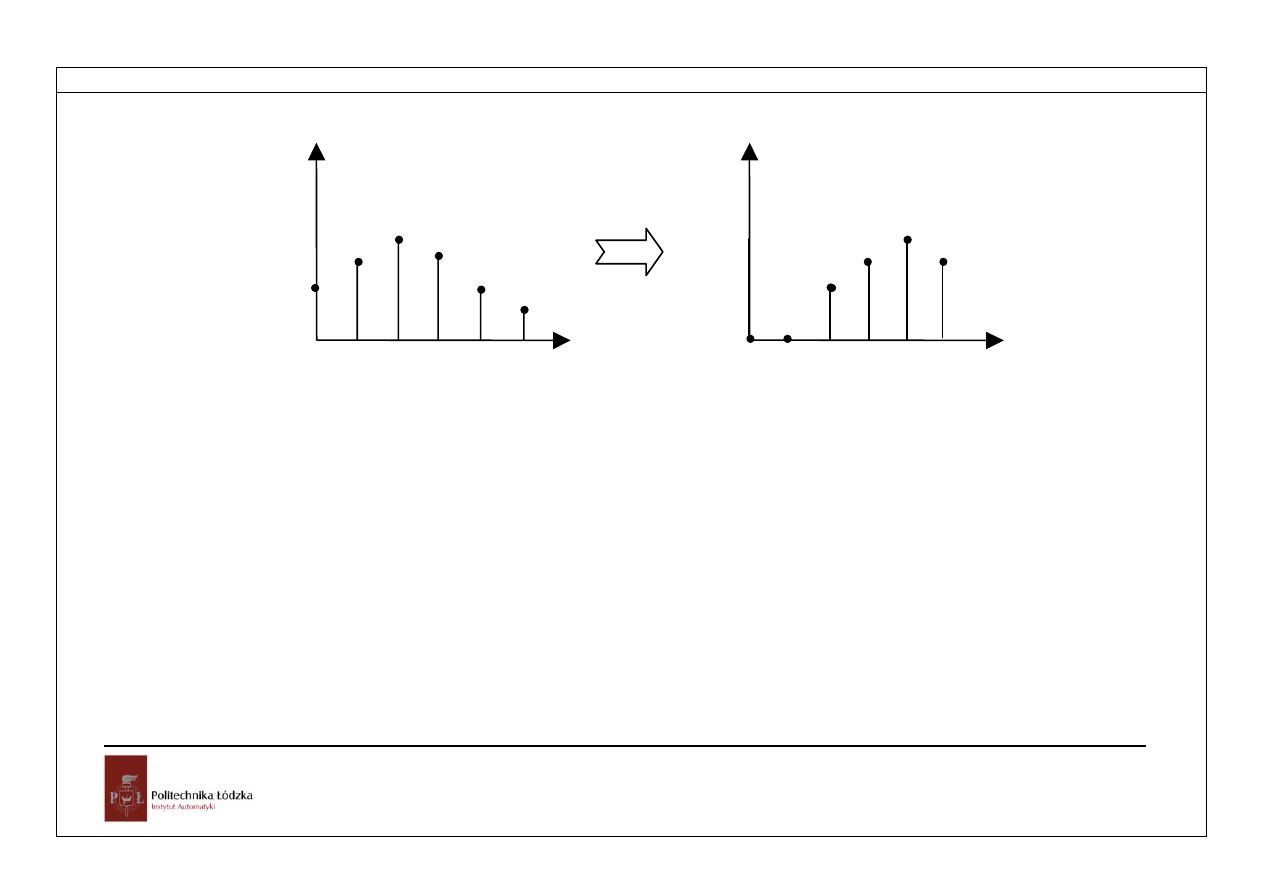
Rys.3.2. Funkcja dyskretna przesunięta w prawo o 2 okresy – y(k-2)
Podobnie jak w układach ciągłych pochodne wyższych rzędów tak i tutaj występują
różnice wyższych rzędów
( )
(
)
( ) (
) (
) (
) ( ) (
)
(
) ( )
k
y
k
y
k
y
k
y
k
y
k
y
k
y
k
y
k
y
k
y
+
+
−
+
=
+
+
−
+
−
+
=
Δ
−
+
Δ
=
Δ
1
2
2
1
1
2
1
2
(3.2)
( )
(
)
( ) (
)
(
)
(
) ( )
k
y
k
y
k
y
k
y
k
y
k
y
k
y
−
+
+
+
−
+
=
Δ
−
+
Δ
=
Δ
1
3
2
3
3
1
2
2
3
(3.3)
5
Dyskretne Układy Regulacji
i ogólnie różnica rzędu n

Rozdział 3
( )
(
)
( )
k
y
k
y
k
y
n
n
n
Δ
−
+
Δ
=
Δ
−
1
1
(3.4)
Układ dyskretny można opisać równaniem różnicowym postaci
( )
( )
( )
( )
( )
( )
( )
( )
k
u
b
k
u
b
k
u
b
k
u
b
k
y
a
k
y
a
k
y
a
k
y
a
q
q
q
q
p
p
p
p
0
1
1
1
0
1
1
1
,
,
,
,
,
,
+
Δ
+
+
Δ
+
Δ
=
=
+
Δ
+
+
Δ
+
Δ
−
−
−
−
(3.5)
gdzie y – dyskretny sygnał wyjściowy, u - dyskretny sygnał wejściowy, p
≥q
Ze względu na możliwość operowania funkcjami przesuniętymi równanie przedstawia
się także w postaci
(
)
(
)
k
n
u
d
k
n
y
c
q
k
k
p
k
k
+
=
+
∑
∑
=
=
0
0
(3.6)
6
Dyskretne Układy Regulacji
Rozwiązanie równania wymaga p wartości sygnałów y tj. y(0),y(1)...y(p-1) i znanego
przebiegu sygnału wejściowego u(n)

Rozdział 3
3.2 Opis układów dyskretnych w przestrzeni stanów
Równania dyskretne obiektu mogą być także przedstawione w przestrzeni stanów.
Systemem (układem) dynamicznym, liniowym, stacjonarnym, dyskretnym nazywa się
system, którego funkcja stanu jest rozwiązaniem równania różnicowego
(
)
( )
( )
( )
( )
0
,
1
0
x
k
x
k
Bu
k
Ax
k
x
k
=
+
=
+
=
(3.7)
i którego funkcja wyjścia jest określona liniowym równaniem algebraicznym
( )
( )
( )
k
Du
k
Cx
k
y
+
=
,
(3.8)
gdzie:
x(k)
∈ R
n
– wektor stanu układu,
u(k)
∈ R
p
– wektor wejścia układu,
y(k)
∈ R
m
– wektor wyjścia układu,
7
Dyskretne Układy Regulacji
A,B,C,D – macierze rzeczywiste,

Rozdział 3
równanie (1) – równanie stanu,
równanie (2) – równanie wyjścia,
n – stopień równania stanu,
p – liczba wejść,
m – liczba wyjść,
k – indeks skalarny, przyjmujący wartości całkowite dodatnie reprezentuje kolejne
dyskretne momenty czasu [12]
(
)
[
]
( ) ( )
( ) ( )
i
i
i
i
i
kT
u
kT
B
kT
x
kT
A
T
k
x
+
=
+ 1
(3.9)
[ ]
( ) ( )
( ) ( )
i
i
i
i
i
kT
u
kT
D
kT
x
kT
C
kT
y
+
=
(3.10)
8
Dyskretne Układy Regulacji
Równania (3.9),(3.10) są równaniami różnicowymi układów liniowych niestacjonarnych z
uwzględnieniem okresu impulsowania T
i
. Okres impulsowania oznacza się także T
s
(sample
Rozdział 3
time)
(
)
( ) ( )
( ) ( )
k
u
k
B
k
x
k
A
k
x
+
=
+ 1
(3.11)
( )
( ) ( )
( ) ( )
k
u
k
D
k
x
k
C
k
y
+
=
(3.12)
Równania (3.11) i (3.12) są równaniami różnicowymi układów liniowych
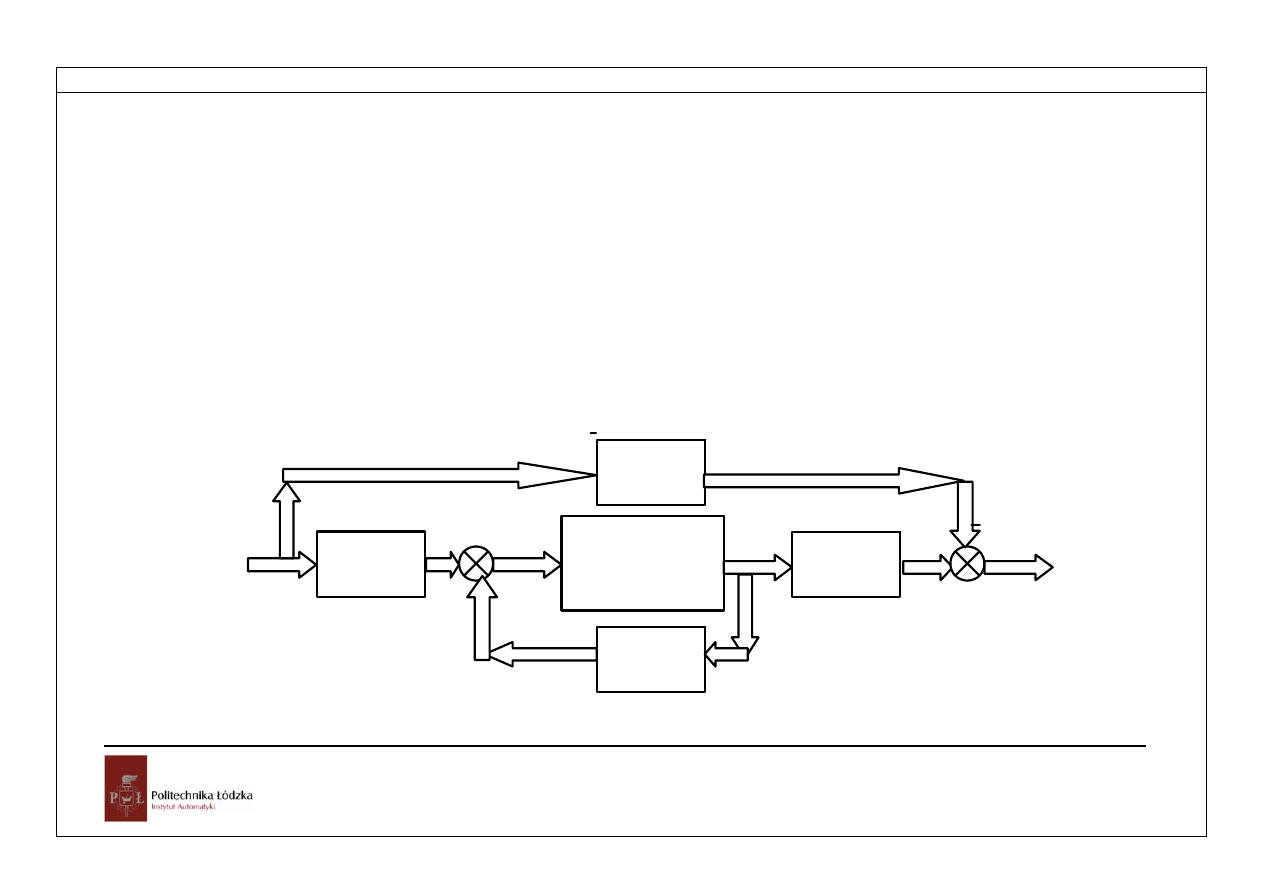
niestacjonarnych z domyślnym okresem impulsowania. Na rysunku 3.3 przedstawiono
schemat blokowy niestacjonarnego układu dyskretnego.
9
Dyskretne Układy Regulacji
y(k)
B(k)
C(k)
D(k)
A(k)
u(k)
x(k+1)
Opóźnienie
T
i
x(k)

Rozdział 3
Rys.3.3.Schemat blokowy liniowego, niestacjonarnego, dyskretnego układu sterowania
Na schemacie zaznaczono człon opóźniający o jeden okres impulsowania. Wynika to
z zasady obliczeń, wymagających pamiętania poprzednich stanów (Przykład 2.1).
Przedstawione równania są równaniami dotyczącymi bardzo ogólnych przypadków,
gdzie występuje więcej wejść i wyjść niż jedno (układy MIMO). W układach omawianych
na wykładzie najczęściej występuje jedno wejście i jedno wyjście (układy SISO).
Przykład 3.1
Dane jest równanie różnicowe układu z jednym wejściem i jednym wyjściem
(
)
(
)
(
)
( )
)
(
1
2
3
0
0
1
2
k
u
b
k
y
a
k
y
a
k
y
a
k
y
=
+
+
+
+
+
+
(3.13)
10
Dyskretne Układy Regulacji
Przedstawić równanie w przestrzeni stanów, przyjmując zmienną stanu x
1
(k)=y(k) oraz

Rozdział 3
( )
(
) (
)
( )
(
) (
)
2
1
1
1
2
3
1
2
+
=
+
=
+
=
+
=
k
y
k
x
k
x
k
y
k
x
k
x
(3.14)
Wyjściowe równanie różnicowe można wówczas zapisać w następujący sposób
(
)
( )
(
)
( )
(
)
( )
( )
( )
( )
( )
k
x
k
y
k
u
b
k
x
a
k
x
a
k
x
a
k
x
k
x
k
x
k
x
k
x
1
0
3
2
2
1
1
0
3
3
2
2
1
)
(
1
1
1
=
+
−
−
−
=
+
=
+
=
+
(3.15)
Macierze stanu, wejścia, wyjścia i transmisyjna przyjmą następujące postaci
(
)
( )
( ) ( )
( )
( )
[
]
[ ]
0
0
0
1
0
0
1
0
0
0
1
0
1
0
2
1
0
=
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
+
=
+
=
+
D
C
b
B
a
a
a
A
k
Du
k
Cx
k
y
k
Bu
k
Ax
k
x
(3.16)
11
Dyskretne Układy Regulacji
Równania mają ilustrację w postaci schematu blokowego
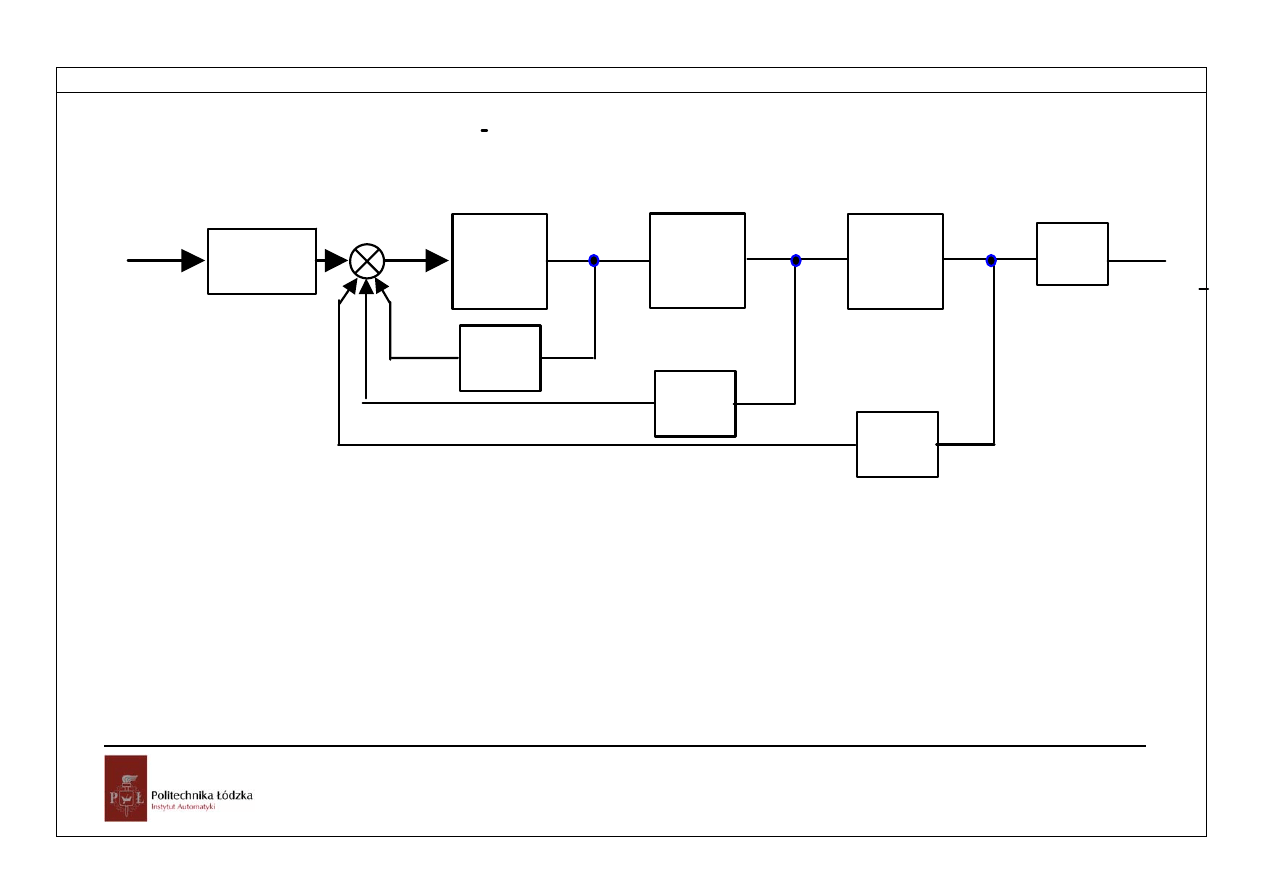
Rozdział 3
y(k)
b
0
-a
2
u(k)
x
3
(k+1)
Opóź-
nienie
T
s
Opóź-
nienie
T
s
-a
1
Opóź-
nienie
T
s
-a
0
1
x
2
(k+1)
x
1
(k+1)
x
1
(k)
x
2
(k)=
x
3
(k)=
Rys.3.3.Schemat blokowy układu z przykładu 3.1
12
Dyskretne Układy Regulacji
Rozwiązanie układu równań różnicowych liniowych można uzyskać metodą klasyczną w
następujący sposób.

Rozdział 3
Dane są warunki początkowe
( )
0
0
x
k
x
k
=
=
(3.17)
oraz wartości sygnału wejściowego u(k).
W kolejnych chwilach otrzymuje się następujące wartości
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
2
1
0
3
2
3
2
1
0
1
1
2
1
0
1
0
2
0
3
0
2
0
Bu
ABu
Bu
A
x
A
Bu
Ax
x
n
Bu
ABu
x
A
Bu
Ax
x
n
Bu
Ax
x
n
+
+
+
=
+
=
=
+
+
=
+
=
=
+
=
=
,
(3.18)
a ogólnie
( )
( )
i
Bu
A
x
A
n
x
n
i
i
i
n
n
∑
−
=
=
−
−
+
=
1
0
1
0
(3.19)
13
Dyskretne Układy Regulacji
Macierz A
n
nazywa się macierzą podstawową układu równań różnicowych.

Rozdział 3
Wyznaczanie równań różnicowych w przestrzeni stanów układów opisanych w
dziedzinie układów ciągłych za pomocą układu równań pierwszego rzędu rozpatruje się dla
dwóch przypadków
a) układ ciągły jest poprzedzony impulsatorami idealnymi (tyle impulsatorów ile wejść).
b) układ ciągły jest poprzedzony ekstrapolatorami zerowego rzędu.
Przy wyznaczaniu równań korzysta się z rozwiązania układu równań różniczkowych w
przedziale [k,k+1]. Ogólna postać rozwiązania układu równań różniczkowych o stałych
współczynnikach jest określona wzorem
( )
(
)
( )
( )
τ
τ
+
=
∫
τ
−
−
d
Bu
e
x
e
t
x
t
t
t
A
t
t
A
0
0
0
(3.20)
14
Dyskretne Układy Regulacji
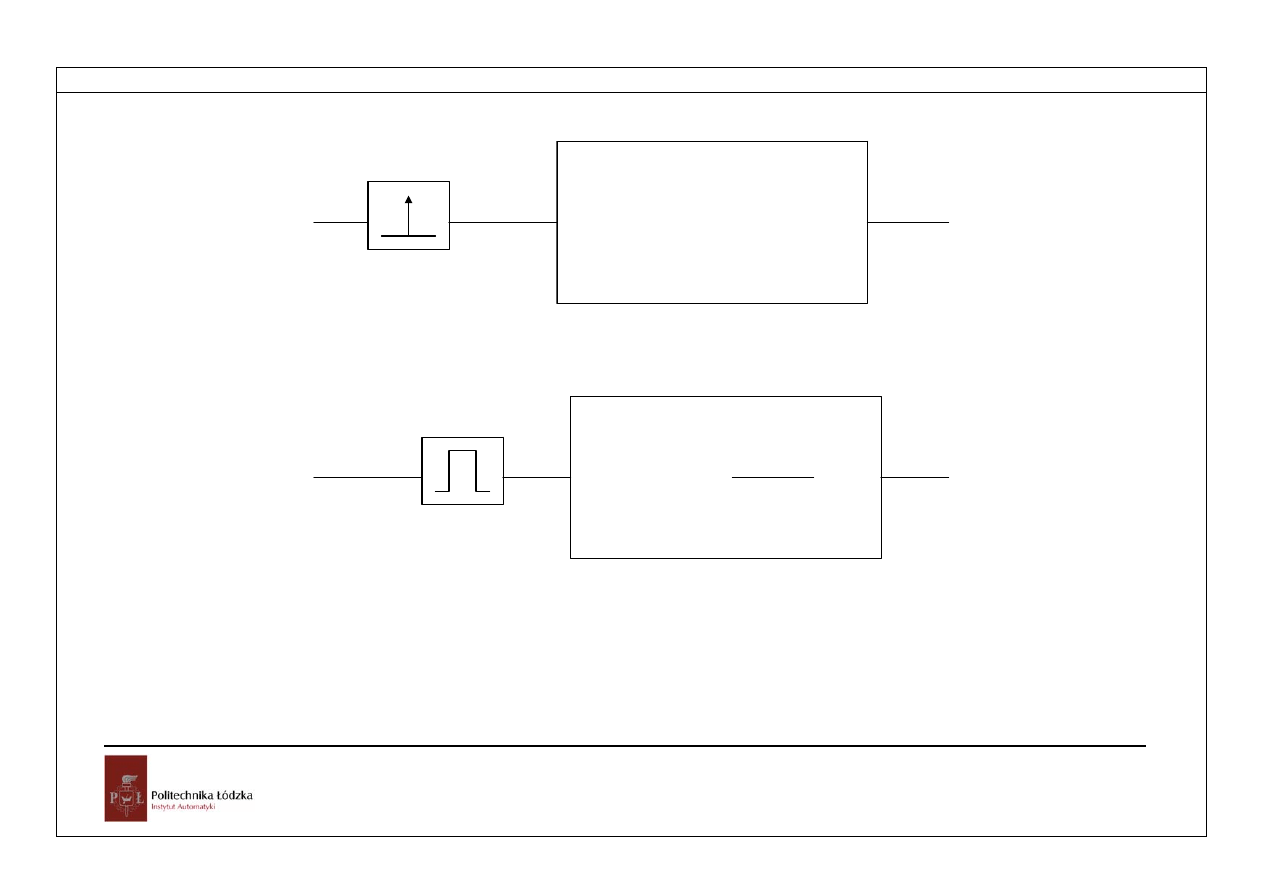
Schematy blokowe omawianych układów przedstawiono na rysunkach 3.4 i 3.5.
Rozdział 3
u
D
x
C
y
u
B
x
A
x
1
1
1
1
+
=
+
=
&
Rys.3.4.Układ ciągły opisany w przestrzeni stanów z impulsatorem idealnym
u
D
x
C
y
u
B
x
A
x
1
1
1
1
+
=
+
=
&
Ekstrapolator
zerowego
rzedu
Rys.3.5.Układ ciągły opisany w przestrzeni stanów z ekstrapolatorem
15
Dyskretne Układy Regulacji
Ciąg impulsów wyjściowych idealnego impulsatora

Rozdział 3
( ) ( ) (
)
,...
2
,
1
,
0
*
=
−
=
k
kT
t
kT
u
t
u
i
i
δ
(3.21)
We wzorze (3.20) przyjęto x
0
=x(kT
i
), t=(k+1)T
i
, t
0
=kT
i
,
Wektor stanu po upływie okresu impulsowania
(
)
[
]
( )
(
)
[
]
( )
(
)
∫
+
τ
−
+
τ
+
=
+
i
i
i
i
T
k
kT
i
T
k
A
i
T
A
i
d
kT
u
B
e
kT
x
e
T
k
x
1
1
1
1
1
1
(3.22)
Ze względu na filtrujące właściwości impulsów Diraca w całce otrzymuje się
(
)
[
]
( )
( )
i
T
A
i
T
A
i
kT
u
B
e
kT
x
e
T
k
x
i
i
1
1
1
1
+
=
+
(3.23)
Macierze układu dyskretnego
1
1
1
1
1
D
D
C
C
B
e
B
e
A
i
i
T
A
T
A
=
=
=
=
(3.24)
16
Dyskretne Układy Regulacji
Drugi z omawianych układów dotyczy impulsów prostokątnych na wyjściu elementu
formującego

Rozdział 3
(
)
[
]
( )
(
)
[
]
( )
(
)
∫
+
τ
−
+
τ
+
=
+
i
i
i
i
T
k
kT
i
T
k
A
i
T
A
i
d
kT
u
B
e
kT
x
e
T
k
x
1
1
1
1
1
1
(3.25)
Po zmianie granic całkowania otrzymuje się najpierw
(
)
[
]
( )
( )
∫
+
=
+
i
i
T
i
t
A
i
T
A
i
dt
kT
u
B
e
kT
x
e
T
k
x
0
1
1
1
1
(3.26)
a następnie macierze układu następującej postaci
[
]
1
1
1
1
1
1
1
1
D
D
C
C
B
e
A
B
e
A
i
i
T
A
T
A
=
=
−
=
=
−
(3.27)
Przykład 3.2
17
Dyskretne Układy Regulacji
Dany jest element inercyjny pierwszego rzędu, opisany równaniem

Rozdział 3
x
y
u
T
k
x
T
x
=
+
−
=
1
&
(3.28)
Należy wyznaczyć dyskretne równania stanu dla układu poprzedzonego impulsatorem
idealnym i ekstrapolatorem zerowego rzędu.
Ustalono macierze układu ciągłego. Są to
0
1
1
1
1
1
1
=
=
=
−
=
D
C
T
k
B
T
A
(3.29)
Korzystając ze wzoru (3.24) otrzymuje się
18
Dyskretne Układy Regulacji
0
1
=
=
=
=
−
−
D
C
e
T
k
B
e
A
T
T
T
T
i
i
(3.30)

Rozdział 3
W drugim przypadku skorzystano ze wzoru (3.27)
0
1
1
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
=
−
−
D
C
e
k
B
e
A
T
T
T
T
i
i
(3.27)
19
Dyskretne Układy Regulacji
W układach dyskretnych liniowych stosuje się przekształcenie Z, które umożliwia
operowanie równaniami algebraicznymi zamiast równaniami różnicowymi.

Rozdział 4
4.Przekształcenie Z
4.1 Definicja przekształcenia Z
Dla funkcji dyskretnej f(kT
s
) transformatą F(z), nazywa się sumę szeregu
nieskończonego
( )
( )
∑
∞
=
−
=
0
k
k
i
z
kT
f
z
F
(4.1)
Transformata istnieje, jeżeli szereg jest zbieżny. Zmienna z jest zmienna zespoloną.
Funkcja dyskretna f(kT
i
) albo f(k) nazywa się oryginałem dyskretnym, a f(t) –
oryginałem ciągłym.
Przykład 4.1
20
Dyskretne Układy Regulacji
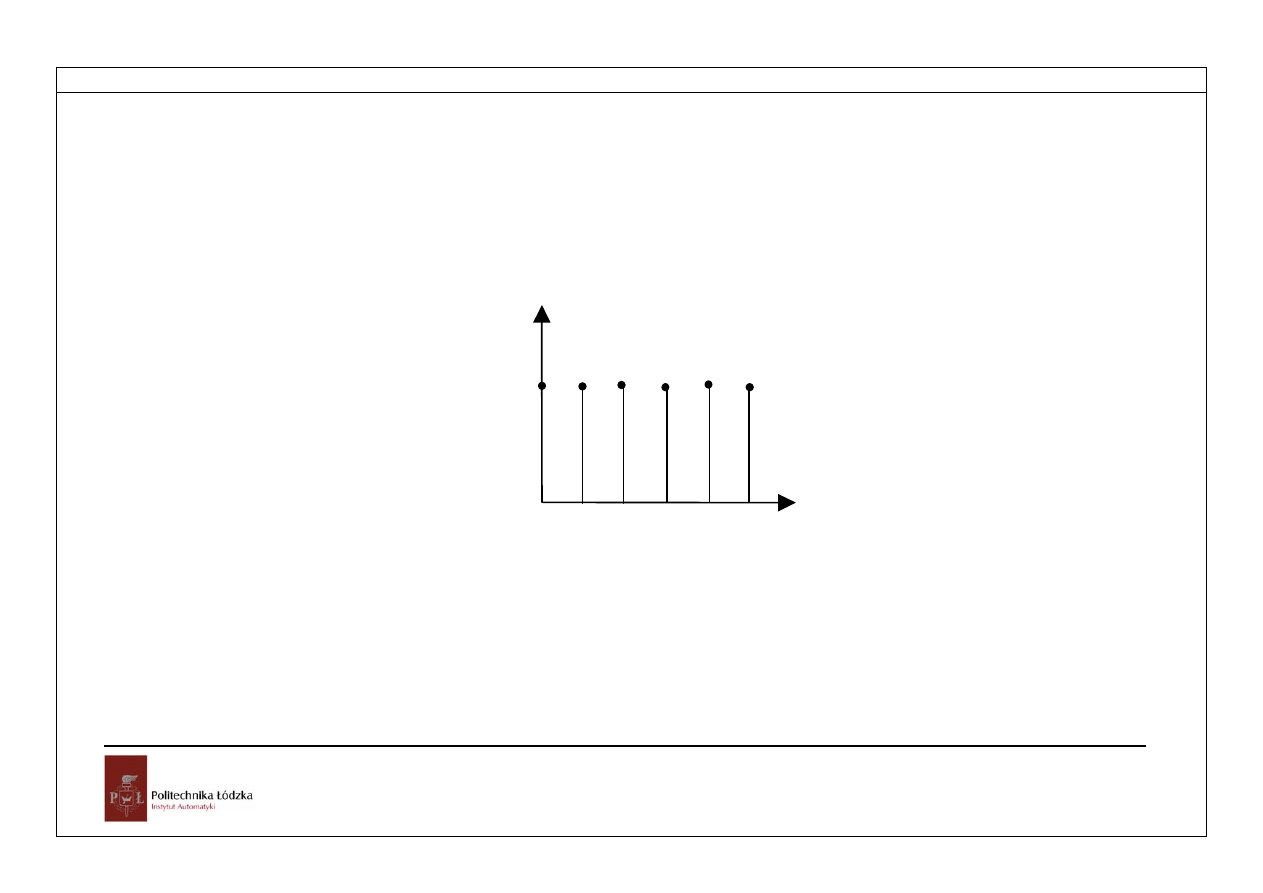
Dana jest funkcja dyskretna jednostkowa określona wzorem:
Rozdział 4
( )
⎩
⎨
⎧
<
≥
=
0
0
0
1
1
n
dla
n
dla
n
(4.2)
Jej przebieg pokazano na rysunku
1(n)
0 1
2
3
4
n
5
1
Rys.4.1.Jednostkowa funkcja dyskretna
21
Dyskretne Układy Regulacji
Suma szeregu (4.1) ma postać

Rozdział 4
( )
1
1
1
1
1
1
1
3
2
0
−
=
+
+
+
+
+
+
=
=
∑
∞
=
−
z
z
z
z
z
z
z
z
k
k
k
L
L
(4.3)
Jest to suma ciągu geometrycznego o pierwszym wyrazie 1 i ilorazie 1/z. Dla |1/z|<1
szereg jest zbieżny.
Przykład 4.2
Dana jest funkcja dyskretna wykładnicza określona wzorem
⎩
⎨
⎧
<
≥
=
α
−
α
−
0
0
0
)
(
1
n
dla
n
dla
e
n
e
i
i
nT
nT
(4.4)
22
Dyskretne Układy Regulacji
Transformata Z tej funkcji ma postać
Rozdział 4
( )
[
]
1
;
1
1
3
3
2
2
0
<
−
=
=
+
+
+
+
+
+
=
=
α
−
α
−
α
−
α
−
α
−
α
−
∞
=
−
α
−
α
−
∑
z
e
warunek
e
z
z
z
e
z
e
z
e
z
e
z
e
n
e
Z
i
i
i
i
i
i
i
i
T
T
k
kT
T
T
T
k
k
nT
nT
L
L
(4.3)
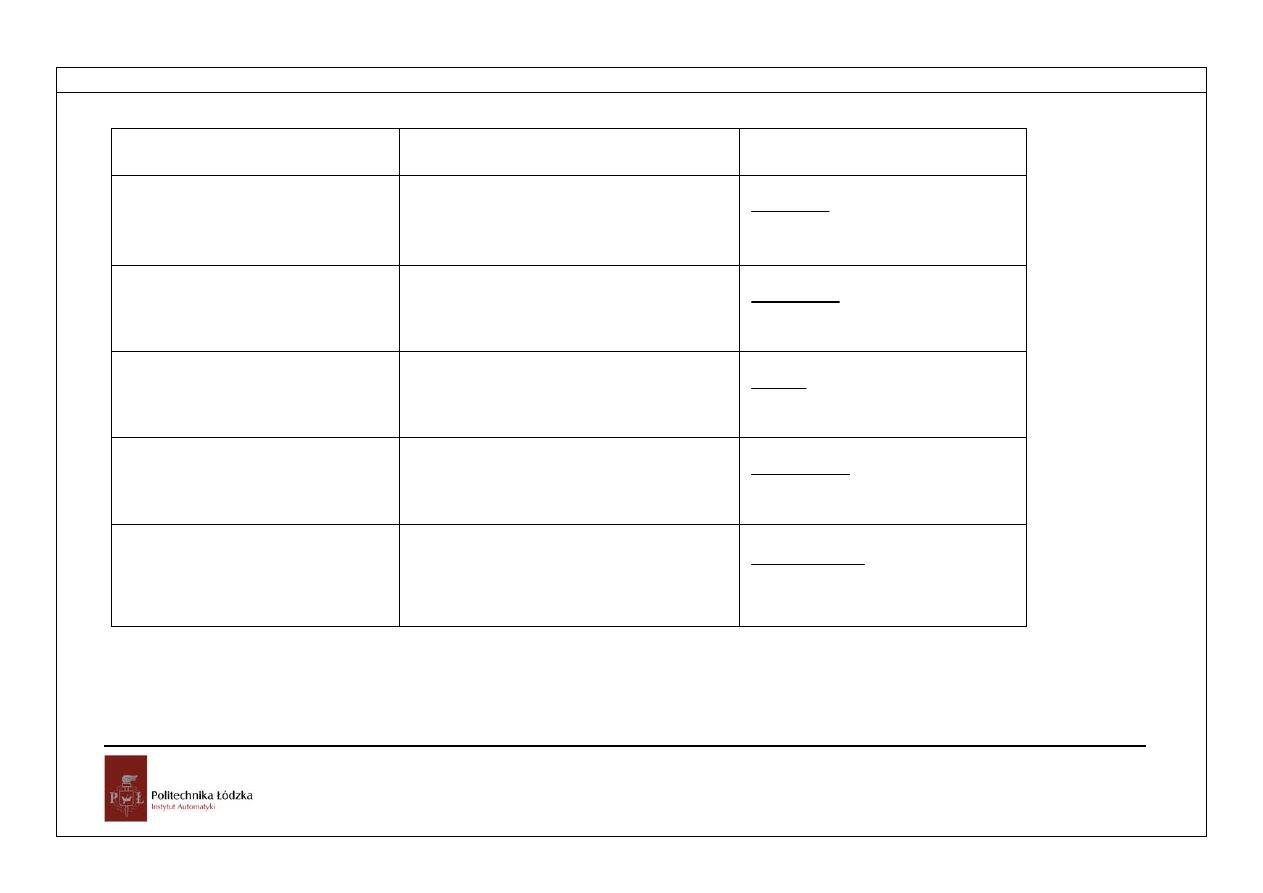
Tablica transformat wybranych funkcji
23
Dyskretne Układy Regulacji
Funkcja ciągła f(t)
Funkcja dyskretna f(n)
Transformata F(z)
)
(t
δ
( )
s
nT
δ
1
)
(t
1
)
(
s
nT
1
1
−
z
z
Rozdział 4
Funkcja ciągła f(t)
Funkcja dyskretna f(n)
Transformata F(z)
)
(t
t
1
⋅
)
(
)
(
s
s
nT
nT
1
⋅
2
)
1
(
−
⋅
z
z
T
s
)
(t
e
at
1
⋅
±
)
(
s
anT
nT
e
s
1
⋅
±
s
aT
e
z
z
±
−
)
(t
a
t
1
⋅
)
(
s
nT
nT
a
s
1
⋅
a
z
z
−
)
(
1 t
e
t
j
⋅
ω
±
)
(
1
s
nT
j
nT
e
s
⋅
ω
±
s
T
j
e
z
z
ω
±
−
)
(
1 t
te
at
⋅
−
( )
)
(
1
s
anT
s
nT
e
nT
s
⋅
−
(
)
2
s
s
aT
aT
s
e
z
e
zT
−
−
−
24
Dyskretne Układy Regulacji

Rozdział 4
4.2 Wybrane właściwości przekształcenia Z
Transformata funkcji dyskretnej przesuniętej w lewo o k okresów impulsowania
(
)
[
]
( )
( )
∑
−
=
−
−
=
+
1
0
k
i
i
k
k
z
i
f
z
F
z
k
n
f
Z
(4.4)
W przypadku szczególnym, gdy
( )
( )
(
)
0
1
1
0
=
−
=
=
=
k
f
f
f
L
(4.5)
(
)
[
]
( )
z
F
z
k
n
f
Z
k
=
+
(4.6)
Transformata funkcji opóźnionej o k okresów impulsowania
(
)
[
]
( )
z
F
z
k
n
f
Z
k
−
=
−
(4.7)
Transformata różnicy funkcji dyskretnej
( )
[
]
25
Dyskretne Układy Regulacji
(
) ( )
( )
0
1
zf
z
F
z
n
f
Z
−
−
=
Δ
(4.8)

Rozdział 4
Suma funkcji dyskretnej i jej transformata.
Suma funkcji dyskretnej jest określona wzorem
( )
∑
−
=
=
=
ϕ
1
0
)
(
n
i
i
i
f
n
(4.9)
Pierwsza różnica sumy funkcji dyskretnej jest określona wzorem
( )
( )
( )
∑
∑
−
=
=
=
=
=
−
=
ϕ
−
+
ϕ
=
ϕ
Δ
1
0
0
)
(
)
1
(
)
(
n
i
i
n
i
i
n
f
i
f
i
f
n
n
n
(4.10)
Transformata sumy funkcji dyskretnej
( )
[ ]
( )
( )
( )
[
]
n
f
Z
z
F
gdzie
z
z
F
n
Z
=
−
=
ϕ
1
(4.11)
Splot funkcji dyskretnych i jego transformata
26
Dyskretne Układy Regulacji
Splotem funkcji dyskretnych nazywa się funkcję dyskretną przyjmującą postać

Rozdział 4
( ) ( )
( ) (
)
i
n
f
i
f
n
f
n
f
n
i
−
=
∑
=
2
0
1
2
1
*
(4.12)
Można zauważyć, że odpowiedź układu dynamicznego na ciąg impulsów Diraca z
wagami w postaci wartości sygnału ciągłego (odpowiedź na sygnał impulsowy) jest
splotem funkcji dyskretnych (wzór 2.7). Transformata splotu funkcji dyskretnych
( ) ( )
[
]
( ) (
)
( ) ( )
z
F
z
F
i
n
f
i
f
Z
n
f
n
f
Z
n
i
2
1
2
0
1
2
1
*
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
∑
=
(4.11)
Wynika stąd, że transformata Z odpowiedzi dyskretnej układu y(n) jest określona
wzorem
27
Dyskretne Układy Regulacji
( )
( )
[ ]
( ) (
)
( )
[ ]
( )
[ ]
( ) ( )
z
G
z
U
k
g
Z
k
u
Z
k
n
g
k
u
Z
n
y
Z
z
Y
n
k
k
=
⋅
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
=
∑
=
=0
(4.12)

Rozdział 4
Wielkość G(z) nazywa się transmitancją dyskretną. Jej postać wyprowadza się
zazwyczaj na podstawie równania różnicowego.
Twierdzenia o wartościach granicznych funkcji dyskretnych.
Z transformaty funkcji dyskretnej można uzyskać informacje o jej wartości
początkowej tzn. dla n=0 oraz o wartości dla n
→∞
Wartość początkowa funkcji dyskretnej
( )
( )
( )
( )
z
F
z
z
z
F
n
f
f
z
z
n
1
lim
lim
lim
0
0
−
=
=
=
∞
→
∞
→
→
(4.13)
Wartość końcowa funkcji dyskretnej
( )
( )
( )
z
F
z
z
n
f
f
z
n
1
lim
lim
1
−
=
=
∞
→
∞
→
(4.14)
28
Dyskretne Układy Regulacji
Przykład 4.3

Rozdział 4
Dana jest transformata dyskretnej funkcji wykładniczej
( )
s
T
e
z
z
z
F
α
−
−
=
(4.15)
Należy wyznaczyć wartość początkową i końcową funkcji dyskretnej dla
α>0.
Ze wzoru (4.13) wartość początkowa wykładniczej funkcji dyskretnej
( )
( )
1
lim
lim
0
0
=
−
=
=
α
−
∞
→
→
s
T
z
n
e
z
z
n
f
f
(4.16)
a ze wzoru (4.14) wartość końcowa funkcji dyskretnej
( )
( )
0
1
lim
lim
1
=
−
−
=
=
∞
α
−
→
∞
→
s
T
z
n
e
z
z
z
z
n
f
f
(4.17)
29
Dyskretne Układy Regulacji

Rozdział 4
4.3 Transmitancja dyskretna
Transmitancję wyprowadza się z równania różnicowego zbudowanego z funkcji
przesuniętych
)
(
)
1
(
...
)
(
)
(
)
1
(
...
)
1
(
)
(
0
1
0
1
1
n
u
b
n
u
b
m
n
u
b
n
y
a
n
y
a
k
n
y
a
k
n
y
a
m
k
k
+
+
+
+
+
=
+
+
+
+
−
+
+
+
−
(4.18)
gdzie k
≥m. Inna postać równania
(
)
(
)
∑
∑
=
=
−
=
=
−
−
+
=
−
+
m
j
j
j
m
k
i
i
i
k
j
m
n
u
b
i
k
n
y
a
0
0
(4.19)
Obie strony równania poddaje się transformacji Z przy zerowych warunkach
początkowych, otrzymując przy wykorzystaniu transformat funkcji przesuniętych
30
Dyskretne Układy Regulacji
( )
( )
∑
∑
=
=
−
−
−
=
=
−
=
m
j
j
j
m
j
m
i
k
k
i
i
i
k
z
U
z
b
z
Y
z
a
0
0
(4.20)

Rozdział 4
Stosunek transformaty sygnału wyjściowego do transformaty sygnału wejściowego przy
zerowych warunkach początkowych nosi nazwę transmitancji dyskretnej
( )
( )
( )
0
1
1
1
0
1
1
1
0
0
a
z
a
z
a
z
a
b
z
b
z
b
z
b
z
a
z
b
z
U
z
Y
z
G
k
k
k
k
m
m
m
m
i
k
k
i
i
i
k
m
j
j
j
m
j
m
+
+
+
+
+
+
+
+
=
=
=
−
−
−
−
−
=
=
−
=
=
−
−
∑
∑
L
L
(4.21)
Przykład 4.4
Dane jest równanie różnicowe drugiego rzędu
(
)
(
)
( )
(
)
( )
n
u
b
n
u
b
n
y
a
n
y
a
n
y
a
0
1
0
1
2
1
1
2
+
+
=
+
+
+
+
(4.22)
Wyznaczyć transmitancję dyskretną układu.
31
Dyskretne Układy Regulacji
Przekształcenie Z obu stron równania przy zerowych warunkach początkowych

Rozdział 4
( )
( )
( )
( )
( )
z
U
b
z
zU
b
z
Y
a
z
zY
a
z
Y
z
a
0
1
0
1
2
2
+
=
+
+
(4.23)
Transmitancja dyskretna
( )
( )
( )
0
1
2
2
0
1
a
z
a
z
a
b
z
b
z
U
z
Y
z
G
+
+
+
=
=
(4.24)
Koniec przykładu.
Transformata odpowiedzi układu dyskretnego jest określona wzorem
( ) ( ) ( )
z
U
z
G
z
Y
=
(4.25)
Wyznaczanie funkcji dyskretnej na podstawie transformaty Z
32
Dyskretne Układy Regulacji
Transformata odpowiedzi nie jest wystarczająca do oceny zachowania układu
dyskretnego. Należy zbadać także przebieg funkcji dyskretnej odpowiedzi badanego

Rozdział 4
układu. Stosuje się ogólna metodę znaną jako odwrotne przekształcenie Z. W prostszych
przypadkach można zastosować rozkład funkcji zespolonej Y(z) na szereg potęgowy.
Funkcja zespolona Y(z) jest najczęściej funkcja wymierną zmiennej zespolonej z
( )
( ) ( )
( )
( )
( )
0
1
1
1
c
z
c
z
c
z
c
z
L
z
M
z
L
z
U
z
G
z
Y
l
l
l
l
+
+
+
+
=
=
=
−
−
L
(4.26)
33
Dyskretne Układy Regulacji
W wyrażeniu na Y(z) występuje oprócz transmitancji dyskretnej także transformata
sygnału wejściowego układu. Trzeba zwrócić uwagę na to, że oprócz miejsc zerowych
mianownika transmitancji wystąpią miejsca zerowe transformaty sygnału U(z), co jest
istotne przy wyznaczaniu przebiegu funkcji dyskretnych. Odwrotne przekształcenie Z
wymaga rozwiązania równania charakterystycznego transformaty, to znaczy równania
otrzymanego po przyrównaniu wielomianu mianownika do 0

Rozdział 4
0
0
1
1
1
=
+
+
+
+
−
−
c
z
c
z
c
z
c
l
l
l
l
L
(4.27)
Pierwiastki równania w najprostszym przypadku są pojedyncze
l
z
z
z
z
,
,
,
,
3
2
1
L
(4.28)
Odwrotne przekształcenie Z jest określone wzorem
( )
( )
[
]
1
Re
−
∑
=
n
l
z
z
z
F
s
n
f
l
(4.29)
Res
jest skrótem od residuum - pojęciem z dziedziny funkcji zespolonych. W
przypadku funkcji wymiernej (4.21) dla pierwiastków jednokrotnych składniki sumy mają
postać
34
Dyskretne Układy Regulacji
( )
[
]
( )(
)
[
]
1
1
lim
Re
−
→
−
−
=
n
l
z
z
n
z
z
z
z
z
Y
z
z
Y
s
l
l
(4.30)

Rozdział 4
Dla pierwiastków wielokrotnych składniki sumy przyjmują postać zależną od
wielokrotności pierwiastków równania charakterystycznego
( )
[
]
(
)
( )(
)
[
]
l
l
l
l
l
z
n
m
l
m
m
l
n
z
z
z
z
z
Y
dz
d
m
z
z
Y
s
1
1
1
1
!
1
1
Re
−
−
−
−
−
−
=
(4.31)
gdzie m
l
jest krotnością pierwiastka z
l
.
Przykład 4.4
Wyznaczyć oryginał dyskretny transformaty funkcji dyskretnej
35
Dyskretne Układy Regulacji
( ) (
)(
)
2
.
0
1
.
0
+
−
=
z
z
z
z
Y
(4.32)

Rozdział 4
Miejsca zerowe mianownika to z
1
=0.1 i z
2
=-0.2. Pierwiastki są jednokrotne a zatem
można stosować wzór (4.29) i (4.30).
( )
(
)
(
)(
)
(
)
(
)(
)
( )
(
)
(
)
[
]
n
n
n
n
z
n
z
n
z
z
z
z
z
z
z
z
z
z
n
y
2
.
0
1
.
0
3
.
0
1
2
.
0
3
.
0
2
.
0
1
.
0
3
.
0
1
.
0
2
.
0
1
.
0
2
.
0
2
.
0
1
.
0
1
.
0
1
1
2
.
0
1
1
.
0
1
2
1
−
−
=
−
−
−
+
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
+
+
⎥
⎦
⎤
⎢
⎣
⎡
+
−
−
=
−
−
−
=
−
=
−
(4.33)
36
Dyskretne Układy Regulacji
Można sprawdzić, że wartość początkowa sygnału y(n) wyznaczona ze wzoru (4.33) i
z twierdzenia o wartości początkowej są sobie równe. Wartości początkowe wyznaczono
określając następujące granice:

Rozdział 4
( )
( )
(
)(
)
( )
( )
( ) (
)
[
]
0
2
.
0
1
.
0
3
.
0
1
lim
lim
0
0
2
.
0
1
.
0
lim
lim
0
0
0
=
−
−
=
=
=
+
−
=
=
→
→
∞
→
∞
→
n
n
n
n
z
z
n
y
y
z
z
z
z
Y
y
(4.34)
Koniec przykładu.
Wyznaczanie oryginału transformaty przez rozkład na szereg potęgowy.
Przykład 4.5
Wyznaczyć oryginał dyskretny transformaty funkcji dyskretnej z przykładu 4.4
( ) (
)(
)
2
.
0
1
.
0
2
.
0
1
.
0
2
−
+
=
+
−
=
z
z
z
z
z
z
z
Y
(4.35)
stosując rozwinięcie na szereg potęgowy zmiennej z.
37
Dyskretne Układy Regulacji
Po podzieleniu licznika i mianownika transformaty przez najwyższa potęgę

Rozdział 4
mianownika i po wykonaniu dzielenia wielomianów otrzymano
( )
(
)
L
+
+
−
+
=
−
+
=
−
−
−
−
−
−
3
2
1
2
1
1
21
.
0
1
.
0
0
2
.
0
1
.
0
1
:
z
z
z
z
z
z
z
y
(4.36)
Współczynniki rozwinięcia są kolejnymi wartościami funkcji dyskretnej w chwilach
0,1,2,3...
Koniec przykładu.
Wyznaczanie transmitancji dyskretnej
Transmitancję można wyznaczyć mając do dyspozycji równanie różnicowe w postaci
sumy funkcji przesuniętych jak we wzorach (4.18) – (4.21). Podobna operację można
przeprowadzić mając zapis układu dyskretnego w przestrzeni stanów (3.7),(3.8).
(
)
( )
( )
38
Dyskretne Układy Regulacji
( )
( )
( )
n
Du
n
Cx
n
y
n
Bu
n
Ax
n
x
+
=
+
=
+1
(4.37)

Rozdział 4
Po przekształceniu Z równań otrzymano
( )
( )
( )
( )
( )
( )
z
DU
z
CX
z
Y
z
BU
z
AX
z
zX
+
=
+
=
(4.38)
Przekształcenie równań macierzowych (4.38) prowadzi do następującego wyniku:
[
]
( )
( )
( )
[
]
( )
( )
( )
( )
( )
[
]
( )
( )
( )
[
]
D
B
A
z
C
z
G
z
DU
z
BU
A
z
C
z
Y
z
DU
z
CX
z
Y
z
BU
A
z
z
X
z
BU
z
X
A
z
+
−
=
+
−
=
→
+
=
−
=
→
=
−
−
−
−
1
1
1
1
1
1
1
(4.39)
W ogólnym przypadku sygnały u(n) i y(n) a także ich transformaty są wektorami (MIMO),
a w związku z tym G(z) jest macierzą transmitancji dyskretnych. Poprawny jest wzór
( )
( ) ( )
z
U
z
G
z
Y
=
(4.40)
39
Dyskretne Układy Regulacji
Natomiast nie można wyznaczyć G(z)=Y(z)/U(z). Taka zależność jest poprawna tylko w

Rozdział 4
układach SISO.
Przekształcenie opisu w przestrzeni stanów dyskretnych na transmitancję (macierz
transmitancji) jest operacja jednoznaczną. To znaczy dla danego równania różnicowego
otrzymuje się jedną postać transmitancji (dla części obserwowalnej i sterowalnej).
Przejście od transmitancji dyskretnej do opisu w przestrzeni stanów nie jest jednoznaczne
i wynik zależy od przyjętej metody postępowania. Bardzo często stosuje się tzw. metodę
bezpośrednią. Przebieg postępowania jest następujący. Z transmitancji (4.21) otrzymuje
się
( )
( )
[
]
( )
z
E
z
b
z
b
z
b
z
b
z
U
z
a
z
a
z
a
z
b
z
b
z
b
z
b
z
Y
n
n
n
m
m
n
m
m
n
n
k
n
n
n
m
m
n
m
m
−
+
−
−
−
−
−
−
+
−
−
−
−
+
−
−
−
−
−
+
+
+
+
=
=
+
+
+
+
+
+
+
+
=
0
1
1
1
1
0
1
1
1
1
0
1
1
1
1
1
L
L
L
(4.41)
40
Dyskretne Układy Regulacji
Zmienna pomocnicza E(z) umożliwia wprowadzenie równania sumatora

Rozdział 4
( )
[
]
( )
( )
( )
( )
( )
( )
z
E
z
a
z
E
z
a
z
E
z
a
z
U
z
E
z
E
z
a
z
a
z
a
z
U
n
k
k
n
n
k
−
−
−
−
−
−
+
−
−
−
−
−
−
−
=
+
+
+
+
=
0
2
2
1
1
0
1
1
1
1
1
L
L
(4.42)
41
Dyskretne Układy Regulacji
Równania najlepiej jest zilustrować schematem blokowym, na którym wykorzystano
bloki opóźniające o jeden okres impulsowania z
-1
.
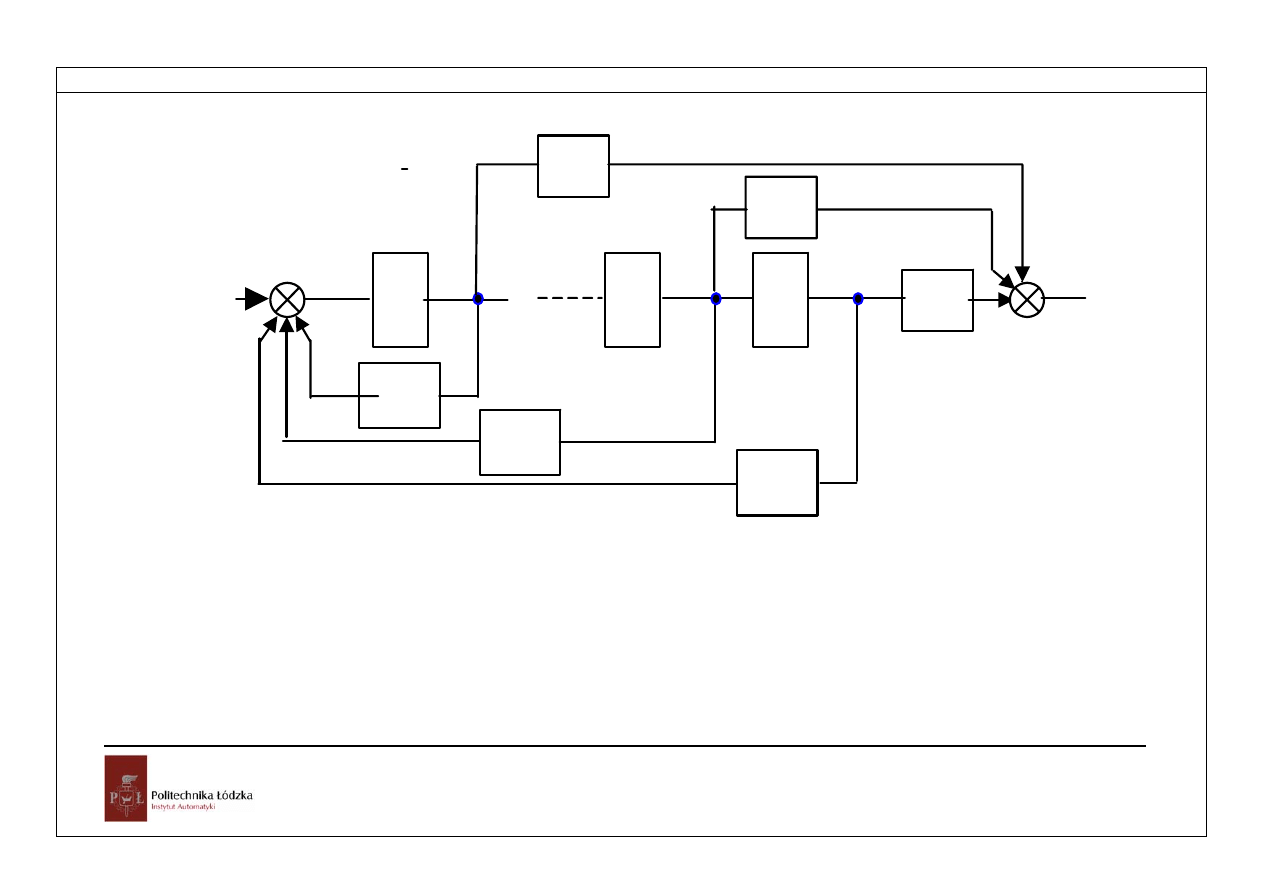
Rozdział 4
y(k)
b
0
z
-1
u(k)
x
n
(k+1)
-a
1
x
n-1
(k)
x
2
(k)
x
1
(k)
-a
n-1
z
-1
z
-1
-a
0
b
n-1
b
1
Rys.4.1.Schemat blokowy układu metodą bezpośrednią
42
Dyskretne Układy Regulacji
Ze schematu wynika równanie

Rozdział 4
(
)
( )
( )
( )
[
]
( )
[ ]
( )
n
u
n
x
b
b
b
n
y
n
u
n
x
a
a
a
a
n
x
n
n
0
1
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
1
0
1
1
1
0
1
2
1
0
+
=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
=
+
−
−
M
L
L
M
M
M
M
L
L
L
(4.43)
43
Dyskretne Układy Regulacji
Oprócz przedstawionej metody bezpośredniej korzysta się z innych standardowych
postaci otrzymanych metoda równoległą, iteracyjną i innymi. Macierze w innych
metodach mają te same wymiary, ale różne elementy. Na przykład w metodzie
równoległej macierz stanu ma postać

Rozdział 4
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
n
z
z
z
A
L
O
L
L
0
0
0
0
0
0
0
0
0
2
1
(4.44)
W macierzy A na przekątnej występują miejsca zerowe wielomianu mianownika
transmitancji. Budowa tej macierzy w przypadku biegunów wielokrotnych jest bardziej
złożona.
Wyznaczanie transmitancji dyskretnej z transmitancji ciągłej obiektu
44
Dyskretne Układy Regulacji
a) Wyznaczanie transmitancji dyskretnej z odpowiedzi impulsowej układu ciągłego
Wiadomo, że odpowiedź układu ciągłego na sygnał impulsowy jest splotem
dyskretnym funkcji dyskretnych wejścia i dyskretnej odpowiedzi impulsowej układu

Rozdział 4
ciągłego. Wynika stąd, że wystarczy wyznaczyć transformatę Z funkcji dyskretnej
odpowiedzi impulsowej układu ciągłego. Rezultat jest transmitancją dyskretną układu.
Przykład 4.6.
Wyznaczanie transmitancji dyskretnej elementu całkującego idealnego, którego
transmitancja ma postać
( )
s
k
s
G
=
(4.45)
gdzie k- współczynnik wzmocnienia.
Odpowiedź impulsowa w postaci dyskretnej będzie wynosiła:
( )
( )
( )
s
nT
k
n
h
t
k
t
h
1
)
(
1
⋅
=
→
⋅
=
(4.46)
45
Dyskretne Układy Regulacji
Transformata Z odpowiedzi ma postać:
Rozdział 4
( )
{ }
( )
{
}
( )
1
1
1
−
=
→
−
=
⋅
=
z
z
z
G
z
z
nT
k
Z
n
h
Z
s
(4.47)
Koniec przykładu 4.6
Przykład 4.7
Element całkujący jak w przykładzie 4.6 jest poprzedzony elementem ZOH
(ekstrapolatorem zerowego rzędu). Należy wyznaczyć transmitancję dyskretną
połączenia.
y(k)
k/s
u(k)
Rys.4.2.Element całkujący poprzedzony ekstrapolatorem zerowego rzędu
46
Dyskretne Układy Regulacji

Rozdział 4
Transmitancja połączenia szeregowego elementów wynosi
( )
2
1
s
e
k
s
G
s
sT
−
−
=
(4.48)
Odpowiedź impulsową i przekształcenie Z zaprezentowano w równaniu (4.49).
( )
( ) (
)
[
]
( )
( ) (
)
[
]
( )
( )
[
]
(
)
(
)
(
)
1
1
1
1
1
)
(
1
1
)
(
1
1
2
2
1
2
−
=
−
−
=
−
−
−
=
=
−
−
−
=
→
−
−
−
=
−
z
kT
z
kzT
z
z
z
kzT
z
z
kzT
nT
h
Z
z
G
T
nT
T
nT
nT
nT
k
nT
h
T
t
T
t
t
t
k
t
h
s
s
s
s
s
s
s
s
s
s
s
s
s
s
(4.49)
Koniec przykładu 4.7
b) Wyznaczanie transmitancji dyskretnej pierwszą metodą Eulera
47
Dyskretne Układy Regulacji
Załóżmy transmitancję członu

Rozdział 4
( )
( )
( )
s
s
E
s
F
s
G
c
1
=
=
(4.50)
Odpowiada to równaniu różniczkowemu
( )
t
e
dt
df =
(4.51)
Całując obie strony równania, otrzymuje się
( )
( )
( )
0
0
0
t
t
dt
t
e
t
f
t
f
t
t
≥
+
=
∫
(4.52)
Dla okresu próbkowania T
s
otrzymuje się
(
)
( )
( )
(
)
dt
t
e
kT
f
T
kT
f
s
s
T
k
kT
s
s
s
∫
+
+
=
+
1
(4.52)
48
Dyskretne Układy Regulacji
Wartość całki można wyznaczyć jako pole prostokąta, jak na rysunku
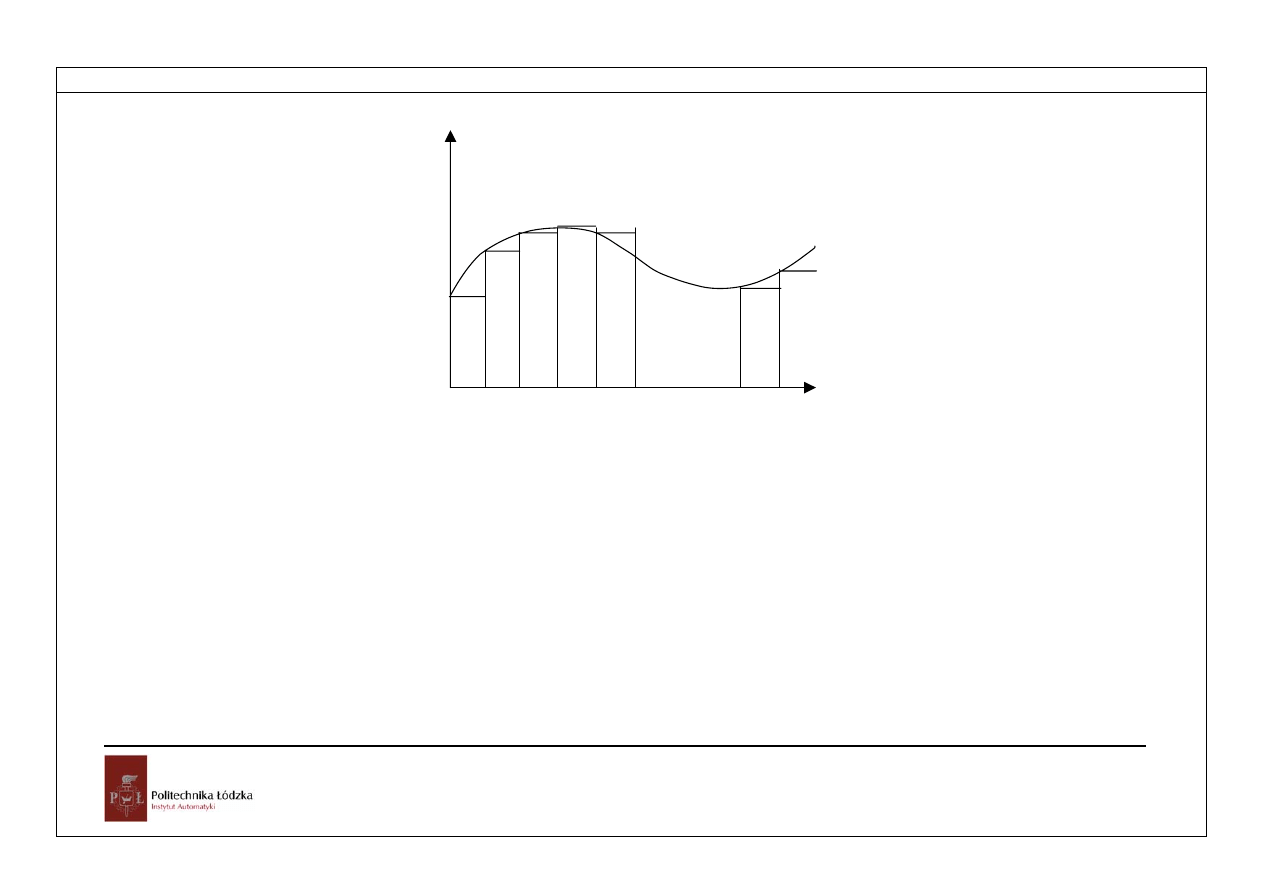
Rozdział 4
kT
s
(k+1)T
s
e(t)
e(kT
s
)
Rys.4.3. Aproksymacja przebiegu ciągłego pierwszą metodą prostokątów
Z rysunku 4.3 wynika wartość całki jako pole prostokąta o podstawie T
s
(
)
( )
( )
s
s
s
s
s
kT
e
T
kT
f
T
kT
f
+
=
+
(4.53)
Z tego równania różnicowego po transformacji Z powstaje równanie
( ) ( )
( )
z
E
T
z
F
z
zF
s
=
−
(4.54)
49
Dyskretne Układy Regulacji
a następnie transmitancja członu całkującego

Rozdział 4
( )
( )
( )
1
−
=
=
z
T
z
E
z
F
z
H
s
(4.55)
Pierwsza metoda Eulera (prostokątów I) może posłużyć do zamiany transmitancji
ciągłej na dyskretną przez podstawienie pokazane we wzorze
( )
( )
1
1
1
1
−
=
=
=
−
=
−
=
z
T
s
s
G
z
H
s
T
z
s
T
z
s
c
s
s
(4.56)
c) Wyznaczanie transmitancji dyskretnej drugą metodą Eulera
Pole prostokąta podczas całkowania może być obliczone tak, jak pokazano to na
rysunku 4.4. Pole prostokąta jest określone jako pole prostokąta o podstawie T
s
i
wysokości e(kT
s
+T
s
).
50
Dyskretne Układy Regulacji
(
)
( )
(
)
s
s
s
s
s
s
T
kT
e
T
kT
f
T
kT
f
+
+
=
+
(4.57)
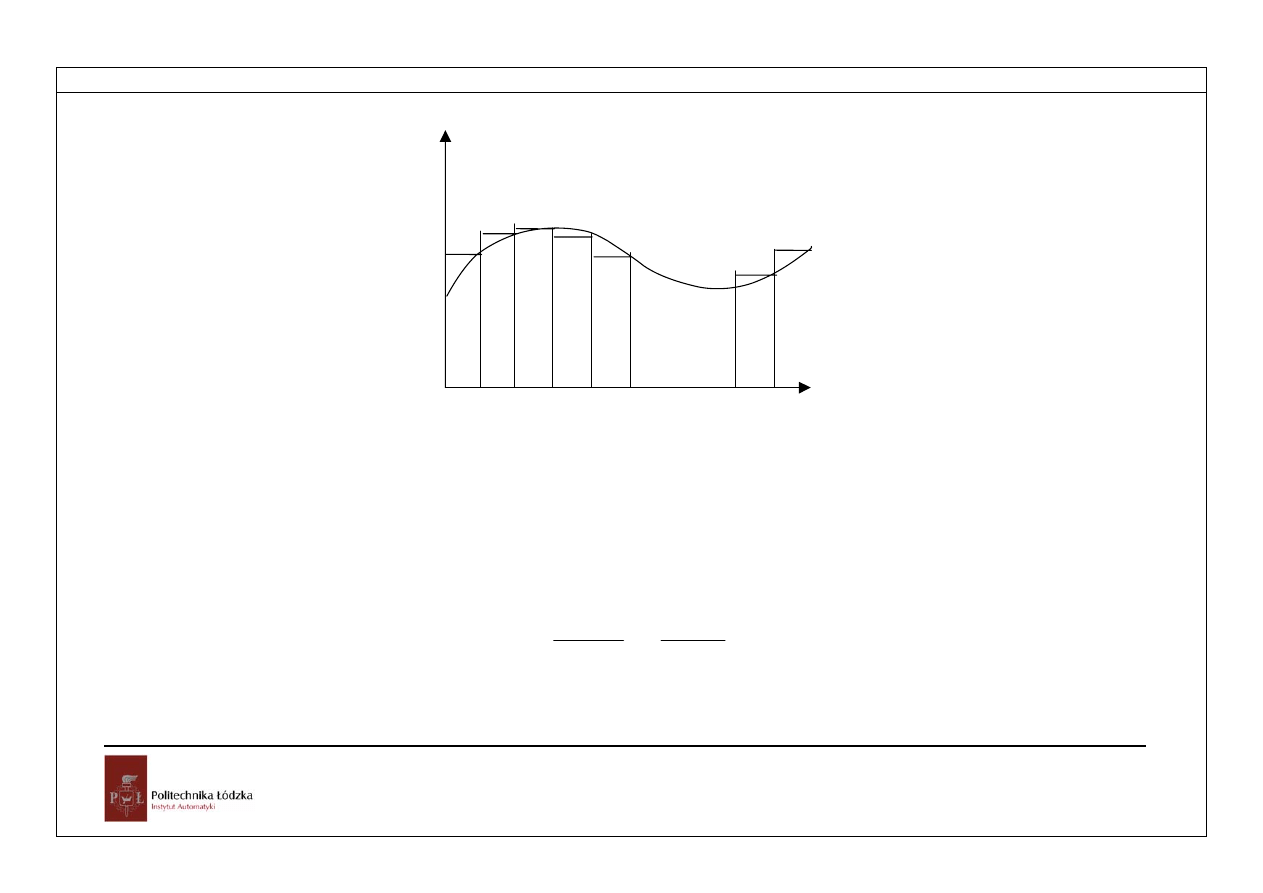
Rozdział 4
(k+1)T
s
kT
s
e(t)
e(k+1)T
s
Rys.4.4. Aproksymacja przebiegu ciągłego drugą metodą prostokątów
Z tego równania różnicowego po transformacji Z otrzymuje się
( ) ( )
( )
z
E
zT
z
F
z
zF
s
=
−
(4.58)
a następnie transmitancję członu całkującego
51
Dyskretne Układy Regulacji
( )
( )
( )
1
−
=
=
z
zT
z
E
z
F
z
H
s
(4.59)

Rozdział 4
Druga metoda Eulera (prostokątów II) może posłużyć do zamiany transmitancji ciągłej
na dyskretną przez podstawienie pokazane we wzorze
( )
( )
1
1
1
1
−
=
=
=
−
=
−
=
z
zT
s
s
G
z
H
s
zT
z
s
zT
z
s
c
s
s
(4.60)
d) Wyznaczanie transmitancji dyskretnej metodą Tustina
52
Dyskretne Układy Regulacji
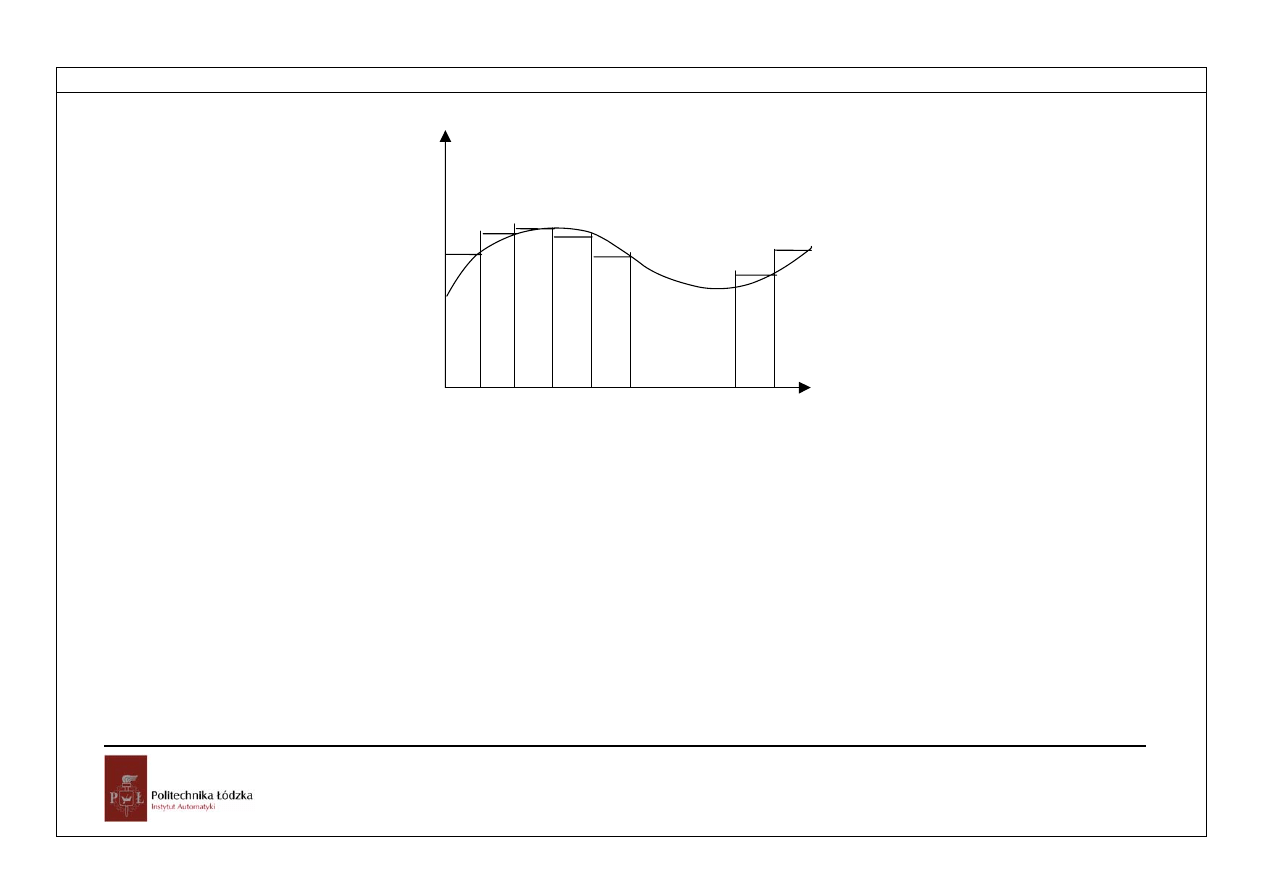
Jest to metoda trapezów, która daje zdecydowanie najlepsze odwzorowania w
porównaniu z metodami prostokątów.
Rozdział 4
(k+1)T
s
kT
s
e(t)
e(k+1)T
s
Rys.4.4. Aproksymacja przebiegu ciągłego drugą metodą prostokątów
53
Dyskretne Układy Regulacji
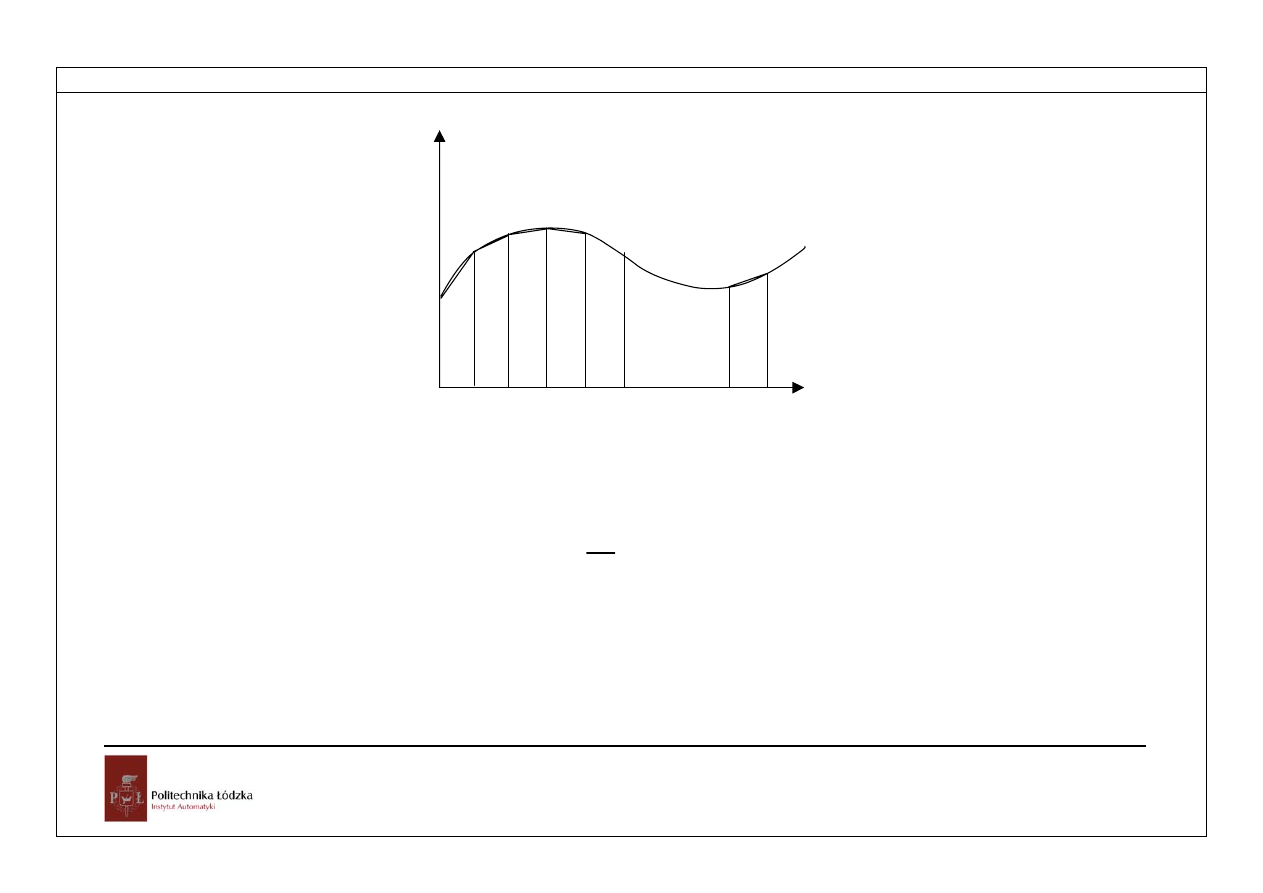
Rozdział 4
kT
s
(k+1)T
s
e(t)
e(kT
s
)
e[(k+1)T
s
]
Rys.4.5. Aproksymacja przebiegu ciągłego metodą trapezów
Z rysunku 4.5 wynika wartość całki jako pole trapezu o wysokości T
s
(
)
( )
( ) (
)
[
]
i
i
i
i
i
i
i
T
kT
e
kT
e
T
kT
f
T
kT
f
+
+
+
=
+
2
(4.61)
54
Dyskretne Układy Regulacji
Z tego równania różnicowego po transformacji Z otrzymuje się

Rozdział 4
( ) ( )
( )
( )
[
]
z
zE
z
E
T
z
F
z
zF
s
+
=
−
2
(4.62)
a następnie transmitancję członu całkującego
( )
( )
( )
1
1
2
−
+
=
=
z
z
T
z
E
z
F
z
H
s
(4.63)
Metoda Tustina (metoda trapezów) może posłużyć do zamiany transmitancji ciągłej na
dyskretną przez podstawienie pokazane we wzorze dla członu całkującego (4.63):
( )
( )
1
1
2
1
1
1
2
1
1
2
−
+
=
=
=
+
−
=
+
−
=
z
z
T
s
s
G
z
H
s
z
z
T
s
z
z
T
s
c
s
s
(4.64)
Przykład 4.8
55
Dyskretne Układy Regulacji
Wyznaczyć różnymi metodami transmitancje dyskretne elementu inercyjnego

Rozdział 4
pierwszego rzędu, którego transmitancję ciągłą określono wzorem
( )
1
+
=
sT
k
s
G
(4.65)
gdzie k – współczynnik proporcjonalności, T – stała czasowa.
Założono, że element inercyjny jest poprzedzony ekstrapolatorem zerowego rzędu.
a) Metoda odpowiedzi impulsowej
( )
1
1
+
−
=
−
sT
k
s
e
s
g
s
sT
(4.67)
56
Dyskretne Układy Regulacji
Postać funkcji dyskretnej

Rozdział 4
( )
( )
(
) ( )
(
)
( )
( )
( )
( )
( )
( )
s
s
s
s
T
t
T
T
t
T
t
nT
g
nT
g
nT
g
t
g
t
g
t
g
T
t
e
k
t
e
k
t
g
s
s
2
1
2
1
1
1
1
1
1
−
=
→
−
=
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
−
−
−
−
−
(4.66)
Transformata funkcji dyskretnej
( )
( )
{
}
( )
( )
{
}
( )
{
}
( )
{
}
s
s
s
s
s
nT
g
Z
z
nT
g
Z
nT
g
nT
g
Z
nT
g
Z
z
G
1
1
1
2
1
−
−
=
=
−
=
=
(4.67)
57
Dyskretne Układy Regulacji
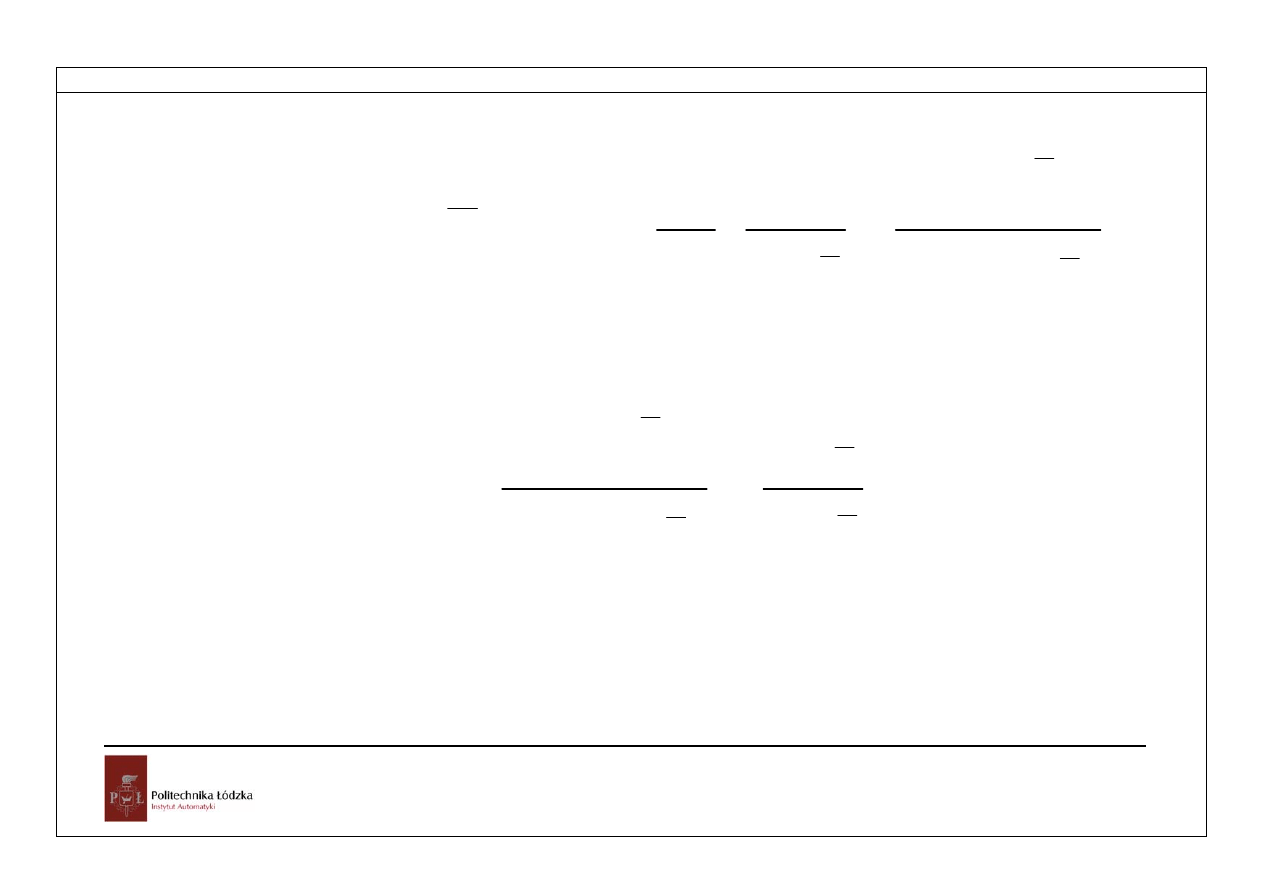
Rozdział 4
( )
{
}
( )
( )
(
)
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
−
−
−
=
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
−
−
−
−
T
T
T
T
T
T
s
T
nT
s
s
s
s
s
s
e
z
z
e
kz
e
z
z
z
z
k
nT
e
nT
k
Z
nT
g
Z
1
1
1
1
1
1
(4.68)
Po uwzględnieniu wzoru (4.67) otrzymuje się transmitancję elementu inercyjnego
( )
(
)
(
)
T
T
T
T
T
T
T
T
s
s
s
s
e
z
e
k
e
z
z
e
kz
z
z
G
−
−
−
−
−
−
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
=
1
1
1
1
1
(4.69)
b) Transmitancja dyskretna z równania stanu elementu inercyjnego
58
Dyskretne Układy Regulacji
Macierze elementu inercyjnego z równania (3.27)
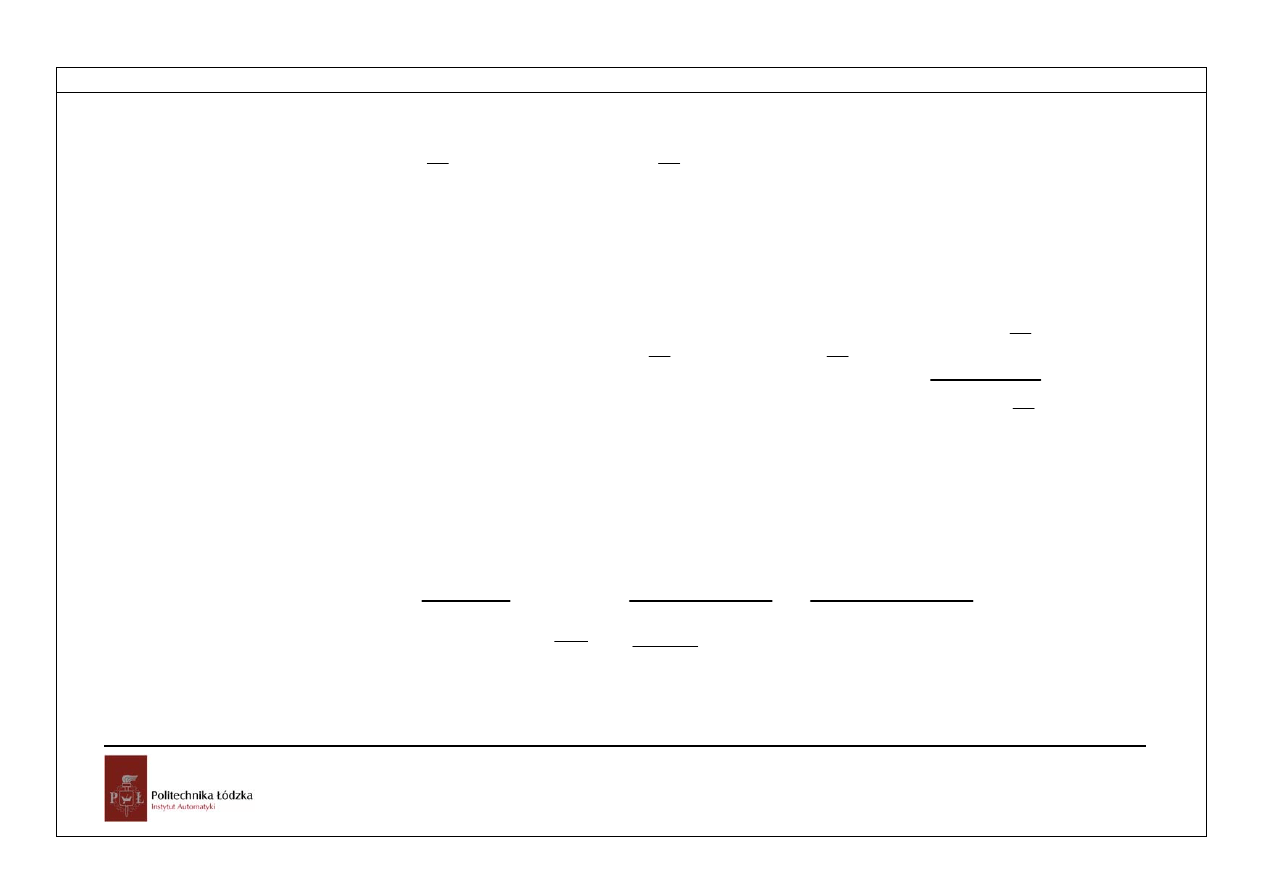
Rozdział 4
0
1
1
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
=
−
−
D
C
e
k
B
e
A
T
T
T
T
s
s
(4.70)
Transmitancja dyskretna z (4.39)
( )
[
]
T
T
T
T
T
T
T
T
s
s
s
s
e
z
e
k
e
k
e
z
D
B
A
z
C
z
G
−
−
−
−
−
−
−
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
⎥
⎦
⎤
⎢
⎣
⎡
−
=
+
−
=
1
1
1
1
1
(4.71)
Wynik jest analogiczny jak w poprzednio w punkcie a).
c) Transmitancja I metodą Eulera (metoda prostokątów)
59
Dyskretne Układy Regulacji
( )
( )
T
T
zT
kT
T
T
z
k
sT
k
s
G
z
G
s
s
s
T
z
s
s
−
+
=
+
−
=
⎭
⎬
⎫
⎩
⎨
⎧
+
=
=
−
=
1
1
1
1
(4.72)

Rozdział 4
Wynik ten jest uproszczonym wyrażeniem (4.71). Rozwinięcie w szereg Maclaurina
funkcji wykładniczej i pozostawienie liniowych składników rozwinięcia
T
T
T
T
T
T
T
T
e
s
s
s
s
T
T
s
−
≅
+
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
−
1
!
3
1
!
2
1
1
3
2
L
(4.73)
we wzorze na transmitancję (4.71) prowadzi do wyniku otrzymanego metodą prostokątów
(4.72)
60
Dyskretne Układy Regulacji
( )
T
T
zT
kT
T
T
z
T
T
k
e
z
e
k
z
G
s
s
s
s
T
T
T
T
s
s
−
+
=
+
−
+
−
≅
−
−
=
−
−
1
1
1
1
(4.74)

Literatura
Literatura
[1] Ackerman J.: Regulacja impulsowa. WNT, Warszawa 1976
[2] Brzózka J.: Regulatory cyfrowe w automatyce. Mikom, Warszawa2002
[3] Brzózka J.: Regulatory i układy automatyki. Mikom, Warszawa2004
[4] Dębowski A.: Automatyka. Podstawy teorii. WNT, Warszawa 2008
[5] Gessing R.: Teoria sterowania. Część I. Układy liniowe. Skrypt uczelniany ' Politechniki Śląskiej nr 1302,
Gliwice 1987.
[6] Kaczorek T.: Teoria sterowania. T.1. PWN, Warszawa 1977
[7] Kaczorek T.: Teoria układów regulacji automatycznej. WNT, Warszawa 1977
[8] Laboratorium Teorii Sterowania i Podstaw Automatyki, Błachuta M. [red.]: (praca zbiorowa), Wydawnictwo
Politechniki Śląskiej nr 2082
[9] Markowski A., Kostro J., Lewandowski A.: Automatyka w pytaniach i odpowiedziach. WNT, Warszawa 1979
[10] Markowski J.: Elementy urządzenia i układy automatyki. WSiP, Warszawa 2006
[11] Mutambara A.: Design and Analysis of Control Systems. CRC Press, New York, 1999
[12] Niederliński A.: Systemy i sterowanie. Wyd. Politechniki Śląskiej, skrypt Nr 746, Gliwice 1978
[13] Ogata K.: Discrete – time control systems. Prentice Hall Inter., Englewood Cliffs 1987
[14] PN-88 M-42000 Automatyka i pomiary przemysłowe. Terminologia
[15] Rumatowski K.: podstawy automatyki. Część 2. Układy dyskretne i stochastyczne. Wydawnictwo Politechniki
Poznańskiej, Poznań 2005
[16] Schönfeld R.: Digitale Regelung elektrischer Abtriebe. VEB Verlag, Berlin 1987
61
Dyskretne Układy Regulacji
[17] Schönfeld R.: Grundlagen der automatischen Steuerung. VEB Verlag, Berlin 1984

Literatura
[18] Sinha N.K.: Controls systems. John Wiley &Sons, New York 1995
[19] Takahashi Y., Rabins M., Auslander D.: Sterowanie i systemy dynamiczne. WNT, Warszawa 1976
[20] Tewari A.: Modern Control Design with Matlab and Simulink. John Wiley & Sons Ltd, New York 2002
[21] Wajs K.: Linie pierwiastkowe w automatyce. WNT, Warszawa 1973
[22] http://pl.wikipedia.org/wiki/SCADA
[23] http://pl.wikipedia.org/wiki/System_czasu_rzeczywistego
62
Dyskretne Układy Regulacji
Document Outline
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron