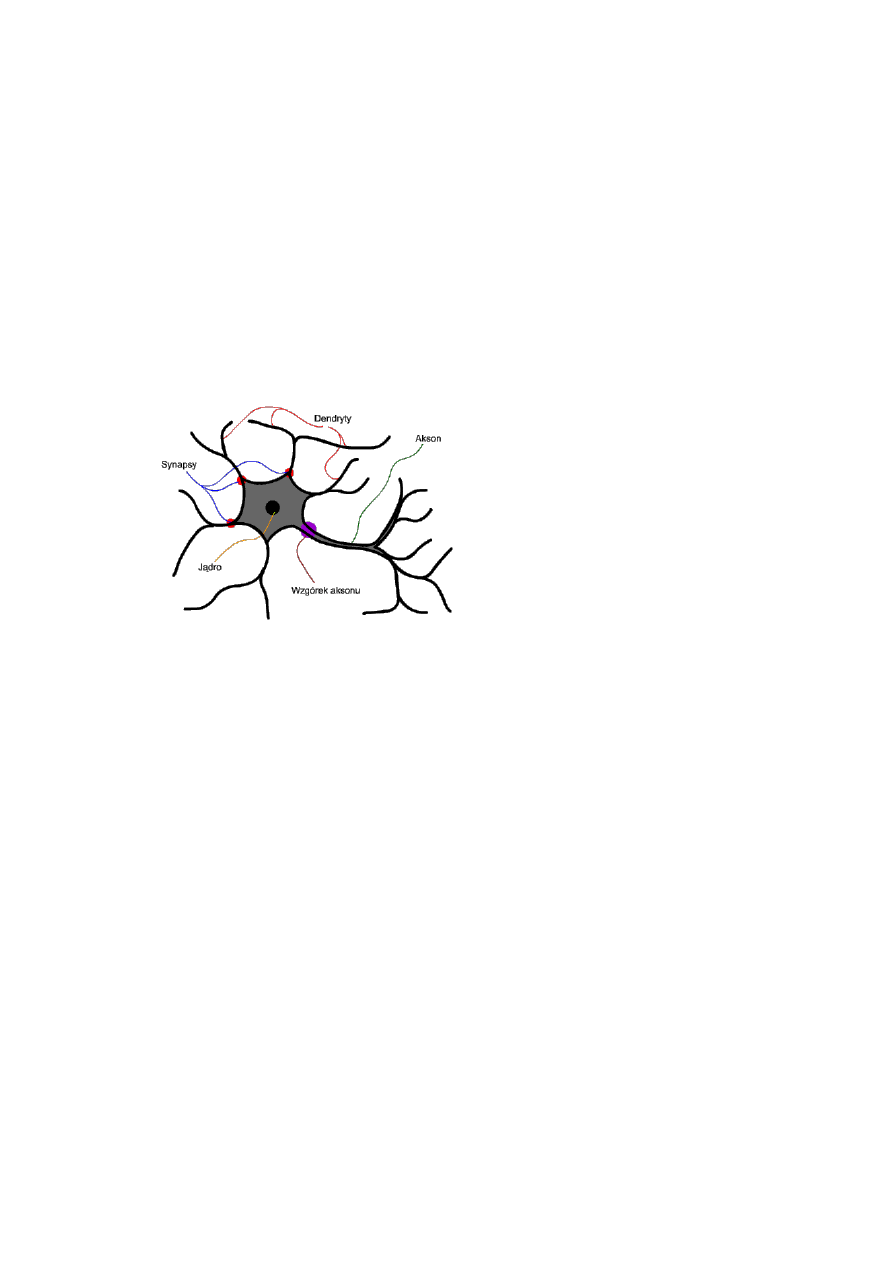
Model pojedynczego neuronu.

1.

Sieć neuronowa –

jest to system symulujący pracę mózgu. Mózg składa się z

komórek nerwowych zwanych neuronami. Pomiędzy nimi znajdują się cieniutkie
połączenia - tzw.

aksony

. W powiększeniu fragment mózgu wygląda jak drobna sieć,

której węzłami są neurony. Sieć neuronowa służy do wszelkiego rodzaju
rozpoznawania, kojarzenia, przewidywania, sterowania.

2.

Budowa sieci neuronowej –

sieć neuronowa składa się z neuronów. Neuron

to w oryginale - komórka nerwowa. W sieci neuronowej - podstawowy jej składnik.



Jądro -

"centrum obliczeniowe" neuronu. To tutaj zachodzą procesy kluczowe dla

funkcjonowania neuronu.



Akson -

"wyjście" neuronu. Za jego pośrednictwem neuron powiadamia świat

zewnętrzny o swojej reakcji na dane wejściowe. Neuron ma tylko jeden akson.



Wzgórek aksonu

- stąd wysyłany jest sygnał wyjściowy, który wędruje dalej

poprzez akson.



Dendryt -

"wejście" neuronu. Tędy trafiają do jądra sygnały mające być w nim

później poddane obróbce. Dendrytów może być wiele - biologiczne neurony mają ich
tysiące.



Synapsa -

jeśli dendryt jest wejściem neuronu, to synapsa jest jego furtką. Może ona

zmienić moc sygnału napływającego poprzez dendryt.

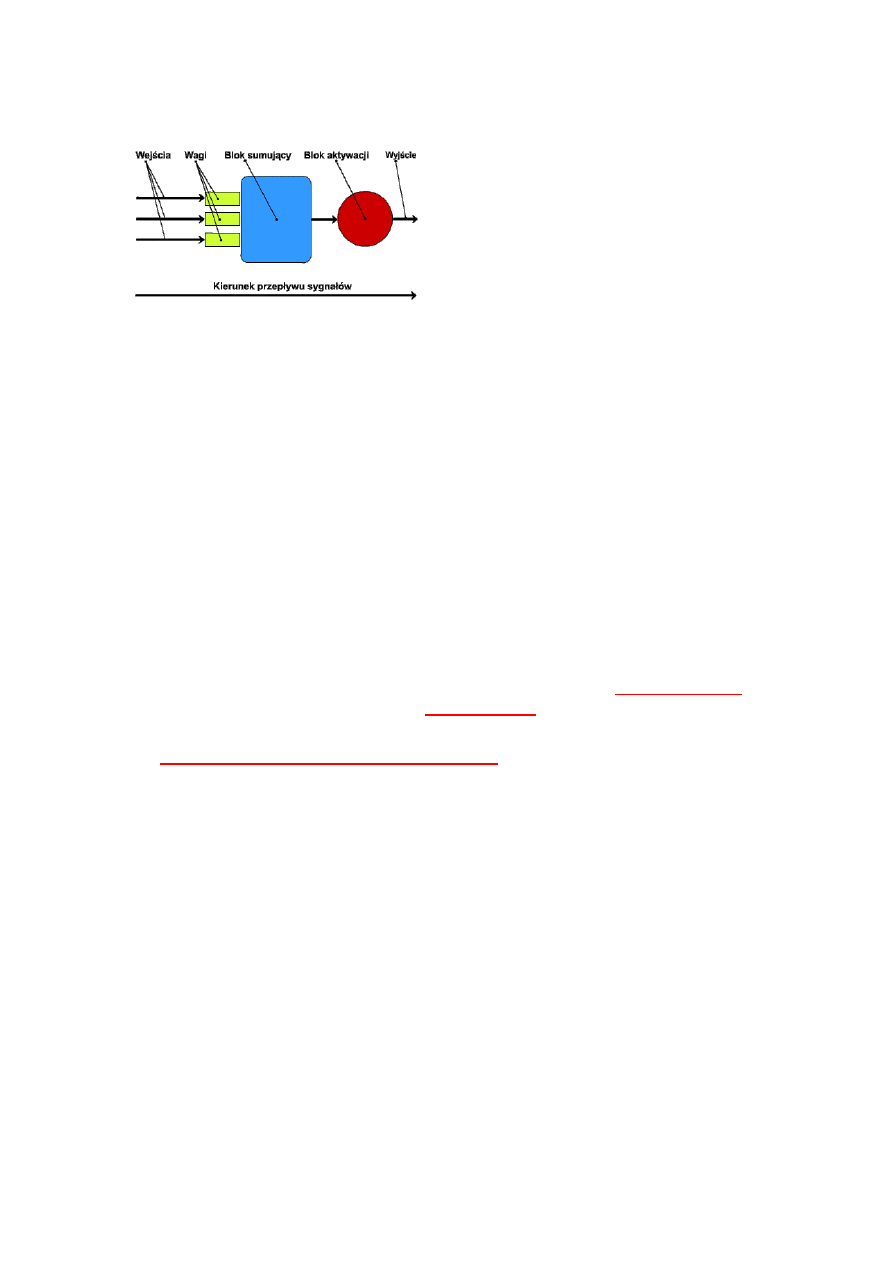
Model neuronu składa

się z dokładnie tych samych elementów, które wyżej wymieniono.

Wejścia

to dendryty, lub ściślej: sygnały przez nie nadchodzące- sygnały wejściowe.

Sygnał wejściowy

- sygnał trafiający na wejście neuronu (sieci).

Wagi

to cyfrowe odpowiedniki modyfikacji dokonywanych na sygnałach przez synapsy.

Waga to wartość, przez którą mnoży się odpowiedni sygnał wejściowy neuronu.

Blok sumujący

to odpowiednik jądra. Część neuronu, w której obliczana jest suma jego

ważonych wejść.

Blok aktywacji

to wzgórek aksonu. Część neuronu, w której potencjał membranowy jest

przekształcany w sygnał wyjściowy za pomocą funkcji aktywacji.

Funkcja aktywacji -

funkcja, według której potencjał membranowy neuronu jest

przekształcany w jego sygnał wyjściowy.

Wyjście

- to akson.

Sygnał wyjściowy

- sygnał wychodzący z bloku aktywacji neuronu. Wyjście sieci -

połączone wyjścia neuronów ostatniej warstwy wyjściowej.

3. Rodzaje struktur sieci

(na wykładach był tylko MODEL

Wielowarstwowej sieci

jednokierunkowej –

on tylko obowiązuje na zaliczenie )



Jednowarstwowe sieci jednokierunkowe –

sieć jednowarstwowa jest bardziej złożoną strukturą niż pojedynczy neuron. Złożoność ta
skutkuje większą możliwością realizacji zadań. Wśród jednowarstwowych sieci
jednokierunkowych wyróżnia się sieci o liniowej i nieliniowej funkcji aktywacji. Te drugie
nazywamy preceptorami.

Perceptron

- sieć jednokierunkowa złożona z neuronów o

nieliniowej (unipolarnej lub bipolarnej) funkcji aktywacji, sygnał przebiega w jednym
kierunku od wejścia sieci do jej wyjścia.

Struktura jednowarst. sieci jednok. –

Składa się z pojedynczych neuronów,

tworzących warstwę. Każdy z neuronów jest identyczny (ten sam model). Sieć nie zawiera
żadnych dodatkowych połączeń między neuronami oraz między wejściami neuronów a ich
wyjściami.

Uczenie jednowarst. sieci jednok.

– Ideą uczenia sieci jest prezentowanie (podawanie

na wejście sieci) kolejnych elementów ciągu uczącego i porównywanie odpowiedzi sieci z
oczekiwanym stanem na jej wyjściu.

Ciąg uczący

jest zbiorem par uczących.

Para ucząca

– składa się z sygnału (obrazu) i oczekiwanej odpowiedzi sieci.

Uczenie warstwy neuronów

polega na zmianie wartości wag macierzy. Następnie uogólniamy

ten algorytm dla neuronów o funkcji nieliniowej. Algorytm ten, który jest

algorytmem

iteracyjnym

, nazwany został

regułą delta

. Do realizacji algorytmu niezbędny jest ciąg

uczący, zaliczany do grupy

algorytmów uczenia z nauczycielem

. Punktem wyjścia algorytmu

jest wyznaczenie wartości sumarycznego błędu na wyjściu sieci.

Problem uczenia sieci

można określić jako problem minimalizacji błędu, do której można

wykorzystać np.

gradientową metodę największego spadku

.



Wielowarstwowe sieci jednokierunkowe.

Sieć wielowarstwowa jest najbardziej złożoną strukturą sieci jednokierunkowych.

Omówiono na podstawie perceptronu wielowarstwowego.

Struktura perceptronu wielowarstwowego.

Dodanie do opisanych powyżej struktury sieci kolejnych warstw spowoduje utworzenie sieci
wielowarstwowej – perceptronu wielowarstwowego.

Perceptron wielowarstwowy –

jednokierunkowa sieć wielowarstwowa o nieliniowej

funkcji aktywacji.
Kolejne warstwy mogą być połączone ze sobą na zasadzie „każdy z każdym” – dotyczy to
jednak warstw ze sobą bezpośrednio sąsiadujących. Warstwa pierwsza jest nazywana

warstwą

wejściową

, a ostatnia

wyjściową

. Jeżeli sieć ma więcej niż dwie warstwy, to wszystkie oprócz

pierwszej i ostatniej, nazywane są

ukrytymi

. Sieć składa się z identycznych neuronów o

nieliniowej aktywacji w postaci funkcji logistycznej.
Uczenie perceptronu wielowarstwowego – algorytm zamiany wartości wag oraz ciąg uczący
jest analogiczny dla perceptronu prostego. Jednym istotnym problemem jest wyznaczenie
błędu sieci na wyjściach warstwy wejściowej i warstw ukrytych (wartości żądane dla tych
warstw nie są zawsze w ciągu uczącym). Dla tych warstw brak jest w ciągu uczącym
informacji o żądanej wartości „z”. Problem ten można rozwiązać stosując algorytm wstecznej
propagacji, który jest jednym z najbardziej skutecznych algorytmów wykorzystywanych do
uczenia jednokierunkowych sieci wielowarstwowych.

Idea tego algorytmu:

1. Na wejście sieci wprowadzamy pierwszy wektor X z ciągu uczącego.
2. Wyznaczamy wartość wektora wyjściowego sieci korzystając z zależności.
3. Dla każdego neuronu warstwy wyjściowej wyznaczmy wartość błędu.
4. Wyznaczamy wartość błędów dla neuronów warstwy M-1. Gdzie zależność ta, jest to

suma wszystkich błędów warstwy M-tej pomnożona przez te wagi warstwy M-tej,
które łączą dany neuron warstwy M-tej z neuronem k-tym warstwy M-1, dla którego
wyznaczany jest błąd.

5. Wyznacz wartość poprawki dla każdej z wag warstwy M-1-szej
6. Przejść do warstwy M-2 i powtarzać czynności 5 i 6 do momentu wprowadzenia

modyfikacji dla wszystkich wag sieci.

7. Z ciągu uczącego pobrać kolejny wektor X i przejść do czynności 2.

Czynności 1-8 należy powtarzać dla całego ciągu uczącego. Po prezentacji całego

ciągu (epoka uczenia) należy wyznaczyć sumaryczny błąd sieci (np. jako sumę
wszystkich błędów dla całego ciągu uczącego). Jeżeli wartość wyznaczonego błędu jest
większa od przyjętej wartości, to należy ponownie zaprezentować cały ciąg uczenia
zgodnie z podanym algorytmem wstecznej propagacji. Warunkiem zakończenia procesu
uczenia jest 100% poprawności rozwiązania ciągu uczącego lub osiągnięcie ustalonego
poziomu błędnych rozpoznań.

Powyższy sposób wyznaczenia wartości błędu dla warstw ukrytych i warstwy

wejściowej nazywany jest

wsteczną propagacją błędu (ang. Backpropagation –

BP)

, w związku z tym, że algorytm wstecznej propagacji ściśle wiąże się z uczeniem

perceptronu wielowarstwowego (jednok. sieci wielowarstw.), często zamiennie używa się
nazwy: sieć ze wsteczną propagacją błędu. Wartości początkowe wag ustala się jako
wartości losowe o małych wartościach, najczęściej z przedziału (0,0;0,1). Taki sposób
inicjowania wag jest konsekwencją stosowania iteracyjnego algorytmu przyrostowego, w
trakcie, którego wartości wag będą się zwiększały.

4. Sposób działania sieci neuronowej

Generalnie sieci używa się na zasadzie: pokażmy jej coś i zobaczmy, jak zareaguje.

Czyli w skrócie: pytanie - odpowiedź. Owo pytanie to odpowiednio przetworzone dane (np.
obraz, dźwięk, dane giełdowe, warunki pogodowe) przesyłane na wejście sieci. Po
"usłyszeniu" pytania sieć podaje odpowiedź - znów są to pewne dane, które projektant sieci
potrafi przełożyć na konkretne informacje. Najprostszy schemat działania sieci:

Przykład działania sieci neuronowej.

Zasadę działania SSN omówiono na przykładzie jej najmniejszego funkcjonalnego

fragmentu, jakim jest neuron. Samotny neuron to również "pełnoprawna" sieć.

Jak działa neuron?

Ilość wejść zależy od specyfiki zadania. Na wejścia trafiają

sygnały wejściowe

. Są

to po prostu liczby opisujące zadanie, które neuron ma rozwiązać. Każda z

wag

posiada

pewną wartość. Sygnały są mnożone przez wartości wag (czyli ważone), wyniki owego
mnożenia dodawane są do siebie w

bloku sumującym

. W ten sposób powstaje konkretna

liczba, którą określa się jako

potencjał membranowy

. Jest ona wysyłana do

bloku

aktywacji

, gdzie może zostać dodatkowo przetworzona. Po ewentualnej operacji wykonanej

w bloku aktywacji otrzymujemy gotową odpowiedź neuronu na sygnały wejściowe. Oto
przykład z pominięciem bloku aktywacji (za odpowiedź neuronu uznajemy potencjał
membranowy):

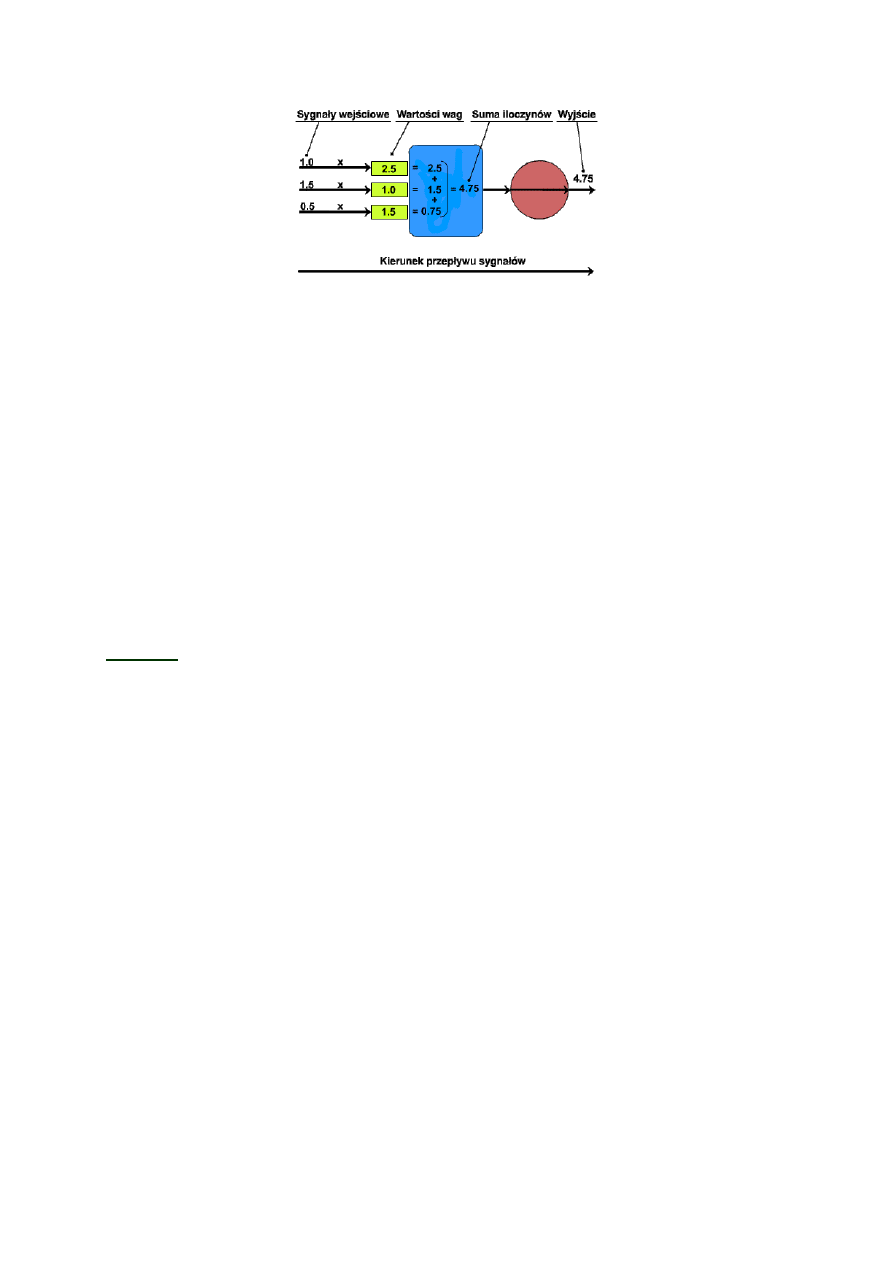
Bloku aktywacji -

jest on pewną funkcją, której argumentem jest potencjał membranowy.

Innymi słowy: jeśli potencjał membranowy oznaczymy jako



, odpowiedź, czyli wyjście

neuronu jako y, a

funkcję aktywacji

jako f, to operację wykonywaną w bloku aktywacji

można zapisać:

y = f (



)

Odpowiedź neuronu zależy więc od tego, jaką funkcją jest f. W powyższym przykładzie
pominęliśmy zupełnie blok aktywacji, jako że przyjęto, iż funkcja aktywacji będzie funkcją
liniową postaci:

f (x) = x

inaczej:

f (



) =



Zatem wartość owej funkcji, czyli odpowiedź neuronu (f (



)), będzie miała zawsze tę samą

wartość, co potencjał membranowy (



). Neuron z taką funkcją aktywacji nazywany jest

neuronem liniowym.

WAGI.

Każde z wejść ma swoją wagę, czyli informację o tym, jak duże znaczenie dla neuronu

ma sygnał podany na to wejście. I tak:

wartość wagi mała

co do wartości bezwzględnej

znaczy, że dane wejście jest niezbyt ważne dla neuronu.

Duża wartość dodatnia

oznacza, że

dane wejście ma duże znaczenie "pozytywne", zaś

duża co do wartości bezwzględnej wartość

ujemna

to znak, iż wejście ma duże znaczenie "negatywne".

W sieciach mianowicie na opisanie dwóch przeciwstawnych stanów używa się liczb
przeciwnych. Zatem nie 1 i 0, a 1 i -1. Wynika to z faktu, iż w SSN zero jest sygnałem
"pustym", nie niosącym żadnej informacji. Przemnóż zerowy sygnał przez dowolną wagę:
wynikiem jest zero. Reasumując: 1 oznacza "tak", -1 - "nie", a 0 - "nieważne".

To, co neuron "wie", zapisane jest w wagach jego wejść. Podobnie jest w przypadku
bardziej skomplikowanej sieci - cała jej wiedza mieści się właśnie w wagach. Nie można przy
tym wyodrębnić z owej bazy wiedzy żadnej konkretnej informacji, czy fragmentu sieci
odpowiadającego za konkretne zadanie - sieć działa wyłącznie jako całość. Podobnie jest w
przypadku ludzkiego mózgu. Wszystko co wiemy, myśli pragnienia, wspomnienia - wszystko
jest "zapisane" w połączeniach synaptycznych. Jeśli z jakichś informacji długo nie
korzystamy, możemy je zapomnieć - nieużywane połączenia synaptyczne mogą zanikać
podobnie, jak nieużywane narządy. W SSN przerwanemu połączeniu odpowiada wejście
neuronu z wagą równą 0. Jakikolwiek sygnał, który trafi na wejście, będzie miał po
przemnożeniu przez tą wagę zerową wartość i zerowe znaczenie dla wartości wyjścia
neuronu.

Modele sieci zawierające sprzężenie zwrotne

( w części praktycznej będą dodatkowo
zadanka z tych właśnie sieci, można mieć
materiały w tej części)



Sieć Hopfielda

BUDOWA.

Sieć Hopfielda jest siecią jednowarstwową zawierającą sprzężenie zwrotne. Sieć ma

identyczną liczbę wejść i wyjść. Na wejście podstawiane są wektory:

X = (x1, x2, .., xi,..,xn), xi {-1,1}
Przy czym wektor wyjściowy ma postać:
Y = (y1, y2,.., yi, …, yn), yi {-1,1}

Każdy z neuronów ma zwrotne połączenie z wejściami z wejściami pozostałych

neutronów. Wyjście pierwszego neuronu jest połączone z pierwszą wagą drugiego neuronu
(bez połączenia z samym sobą), pierwszą wagą trzeciego neuronu i td. Wyjście drugiego
neuronu jest połączone z drugą wagą pierwszego neuronu (bez połączenia z samym sobą),
drugą wagą trzeciego neuronu i td.

FUNKCJONOWANIE.

Sygnał wejściowy (wektor X) podany jest poprzez wolne wagi (te wagi, które nie są

używane w sprzężeniu zwrotnym), a następnie ustala się wartość wyjściową przez funkcję
aktywacji f w postaci

f(e

i

) = {1 gdy (e

i

) >= 0, -1 w przeciwnym wypadku

(e

i

) – suma iloczynu k-tej wagi i-tego neuronu oraz k-tego elementu wektora

wejściowego.

Po wyznaczeniu pierwszego wektora wyjściowego Y, wprowadzony na wejście wektor X

jest odłączany i nie uczestniczy w dalszym przetwarzaniu. W kolejnych krokach wartości
elementów wektora wyjściowego określana jest na podstawie zależności:

Y

i

(t+1) = f(e

i

’)

W trakcie iterowania sygnałów sieci, na jej wyjściu pojawiają się kolejne wektory

wyjściowe. Pracę sieci uznaje się za zakończoną w momencie, kiedy dwa kolejne wektory
wyjściowe są identyczne. Jeżeli sieć prawidłowo rozpoznała wektor wejściowy, to na wyjściu
powinien się pojawić ten wzorzec, który jest najbardziej do niego podobny.

Z funkcjonowania sieci o strukturze Hopfielda wynika, że służy ona do przekształcenia

obrazu wejściowego w inny obraz stanowiący jeden z wzorców.

UCZENIE

Uczenie sieci Hopfielda polega na jednorazowym ustaleniu wartości wag neuronów na

podstawie wzorców z ciągu uczącego. Ciąg uczący ma następującą postać:

U= (X

1

,X

2,

… , X

I,

… , X

I

)

Gdzie:
X

i

= (x

1

i

, x

2

i

, … , x

m

i

)

I

– Liczba wzorców

m

– liczba wejść/ wyjść sieci

Wartości wag

poszczególnych neuronów warstwy ustala się na podstawie zależności:

w

ik

=

Σ (x

i

m

* x

k

m

),

gdzie:
w

ik

– i-ta waga ki-tego neuronu

x

i

m

– i-ty element m-tego wzorca (dla i=1..n)

x

k

m

- k-ty element m-tego wzorca (dla k=1..n)

W jednej wadze zapisywane są informacje dotyczące kilku wzorców jednocześnie.

Powoduje to, iż przy choć najmniejszej próbie zmianie jednego wzorca należy proces uczenia
powtórzyć.



Sieć komórkowa – CNN (Cellural Neural Network)

BUDOWA.

Zawiera neurony usytuowane w przestrzennej siatce geometrycznej z wzajemnymi

powiązaniami. Specyficzne cechy sieci CNN znalazły zastosowanie w dziedzinie analizy
obrazów, w szczególności ze względu na możliwość równoległego i rozproszonego ich
przetwarzania. Odmienność sieci CNN od innych struktur polega także na tym, że do
żadnego z neuronów sieci nie jest wprowadzany cały wektor wejściowy opisujący
analizowany obiekt. W to miejsce definiuje się tak zwane sąsiedztwo, którego odmiany
wpływają na sposób działania sieci.

Sąsiedztwem

– jest zbiór wszystkich takich neuronów, które znajdują się nie dalej

niż o r wierszy w dół lub w górę, albo r kolumn w lewo lub w prawo od rozpatrywanego
neuronu.

Dla sieci CNN trudno jest, jak dla sieci wielowarstwowej czy posiadającej sprzężenie

zwrotne, wyróżnić poszczególne warstwy. W najprostszym przypadku neurony
umieszczane są w formie węzłów

siatki prostokątnej

o W wierszach i K kolumnach

(sieć komórkowa może mieć więcej wymiarów). W związku z tym, każdy z neuronów
można wyznaczyć jako

c

ij

, i=1..W,j=1..K.

Każdy z neuronów ma identyczną budowę oraz identyczną strukturę powiązań z

sąsiadującymi neuronami. W wypadku neuronów brzegowych występuje problem
zastąpienia brakujących sąsiadów w celu zachowania symetrii sieci. Jedną z możliwości
jest wprowadzenie stałych wartości brakujących sygnałów, jednak najczęściej stosuje się
metodę „zawijania”, wprowadzając jako sąsiadów neurony brzegowe z przeciwległego
brzegu struktury sieci.

Każdy z neuronów sieci przetwarza pojedynczy sygnał z analizowanego obrazu, co

oznacza, że jeżeli poddany analizie obraz składa się z W wierszy i K kolumn pikseli, to
sieć musi zawierać W*K neuronów umieszczonych w W wierszach i K kolumnach.

Wartości wag każdego z neuronów opisywane są przez macierz W

ij

postaci:

W

ij =

[W

ij

I,

W

ij

II,

W

ij

III

]

W

ij

I

– wagi należące do grupy sygnałów wejściowych (macierz ta nazywana jest

także macierzą sterowania),

W

ij

I

– wagi należące do grupy sygnałów zwrotnych (macierz ta nazywana jet także

macierzą sprzężenia zwrotnego),
W

ij

I –

współczynnik polaryzacji (wartość dodatnia oznacza pobudzenie sygnałów,

ujemna zaś ich hamowanie),

Funkcja aktywacji neuronów sieci CNN jest często przedziałowo-liniowa.

FUNKCJONOWANIE.

W sieci CNN, po wprowadzeniu na jej wejścia analizowanego obiektu zachodzą procesy

przejściowe, po których na jej wyjściach ustalają się wartości stanowiące odpowiedź sieci.
Równanie stanu neuronu

c

ij

można zapisać w postaci:

C de

ij

= - e

ij

/R + e

ij

I

+

e

ij

II

+

e

ij

III

,

Gdzie

e

ij

I

+

e

ij

II

+

e

ij

III

– sumaryczne pobudzenie neuronu.

C,R – stałe regulujące dynamikę procesów zachodzących w sieci.

Po wprowadzeniu sygnałów na wejścia sieci (liczba wejść powinna odpowiadać liczbie

elementów matrycy obrazu), na wyjściach pojawia się pierwszy stany przejściowy sieci. Do
obliczeń wykorzystywane są macierze W

I

oraz W

III

. Następnie obliczany jest kolejny stan,

jednak w tym przypadku włączona zostanie macierz W

II

– sumaryczne pobudzenie neuronu

zależy także od sygnałów pochodzących z wyjść sieci.

Duże znaczenie ze względów obliczeniowych oraz charakteru sieci CNN ma określenie

stopnia sąsiedztwa. Im wyższy stopień sąsiedztwa, tym struktura powiązań neuronów sieci
jest bardziej skomplikowana (trudniejsza do realizacji), a możliwości analizy obrazu większe.



Sieć Hamminga

BUDOWA.

Sieć Hamminga przeznaczona jest do rozpoznawania obiektów opisywanych pewnym

wektorem X=(x1,x2,..xm), GDZIE x

i

Є{

-1,1}, który jest podawany na wejście sieci. Wektor

uzyskiwany na wejściu sieci postać Y=(y1,y2, .. ym), gdzie y

i

Є

={R}. najczęściej wektor ten

określa numer klasy, do której został zaliczony badany obiekt X. Sieć ta stanowi złożenie
dwóch specyficznych warstw, dzięki czemu uzyskano narzędzie o ciekawych właściwościach.

Sieć składa się z dwóch warstw o jednakowej liczbie neuronów. Pierwsza warstwa

zawiera neurony o m wejściach (liczba elementów wektora wejściowego), druga zaś o n
wejściach (liczba neuronów w pierwszej warstwie). Neurony warstwy wejściowej połączone
są z neuronami warstwy wyjściowej na zasadzie „jeden do jednego” – pierwszy neuron
warstwy wejściowej przesyła sygnał do pierwszego neuronu warstwy wyjściowej. Warstwa
wyjściowa zawiera sprzężenie zwrotne do samej siebie (z pominięciem warstwy wejściowej).
Rozmiar wektora wejściowego X (liczba wejść sieci) jest zazwyczaj dużo większy od
rozmiaru wektora Y (liczba wyjść sieci).

FUNKCJONOWANIE.

Na wejścia neuronów warstwy wejściowej podawane są wektory X w celu ich

klasyfikacji. Na wyjściu sieci wynikowy wektor Y powinien zawierać na jednej z pozycji
wartość 1, a na pozostałych wartość 0. Indeks pozycji wektora Y, na której występuje wartość
1, jest numerem klasy rozpoznawanego obiektu. W wagach neuronów warstwy wejściowej
zapamiętywane są wzorce obiektów, co oznacza, że liczba rozpoznawanych klas jest zależna
od liczby neuronów. Po podaniu na wejściach wektora X, na wyjściu pierwszej warstwy sieci
otrzymujemy tak zwaną miarę Hamminga, która określa stopień podobieństwa wektora X do
zapamiętanych wzorców. Ponieważ w rozpatrywanym przypadku wagi mogą przyjmować
wartości ze zbioru {-1,1}, to miara Hamminga wyznacza liczbę pozycji, na których występuje
zgodność wartości.

Przykład:
Dla m=8 i X=(-1,1,1,1,-1,-1,-1,1}
Odległość od wektora W

1

=(1,1,1,1,-1,1,-1,-1} wynosi 5

a od wektora W

2

=(1,-1,1,1,1,1,1,-1}wynosi -2

Im większa wartość miary Hamminga, tym podobieństwo do zapamiętanego wzorca

klasy jest większe.

Wartości z wyjść pierwszej warstwy (miara Hamminga) przesyłane są na wyjście sieci

przez wagę równą 1 po przejściu sygnałów są one odłączone i nie uczestniczą w dalszym
procesie klasyfikacji. Wynika stąd, że w pierwszym kroku działania warstwy wyjściowej
dokonuje się bezpośredniego przeniesienia wyznaczonej miary Hamminga na wyjście sieci.
W tym pierwszym kroku rozpoczyna się iterację sygnałów, to znaczy wartości z tych wyjść
neuronów warstwy wyjściowej przekazywane są na wejścia tych neuronów. Sygnał z
pierwszego neuronu jest podawany na pierwsze wejście tego neuronu przez wagę o wartości
1, na drugie wejście drugiego neuronu przez wagę o wartości –ε , na trzecie wejście trzeciego
neuronu przez wagę o wartości –ε i tak dalej. Podobnie rzecz się ma z pozostałymi neuronami
warstwy wyjściowej. Sygnały z warstwy wejściowej nie brane są pod uwagę (warstwa ta po
podaniu pierwszych wartości zostaje odłączona).

Sieć Hamminga wykazuje duży procent poprawnych klasyfikacji obrazów, które są

uzyskiwane z wzorców poddanych zniekształceniom. Przy zakłóceniach losowych
pojedynczych elementów obrazu skuteczność ta znacznie spada. W związku z tym, liczba
wzorców zapamiętywanych przez sieć jest równa liczbie neuronów w jednej z warstw., to
pojemność sieci w stosunku do całkowitej liczby neuronów można określić jako:

P = N/2
GDZIE:
N - liczba neuronów w całej sieci

UCZENIE

Sieć Hamminga należy do typu sieci, które uczy się przez jednorazowe ustalenie

wartości wag zarówno w warstwie wejściowej (wyznaczającej odległość Hamminga), jak i w
warstwie wyjściowej (iterującej). W wagach neuronów zapamiętywane są wzorce z ciągu
uczącego, następującej postaci:

U = (X

1,

X

2

, … , X

i

, … , X

I

)

GDZIE:
X

i

= (x

1

i

, x

2

i

, … , x

m

i

)

I - liczba wzorców

Wartości wag w warstwie wejściowej ustalane są zgodnie z następującą
zależnością:
W

ij

= x

i

j

, i=1…m, j=1..n/2

Wagi neuronów w warstwie wyjściowej ustalane są zgodnie z zależnością:
W

ij

= { -

ε dla i rożnego od j, 1<=i<=n, 1<=j<=n

{1 dla i = j

Wartość –ε jest ustalana eksperymentalnie dl każdego indywidualnego przypadku z

założeniem, że jest ona mniejsza od 1.