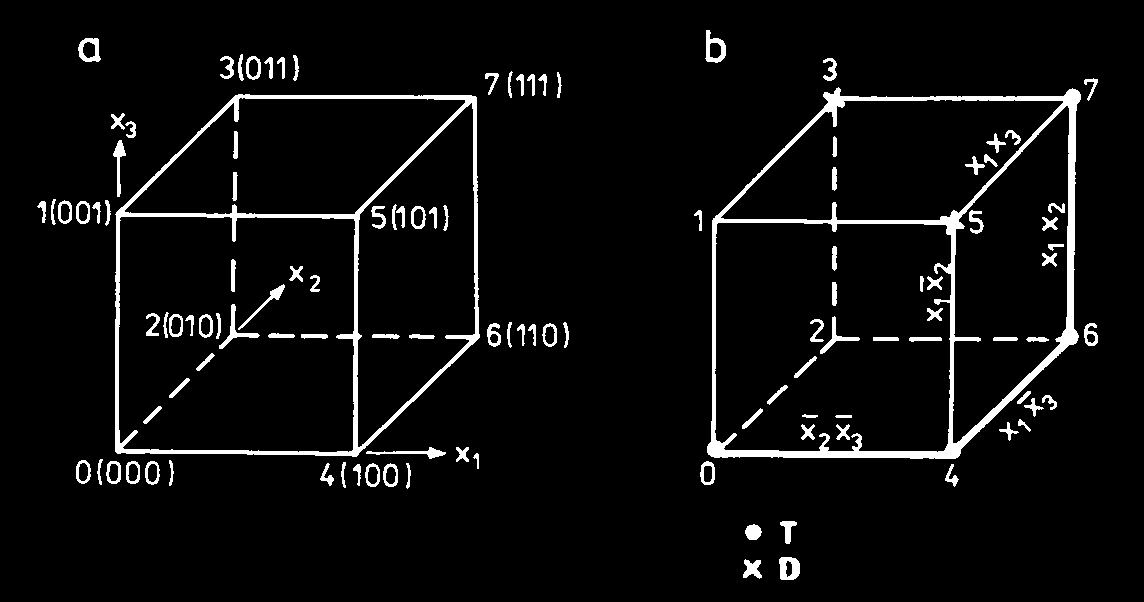F1-38

Minimalizacja „oparta na kostkach”

• Funkcję boolowską n zmiennych można przedstawić w postaci n-wymiarowej kostki ( n-kostki) – każdy wierzchołek

reprezentuje jeden z możliwych 2 n mintermów.

Wierzchołki oznacza się odpowiednimi liczbami dwójkowymi bk

lub równoważnikami dziesiętnymi k – zaznacza się wierzchołki, dla których k ∈ T lub k ∈ D.

• Zbiór 2 i wierzchołków n-kostki tworzy i-(sub)kostkę opisaną przez ( n – i) zmiennych.

• Wierzchołek n-kostki stanowi 0-kostkę opisaną n zmiennymi (odpowiada mintermowi).

• Krawędź łącząca dwa sąsiednie wierzchołki stanowi 1-kostkę

opisaną ( n – 1) zmiennymi.

Dwa wierzchołki są sąsiednimi, jeżeli opisujące je liczby

dwójkowe różnią się na jednej pozycji.

• 2-kostka jest kwadratem, a 3-kostka jest sześcianem.

• Geometryczna reprezentacja funkcji niezupełnej trzech

zmiennych:

T = {0, 4, 6, 7} i D = {3, 5}

© J. Kalisz, J. Pasierbiński, WAT, 2006