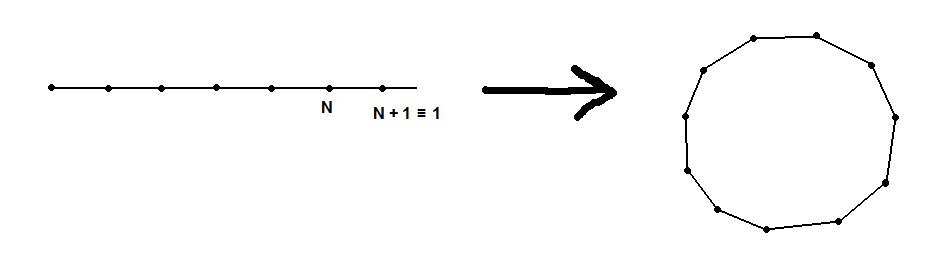Warunki periodyczności Borna-Karmana:
Aby opisać kryształ o skończonej liczbie N atomów, musimy atomowi o indeksie N + 1 przypisać numer 1.
Można sobie wyobrazić, że gdy mamy jednowymiarowy kryształ, zamykamy go w „kryształ cykliczny”: Z kolei kryształ 2-wymiarowy: w torus (nie sposób sobie wyobrazić analogicznej operacji na krysztale 3-wymiarowym, ale dokonujemy tego w rachunkach)
Funkcja Blocha musi zatem spełniać warunek: i k ( x+ N a ) x
1 1
e
u ( x + N a ) = eik x x u ( x)
k
1 1
k
, (gdy rozpatrujemy jeden kierunek, np. x ) i k N
x
1 1
a
e
= 1, gdy k N a = 2π n n = ,
1
,
2
,
3 ..., N
x
1 1
1 ,
1
1
Wynika stąd, że wektor falowy musi być równy: 2π n 1
k
=
n
x
a N
1
1
Analogicznie dla pozostałych kierunków: 2π n
2π n
2
k
=
3
k
=
n
n
y
a N
z
a N
2
2
3
3
Wszystkich atomów mamy N = N ⋅ N ⋅ N
1
2
3
3
2π
2π
2π
8π
Objętość komórki elementarnej: V =
⋅
⋅
= L ⋅ L ⋅ L =
, gdzie V - objętość kryształu k
a N
a N
a N
1
2
3
V
1
1
2
2
3
3
1
V
1
Gęstość stanów w przestrzeni kryształu: ρ( k) =
=
→
, jeśli przyjmiemy jednostkową objętość 3
3
V
8
k
π
8π
1
Gdy uwzględnimy spin, gęstość stanów wzrośnie dwukrotnie: ρ( ) = V
k
→
3
3
4π
4π