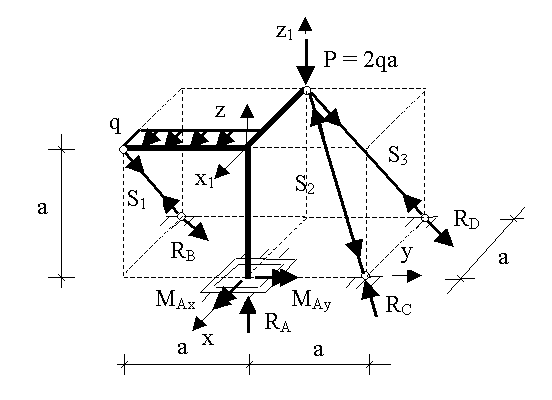
Przykład 5.7. Układ przestrzenny IV

Obliczyć reakcje i siły w prętach zakończonych obustronnie przegubami.

Przedstawiony element przestrzenny oparty jest za pośrednictwem teleskopu w punkcie A oraz na podporach przegubowych nieprzesuwnych w punktach B, C i D za pośrednictwem prętów dwuprzegubowych. W prętach (obustronnie zakończonych przegubami), które nie są obciążone w przęśle występują tylko siły osiowe. Z równowagi węzłów B, C i D wynika, że siły S1, S2 i S3 mają odpowiednio te same wartości i kierunki działania co reakcje RB, RC i RD.

Znamy więc kierunki nieznanych reakcji RB, RC i RD. Nie znamy ponadto trzech oddziaływań w podporze A: reakcji pionowej RA oraz momentów MAx i MAy. Dla przedstawionej na schemacie ramy można zapisać sześć warunków równowagi. Zatem układ jest statycznie wyznaczalny. Zapisując kolejne równania równowagi należy dążyć do tego, aby były to równania z jedną niewiadomą.

∑

a

1

2

M = 0 qa − R

a = 0 → R = qa

1

z

2

B

2

B

2

2

∑

1

qa

M = 0 M

+ R

a = 0 → M

= −

1

x

Ax

B

2

Ax

2

Znak minus oznacza, że zwrot wektora momentu MAx został założony przeciwnie do faktycznego.

∑

1

1

3

P = 0 − R

− R

+ qa = 0 → R = qa

ix

B

2

C

3

C

2

∑

1

1

2

P = 0 + R

− R

= 0 → R = qa

iy

D

2

C

3

D

2

∑

1

1

1

5

P = 0 R − R

+ R

− R

− 2 qa = 0 → R = qa

iz

A

B

2

C

3

D

2

A

2

∑

1

1

M = 0 M

+ qaa − R

a − 2 qaa − R

a = 0 →

2

M

= 2 qa

iy

Ay

B

2

D

2

Ay

2

W prętach zakończonych obustronnie przegubami występują siły: S = R = qa 1

B

2

3

2

(rozciągająca), S = R = qa

(ściskająca) i S = R = qa

(rozciągająca).

2

C

2

3

D

2

W celu sprawdzenia poprawności obliczeń korzystamy z warunku równowagi, z którego nie korzystaliśmy poprzednio

2

2

2

2

∑

a

1

1

1

qa

qa

qa

qa

M = 0 qa ⋅ − R

a − R

a + R

a = 0 →

−

+

−

= 0

iz

2

B

2

D

2

C

3

2

2

2

2

2