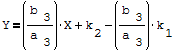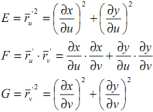Afiniczne odwzorowanie płaszczyzny na płaszczyznę Karol Bator
GGiIŚ, II rok, niestac.
grupa 1
DANE FORMALNO-PRAWNE:
1. Zleceniodawca: Akademia Górniczo-Hutnicza Wydział Geozdezji Górniczej i Inżynieri Środowiska 2. Wykonawca: Karol Bator
3. Czas wykonania: 15.05.2011
4. Rodzaj pracy: Afiniczne odwzorowanie płaszczyzny na płaszczyznę Dane dla N=104
Współrzędne na płaszczyźnie S1(xi,yi)
1 ( 2134.756,1354.809 ) [m]
2 ( 6119.535, 1703.432 ) [m]
3 ( 2695.117, 6422.938 ) [m]
Współrzędne na płaszczyźnie S2(Xi,Yi)
1 ( 3586.142, 4576.980 ) [m]
2 ( 7334.496, 5976.245 ) [m]
3 ( 2770.112, 9612.113 ) [m]
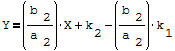
WYNIKI OBLICZEŃ:
1) Równania prostych parametrycznych dla u=const i v=const
–
dla u=const:
–
dla v=const:
Teoria: W odwzorowaniu afinicznym proste przechodzi w proste a linie parametryczne w linie parametryczne
2) Współczynniki Gaussa E, F, G
- dla powierzchni S1:
- dla powierzchni S2:
E1=1
E2=1,00064535
F1=0
F2=-0,000786336
G1=1
G2=1,000887919
Teoria: Na powierzchni oryginału linie parametryczne są do siebie prostopadłe (tworzą siatkę ortogonalną), natomiast na powierzchni obrazu linie parametryczne są do siebie prostopadłe.
3) Kąt miedzy liniami parametrycznymi
ΘS1= 90o00'00'
ΘS1= 90o02'42.07'
Teoria: Na powierzchni oryginału linie parametryczne są wzajemnie prostopadłe. Natomiast na powierzchni obrazu przecinają się pod kątem większym od 90°. Odwzorowanie nie jest więc wiernokątne, co pozwala obliczyć kierunki główne dla tego odwzorowania.
4) Skala odwzorowania
m1=1,00025529
m2=1,000775601
m3=1,000356541
Teoria: Elementarna skala zniekształceń to stosunek odpowiadających sobie elementarnych wielkości na powierzchni oryginału i na płaszczyźnie obrazu. Umożliwia obliczenie zniekształceń długości na podstawie skali długości.
5) Kierunki główne (I Tw. Tissota) k1=-1,16606511
k2=0,857585045
Teoria: W dowolnym regularnym odwzorowaniu, jeśli nie jest równokątne, istnieje jedna siatka ortogonalna na powierzchni oryginału, której obraz na drugiej powierzchni będzie również siatką ortogonalną – siatka krzywych głównych (I twierdzenie Tissota). Zgonie z punktem 3 rozpatrywane odwzorowanie nie jest równokątne, więc możliwe jest obliczenie kierunków głównych i wyznaczenie skal długości w kierunkach ekstremalnych, stanowiących parametry elipsy zniekształceń.
6) Skala w kierunkach głównych (I Tw. Tissota) a=1,00078083
b=0,9999855
Teoria: Obrazem elementarnych skal długości we wszystkich kierunkach wychodzących z danego punktu jest elipsa, której półosie są równe elementarnym skalom długości w kierunkach głównych. Umożliwia to określenie wartości zniekształceń, skal w kierunkach lini parametrycznych.
7) Skala w kierunkach lini parametrycznych (zależność między skalami)
- dla u=const:
- dla v=const
mu=1,000443861
mv=1,000322623
Teoria: Skale nie są sobie równe więc odwzorowanie nie jest równokątne (w odwzorowaniu występują zniekształcenia kątowe). Skale długości w kierunkach lini parametrycznych umozliwiają obliczenie skali pól.
8) Zniekształcenia kątów
β1=45o00'41.00'
β2=44o59'19.00'
9) Kąt o maksymalnym zniekształceniu
ωmax=0o02'43.98'
Teoria: Występujące w odwzorowaniu zniekształcenia kątowe określane są przez największą różnicę wartości bezwzględnej między kątem na powierzchni obrazu a odpowiadającym mu kątem na powierzchni oryginału.
f=1,00029681
zp=0,000766318
Teoria: Ze względu na to, iż f ≠ 1, odwzorowanie nie jest wiernopolowe.
Współrzędne na płaszczyźnie S1
Indywidualne zmienne modyfikujące
x
2134,765
y
1354,809
1
1
N
104
x
6119,535
y
1703,432
2
2
dY
N 0,005
dX
N 0,005
3
2
x
2695,117
y
6422,938
3
3
dY
N 0,005
dX
N 0,005
2
3
Współrzędne na płaszczyźnie S2
X
3586,142
Y
4576,980
1
1
X
7333,976 dX
Y
5976,765 dY
2
2
2
2
X
2770,632 dX
Y
9611,593 dY
3
3
3
3
Wzór odwzorowania punktów z płaszczyzny S1 na płaszczyznę S2
x
u
X
a
a
x
a
y
1
2
3
y
v
Y
b
b
x
b
y
1
2
3
OBLICZENIE WSPÓŁCZYNNIKÓW W ODWZOROWANIU AFINICZNYM
x
y
1
X
Y
1
1
1
1
x
y
A
1
X
Y
2
2
LA
2
LB
2
x
y
1
X
Y
3
3
3
3
1
1
a
A
LA
b
A
LB
1890,60570951
2701,371293423
a
0,96408254
b
0,266814927
0,267604787
0,963989417
Wyprowadzenie postaci linii parametrycznych prostych dla u=const oraz v=const X
a
a
u
a
v
X
a
a
u
a
v
1
2
3
1
2
3
S
S
2
Y
b
b
u
b
v
2
Y
b
b
u
b
v
1
2
3
1
2
3
u=const
v=const
k
a
a
u
1
1
2
k'
a
a
v
1
1
3
k
b
b
u
2
1
2
k'
b
b
v
2
1
3
X
k
a
v
1
3
X
k'
a
u
S
1
2
2
Y
k
b
v
S
2
3
2
Y
k'
b
u
2
2
X
k
X
k'
1
1
v
v
a
a
3
2
X
k 1
X
k'
Y
k
b
1
2
3
a
Y
k'
b
3
2
2
a 2
b
b
k
3
3
1
b
b
k'
Y
X
k
2
2
1
a
2
a
Y
X
k'
3
3
a
2
a
2
2
Postać parametryczna prostej dla u=const Postać parametryczna prostej dla v=const b
b
3
3
b
b
Y
X
k
k
2
2
a
2
a
1
Y
X
k
k
3
3
a
2
a
1
2
2
b 3
b
3,602287648
2
a
0,276755274
3
a 2
Równania linii stałych parametrów u i v na powierzchni S2
b
b
3
2
f1 x
x
f2 x
x
a
a
3
2
12
y
f2
8
f1
4
0
x
-4
-8
-8
0
8
-12
f1 x
f2 x
2. Wyznaczenie I formy kwadratowej oraz współczynników Gaussa 2
2
2
dS
E du
2 F du dv
G dv
Definicja funkcji parametrów u, v:
a
f u ; v
a
u
a
v
2
1
3
b
g u ; v
b
u
b
v
2
1
3
Powierzchnia S2
2
2
2
2
2
2
dS
E
du
2 F
du dv
G
dv
dS
E
du
2 F
du dv
G
dv
1
1
1
1
2
2
2
2
2
2
E
1
E
a
b
E
1,00064535
1
2
2
2
2
F
0
F
a
a
b
b
F
0,000786336
1
2
2
3
2
3
2
G
1
2
2
G
1,000887919
1
G
a
b
2
2
3
3
3. Obliczenie kąta pomiędzy liniami parametrycznymi.
F 1
180
Θ
arccos
Θ
1,570796327
rad
Θ
90 stopni
S1
E
G
S1
S1
π
1
1
F 2
Θ
arccos
Θ
1,571582061
rad
180
S2
E
G
S2
Θ
90,045019239 stopni
2
2
S2
π
SKALA ODWZOROWANIA
Współrzędne płaszczyzny S1 (xi,yi) i S2 (Xi, Yi) x
2134,765
y
1354,809
X
3586,142
Y
4576,98
1
1
1
1
x
6119,535
y
1703,432
X
7334,496
Y
5976,245
2
2
2
2
x
2695,117
y
6422,938
X
2770,112
Y
9612,113
3
3
3
3
Obliczenie długości na powierzchniach S1 i S2
2
2
2
2
d
x
x
y
y
d
X
X
Y
Y
112
2
1
2
1
212
2
1
2
1
2
2
2
2
d
x
x
y
y
d
X
X
Y
Y
123
3
2
3
2
223
3
2
3
2
2
2
2
2
d
x
x
y
y
d
X
X
Y
Y
131
1
3
1
3
231
1
3
1
3
Obliczenie kierunków dla boków trójkąta bok (i-i)
k
d1ii
d2ii
y
y
2
1
1-2
k
k
0,087488864
d
3999,991243619d
4001,012403073
12
x
x
12
112
212
2
1
y
y
2-3
3
2
k
k
1,378192148 d
5830,984095567d
5835,506611502
23
x
x
23
123
223
3
2
y
y
3-1
1
3
k
k
9,044545214
d
5099,012249892d
5100,83025483
13
x
x
13
131
231
1
3
na podstawie wzoru na skalę dla kierunków w trójkącie 2
E
2 F
k
G
k
2
2
12
2
12
m
m
1,00025529
1
2
1
1
k 12
2
E
2 F
k
G
k
2
2
23
2
23
m
m
1,000775601
2
2
2
1
k 23
2
E
2 F
k
G
k
2
2
13
2
13
m
m
1,000356541
3
2
3
1
k 13
kontrola
d 212
m'
m'
1,00025529
1
d
1
112
d 223
m'
m'
1,000775601
2
d
2
123
d 231
m'
m'
1,000356541
3
d
3
131
Kierunki główne odwzorowania:
2
2
G
E
G
E
4 F
2
2
2
2
2
k
k
1,16606511
1
2 F
1
2
2
2
G
E
G
E
4 F
2
2
2
2
2
k
k
0,857585045
2
2 F
2
2
kontrola
warunek poprawności: ki*kj=1
k
k
1
1
2
Skale w kierunkach linii parametrycznych: dla u=const (du=0)
G 2
m
m
1,000443861
u
G
u
1
wielkość zniekształcenia:
z
m
1
du
u
5
cm
z
0,000443861
z
10
44,386081395
du
du
km
E 2
m
m
1,000322623
v
E
v
1
wielkość zniekształcenia:
z
m
1
dv
v
5
cm
z
0,000322623
z
10
32,262275083
dv
dv
km
Skale i zniekształcenia długości w kierunkach głównych: 2
E
2 F
k
G
k
2
2
1
2
1
a
2
a
1,00078083
1
k 1
2
E
2 F
k
G
k
2
2
2
2
2
b
b
0,9999855
2
1
k 2
wielkość zniekształcenia:
z
a
1
z
0,00078083
da
da
z
b
1
z
0,0000145
db
db
Kąt o maksymalnym zniekształceniu:
a
b
180
ω
2 arcsin
ω
0,000795025 rad
ω
0,045551599 stopni
a
b
π
kontrola:
a
β
arctg
180
1
b
β
0,78559692 rad
β
45,0113879 stopni
1
1
π
b
180
β
arctg
β
0,785199407 rad
β
44,9886121 stopni
2
a
2
2
π
180
ω
2 β
β
ω
0,000795025 rad
ω
0,045551599 stopni
max
1
2
max
max
π
Skala i zniekształcenia pola:
skala
f
a b
f
1,000766318
zniekształcenie
z
f
1
z
0,000766318
p
p
kontrola
f'
a
b
a
b
f'
1,000766318
1
2
2
2