Ćwiczenie 21
„Wyznaczanie pracy wyjścia elektronów z metali metodą Richardsona.”
Wydział Mechatroniki
Alicja Zielińska; grupa 25; zespół 1
1. Wstęp.
Celem ćwiczenia jest zapoznanie się ze zjawiskiem termoemisji elektronów, wyznaczenie ich pracy wyjścia z metalu (katody lampy elektronowej) oraz pokazanie jak, metodą bezkontaktową, moŜna oszacować temperaturę gorącej powierzchni metalu. Termoemisją nazywamy zjawisko wychodzenia elektronów z rozgrzanej powierzchni danego ciała do otaczającej przestrzeni. Zjawisko to jest jednym z kilku zjawisk emisji elektronów pod wpływem dostarczonej energii.
Aby obliczyć pracę wyjścia musimy najpierw wyznaczyć temperaturę powierzchni emitującej, czyli katody. W tym celu do wzoru na gęstość prądu emisji Richarda –
Dushmana podstawiamy zaleŜność wysokości bariery potencjału od hamującej róŜnicy potencjałów:
2
Φ
e
eU
J
exp
exp
e = AT
−
⇒ Φ x = Φ + U ⇒ J
x
x = J
e
−
x
kT
kT
gdzie:
Je – gęstość prądu emisji,
A – stała Richardsona,
Φ - potencjał wyjścia,
Φx – wysokość bariery potencjału odległości x od katody, Ux – hamująca róŜnica potencjałów,
k – stała Boltzmana,
T – temperatura ciała,
Korzystając z otrzymanej zaleŜności moŜemy pośrednio wyznaczyć temperaturę powierzchni emitującej. W tym celu mierzymy zaleŜność prądu od hamującej róŜnicy potencjałów między katodą a anodą. Podstawiamy we wcześniejszym wzorze zamiast Jx wartość natęŜenia prądu anodowego Ia oraz Je = Ie, Ux = Ua. Logarytmujemy otrzymaną zaleŜność i dostajemy równanie prostej typu y = ax + b: eU
ln( I ) = ln( I
a
) −
a
e
kT
gdzie y = ln(Ia), x = Ua, b = ln(Ie) i z której nachylenia a=-e/kT moŜna wyznaczyć temperaturę katody:
e
T = − ka
Wyznaczając natęŜenie prądu termoemisji Ie z parametru b prostej dla róŜnych wartości temperatury T (róŜnych napiec Ŝarzenia) moŜna, korzystając ze wzoru na
I e =
W
2
AT exp
1
1
−
kT 1
I e =
W
2
AT exp
2
2
−
kT 2
gęstość prądu emisji, wyznaczyć pracę wyjścia: W=eΦ: Dzieląc stronami oba równania a potem logarytmując obie strony otrzymamy wyraŜenie na pracę wyjścia :
2
T T
I
T
W =
1 2
k
ln 1
e
2
T
T
I
T
1 −
2
e 2
1
gdzie Ie1, Ie2 – wartości prądu Ia dla Ua = 0, dla róŜnych napiec Ŝarzenia.
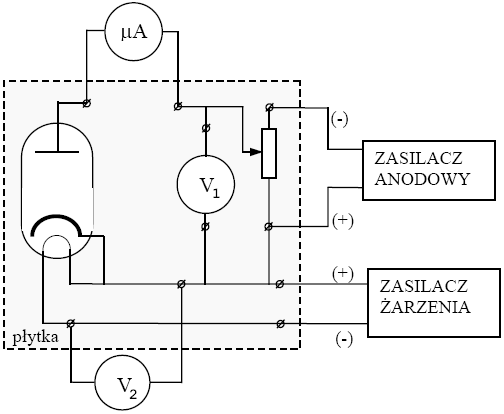
2. Układ pomiarowy.
Układ pomiarowy składa się z:
- zasilacza anodowego,
- zasilacza Ŝarzenia,
- katody próŜniowej lampy elektronowej (diody),
- woltomierza V1 typu V534 (zakres 10V, klasa: 0.3),
- woltomierza V2 typu LM1 (zakres 7.5V, klasa 0.5, liczba działek 75),
- mikroamperomierza µA (zakres 30µA, klasa 0.2, liczba działek 150), które połączone są tak, jak na schemacie:
1. Zestawiamy układ pomiarowy według schematu pamiętając, Ŝe dioda powinna być spolaryzowana w kierunku zaporowym;
2. Zasilamy obwód napięciem Ŝarzenia UŜ1 = 4.6V; 3. Mierzymy charakterystykę Ia = f(Ua) poczynając od Ia=0 aŜ do końca zakresu amperomierza;
4. Zmienić napięcie Ŝarzenia na UŜ2 = 5.8V i powtórzyć punkt 3; 4. Wyniki pomiarów i ich opracowanie.
Ia [A]
Ua1 [V]
Ua2 [V]
ln(Ia)
0
0,939
1,362
-
1,66667E-06
-
0,894
-13,3047
3,33333E-06
0,558
0,825
-12,6115
0,000005
-
0,784
-12,2061
6,66667E-06
0,496
0,757
-11,9184
8,33333E-06
-
0,735
-11,6952
0,00001
0,459
0,717
-11,5129
1,16667E-05
-
0,702
-11,3588
1,33333E-05
0,433
0,688
-11,2252
0,000015
-
0,677
-11,1075
1,66667E-05
0,413
0,666
-11,0021
1,83333E-05
-
0,657
-10,9068
0,00002
0,396
0,648
-10,8198
2,16667E-05
-
0,64
-10,7397
2,33333E-05
0,382
0,633
-10,6656
0,000025
-
0,626
-10,5966
2,66667E-05
0,37
0,619
-10,5321
2,83333E-05
-
0,613
-10,4715
0,00003
0,359
0,608
-10,4143
3,16667E-05
-
0,601
-10,3602
3,33333E-05
0,349
0,597
-10,309
3,66667E-05
0,34
0,587
-10,2136
0,00004
0,33
0,578
-10,1266
4,33333E-05
0,321
0,57
-10,0466
4,66667E-05
0,315
0,562
-9,97248
0,00005
0,312
0,555
-9,90349
Tabela 1. Wyniki pomiarów dla róŜnych napięć Ŝarzenia.
Otrzymane wartości natęŜenia logarytmujemy i dopiero wtedy uŜywamy do narysowania wykresu [ln(Ia)=f(Ua)].
Dokonując przybliŜenia liniowego na wykresach zaleŜności logarytmu naturalnego z Ia od Ua otrzymujemy wskaźnik przybliŜenia bardzo bliski jedynki (0,9998
dla UŜ1 oraz 0,99996 dla UŜ2) co oznacza, Ŝe wyniki naszych pomiarów przebiegały liniowo i nie ma potrzeby pomijania odstających punktów pomiarowych (poniewaŜ
właściwie takie nie istnieją).

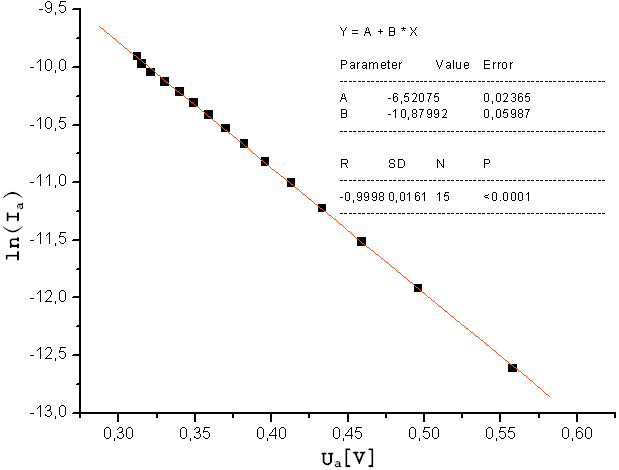
1. Wykres zaleŜności logarytmu naturalnego z natęŜenia od napięcia dla UŜ1.
Współczynniki odczytane za pomocą linearyzacji programu Origin: a1 = -10,87992 ± 0,05987
b1 = -6,52075 ± 0,02365
2. Wykres zaleŜności logarytmu naturalnego z natęŜenia od napięcia dla UŜ2.
b2 = -4,30906 ± 0,01202
PoniewaŜ program Origin zapisuje prostą równaniem y = a + bx zamieniamy oznaczenia współczynników, aby otrzymać interesujące nas równanie y = ax + b.
Wyliczamy wartości prądów Ie ze wzoru:
I = exp( b)
e
czyli:
I
= exp -
( 10,8799 )
= 0,001472564 A ≈ ,
1 47 mA
e 1
I
= exp -
( 10,0546
8 )
= 0,0134461 3
8 A ≈ 1 ,
3 45 mA
e 2
Obliczamy temperatury katody ze wzoru:
e
T = −
czyli:
ka
e
1,6 *10-19
T = −
= −
= 1066,593092K ≈ 1066,6 K
1
ka
1.38 *10-23 * (-10,87992 )
1
e
1,6 *10-19
T = −
= −
= 1154,133947K ≈ 1154,13K
2
ka
1.38 *10-23 * (-10,87992 )
2
Wartość pracy wyjścia wyliczamy ze wzoru podanego we wstępie: 2
2
T T
I
T
1
2
1
2
-23
1066,6 *1154,13
,
0 001472564 1154,13
W = k
e
ln
= 1.38*10 *
* ln
=
T − T
I
T
1066,6 -1154,13
,
0 013446183 1066,6
1
2
e 2
1
3,98764 *10 1-9 J ≈
e
5
,
2
V
5. Rachunek błędów.
1. Błędy systematyczne przyrządów:
a) Woltomierz cyfrowy – tylko błąd dyskretyzacji: δ=0,001V
b) Woltomierz analogowy:
klasa * zakres
zakres
%
5
,
0
* 5
,
7
5
,
7
δ =
+
=
+
= 0
,
0 87 V
5
10 %
0
2 * liczbadzi l
a ek
10 %
0
2 * 75
c) Mikroamperomierz:
zakres
δ
,
0 2% * 30
30
=
+
=
+
= 1
,
0 6 A
µ
100%
2 * liczbadzialek
100%
2 *150
2. Wyznaczanie błędu całkowitego wyznaczenia temperatury (metoda róŜniczki zupełnej):
e
,
1 6 *10−19
∆ T =
* ∆ a =
* ,
0 06 ≈ 8
,
5 7 K
1
2
1
ka
3
,
1 8 *10−23 * (−10 8
,
)
8 2
1
e
,
1 6 *10−19
∆ T =
* ∆ a =
* ,
0 02 ≈ ,
2 07 K
2
2
2
ka
3
,
1 8 *10−23 * (−1 ,
0 0 )
5 2
Ostatecznie:
T1 = 1067 ± 6 K
T2 = 1154,13 ± 2,07 K
3. Błąd systematyczny natęŜenia (metoda róŜniczki zupełnej): I
∂ e
a
= e
a
∂
I
∂
I
e 1
∆
=
= ea 1 * a
∆ = e(-10,88)
-06
* 0,06 ≈ 1,13 *10
A
e 1
1
∂ a 1
I
∂ e 2
a 21
( 1-0,055)
I
∆
=
= e * a
∆ = e
-07
* 0,018 ≈ 7,75 *10
A
e 2
2
∂ a 2
Ostatecznie:
Ie1 = 1470 ± 1,13 µA
Ie2 = 13450 ± 0,775 µA
4. Całkowity błąd pracy wyjścia obliczony metodą róŜniczki zupełnej:
2
2
∂ W
kT
I
T
kT
2
1
e
2
2
= −
ln
W
∂
kT T
∂
1 2
T
T
T
I
T
T
T
=
1
( 1 − 2 )2
+
e 2 1
1 −
2
I
∂
( T − T ) I
1
e
1
2
1
e
2
2
∂
∂
−
W
kT
I
T
kT
W
kT T
1 2
1
1
e
2
1
= −
=
ln
∂
∂
−
T
I
( T
T ) I
T
T
I
T
T
T
e 2
1
2
e 2
2
( 1 − 2 )2
+
e 2 1
1 −
2
∂
W
∂
W
∂
W
∂
W
∆ =
* T
∆ +
* T
∆ +
* I
∆ +
* I
∆
=
T
1
∂
T
2
∂
I
e 1
∂
I
e 2
∂
1
2
e 1
e 2
= 5,111*10-21 * 8
,
5 7 + 4,378 *10-21 * ,
2 07 -1,32 *10 1
- 6 * 1
,
1 3 *10−6 + 1,444 *10 1-7 * 7,75 *10−7 =
= 3,89 *10-20 J ≈ ,
0 24 e
3 V
Ostatecznie:
W = (4 ± 0,4 ) * 10-19 J = 2,5 ± 0,25 eV
6. Wnioski.
Wykonanie ćwiczenia pozwoliło nam wyznaczyć liniową zaleŜność logarytmu naturalnego prądu od róŜnicy potencjałów między katodą i anodą. ZaleŜność ta pozwoliła nam na wyznaczenie temperatury katody dla dwóch róŜnych napięć Ŝarzenia a następnie przybliŜoną pracę wyjścia elektronów z katody. MoŜemy zauwaŜyć, Ŝe niepewność wyznaczenia wartości pracy wyjścia jest mała chociaŜby ze względu na to, Ŝe zakładamy iŜ stała Richardsona została podana bezbłędnie i jest stała (kiedy w rzeczywistości zaleŜy od temperatury). MoŜna powiedzieć, Ŝe ćwiczenie ma charakter poglądowy. Głównym jego celem jest zapoznanie studentów ze zjawiskiem termoemisji oraz pokazanie jak pośrednio moŜna wyznaczyć temperaturę katody i pracę wyjścia.
Nie jesteśmy w stanie jednoznacznie określić na podstawie samej pracy wyjścia z jakiego materiału zrobiona jest katoda. Mógłby to przykładowo być rubid (2,16 eV), poniewaŜ jego praca wyjścia zbliŜona jest do tej wyznaczonej doświadczalnie, ale jego temperatura topnienia jest duŜo niŜsza od tej wyznaczonej doświadczalnie i katoda z niego wykonana stopiłaby się (co nie nastąpiło). Jednoznacznie określić materiał
pozwoliłoby porównanie charakterystyk temperatury od napięcia Ŝarzenia dla katod z róŜnych substancji.