Probabilistyka i statystyka – ćwiczenia (14.10.2010) Zmienna losowa dyskretna (skokowa)
= ,,… ,
: Ω →
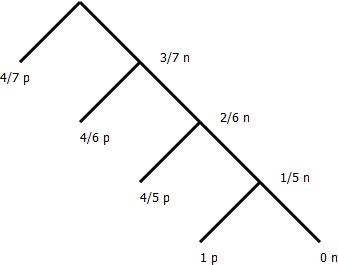
Rzucamy kostką. Zmienna losowa przyjmuje wartość liczby oczek. Znajdź
1) Rozkład zmiennej losowej 2) Wartość oczekiwaną () 3) Wariancje i odchylenie standardowe (), = () 4) Dystrybuantę
Ad. 1
1
2
3
4
5
6
1
1
1
1
1
1
6
6
6
6
6
6
Ad. 2
1
1
1
1
1
1
() = Σ ! ∗ = 1 ∗ 6 + 2 ∗ 6 + 3 ∗ 6 + 4 ∗ 6 +5 ∗ 6 + 6 ∗ 6 = 3,5
Ad. 3
() =$%& [( − ())
() = () − ()
35
() =$%& (1 − 3,5) + (2 − 3,5) + (3 − 3,5) + (4 − 3,5) + (5 − 3,5) + (6 − 3,5) = 12
1 4 9 16 25 36 91
() = 6 + 6 + 6 + 6 + 6 + 6 = 6
91 49 182 − 147 35
() = () − () = 6 − 4 = 12 = 12
= -35
12
1
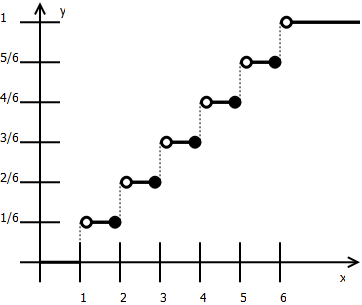
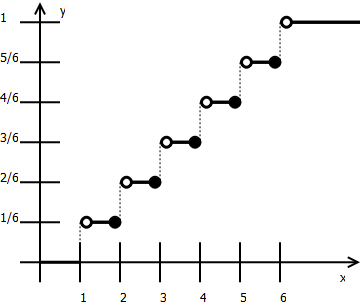
Ad. 4
0, / ∈6 1
31
116,1 7 / 6 2
12
116,2 7 / 6 3
.(/) = 3
9
26 , 3 7 / 6 4
14
116,4 7 / 6 5
15
16,5 7 / 6 6
0 1, / 8 6
Cechy dystrybuanty
1) niemalejąca
2) lewostronnie ciągła 3) lim=→>? .(/) = 0, lim=→? .(/) = 1
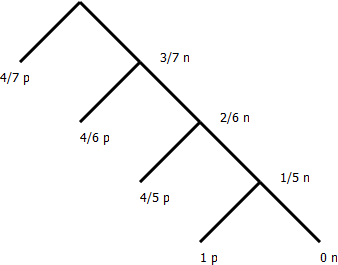
2. Ze zbioru liczb 2,3,4,5,6,7,8
lo
l suj
u e
j m
e y
y b
e
b z
z zw
z ra
r c
a an
a i
n a
i
a po
p je
j dn
d e
n j
j li
l c
i z
c b
z i
b e
i i
i końc
ń zy
z m
y y gr
g ę
r gd
g y
d
wylosujemy liczbę parzystą.
a)
a pa
p r
a z
r y
z sta
a wy
w lo
l so
s wa
w n
a a
n
a za
z
a 1
ra
r z
a e
z m
e – wygrywamy samochód za 5 zł
b) nieparzysta za 1,
, pa
p r
a z
r y
z sta
t
a za
z
a 2 – wy
w gr
g y
r w
y am
a y pr
p a
r l
a k
l ę w
ko
k lo
l ro
r w
o ej
j ga
g z
a e
z c
e ie
i za
z
a 2
zł
z
c) ni
n e
i pa
p r
a z
r y
z st
s a
a za
z
a 1
,2,
, pa
p r
a z
r y
z s
y ta
a za
z
a 3
3 – 1 zł
d)
d ni
n e
i pa
p r
a z
r y
z sta
a za
z
a 1,2
, ,3
, , pa
p r
a z
r y
z sta
a za
z
a 4
– przegrywamy 30 zł
Obl
b i
l c
i z
z pr
p z
r e
z cię
i tną
n
ą k
wo
w tę
t wy
w g
y r
g a
r n
a ą
n
ą lu
l b
u
b pr
p z
r e
z gr
g a
r n
a ą
n
ą w po
p jed
e y
d ńc
ń ze
z j
j gr
g z
r e
z
−30
1
2
5
2
8
2
4
70
70
7
7
4
@(A) = 7
3 4 2
@(A) = 7 ∗ 6 = 7
2
3 2 4
8
@(AB) = 7 ∗ 6 ∗ 5 = 70
3 2 1
2
@(AC) = 7 ∗ 6 ∗ 5 ∗ 1 = 70
2
8
2
4
60
8
40 200 188 84
= ΣC! = −30 ∗ 70 + 1 ∗ 70 +2 ∗ 7 + 5 ∗ 7 = −70 + 70+ 70 + 70 =
70
35
Autor: she
h n
e l
n on
o
n (http://shenlon.eu)
3