Rozkład t Studenta Michał Urban Wrocław 2006
Rozkład t Studenta
Rozkład Studenta zwany rozkładem t lub rozkładem t-Studenta (zwany dalej rozkładem) to ciągły rozkład prawdopodobieństwa często stosowany w statystyce podczas testowania hipotez i przy ocenie błędów pomiaru. Rozkład t jest symetryczny względem prostej x=0 oraz bardzo zbliŜony kształtem do rozkładu normalnego standaryzowanego.
Przez długi czas pojawiały się problemy przy szacowaniu parametrów i weryfikacji parametrów w przypadku małych prób (n < 30), a jedyną zalecaną metoda było zwiększenie liczebności próby. Propozycje rozwiązania tego problemu przedstawił W. Gosett w 1908 roku
, pisząc pod pseudonimem Student. Chciał on przewidzieć liczbę beczek do wymiany w ciągu najbliŜszego roku. Podał on funkcję zaleŜną od wyników pomiarów Xi i niezaleŜ na od σ 2
( odchylenie standardowe z populacji).W 1916 r. R.A.Fisher znalazł funkcję gę stoś ci oraz dystrybuantę dla omawianego rozkładu i nazwał go rozkładem Studenta.
Gdy niezaleŜne zmienne losowe X1, X2, X3,..., Xn mają jednakowy rozkład normalny
N(µ , σ ), to ich średnia arytmetyczna X ma takŜe rozkład normalny.
Rozkład Studenta jest rozkładem zmiennej losowej : X − µ
t =
v
s
gdzie : S to odchylenie standardowe z próby
n
1
S =
∑( Xi − X 2) ;
n −1 i=1
v = n-1 - liczba stopni swobody (Liczba stopni swobody to liczba niezaleŜ nych obserwacji okreś lają ca statystykę )
Funkcją gęstości rozkładu t Studenta nazywamy wyraŜenie :
n
n
Γ
−
2
2
2
t
f ( t) =
1
+
v
v
Γ vπ
2
Dystrybuantę rozkładu Studenta moŜna zapisać w postaci: α
t
F t
( ) = P( t < tα ) = 2∫ f t ( ) dt
0
gdzie α jest poziomem istotności
Podstawowe własności rozkładu :
• E(t) = 0 wartość oczekiwana
•
n −1
D( t) =
wariancja dla n>3
n − 3
1
Rozkład t Studenta Michał Urban Wrocław 2006
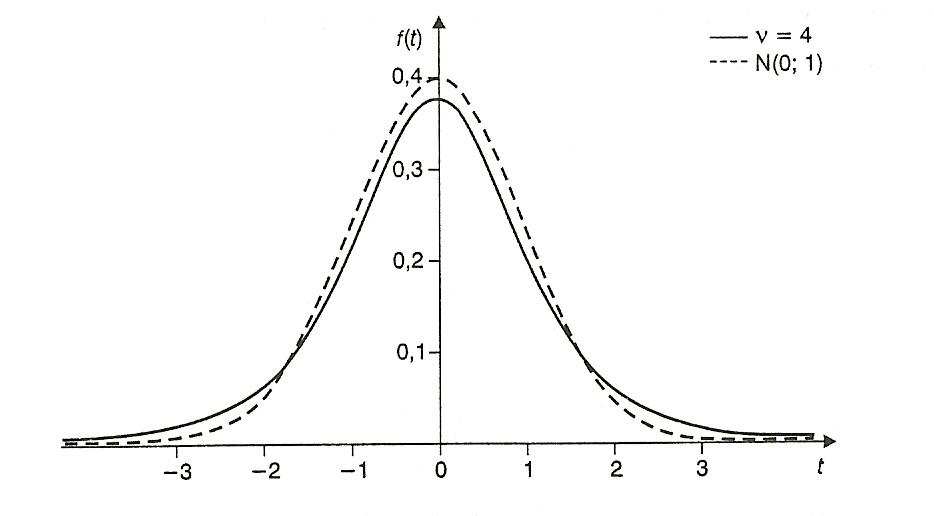
Wartość wariancji D(t) jest jak widać ze wzoru liczba zawsze większą od 1. DąŜy ona do 1 gdy liczba stopni swobody dąŜy do nieskończoności. Oznacz to Ŝe rozkład t Studenta zmierza do standardowego rozkładu normalnego gdy liczba próby rośnie do nieskończoności. Jest to widoczne na rysunku poniŜej.
Rysunek1. Wykres funkcji gę stoś ci rozkładu t Studenta z 4 stopniami swobody i rozkładu normalnego N(0;1)
Podobnie jak w rozkładzie standardowym w rozkładzie t Studenta moŜna wyznaczyć wartość tα,v dla których spełniona będzie relacja : P(− α
t
t
t
, v <
< α )
, v
= 1−α
Istnieją Tablice rozkładu t Studenta Dla róŜnych α (0 < α < 1) oraz róŜnych v (1< v < ∞) . Tablice takie moŜna tworzyć dowolnie w arkuszu kalkulacyjnym.
Zastosowania
Rozkład t Studenta stosowany jest w estymacji przedziałowej, w testach parametrów w szczególności dla średnich, wariancji oraz w testach istotności parametrów statystycznych
– gdy mamy do czynienia z małymi próbami (najczęściej przyjmuje się Ŝe próba jest mała gdy jej liczebność n < 30). Ponadto rozkład Studenta znajduje zastosowanie przy weryfikacji niektórych hipotez dotyczących średniej, gdy dysponuje się mała próbą, czli wtedy gdy nie moŜna wykorzystać rozkładu normalnego, oraz przy sprawdzaniu wątpliwych wyników obserwacji.
2
Rozkład t Studenta Michał Urban Wrocław 2006
Tablice wartoś ci tα ,v rozkładu t Studenta 0,2
0,1
0,05
0,02
0,01
0,002
0,001
4
1,53321 2,13185 2,77645 3,74694 4,60408 7,17293 8,61008
5
1,47588 2,01505 2,57058 3,36493 4,03212 5,89353 6,86850
6
1,43976 1,94318 2,44691 3,14267 3,70743 5,20755 5,95872
7
1,41492 1,89458 2,36462 2,99795 3,49948 4,78525 5,40807
8
1,39682 1,85955 2,30601 2,89647 3,35538 4,50076 5,04137
9
1,38303 1,83311 2,26216 2,82143 3,24984 4,29689 4,78089
10
1,37218 1,81246 2,22814 2,76377 3,16926 4,14366 4,58676
11
1,36343 1,79588 2,20099 2,71808 3,10582 4,02477 4,43688
12
1,35622 1,78229 2,17881 2,68099 3,05454 3,92960 4,31784
13
1,35017 1,77093 2,16037 2,65030 3,01228 3,85204 4,22093
14
1,34503 1,76131 2,14479 2,62449 2,97685 3,78743 4,14031
15
1,34061 1,75305 2,13145 2,60248 2,94673 3,73286 4,07279
16
1,33676 1,74588 2,11990 2,58349 2,92079 3,68615 4,01487
17
1,33338 1,73961 2,10982 2,56694 2,89823 3,64576 3,96511
18
1,33039 1,73406 2,10092 2,55238 2,87844 3,61048 3,92174
19
1,32773 1,72913 2,09302 2,53948 2,86094 3,57933 3,88332
20
1,32534 1,72472 2,08596 2,52798 2,84534 3,55183 3,84956
21
1,32319 1,72074 2,07961 2,51765 2,83137 3,52709 3,81930
22
1,32124 1,71714 2,07388 2,50832 2,81876 3,50497 3,79223
23
1,31946 1,71387 2,06865 2,49987 2,80734 3,48497 3,76764
24
1,31784 1,71088 2,06390 2,49216 2,79695 3,46678 3,74537
25
1,31635 1,70814 2,05954 2,48510 2,78744 3,45019 3,72514
26
1,31497 1,70562 2,05553 2,47863 2,77872 3,43498 3,70666
27
1,31370 1,70329 2,05183 2,47266 2,77068 3,42101 3,68949
28
1,31253 1,70113 2,04841 2,46714 2,76326 3,40820 3,67392
29
1,31143 1,69913 2,04523 2,46202 2,75639 3,39627 3,65952
30
1,31042 1,69726 2,04227 2,45726 2,74998 3,38521 3,64598
Literatura:
• „Statystyka dla inŜynierów” Witold Klonecki Wydawnictwo Naukowe PWN Warszawa 1999
• „Statystyka dla studiów licencjackich” Radosław Podgórski Polskie Wydawnictwo Ekonomiczne Warszawa 2005
• http://pl.wikipedia.org/wiki/Rozk%C5%82ad_t-Studenta - www.wikipedia.org 3