Równanie ruchu obrotowego zadania
1. Obliczyć przyspieszenie mas m1 i m2 zawieszonych na nieważkiej, nierozerwalnej nici przerzuconej przez blok obracający się bez tarcia. Blok ma moment bezwładności I i promień R. Nić nie ślizga się po bloku. Obliczyć naciąg T1 i T2 nici.
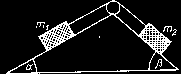
2. Na podwójnej równi pochyłej o kątach nachylenia
α = 30o, β = 45o umieszczone są dwa ciała o masach
m1 = 500 g i m2 = 100 g (rys.), połączone nitką prze-
rzuconą przez bloczek o masie m3 = 200g i promieniu
R = 10 cm. Współczynnik tarcia obu ciał o równię
wynosi µ = 0,25. Oblicz wartość przyspieszenia,
z jakim poruszają się oba ciała.
3. Na szczycie równi umocowany jest blok o masie m
i promieniu R, przez który przerzucono nić. Do końców nici
przymocowane są obciążniki o masach m1 i m2 (rys.). Oblicz
przyspieszenie obciążników i siłę napinającą nić zakładając,
że opory ruchu są do zaniedbania. Kąt nachylenia równi do
poziomu wynosi α. Przyjmij, że obciążnik m2 opada w dół.
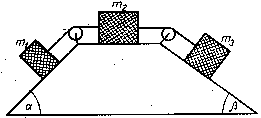
4. Wprowadź wzór na przyspieszenie ciał i napięcia nici
w układzie pokazanym na rysunku. Masa obydwu
bloków wynosi m4 zaś ich promień R. Opory ruchu są do
pominięcia.
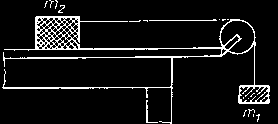
5. Oblicz przyspieszenie liniowe obciążników
przedstawionych na rysunku obok, których masy
wynoszą m1 = 50 g i m2 = 150 g. Współczynnik
tarcia obciążnika m2 o stół wynosi f = 0,1, natomiast
moment bezwładności bloczka wynosi I = 0,003 kg ⋅
m2, a jego promień R = 10 cm.