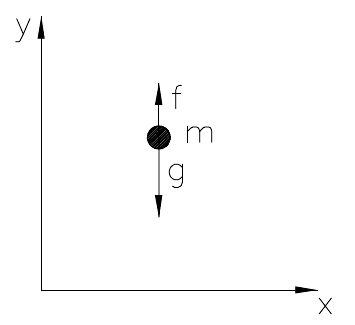
Rozważmy ciało w kształcie małej kulki o masie m, które potraktujemy jako punkt materialny poruszający się w kierunku osi y w polu ciężkości pod wpływem sił f i siły ciężkości mg, jak pokazano na rysunku.
Rys. Masa punktowa w ruchu w polu ciężkości z siłą oporu f.
Mamy tu:
y
m
f mg
(1)
Zauważmy, że lewą stronę równania można zapisać: d
1
2
y
m
y
m
d
d
K
y
m
(2)
dt
dt y 2
dt
y
1
gdzie
2
K
y
m jest energią kinetyczną.
2
Natomiast siłę grawitacji możemy wyrazić w funkcji energii potencjalnej P , jako:
mg
P
mgy
(3)
y
y
P mgy - jest energią potencjalną grawitacji.
Zdefiniujmy teraz funkcję będącą różnicą energii kinetycznej i potencjalnej: 1
L K P
y
m 2
mgy
(4)
2
L
K
L
P
i zauważmy, że:
i
y
y
y
y
wobec tego (1) możemy zapisać w postaci:
d
L
L
f
(5)
dt y
y
Funkcję L będziemy nazywali lagrangianem (lagranżjanem) układu a równanie (5) równaniem Lagrange’a.
Rozważmy teraz k punktów w przestrzeni 3D, których położenie jest określone wektorami położenia r ,.... r
. . Jeśli punkty te mogą poruszać się bez ograniczeń, to sformułowanie ich równań ruchu można 1
k
wykonać korzystając z równań zmiany pędów pod wpływem sił zewnętrznych. Założymy jednak, że na punkty te nałożono więzy, które stanowią ograniczenia ich ruchu względnego, co wymaga uwzględnienia w równaniach sił reakcji tych więzów.
Przykładem więzów może być połączenie dwóch wybranych punktów rozpatrywanego zbioru sztywnym i nieważkim prętem, wtedy musi być spełniona zależność: T
r r
l ,
r r
r r
,
1
2 1
2
2
l
1
2
W tym wypadku oprócz sił zewnętrznych na każdy z punktów z dodatkowymi więzami działa siła tych więzów. Dla celów analizy dynamicznej układu możliwe są dwa różne podejścia; w metodzie pierwszej trzeba wyznaczyć siły więzów i uwzględnić je w analizie wraz z siłami zewnętrznymi, korzystniejsza jest jednak taka metoda analizy układu w której nie będzie potrzebna znajomość wartości sił więzów.
Więzy nałożone na współrzędne r ,.... r
. mogą spełniać dodatkowe zależności, np. postaci: 1
k
g r
r
dla i= 1,..., l
i
,.....,
1
k 0,
i wtedy nazywamy je holonomicznymi (całkowalnymi), natomiast w innym wypadku będą nosić nazwę nieholonomicznych.
Typowym przykładem więzów nieholonomicznych są więzy jednostronne określone dla punktu materialnego w postaci: r , gdzie jest stałym promieniem powierzchni kulistej o środku w początku układu. Działanie więzów istnieje zawsze wtedy, gdy punkt znajduje się wewnątrz sfery kulistej lub na jej powierzchni, natomiast siły oddziaływania więzów pojawią się tylko wtedy, gdy punkt jest w kontakcie ze ścianką sfery.
Jeżeli na układ nałożymy l więzów holonomicznych, to ograniczymy jego liczbę stopni swobody o l.
Wobec tego współrzędne k -punktów można wyrazić przez n współrzędnych uogólnionych q ,....., q 1
n
r r q ,....., q
,
i ,
1 .. k
.
i
i 1
n
gdzie współrzędne q ,....., q są niezależne 1
n
Rozważmy teraz zbiór nieskończenie małych przesunięć zgodnych z więzami r ,....., r
, które
1
k
nazwiemy przesunięciami przygotowanymi albo wirtualnymi. Działając tymi przesunięciami na bieżące wartości więzów np. r r
, r r
układ nadal spełnia równania więzów, co zapiszemy 1
1
2
2
r r
r r
r r r r
1
1
T
l
2
2 1
1
2
2
2
Wykonując działania i odrzucając człony kwadratowe z r , r
dostaniemy
1
2
T
r r
r r
1
2
1
0
2
Ogólnie układ przesunięć przygotowanych można wyrazić wzorem n
r
r
i
q
,
i ,
1 .. k
.
i
j
q
1
j
j
W równowadze dynamicznej przaca wykonana przez układ przesunięć przygotowanych jest równa zeru, czyli
n
T
F
r
0
i
i
j 1
a
gdzie F jest siłą całkowitą działającą na punkt i-ty tj. sumą siły zewnętrznej f i siły więzów f
.
i
i
i
Załóżmy, że praca całkowita sił więzów odpowiadająca dowolnemu układowi przesunięć przygotowanych jest równa zeru, tzn.
k
a T
f
r
i
0
i
i 1
Z ostatnich dwóch wzorów otrzymamy:
f T r
0
i
i
i 1
co wyraża zasadę prac przygotowanych
Należy tu zaznaczyć, że siły f indywidualnie nie są równe zeru.
i
Rozważmy teraz układ w stanie ruchu, w którym na każdy i-ty punkt materialny działa siła d’Alemberta p
i
zapewniając w ten sposób równowagę. Wtedy zastępując siłę F siłą F p
otrzymamy równanie:
i
i
i
k
k
T
f
r
T
p
r
0
,
i
i
i i
i 1
i 1
gdzie dowolny r nie zawsze jest równy zeru.
i
Wobec tego praca przygotowana sił f określona jest zależnością: i
k
k
n
n
r
T
f r
f
i
i
T i q
q
i
j
1
1
1
q
i
i
j
j
j
j
j 1
k
r
gdzie
T
i
f
0 - jest siłą uogólnioną, która nie musi mieć wymiaru siły jak i q nie musi być j
i q
i
i
1
j
długością, jednak
q
musi mieć wymiar pracy.
j
j
Ponieważ p
m r , więc
i
i i
k
k
k
n
r
T
T
T
i
p r
m r
r
m r
q
i
i
i i i i i
j
1
1
1
1
q
i
i
i
j
j
Różniczkując dostaniemy
k
r
r
r
T
k
d
d
d
i
T
i
T
m r
m r
m
i
r
i i
i i
i i
1
q
1
dt
q
dt
q
i
j
i
j
j
n
r
v
r
ale v
r
i q ,
czyli
i
i
i
i
j
q
q
1
q
j
j
j
j
Wobec tego
n
d
r
2r
v
i
i
q
i
l
dt
q
1 q
q
q
j
l
j
l
j
i dalej
k
k
r
d
v
d
dv
i
T
i
T
m rT
m v
m v
i i
i i
i i
i
1
q
1
dt
q
dt
q
i
j
i
j
j
Z definicji energia kinetyczna
k
1
K m vTv
i
i
i
2
i 1
Stąd
k
d
K
K
T
i
m
r
r
i i
1
q
dt q
q
i
j
j
j
oraz
k
n d K
K
T
p r
q
i
i
j
1
1
dt
q
q
i
j
j
j
w końcu
K
q
j
0
j
dt q
q
j
1
j
j
Wobec tego pamiętając, że przesunięcia przygotowane są niezależne, więc wszystkie współczynniki w ostatnim równaniu muszą być równe zeru a więc: d
K
K
,
j ,
1 .. n
.
j
dt q
q
j
j
Ponadto, jeśli siła uogólniona jest sumą zewnętrznej siły uogólnionej i siły w polu potencjalnym to j
zakładając, że istnieją i V q spełniające zależność j
V
j
j
q
j
Otrzymamy
d
L
L
j
dt q
q
j
j
gdzie V jest energią potencjalną pola a L K V jest lagrangianem.