Dark

Energy

and

struture

formation

Lua

Amendola,

INAF/O

AR

amendolamp

orzio.astro.it.

7th

Otob

er

2005

0-0

•

Gra

vit

y

,

expansion

and

aeleration

•

Cosmologial

observ

ations

•

Dark

energy:

linear

and

non-linear

prop

erties

0-1

Historial

p

ersp

etiv

e,

ira

350

b..e.

•

Gra

vit

y

is

alw

a

ys

attrativ

e.

•

Aristotle

's

problem:

ho

w

to

a

v

oid

that

the

sky

falls

on

our

head?

0-2

Historial

p

ersp

etiv

e,

ira

1900

.e.

•

Gra

vit

y

is

alw

a

ys

attrativ

e.

•

Einstein

's

answ

er:

to

a

v

oid

ollapse

(to

mak

e

the

univ

erse

stable)

it

is

neessary

to

in

tro-

due

a

form

of

repulsiv

e

gra

vit

y

,

b

y

mo

difying

the

equations

of

General

Relativit

y

.

0-3

Original

GR

equations

R

µν

−

1
2

Rg

µν

= 8πGT

µν

gravity

matter

T

ν

µ

=















ρ

0

0

0

0

−p

0

0

0

0

−p

0

0

0

0

−p















•

These

are

the

most

general

equations

that

are

1.

o

v

arian

t

2.

o

v

arian

tly

onserv

ed

3.

seond

order

in

the

metri

4.

reduing

to

Newton

at

lo

w

energy

0-4

Bo

x

on

T

µν

Basi

h

ydro

dynami

equations

for

a

NR

uid

at

rest:

˙ρ

= 0

(1)

∇p = 0

where

the

energy

densit

y

ρ = nmc

2

and

the

pres-

sure

is

p

i

= nmv

2

i

.

If

w

e

dene

the

matrix

T

µν

= diag(ρ, p, p, p)

then,

more

simply

T

µν

,µ

= 0

0-5

The

relativisti

v

ersion

is

the

only

tensor

that

de-

p

ends

on

ρ, p, u

µ

= dx

µ

/ds, g

µν

and

redues

to

this

limit

in

the

Mink

o

wski

spae

T

µν

= (ρ + p)u

µ

u

ν

− pg

µν

(2)

Einstein's

equations

are

omplete

only

when

a

re-

lation

b

et

w

een

p

and

ρ

is

giv

en:

the

equation

of

state.

0-6

Ba

k

to

R

µν

−

1
2

Rg

µν

= 8πGT

µν

•

F

or

instane,

negleting

the

third

ondition,

w

e

ould

add

whatev

er

rank-2

tensor

o

v

ari-

an

tly

onserv

ed,

e.g.

an

y

E

ν

µ

su

h

that

E

ν

µ;ν

= 0

•

lik

e

e.g.

a

linear

om

bination

of

RR

µν

, R

;µν

, R

2

g

µν

, ...

as

for

instane

[

F = F (R)

℄

E

µν

≡ F

′

R

µν

−

1
2

F g

µν

+ g

µν

F

′

− F

′

;µ;ν

obtaining

a

higher-order

gra

vit

y

.

0-7

•

Negleting

instead

the

fourth

ondition,

w

e

an

add

a

(smal

l

)

term

Λg

µν

and

rewrite

the

equations

as

R

µν

−

1
2

Rg

µν

− Λg

µν

= 8πGT

µν

•

The

new

term

is

the

osmologial

onstan

t

.

0-8

•

The

big

idea

of

the

latter

y

ears

has

b

een

to

mo

v

e

the

new

term

from

righ

t

to

left

R

µν

−

1
2

Rg

µν

= 8πGT

µν

+ Λg

µν

thereb

y

in

tro

duing

a

new

form

of

matter

T

µν(Λ)

=

Λ

8π

g

µν

•

This

matter

has

a

fundamen

tal

prop

ert

y

.

W

rit-

ing

T

ν

µ(Λ)

=

Λ

8π

δ

ν

µ

or















ρ

0

0

0

0

−p

0

0

0

0

−p

0

0

0

0

−p















=















Λ

8π

0

0

0

0

Λ

8π

0

0

0

0

Λ

8π

0

0

0

0

Λ

8π















0-9

one

gets

immediately

p

Λ

= −

Λ

8π

,

ρ

Λ

=

Λ

8π

that

is,

the

osmologial

onstan

t

has

nega-

tiv

e

pressure

(if

Λ > 0

).

•

In

tro

duing

the

equation

of

state

p = wρ

one

has

that

the

osmologial

onstan

t

has

a

negativ

e

eq.

of

state

w = −1

As

a

omparison,

the

eq.

of

state

of

matter

(dust

or

old

dark

matter)

is

p = mv

2

≈ 0 → w = 0

0-10

while

for

radiation

p = ρ/3 → w = 1/3

0-11

Bo

x

on

g

µν

What

is

the

metri

of

a

homo

gene

ous

and

isotr

opi

spae

?

Most

general

metri:

ds

2

= g

00

dt

2

+ 2g

0i

dx

i

dt − σ

ij

dx

i

dx

j

1)

isotrop

y

g

0i

= 0

2)

ridenition

of

time

dτ =

√

g

00

dt → g

00

= 1

so

that

ds

2

= dt

2

− σ

ij

dx

i

dx

j

0-12

Beause

of

isotrop

y

,

the

spatial

metri

ds

2

3

= σ

ij

dx

i

dx

j

an

dep

end

only

on

|r|

and

on

dx

2

+ dy

2

+ dz

2

=

dr

2

+ r

2

(dθ

2

+ sin

2

θdφ)

Then

ds

2

3

= a

2

(t)λ

2

(r)[dr

2

+ r

2

(dθ

2

+ sin

2

θdφ)]

or,

redening

r

,

ds

2

3

= a

2

(t)[λ

′2

(r

′

)dr

′2

+ r

′2

(dθ

2

+ sin

2

θdφ)]

(3)

so

w

e

are

left

with

a

single

unkno

wn

funtion

λ(r)

.

But

w

e

ha

v

e

still

to

imp

ose

homo

geneity

.

Ho

w?

Em

b

edding

a

3D

homogeneous

h

yp

ersphere

in

a

eulidean

4D

spae:

a

2

= x

2

1

+ x

2

2

+ x

2

3

+ x

2

4

(4)

4D

spherial

o

ordinates

x

1

= a cos χ sin θ sin φ

0-13

x

2

= a cos χ cos θ

x

3

= a cos χ sin θ cos φ

x

4

= a sin χ

Dieren

tiating

x

4

dx

4

= −(x

1

dx

1

+ x

2

dx

2

+ x

3

dx

3

)

w

e

get

ds

2

= dx

2

1

+ dx

2

2

+ dx

2

3

+ dx

2

4

= dx

2

1

+ dx

2

2

+ dx

2

3

+

(x

1

dx

1

+ x

2

dx

2

+ x

3

dx

3

)

2

x

2

4

= a

2

(dχ

2

+ sin

2

χ(dθ

2

+ sin

2

θdφ

2

))

whi

h

ho

w

that

sin χ = r

and

dχ = λdr

,

and

there-

fore

λ =

1

√

1 − r

2

0-14

There

is

another

p

ossibilit

y:

em

b

edding

a

3D

h

y-

p

erb

oli

spae

in

a

4D

eulidean

spae:

a

2

= x

2

1

+ x

2

2

+ x

2

3

+ kx

2

4

(5)

from

whi

h

ds

2

3

= a

2

(dχ

2

+ F (χ)(dθ

2

+ sin

2

θdφ

2

))

where

F (χ) =

sin χ

k = 1

χ

k = 0

sinh χ

k = −1

and

λ =

1

√

1 − kr

2

So

anlly

w

e

obtain

the

most

general

homo

genous

and

isotr

opi

metri

,

the

metri

of

F

riedmann-Rob

ertson-

0-15

W

alk

er

ds

2

= dt

2

−a

2

(t)[

dr

2

1 − kr

2

+r

2

(dθ

2

+sin

2

θdφ

2

)]

(6)

0-16

A

repulsiv

e

gra

vit

y

•

What

has

to

do

a

negativ

e

pressure

with

a

repulsiv

e

gra

vit

y

?

•

Homogeneous

and

isotropi

F

riedmann

met-

ri

ds

2

= dt

2

−a

2

dr

2

1 − kr

2

+ r

2

sin θdφ

2

+ r

2

dθ

2

F

or

a

single

p

erfet

uid,

the

ten

Einstein

equations

redue

to

t

w

o

equations

for

the

sale

fator

and

the

energy

densit

y

(here

w

e

put

for

simpliit

y

k = 0

and

alw

a

ys

assume

a

0

= 1

)

H

2

≡

˙a

a

2

=

8π

3

ρ

(7)

¨

a
a

= −

4π

3

(ρ + 3p) = −

4π

3

ρ(1 + 3w)

(8)

0-17

F

rom

the

seond

one

it

app

ears

that

if

w < −1/3

then

w

e

get

aelerated

expansion.

There-

fore

the

osmologial

onstan

t

(or

an

y

uid

with

w < −1/3

)

aelerates

the

expansion

→

repulsiv

e

gra

vit

y

.

W

e

all

this

h

yp

o-

thetial

uid

Dark

Ener

gy.

•

Consider

no

w

only

the

osm.

onstan

t

H

2

≡

˙a

a

2

=

8π

3

ρ

Λ

=

Λ

3

from

whi

h

a = a

0

e

√

Λ

3

t

This

aelerated

expansion

is

a

protot

yp

e

of

primordial

ination

(de

Sitter

metri).

0-18

•

Generally

sp

eaking,

there

are

at

least

three

omp

onen

ts

(plus

urv

ature)

so

that

dynam-

is

is

more

ompliate:

H

2

≡

˙a

a

2

=

8π

3

(ρ

γ

+ ρ

M

+ ρ

Λ

) −

k

a

2

˙ρ

i

+ 3H(ρ

i

+ p

i

) = 0

Ordinary

matter

(bary

ons

plus

dark

matter)

onserv

es

energy

during

expansion,

so

that

w

e

ha

v

e

three

dieren

t

b

eha

viors

ρ

γ

∼ a

−4

ρ

M

∼ a

−3

ρ

k

≡

k

a

2

∼ a

−2

ρ

Λ

∼ a

0

0-19

•

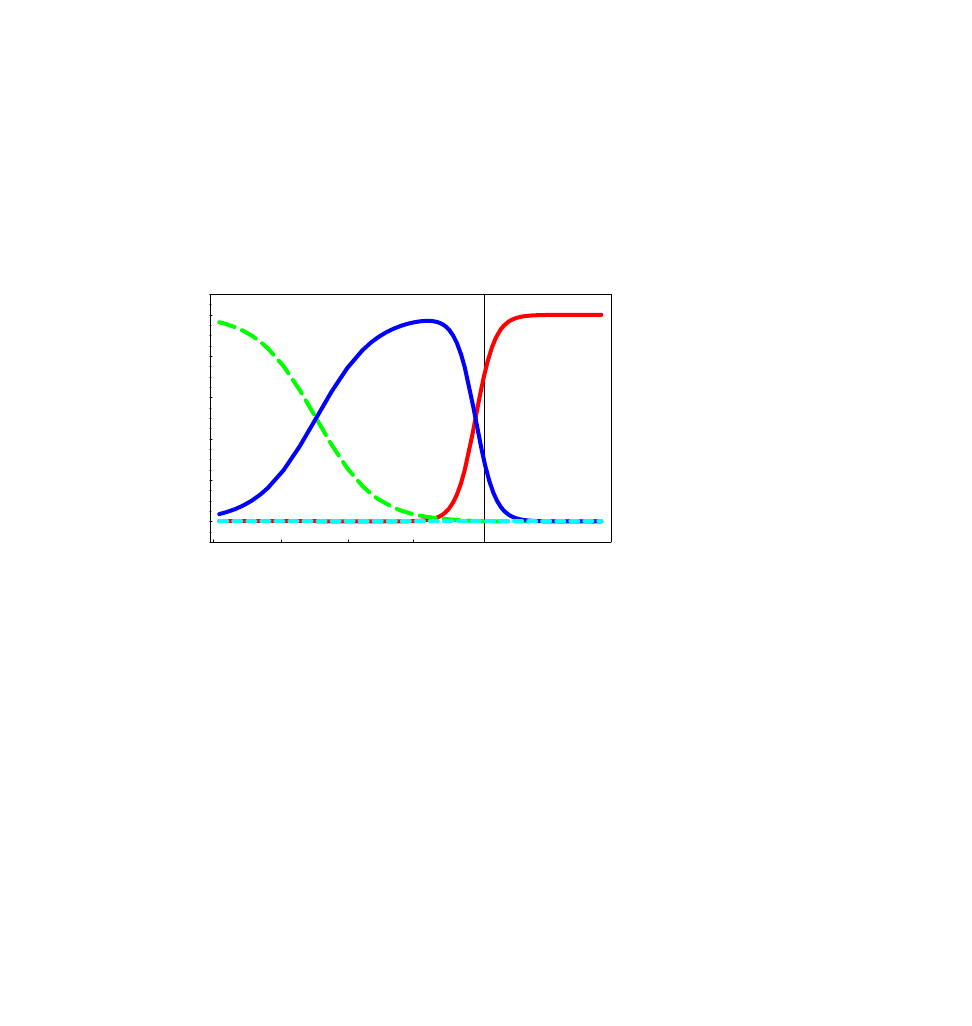
In

general,

therefore,

w

e

ha

v

e

rad. → matter → curvature → cosm.const.

10

0

10

1

10

2

10

3

10

4

1+z

0

0.2

0.4

0.6

0.8

1

W

Mat

Rad

L

0-20

Quan

tisti

in

terpretation

•

Think

of

a

eld,

eg

a

salar

eld,

as

a

series

of

lassial

osillators.

Then,

ev

ery

osillator

on

tributes

an

energy

due

to

the

sum

of

its

p

oten

tial

and

kineti

energy

.

•

When

at

rest,

ev

ery

osillator

has

only

its

p

oten

tial

energy

of

the

lo

w

est

lev

el,

that

w

e

an

alw

a

ys

put

to

zero.

•

Quan

tistially

,

ho

w

ev

er,

the

state

of

mini-

m

um

is

not

at

zero

energy

but

rather

E

0

=

1
2

~

ω

•

Therefore,

for

a

eld,

the

total

zero-p

oin

t

en-

0-21

ergy

is

E

0

=

X

i

1
2

~

ω

i

summing

o

v

er

all

p

ossible

mo

des.

Summing

o

v

er

k

i

= 2π/λ

i

where

λ

i

= L/n

i

are

all

the

w

a

v

elengths

of

the

mo

des

on

tained

in

a

b

o

x

of

size

L

,

w

e

obtain

dn

i

= dk

i

L/2π

mo

des

in

the

range

dk

i

,

so

that

E

0

=

1
2

~

L

3

Z

d

3

k

(2π)

3

ω

k

where

the

osillation

frequeny

is

in

relation

to

the

partile's

mass:

ω

2

= k

2

+ m

2

/~

2

The

total

energy

densit

y

in

tegrating

up

to

a

0-22

ut-o

frequeny

k

max

is

then

ρ

vacuum

= lim

E

L

3

= ~

k

4

max

16π

2

•

The

energy

div

erges

at

the

high

frequenies

(ultra

violet

div

ergene).

W

e

m

ust

supp

ose

then

that

there

is

k

max

b

ey

ond

whi

h

a

new

in

teration

mo

dies

the

system.

•

The

problem

is,

whi

h

k

max

?.

If

w

e

assume

as

limit

the

Plan

k

energy

E

P lanck

= 10

19

GeV

w

e

get

ρ

vacuum

= 10

92

g/cm

3

No

w,

the

exp

erimen

tal

limit

is

ρ = 3H

2

/8πG ≃ 10

−29

g/cm

3

0-23

then,

the

theoretial

estimate

is

o

b

y

120

orders

of

magnitude!

•

This

fundamen

tal

theoretial

problem

is

still

op

en

.

0-24

Astronom

y

of

Dark

Energy

•

W

e

ha

v

e

seen

that

the

F

riedmann

equation

has

the

form

H

2

=

8π

3

(ρ

M

+ ρ

Λ

+ ρ

k

+ ...?)

•

Supp

ose

w

e

kno

w

nothing

of

the

matter

on-

ten

t

of

the

univ

erse.

Ho

w

to

study

the

stru-

ture

of

the

osmos

?

0-25

•

Thr

e

e

levels

:

1.

ba

kground

eets

(age,

distanes)

2.

linear

p

erturbations

(gro

wth

of

lustering,

CMB)

3.

non-linear

p

erturbations

(formation

of

ol-

lapsed

ob

jets,

halo

proles).

0-26

Notie

that

a

smo

oth

omp

onen

t,

as

the

Λ

,

has

no

lo

al

observ

ational

eets:

The

P

oisson

equa-

tion

remains

in

v

aried,

b

eause

in

linear

GR

the

P

oisson

equation

△Ψ = −4πGρ

b

eomes

△Ψ = −4πGδρ

That's

wh

y

w

e

need

osmology

!

0-27

F

rom

observ

ations

to

theory

•

What

w

e

really

observ

e

in

osmology

is

ligh

t

from

soures

and

from

ba

kgrounds

.

•

Ho

w

do

w

e

onnet

these

observ

ables

to

os-

mologial

quan

tities

lik

e

ρ

m

, ρ

γ

, k, a(t), H

0

et?

•

First,

dene

Ω

M

=

8πρ

0

3H

2

0

,

Ω

Λ

=

8πρ

Λ

3H

2

0

,

Ω

k

=

8πk

3H

2

0

and

note

that

1 = Ω

M

+ Ω

Λ

+ Ω

k

so

rewrite

F

riedman

equation

as

(

a

0

= 1

)

H

2

= H

2

0

(Ω

m

a

−3

+ Ω

Λ

a

0

+ Ω

k

a

−2

)

0-28

•

Then,

generalize

it

to

sev

eral

omp

onen

ts:

H

2

= H

2

0

(Ω

m

a

−3(1+w

m

)

+ Ω

Λ

a

−3(1+w

Λ

)

+ ...)

= H

2

0

X

i

Ω

i

a

−3(1+w

i

)

= H

2

0

E(a)

2

•

F

or

instane...

name

densit

y

Ω

i

state

w

i

bary

ons

0.05

0

CDM

0.3

0

radiation

0.0001

1/3

osm.

onst.

0.7

-1

urv

ature

<0.03

-1/3

other

?

?

?

0-29

•

Unkno

wn

quan

tities:

H

0

, Ω

i

, w

i

to

b

e

deter-

mined

using:

1.

Angular

p

ositions

of

soures,

e.g.

galaxies:

θ

i

, ϕ

i

2.

Redshifts:

z

i

3.

Apparen

t

magnitudes:

m

i

4.

Ages

of

stars

5.

Ba

kground

radiation

e.g.

CMB:

∆T /T

•

BASIC

RELA

TION

redshift/sale

fator:

a =

1

1+z

0-30

First

basi

observ

able:

Age

of

the

Univ

erse

•

The

age

of

the

univ

erse

an

b

e

dedued

from

the

F

riedmann

equation:

da

dt

2

= H

2

0

a

2

E(a)

2

w

e

get

dz

H

0

dt

= (1 + z)E(z)

and

nally

t

0

− t

1

= H

−1

0

Z

z

1

0

dz

(1 + z)E(z)

0-31

Notie

that

the

Hubble

onstan

t

is

H

−1

0

=

1

100hkm/sec/M pc

= 9.76h

−1

Gyr

F

or

z

1

→ ∞

w

e

get

then

the

age

of

the

uni-

v

erse.

•

The

eet

of

the

osmologial

onstan

t

,

when

Ω

tot

= Ω

M

+ Ω

Λ

is

xed,

is

to

inrease

the

osmologial

age.

0-32

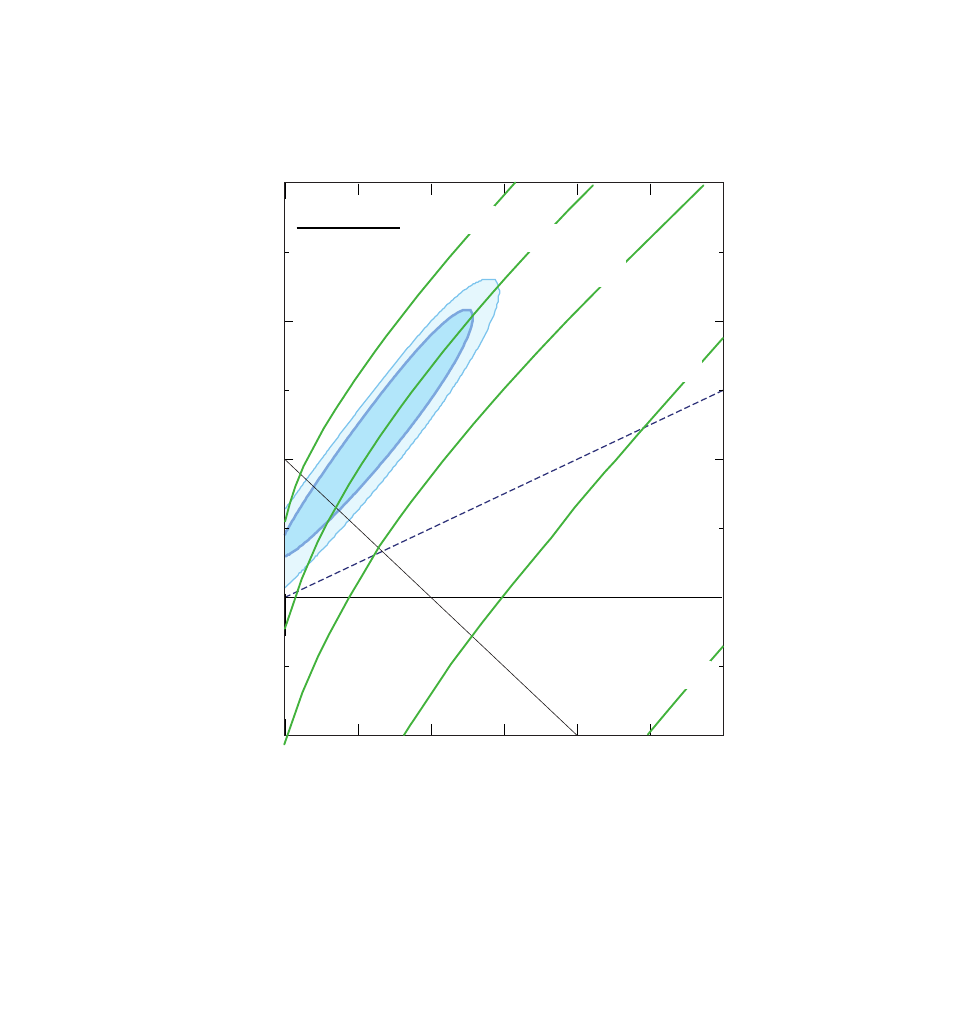
Ω

Μ

1

2

0

1

2

3

Ω

Λ

-1

0

1

2

3

2

3

Supernova Cosmology Project

Perlmutter et al. (1998)

Best fit age of universe:

t

o

= 14.5

±

1 (0.63/h) Gyr

Best fit in flat universe:

t

o

= 14.9

±

1 (0.63/h) Gyr

19 Gyr

14.3 Gyr

accelerating

decelerating

11.9 Gyr

9.5 Gyr

7.6 Gyr

H

0

t

0

63 km s

-1

Mpc

-1

=

0-33

Seond

basi

observ

able:

Luminosit

y

distane

•

F

rom

at

F

riedmann's

metri

ds

2

= c

2

dt

2

− a

2

dr

2

and

in

tegrating

along

the

n

ull

geo

desis,

w

e

get

the

prop

er

distane

whi

h

is

what

y

ou

w

ould

measure

with

xed

ro

ds

r =

Z

cdt

a(t)

= c

Z

da

˙aa

= c

Z

dz

H(z)

→

generalized

Hubble

la

w

:

measuring

dis-

tanes

means

measuring

osmology.

•

If

w

e

ompare

the

energy

L

emitted

b

y

a

soure

at

prop

er

distane

r

with

ux

f

arriv-

ing

at

the

observ

er,

w

e

dene

the

luminosit

y

0-34

distane

d(z)

su

h

that

f =

L

4πr

2

(1 + z)

2

=

L

4πd

2

•

The

t

w

o

extra

fators

of

1 + z

tak

e

in

to

a-

oun

t

the

loss

of

energy

due

to

redshift

and

the

spread

of

energy

due

to

the

relativ

e

di-

latation

of

the

emission

time

v

ersus

observ

er's

time.

W

e

get

d(z) = r(1 + z) = cH

−1

0

(1 + z)

Z

z

1

0

dz

E(z)

where

cH

−1

0

=

300.000km/sec

100hkm/sec/M pc

= 3000h

−1

M pc

.

•

Remem

b

er

our

referene

osmology

E

2

(z) = Ω

M

(1 + z)

3

+ Ω

Λ

+ Ω

K

(1 + z)

2

0-35

•

The

luminosit

y

distane

therefore

dep

ends

up

on

the

osmologial

onstan

t

and,

lik

e

for

the

age,

inreases

for

Ω

Λ

inreasing.

Therefore,

a

larger

osm.

onst.

indues

a

smaller

lu-

minosit

y

of

the

standard

andles.

•

Supp

ose

w

e

ha

v

e

a

soure

of

kno

wn

absolute

luminosit

y

M = −2.5 log L + const

.

Then

one

denes

instead

of

the

ux

f

an

apparen

t

magnitude

m = −2.5 log f + const

as

m − M = 25 + 5 log d(z; Ω

M

, Ω

Λ

)

If

M

is

the

same

for

ev

ery

ob

jet,

then

the

apparen

t

magnitude

giv

es

diretly

d(z)

and

is

then

p

ossible

to

test

for

the

presene

of

a

osmologial

onstan

t.

0-36

0.2

0.4

0.6

0.8

W

M

0.2

0.4

0.6

0.8

W

L

z=10

0.2

0.4

0.6

0.8

W

M

0.2

0.4

0.6

0.8

W

L

z=1000

0.2

0.4

0.6

0.8

W

M

0.2

0.4

0.6

0.8

W

L

z=0.7

0.2

0.4

0.6

0.8

W

M

0.2

0.4

0.6

0.8

W

L

z=4

Figure

1:

Curv

es

of

onstan

t

d(z; Ω

M

, Ω

Λ

)

.

0-37

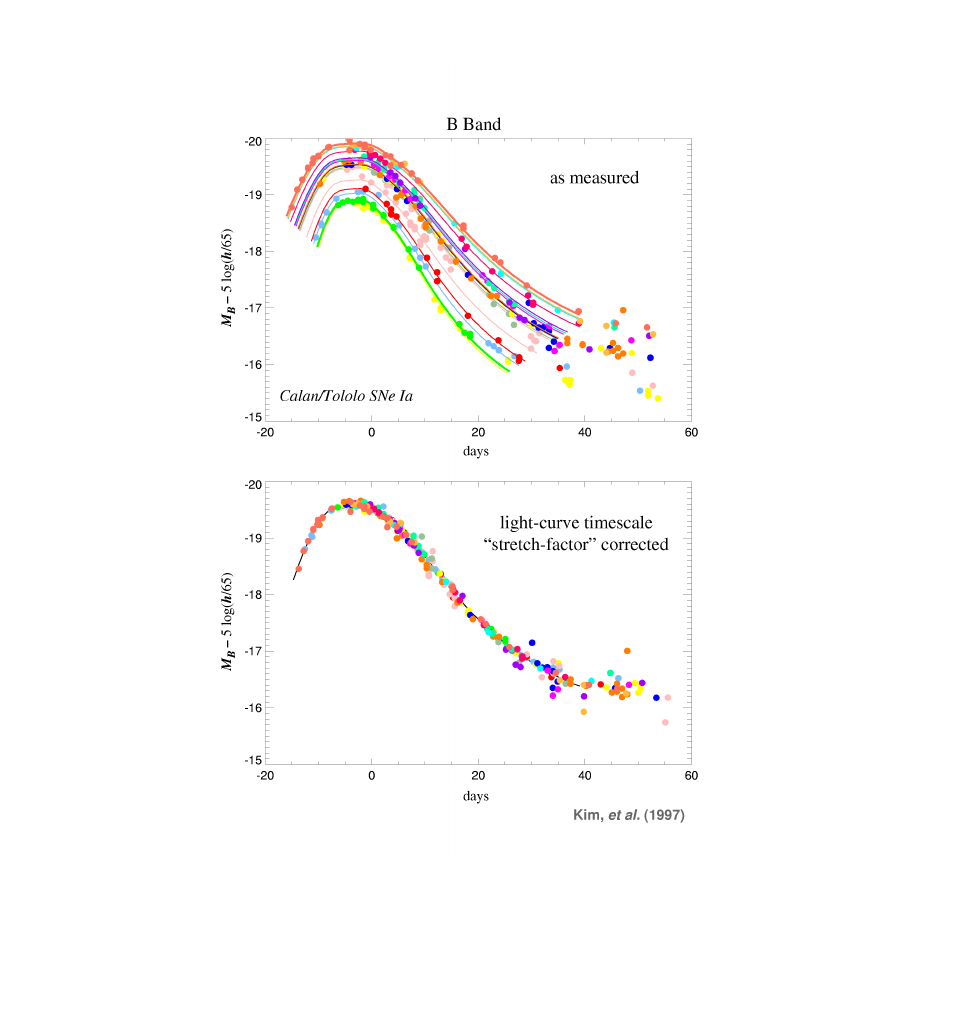
Standard

andles

•

There

exist

standard

andles

in

nature

?

•

The

b

est

su

h

thing

so

far

are

sup

erno

v

ae

Ia

.

0-38

0-39

•

This

h

yp

othesis

an

b

e

tested

and

alibrated

through

a

lo

al

sample

whose

distane

w

e

kno

w

b

y

other

means.

0-40

0-41

•

Then,

w

e

ompare

m

obs

(z)

with

m

theor

(z) = M + 25 + log d(z; Ω

M

, Ω

Λ

, ..)

•

F

or

instane

z = 1,

M = −19.5

Ω

M

= 0,

Ω

Λ

= 1

Ω

M

= 1,

Ω

Λ

= 0

,

m

theor

= 24.4

m

theor

= 23.2

More

than

t

wie

as

brigh

ter

!

0-42