
1
Aproksymacja funkcji
Wykład szósty
EiT, sem. 2, 2014/2015

2
Aproksymacja
oznacza przybliżanie.
W matematyce aproksymacja oznacza
zastąpienie funkcji aproksymowanej
funkcją aproksymująca z reguły funkcją o prostszej postaci.
Funkcja
aproksymująca powinna być określona na tym samym zbiorze
argumentów, co funkcja aproksymowana.
Wykonanie aproksymacji wymaga określenia:
- funkcji aproksymowanej y = f(x)
– często funkcja dyskretna,
-
zbioru funkcji, z których wybieramy funkcję aproksymującą y = F(x),
-
kryterium oceny jakość aproksymacji.

Przybliżanie określonej funkcji, funkcji aproksymowanej, inną funkcją,
f
unkcją aproksymującą, powoduje powstanie błędów. Są to błędy aproksymacji.
Błędy aproksymacji przedstawiane są w postaci funkcji błędu.
Przybliżanie funkcji aproksymowanej jest zwykle wykonywane przy zastosowaniu
określonego kryterium jakości aproksymacji, zwykle minimalizacji funkcji błędu.
Kryterium określające jakość aproksymacji
Jest to warunek osiągnięcia wartości minimalnej przez funkcję błędu,
która jest zależna od funkcji aproksymowanej i aproksymującej.
Do często stosowanych metod aproksymacji należą:
aproksymacja jednostajna,
aproksymacja średniokwadratowa.
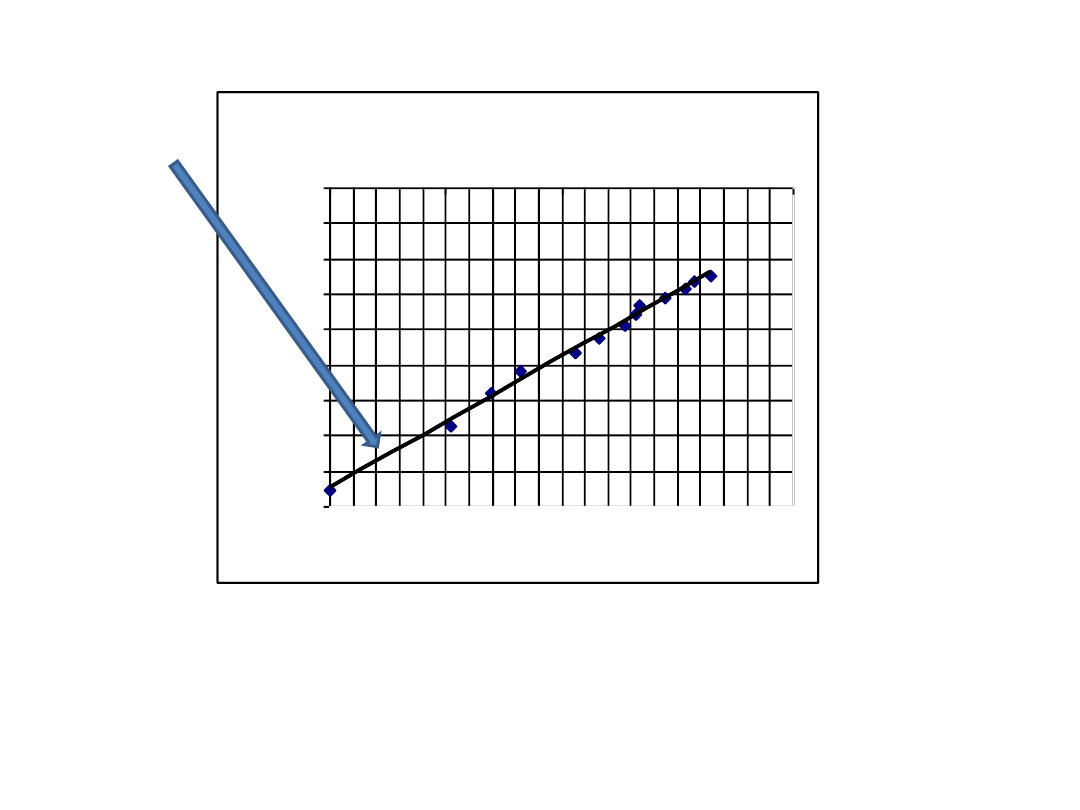
y = 0,4643x - 4,246
-4,5
-4
-3,5
-3
-2,5
-2
-1,5
-1
-0,5
0
0
2
4
6
8
lnt
Y*
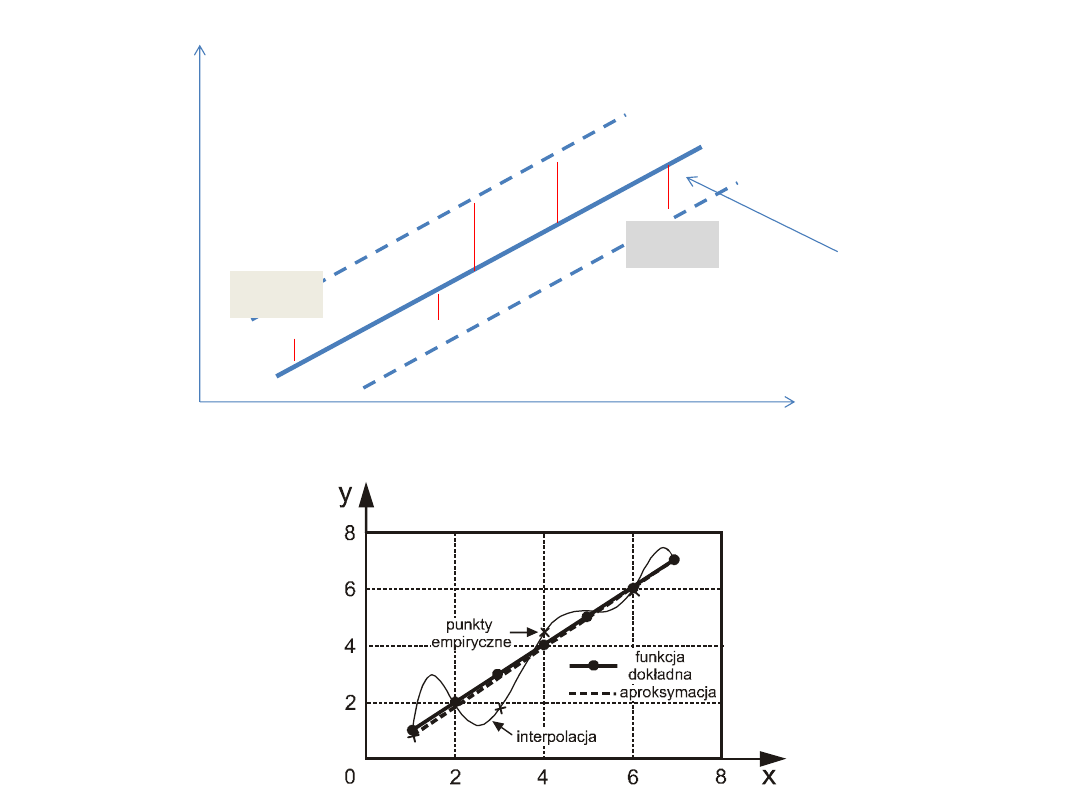
Przykład aproksymacji
Aproksymacja polega na „dopasowaniu” funkcji aproksymującej do funkcji
a
proksymowanej, tak aby błąd przybliżenia był minimalny.
Funkcja aproksymująca może, ale nie musi, przechodzić przez punkty
y
i
= f(x
i
), i = 1, 2, …, n, czyli przez funkcję aproksymowaną.
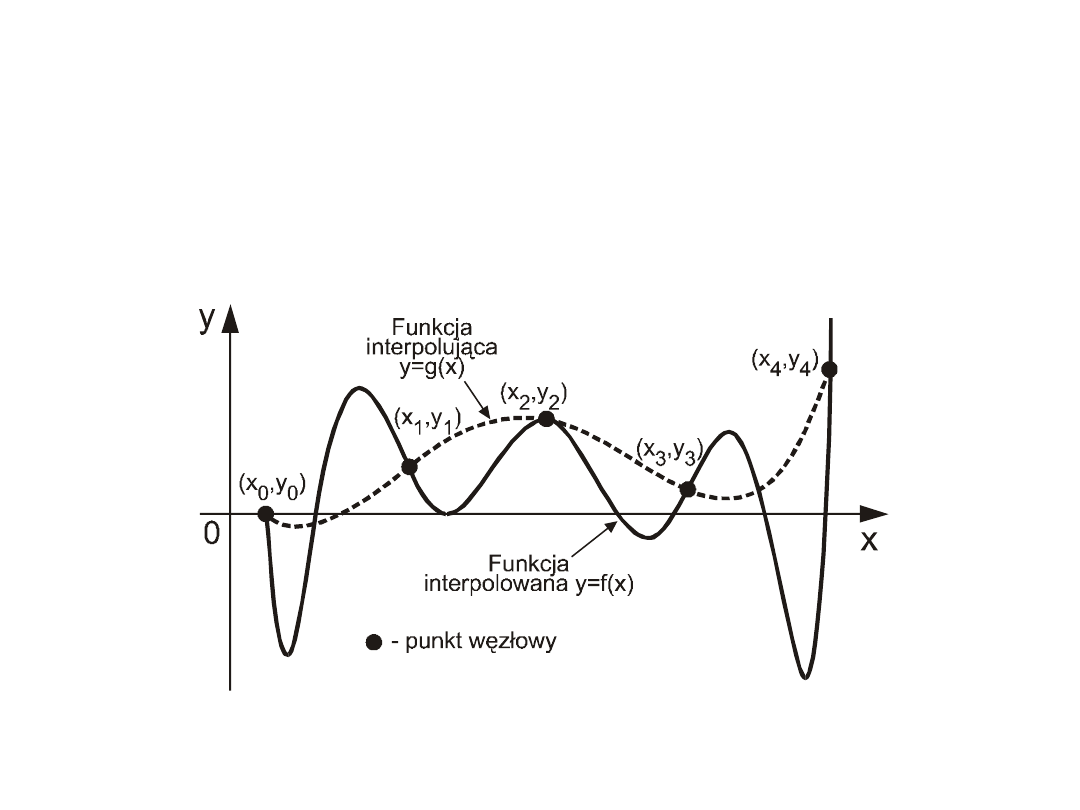
Funkcja aproksymująca

Interpolacja
6
Interpolacja
jest szczególnym przypadkiem aproksymacji.
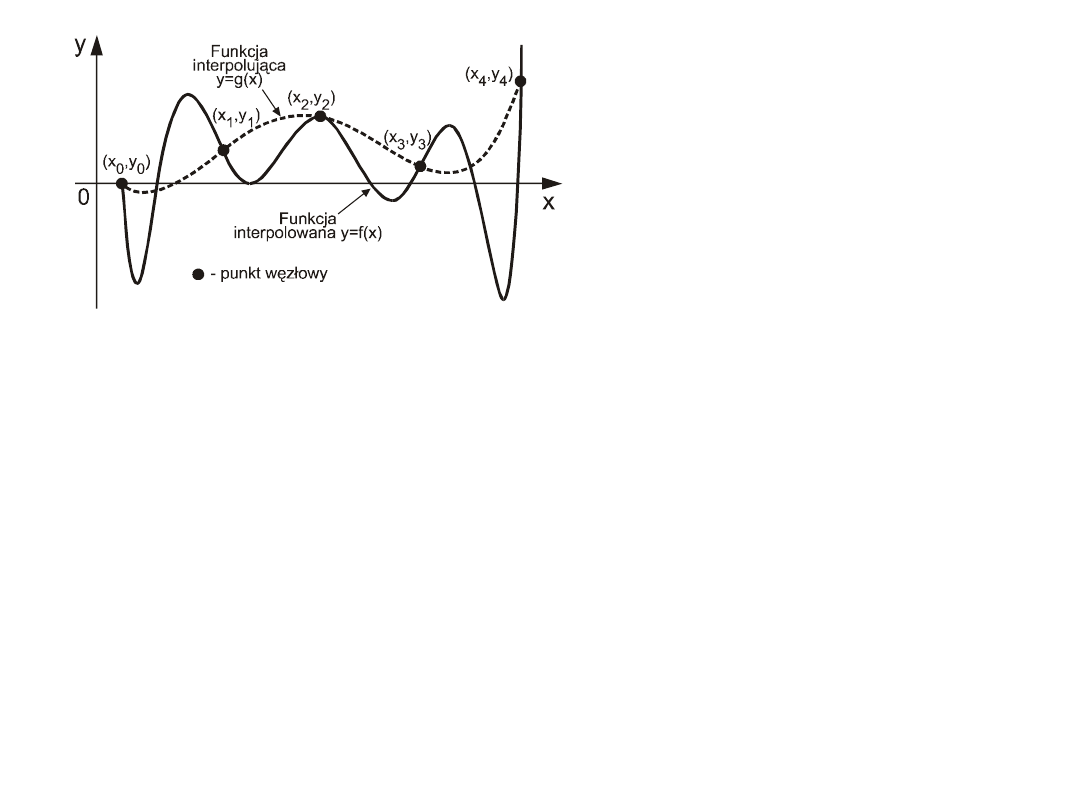
Interpolacja
7
Dane są to wartości funkcji f (x)
zapisane jako
n
i
x
f
y
i
i
,...,
2
,
1
,
0
)
(
Należy znaleźć funkcję g (x) określonej klasy, która przyjmuje w węzłach
interpolacji te same wartości co funkcja interpolowana
n
i
x
f
y
i
i
,...,
2
,
1
,
0
)
(
n
i
y
x
g
i
i
...,
,
1
,
0
)
(
czyli
Interpolacja:
odcinkami, wielomianami potęgowymi Lagrange’a, wielomianami
Newtona, różnicami skończonymi, funkcjami sklejanymi

8
Interpolacja wielomianami Lagrange’a
Należy znaleźć dla danej funkcji f (·) taki wielomian potęgowy stopnia nie wyższego niż
n oznaczanego przez
)
(
n
L
którego wartości w n + 1 zadanych punktach
n
i
x
y
i
i
...,
,
1
,
0
,
,
są równe odpowiednim wartościom funkcji, co oznacza, że
n
i
dla
x
f
x
L
i
i
n
...,
,
1
,
0
)
(
)
(
n
i
x
y
i
i
...,
,
1
,
0
,
,
Punkty
węzły interpolacji
9
Wielomiany Lagrange’a
)
(
)
(
)
(
0
x
L
y
x
L
n
i
n
i
i
n
)
)...(
)(
)...(
)(
(
)
)...(
)(
)....(
)(
(
)
(
1
1
1
0
1
1
1
0
)
(
n
i
i
i
i
i
i
i
n
i
i
n
i
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
L
Dla n = 2 i = 0, 1, 2 mamy
)
)(
(
)
)(
(
)
(
2
0
1
0
2
1
)
2
(
0
x
x
x
x
x
x
x
x
x
L
)
)(
(
)
)(
(
)
(
2
1
0
1
2
0
)
2
(
1
x
x
x
x
x
x
x
x
x
L
)
)(
(
)
)(
(
)
(
1
2
0
2
1
0
)
2
(
2
x
x
x
x
x
x
x
x
x
L
10
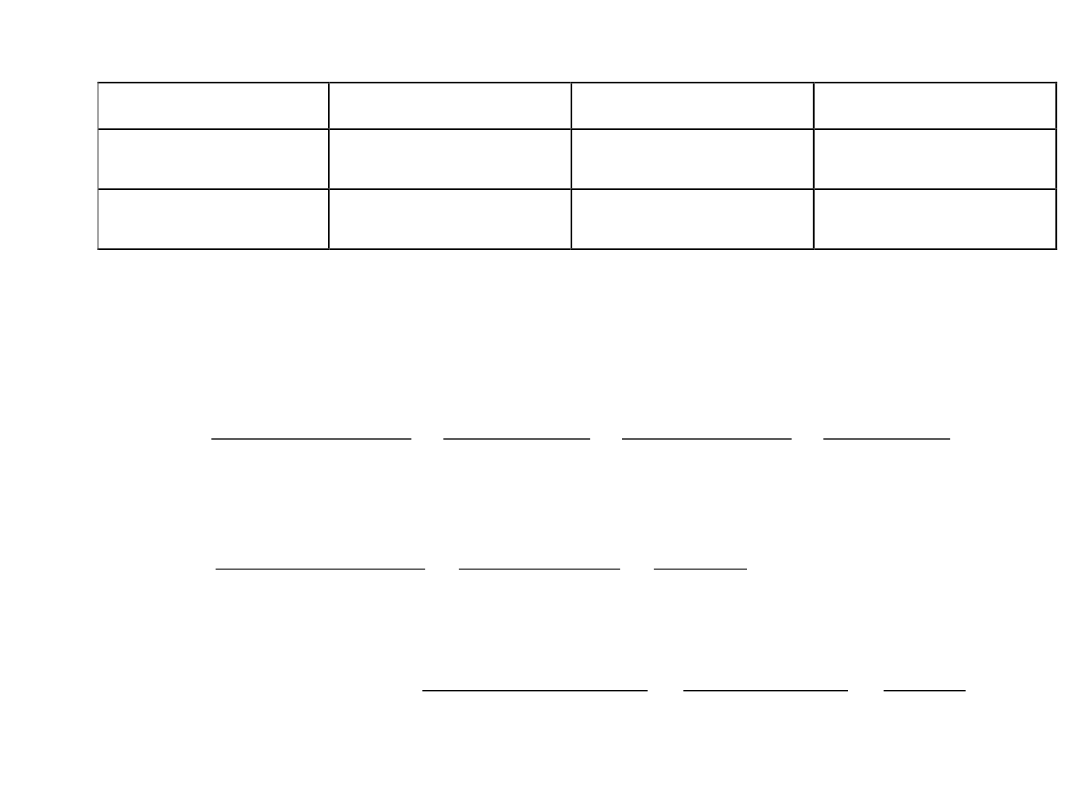
Przykład
Dane
i
0
1
2
i
x
0
1
2
i
y
-1
0
3
)
(
)
(
)
(
)
(
)
(
)
2
(
2
2
)
2
(
1
1
)
2
(
0
0
2
2
0
2
x
L
y
x
L
y
x
L
y
x
L
y
x
L
i
i
i
2
2
3
2
2
2
)
2
0
)(
1
0
(
)
2
)(
1
(
)
)(
(
)
)(
(
)
(
2
2
2
0
1
0
2
1
)
2
(
0
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
L
1
2
)
2
1
)(
0
1
(
)
2
)(
0
(
)
)(
(
)
)(
(
)
(
2
2
1
0
1
2
0
)
2
(
1
x
x
x
x
x
x
x
x
x
x
x
x
x
L
2
)
1
2
)(
0
2
(
)
1
)(
0
(
)
)(
(
)
)(
(
)
(
2
1
2
0
2
1
0
)
2
(
2
x
x
x
x
x
x
x
x
x
x
x
x
x
L
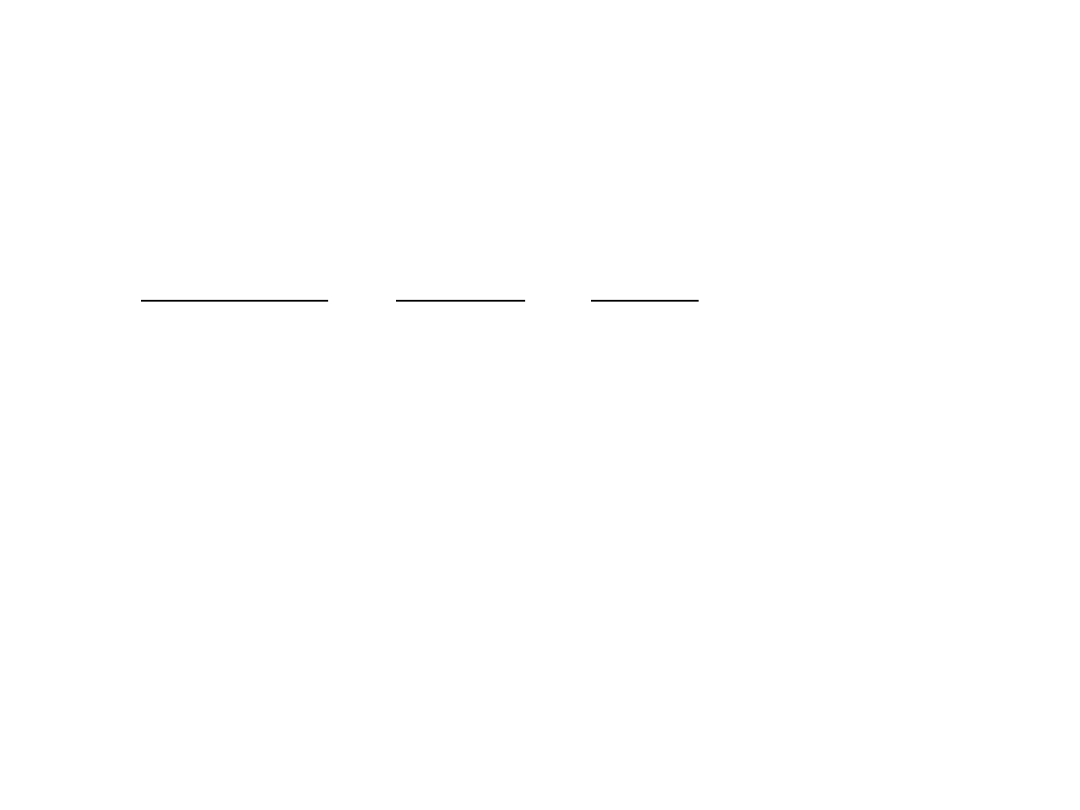
11
1
2
3
1
2
0
2
2
3
)
1
(
)
(
)
(
)
(
)
(
)
(
2
2
2
2
)
2
(
2
2
)
2
(
1
1
)
2
(
0
0
2
2
0
2
x
x
x
x
x
x
x
x
L
y
x
L
y
x
L
y
x
L
y
x
L
i
i
i
Sprawdzenie
3
2
0
1
1
0
2
2
1
1
0
0
y
x
y
x
y
x
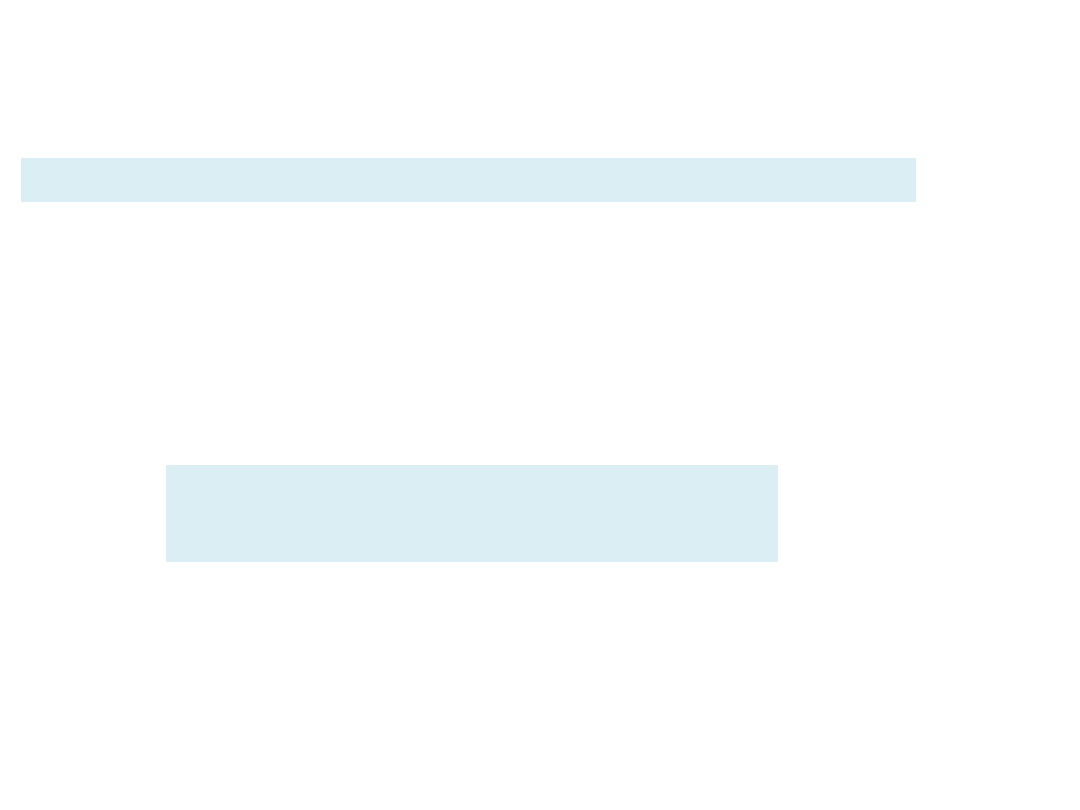
12
Interpolacja wzorami Newtona
– pierwszy wzór interpolacyjny Newtona
Pierwszy wzór interpolacyjny Newtona ma postać:
)
)...(
(
)
(
...
)
(
)
(
)
(
)
(
1
1
0
1
0
2
0
1
0
n
n
x
x
x
x
x
x
a
x
x
x
x
a
x
x
a
a
x
P
Należy wyznaczyć współczynniki
n
a
a
a
a
,....,
,
,
2
1
0

13
n
n
n
n
n
n
n
n
n
o
y
x
x
x
x
x
x
a
x
x
x
x
a
x
x
a
a
y
x
x
x
x
a
x
x
a
a
y
x
x
a
a
y
a
)
)...(
)(
(
...
)
)(
(
)
(
....
...
)
)(
(
)
(
)
(
1
1
0
1
0
2
1
1
0
2
1
2
0
2
2
0
2
1
0
1
0
1
1
0
0
Współczynniki
n
a
a
a
a
,....,
,
,
2
1
0
wyznacza się przez rozwiązanie układu równań
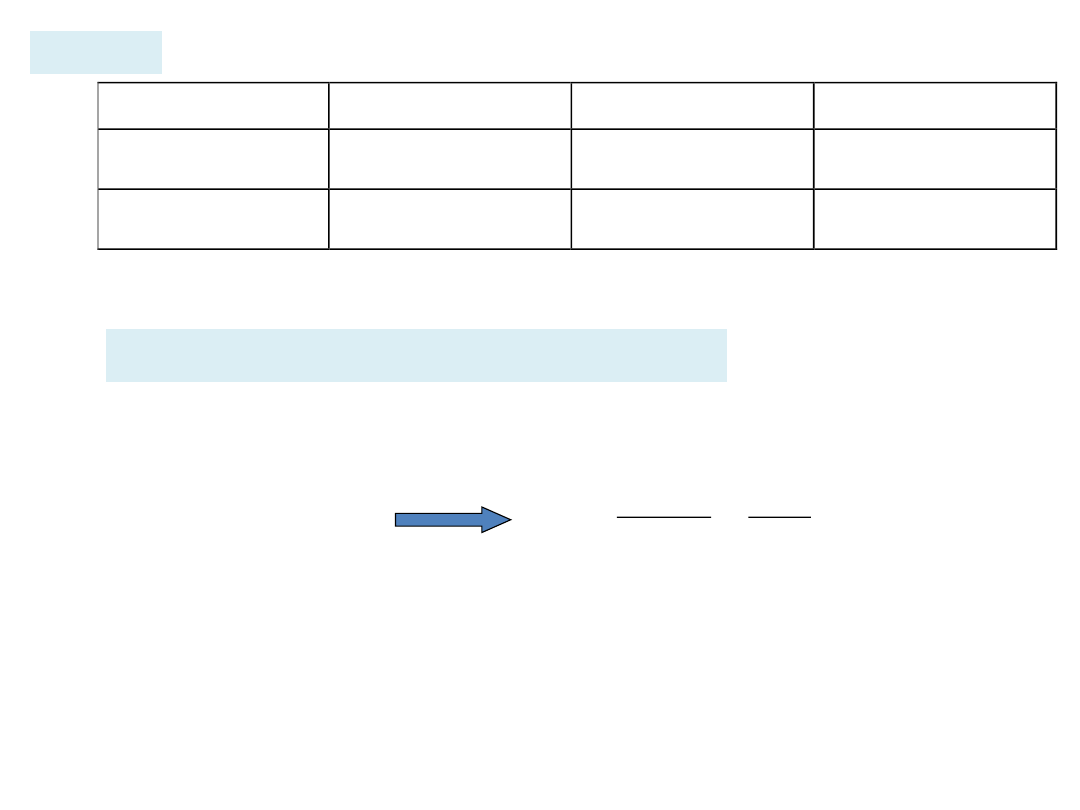
14
Przykład
Dane
i
0
1
2
i
x
0
1
2
i
y
-1
0
3
)
(
)
(
)
(
)
(
1
0
2
0
1
0
x
x
x
x
a
x
x
a
a
x
P
1
0
1
1
0
0
)
(
1
y
x
x
a
a
y
a
o
1
0
1
1
0
0
1
0
1
1
x
x
a
y
a
2
1
2
0
2
2
0
2
1
0
)
)(
(
)
(
y
x
x
x
x
a
x
x
a
a

15
2
1
2
0
2
2
0
2
1
0
)
)(
(
)
(
y
x
x
x
x
a
x
x
a
a
3
)
1
2
)(
0
2
(
)
0
2
(
1
1
2
a
1
2
a
1
1
)
1
)(
0
(
1
)
0
(
1
1
)
(
)
(
)
(
)
(
2
2
1
0
2
0
1
0
x
x
x
x
x
x
x
x
x
x
x
a
x
x
a
a
x
P
1
)
(
2
x
x
P
Należy sprawdzić, czy wielomian P(x) przybiera wartości zadane

16
Aproksymacja funkcji na podzbiorze
dyskretnym metodą najmniejszych kwadratów

17
Zakładamy, że znane są wartości
n
i
x
f
y
i
i
,
,
2
,
1
,
0
,
funkcji f (
·) dla dyskretnych wartości argumentu równych
b
x
x
x
a
x
n
2
1
0

18
Będziemy poszukiwać funkcji aproksymującej
x
y
w postaci
x
c
x
c
x
c
x
m
m
1
1
0
0
gdzie:
m
,
,
,
1
0
są pewnymi funkcjami określonymi na danym przedziale [a, b],
m
c
c
c
,
,
,
1
0
są współczynnikami będącymi liczbami rzeczywistymi.
Wielomian uogólniony

19
Jakość aproksymacji
Kryterium określające jakość aproksymacji – funkcja błędu F(·) definiująca
odległość pomiędzy funkcjami f (·) i Φ (·) na danym zbiorze
n
x
x
x
,
,
,
1
0
Z
z zakresu [a, b].
Przez
,
f
F
oznaczono wartość funkcji błędu
W
metodzie najmniejszych kwadratów, przy aproksymacji na podzbiorze dyskretnym,
funkcję błędu definiuje się jako:
2
/
1
2
0
0
,
n
i
m
k
i
k
k
i
i
def
x
c
x
f
x
w
f
f
F
Z
norma wyznaczana na podzbiorze dyskretnym Z
funkcja wagowa
20
x
y
*
*
*
*
*
Funkcja aproksymująca
𝑦
1
, 𝑥
1
𝑦
𝑛
, 𝑥
𝑛

21
Poszukujemy współczynników
m
c
c
c
,
,
,
1
0
dla których funkcja
2
/
1
2
0
0
,
n
i
m
k
i
k
k
i
i
def
x
c
x
f
x
w
f
f
F
Z
przyjmuje wartość minimalną.
Funkcje bazowe
m
,
,
,
1
0
są dane.
2
0
0
n
i
m
k
i
k
k
i
x
c
x
f

22
Otrzymujemy m
+1 równań
,
,
,
2
,
1
,
0
dla
,
0
m
k
dc
d
k
z m +1 niewiadomymi
m
c
c
c
,
,
,
1
0
Po zróżniczkowaniu funkcji
n
i
m
l
i
l
l
i
i
k
k
x
c
x
f
x
dc
d
0
0
2
m
k
,
,
2
,
1
,
0
2
0
0
n
i
m
k
i
k
k
i
x
c
x
f
otrzymujemy:

23
Układ równań przyjmuje postać:
0
0
0
m
l
i
l
l
i
n
i
i
k
x
c
x
f
x
gdzie:
m
k
,
,
2
,
1
,
0
a po przekształceniu:
n
i
i
i
k
m
l
i
l
l
n
i
i
k
x
f
x
x
c
x
0
0
0
m
k
,
,
2
,
1
,
0

24
Do obliczeń stosujemy następującą formę układu równań:
n
i
i
i
k
l
m
l
n
i
i
l
i
k
x
f
x
c
x
x
0
0
0
m
k
,
,
2
,
1
,
0
kl
s
S
Oznaczając macierz współczynników układu przez
m
l
k
x
x
s
n
i
i
l
i
k
kl
,
,
1
,
0
,
,
0

25
Wektor wyrazów wolnych oznaczymy przez
T
m
t
t
t
,
,
,
1
0
t
Możemy układ m+1 równań z m+1 niewiadomymi
zapisać jako
m
c
c
c
,
,
,
1
0
t
c
S
m
k
x
f
x
t
n
i
i
i
k
k
,
,
1
,
0
,
0
Jest to układ równań nazywany układem równań normalnych

26
Funkcje bazowe
przyjmuje się jako ciąg wielomianów
,
,
,
,
1
0
k
,
,
,
,
,
1
2
0
k
x
x
x
x
Jako funkcje aproksymujące stosujemy wielomian potęgowy
m
m
x
c
x
c
x
c
c
x
2
2
1
0
Wtedy
n
i
l
k
i
kl
m
l
k
x
s
0
,
,
2
,
1
,
0
,
,
n
i
i
k
i
k
m
k
x
f
x
t
0
,
,
2
,
1
,
0
,

27
Przyjęto oznaczenie
kl
j
s
s
gdzie j = k + l
Układ równań możemy zapisać:
m
m
m
m
m
m
m
m
m
m
m
m
t
c
s
c
s
c
s
c
s
t
c
s
c
s
c
s
c
s
t
c
s
c
s
c
s
c
s
t
c
s
c
s
c
s
c
s
2
2
2
1
1
0
2
2
2
4
1
3
0
2
1
1
2
3
1
2
0
1
0
2
2
1
1
0
0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
gdzie
n
i
j
i
j
m
j
x
s
0
2
,
,
2
,
1
,
0
dla
,

28
Dla m
= 1 mamy wyrażenia:
n
i
i
n
i
i
n
i
i
x
s
x
s
x
s
0
2
2
0
1
1
0
0
0
n
i
i
i
n
i
i
i
y
x
t
y
x
t
0
1
1
0
0
0
Dla m
= 2 mamy wyrażenia:
n
i
i
i
n
i
i
i
n
i
i
i
y
x
t
y
x
t
y
x
t
0
2
2
0
1
1
0
0
0
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
x
s
x
s
x
s
x
s
x
s
0
4
4
0
3
3
0
2
2
0
1
1
0
0
0
29
Przykład
i
0
1
2
i
x
0
1
2
i
y
-1
0
3
m = 2
17
2
1
0
9
2
1
0
5
2
1
0
3
2
1
0
3
2
1
0
4
4
4
0
4
4
3
3
3
0
3
3
2
2
0
2
2
2
1
1
1
0
1
1
0
0
0
0
0
0
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
x
s
x
s
x
s
x
s
x
s
12
)
3
(
2
)
0
(
1
)
1
(
0
6
)
3
(
2
)
0
(
1
)
1
(
0
2
)
3
(
2
)
0
(
1
)
1
(
0
2
2
2
0
2
2
1
1
1
0
1
1
0
0
0
0
0
0
n
i
i
i
n
i
i
i
n
i
i
i
y
x
t
y
x
t
y
x
t

30
2
2
1
0
)
(
x
c
x
c
c
x
2
2
4
1
3
0
2
1
2
3
1
2
0
1
0
2
2
1
1
0
0
t
c
s
c
s
c
s
t
c
s
c
s
c
s
t
c
s
c
s
c
s
2
1
0
,
,
c
c
c
12
17
9
5
6
9
5
3
2
5
3
3
2
1
0
2
1
0
2
1
0
c
c
c
c
c
c
c
c
c
wynik
1
,
0
,
1
2
1
0
c
c
c
1
1
0
1
)
(
2
2
2
2
1
0
x
x
x
x
c
x
c
c
x

31
Wyszukiwarka
Podobne podstrony:
Czwarty wykład 2014 bez tła
Pierwszy wyklad 2014 bez tła
Drugi wykład 2014 bez tła
Czwarty wykład 2014 bez tła
Czwarty wykład cd 2014 bez tła
wykład z cholestazy (bez zdjęć)
MOO wyklad 2 ekstrema bez ograniczen
Pestycydy wykłady 2014
podstawy rachunkowosci we dzienne wyklad 2014
ppmy wyklad 2014 KasiaB
ANTROPOLOGIA NOTATKI Z WYKŁADÓW (2014)
Rezerwa z tytułu odrocznego podatku - materiały do wykładu 2014, UE KATOWICE ROND, I stopień, VI sem
Rezerwy na świadczenia pracownicze - materiały do wykladu 2014, UE KATOWICE ROND, I stopień, VI seme
4 Stres Wyklad 4 2014
ćw 4 [ genom chloroplastowy ] bez tła
Problemy zdrowia w skali międzynarodowej wykład 2 2014
więcej podobnych podstron