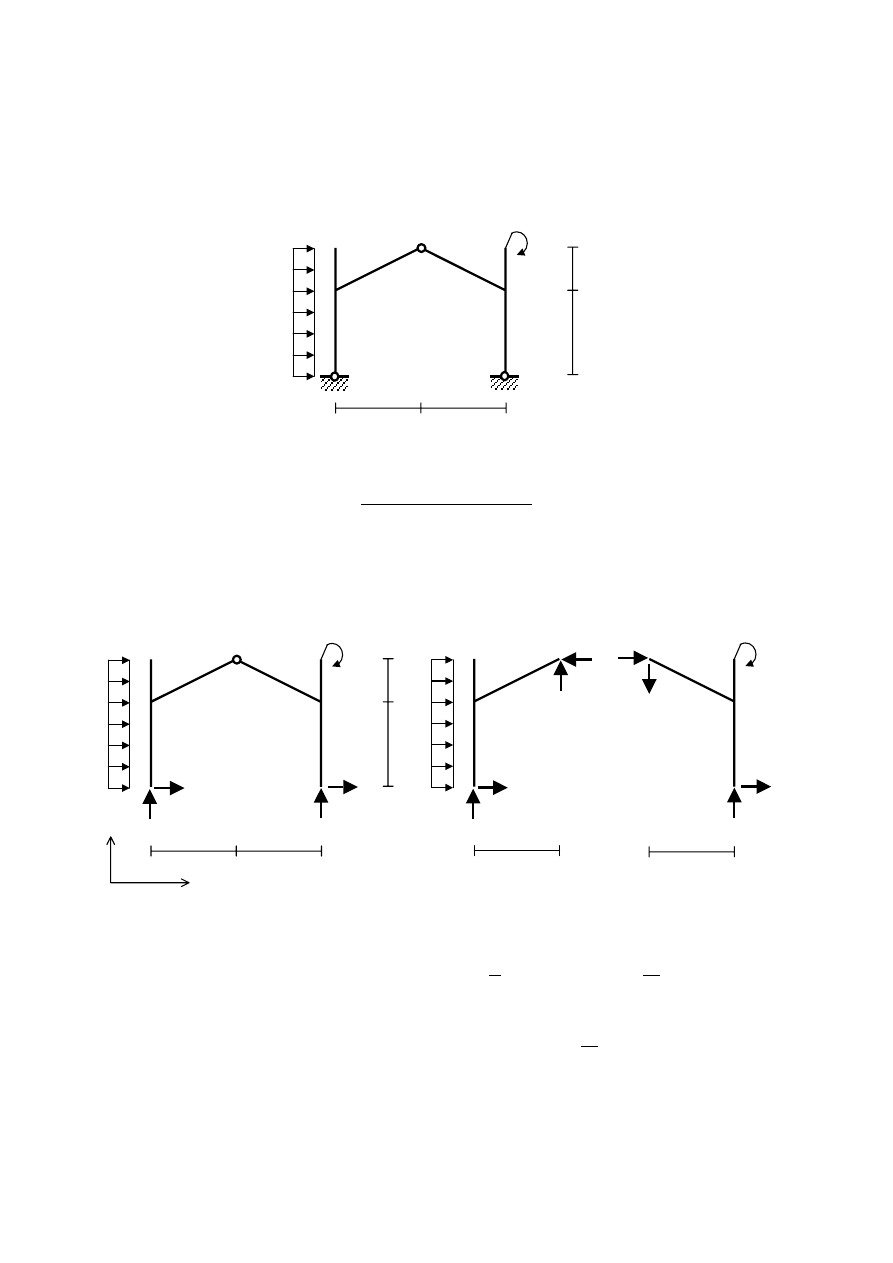
Przykład 3.1. Wyznaczenie zmiany odległości między punktami ramy
trójprzegubowej
Polecenie: Korzystając ze wzoru Maxwella-Mohra wyznaczyć zmianę odległości między
punktami A i B w poniższym układzie. Przyjąć dla wszystkich prętów EI = const.
q
A
B
l
2 l
2 l
2 l
2
ql
W celu wyznaczenia przemieszczenia z wykorzystaniem wzoru Maxwella-Mohra
należy wykonać wykresy momentów gnących od obciążenia rzeczywistego i jednostkowego.
Obciążenie rzeczywiste
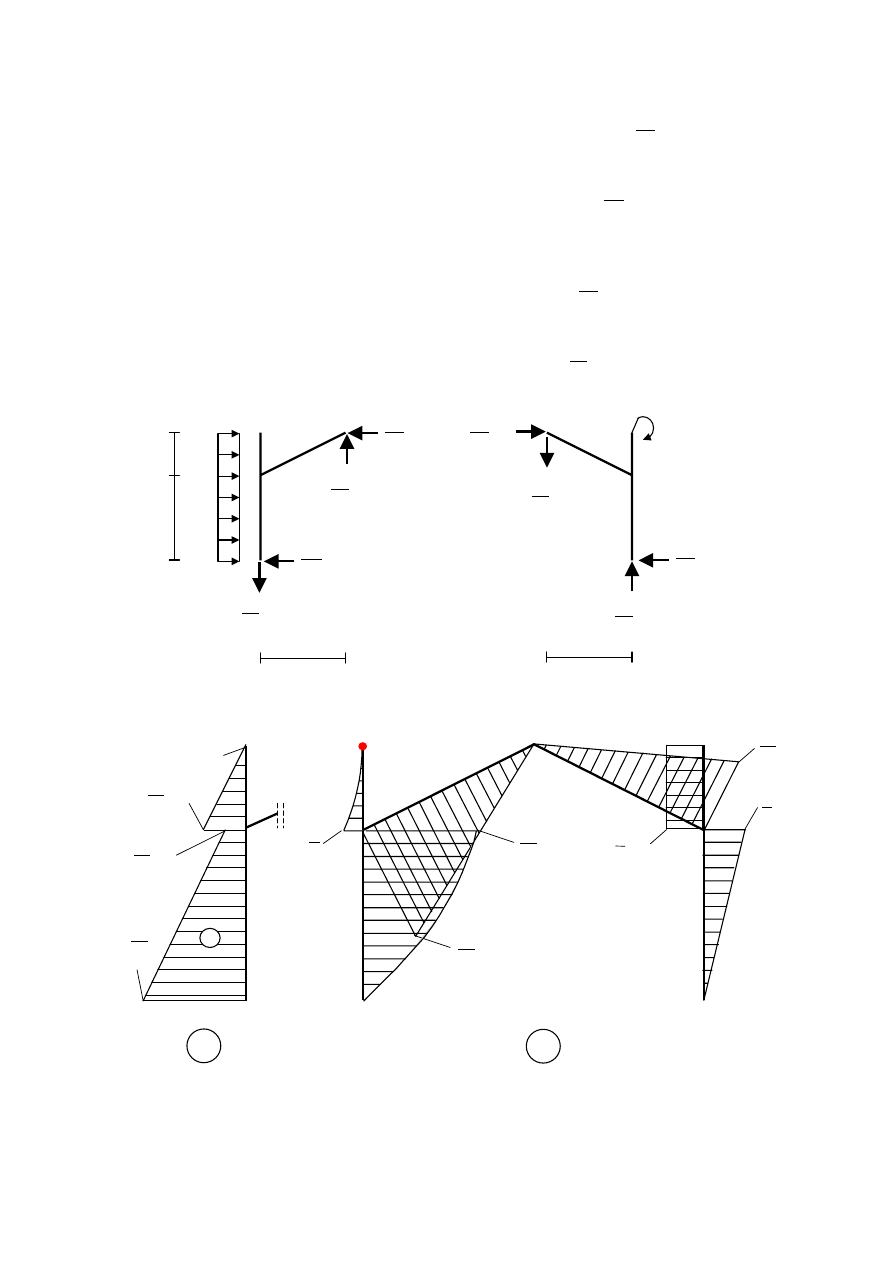
Przed przystąpieniem do sporządzenia wykresu momentów wyznaczymy reakcje
podporowe oraz oddziaływania w przegubie. Oswobodzimy układ od więzów, zastępując
podpory reakcjami. Obie podpory są podporami przegubowymi nieprzesuwnymi. Oznaczmy
lewą podporę literą C, a prawą literą D. Zarówno w punkcie C jak i D działają po dwie
niezależne od siebie składowe reakcji: pionowa i pozioma.
q
A
B
l
2 l
2 l
2 l
D
C
V
C
V
D
H
C
H
D
G
J
F
q
A
2 l
C
V
C
H
C
G
F
H
F
V
F
D
B
V
D
H
D
J
F
H
F
V
F
2 l
y
x
2
ql
2
ql
Z równania sumy momentów względem punktu C dla całego układu wyznaczymy
składową V
D
.
0
=
∑
i
iC
M
:
ql
V
l
l
q
ql
l
V
D
D
⋅
=
⇒
=
⋅
⋅
⋅
−
−
⋅
8
11
0
3
2
1
3
4
2
Z równania sumy rzutów sił na oś pionową dla całego układu obliczymy składową V
C
.
∑
=
i
iy
P
0 :
ql
V
V
V
C
D
C
⋅
−
=
⇒
=
+
8
11
0
Składową poziomą reakcji H
D
wyznaczymy z równania sumy momentów względem
punktu F dla prawego podukładu.
∑
=
i
p
iF
M
0 :
ql
H
ql
l
H
l
V
D
D
D
⋅
−
=
⇒
=
−
⋅
+
⋅
12
7
0
3
2
2
Z równania sumy rzutów sił na oś poziomą dla całego układu obliczymy składową H
C
.
∑
=
i
ix
P
0 :
ql
H
ql
H
H
C
D
C
⋅
−
=
⇒
=
+
+
12
29
0
3
Wyznaczymy teraz oddziaływania w przegubie F, zapisując równania równowagi dla
prawego podukładu. Równanie sumy rzutów sił na oś poziomą ma postać:
∑
=
i
p
ix
P
0 :
ql
H
H
H
F
D
F
⋅
=
⇒
=
+
12
7
0
,
natomiast równanie sumy rzutów sił na oś pionową jest następujące:
∑
=
i
p
iy
P
0 :
ql
V
V
V
F
F
D
⋅
=
⇒
=
−
8
11
0
.
Wykres momentów gnących od obciążenia rzeczywistego jest następujący:
D
B
2
ql
J
F
2 l
ql
⋅
12
7
ql
⋅
8
11
ql
⋅
8
11
ql
⋅
12
7
2 l
l
2 l
q
A
C
G
F
ql
⋅
12
29
ql
⋅
8
11
ql
⋅
8
11
ql
⋅
12
7
1
6
6 =
A
G
C
2
o
2
o
J
G
F
D
C
A
B
1
12
12 =
0
12
5 ≠
12
29
2
1
6
17
3
10
6
13
6
7
0
=
T
+
T
M
mnożnik ql
2
mnożnik ql
2
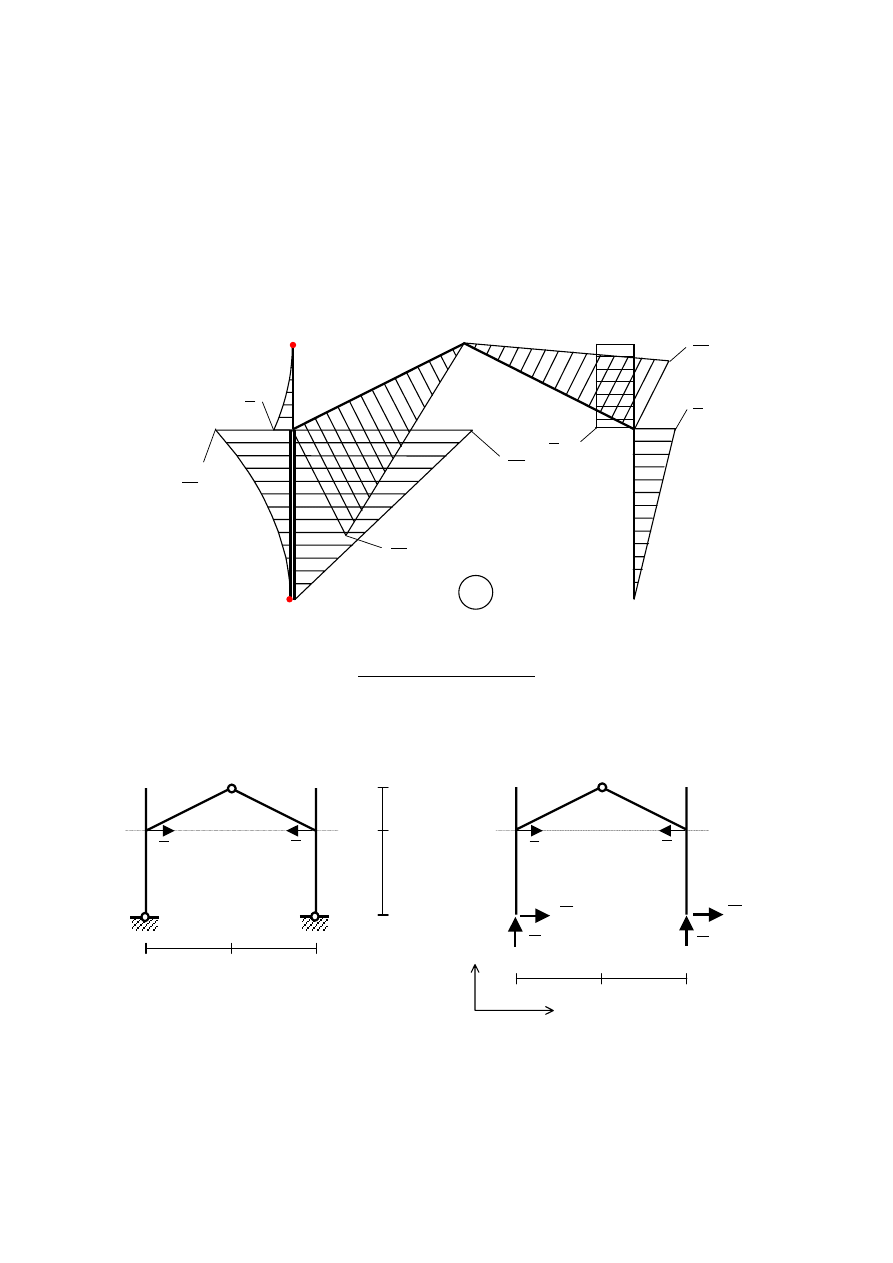
Na lewy słup ramy działa obciążenie ciągłe. Wykonano wykres sił poprzecznych na
tym fragmencie układu. W części dolnej słupa (C
÷A) w żadnym przekroju nie zeruje się siła
poprzeczna, a więc w tym przedziale nie występuje ekstremum na wykresie momentów.
Przed przystąpieniem do wyznaczenia przemieszczenia za pomocą sposobu Wereszczagina,
należy wykres momentów w przedziale (C
÷A) przedstawić jako sumę takich wykresów, dla
których znane jest pole wykresu oraz położenie środka ciężkości (wykres liniowy pochodzi
od składowej poziomej reakcji na podporze C, natomiast wykres paraboliczny od obciążenia
ciągłego). Miejsce zerowe pochodnej funkcji kwadratowej, opisującej moment zginający
wywołany obciążeniem ciągłym, jest oznaczone na wykresie kolorem czerwonym.
Obciążenie jednostkowe
Rozpatrywany układ należy obciążyć obciążeniem jednostkowym, stosownym do
poszukiwanego przemieszczenia. W przypadku wyznaczania zmiany odległości między
punktami A i B należy do tych punktów przyłożyć dwie siły jednostkowe, o kierunku prostej
AB i mające przeciwne zwroty.
A
B
l
2 l
2 l
2 l
1
1
1
6
6 =
M
mnożnik ql
2
6
29
2
1
3
10
6
13
2
6
12
=
6
7
x
A
B
2 l
2 l
F
J
G
D
C
1
1
C
V
C
H
D
V
D
H
y
2
o
2
o
W celu sporządzenia wykresów momentów wyznaczymy reakcje podporowe oraz
oddziaływania w przegubie. Oswobodzimy układ od więzów, zastępując podpory reakcjami.
Obie podpory są podporami przegubowymi nieprzesuwnymi. Zarówno w punkcie C jak i D
działają po dwie niezależne od siebie składowe reakcji: pionowa i pozioma.
3
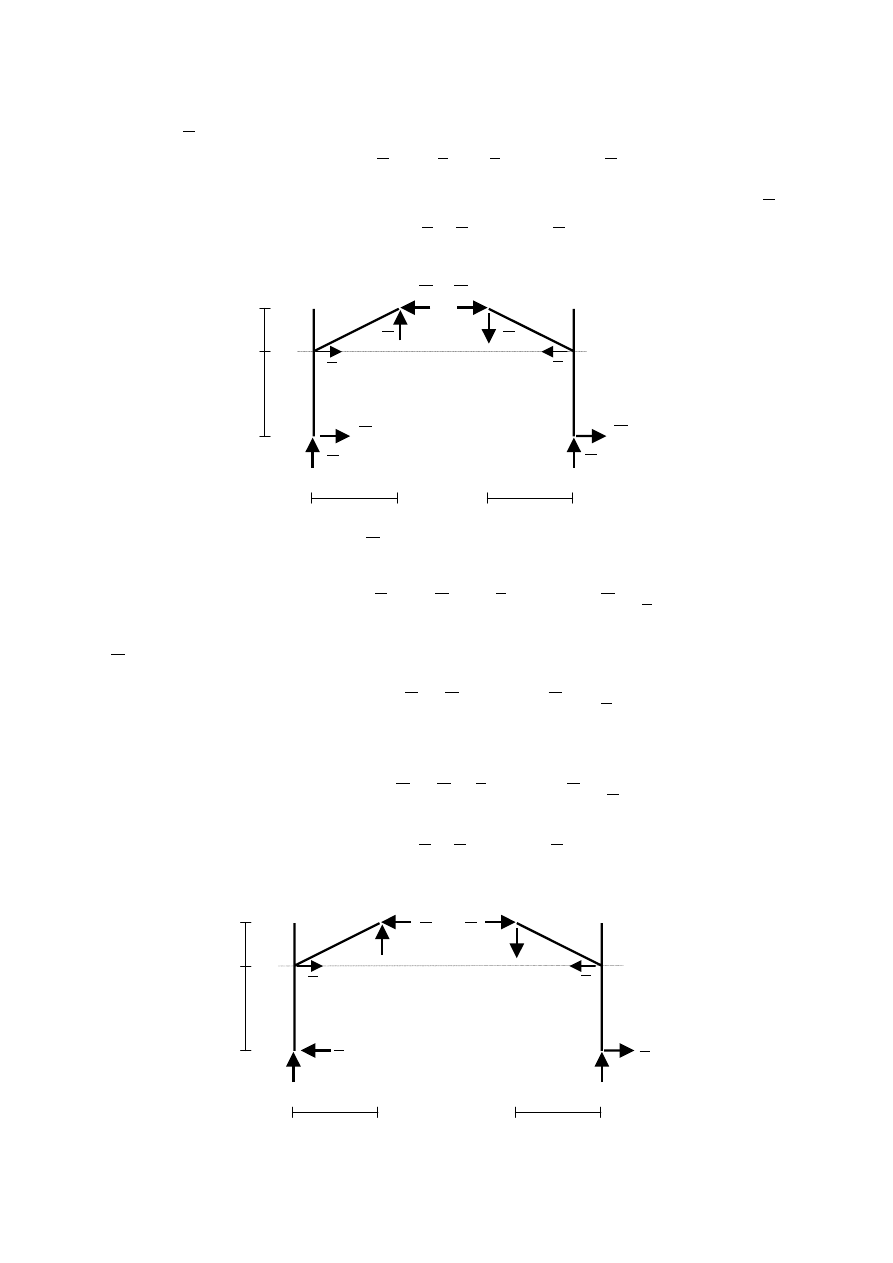
Z równania sumy momentów względem punktu C dla całego układu wyznaczymy
składową
D
V .
0
=
∑
i
iC
M
:
0
0
2
1
2
1
4
=
⇒
=
⋅
−
⋅
+
⋅
D
D
V
l
l
l
V
Z równania sumy rzutów sił na oś pionową dla całego układu obliczymy składową
C
V .
∑
=
i
iy
P
0 :
0
0
=
⇒
=
+
C
D
C
V
V
V
F
H
F
A
2 l
C
G
F
D
B
J
2 l
l
2 l
F
V
C
V
C
H
D
V
D
H
F
V
F
H
1
1
Składową poziomą reakcji
D
H wyznaczymy z równania sumy momentów względem
punktu F dla prawego podukładu.
∑
=
i
p
iF
M
0 :
3
1
0
1
3
2
=
⇒
=
⋅
−
⋅
+
⋅
D
D
D
H
l
l
H
l
V
Z równania sumy rzutów sił na oś poziomą dla całego układu obliczymy składową
C
H .
∑
=
i
ix
P
0 :
3
1
0
−
=
⇒
=
+
C
D
C
H
H
H
Wyznaczymy teraz oddziaływania w przegubie F, zapisując równania równowagi dla
prawego podukładu. Równanie sumy rzutów sił na oś poziomą ma postać:
∑
=
i
p
ix
P
0 :
3
2
0
1
=
⇒
=
−
+
F
D
F
H
H
H
,
natomiast równanie sumy rzutów sił na oś pionową jest następujące:
∑
=
i
p
iy
P
0 :
0
0
=
⇒
=
−
F
F
D
V
V
V
.
3
1
F
A
C
G
F
D
B
J
l
2 l
3
1
1
1
0
0
3
2
3
2
0
0
2 l
2 l
4
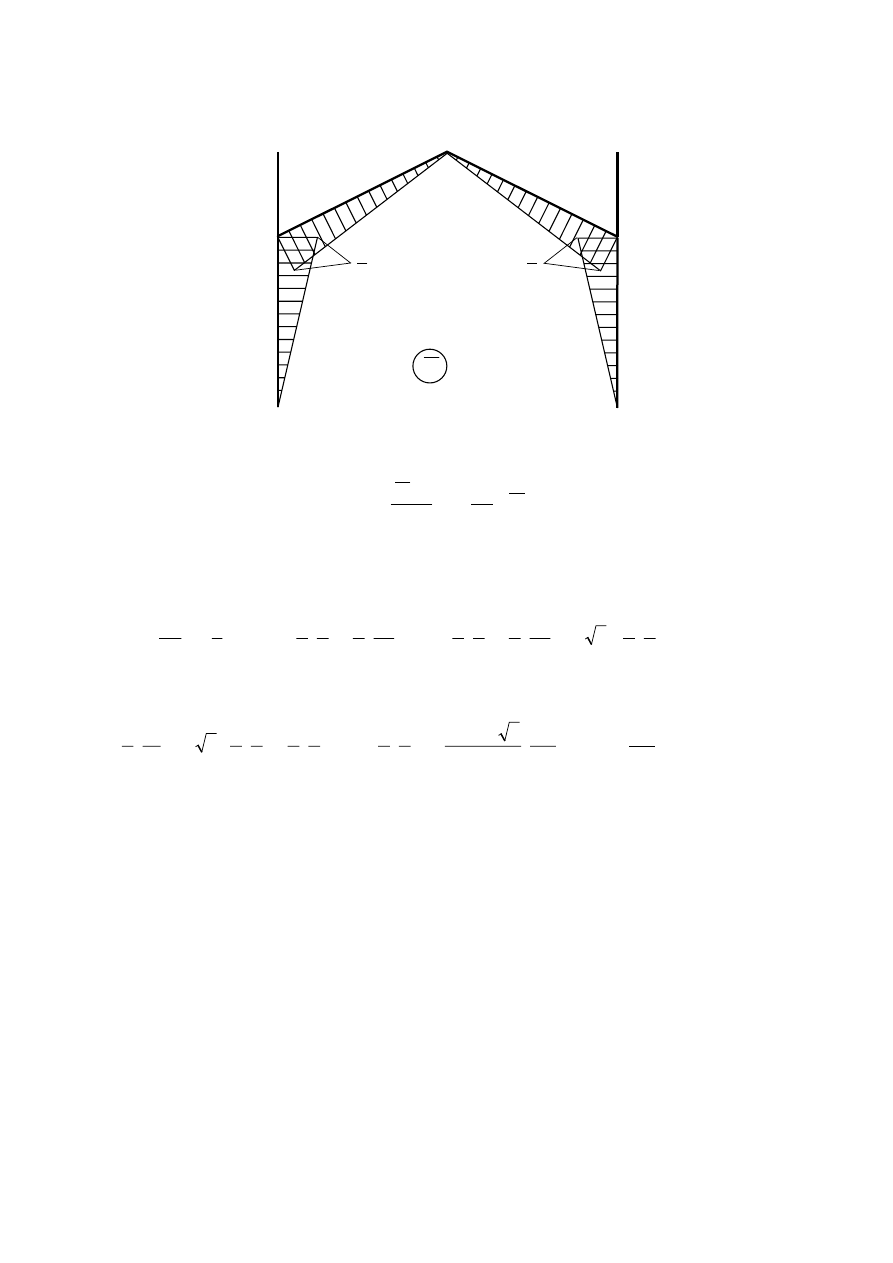
Wykres momentów gnących od obciążenia jednostkowego jest następujący:
J
M
mnożnik l
3
2
3
2
F
G
B
A
D
C
Korzystając ze wzoru Maxwella-Mohra wyznaczymy zmianę odległości między
punktami A i B.
ds
M
M
EI
ds
EI
M
M
l
s
s
AB
∫
∫
=
=
∆
1
Całkowanie możemy wykonać sposobem Wereszczagina, ponieważ w każdym
przedziale całkowania co najmniej jedna z funkcji podcałkowych jest liniowa.
+
⎜
⎜
⎜
⎝
⎛
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
−
⋅
=
∆
4
4
4
3
4
4
4
2
1
4
4
4
4
4
4
4
3
4
4
4
4
4
4
4
2
1
AF
CA
AB
l
l
ql
l
l
ql
l
l
ql
EI
l
3
2
3
2
5
6
20
2
1
3
2
3
2
2
6
29
2
1
3
2
4
3
2
2
3
1
1
2
2
2
EI
ql
EI
ql
l
l
ql
l
l
ql
BD
FB
4
4
2
2
5427
,
1
27
5
7
26
3
2
3
2
2
6
7
2
1
3
2
3
2
5
6
13
2
1
⋅
≅
⋅
⋅
+
=
⎟
⎟
⎟
⎠
⎞
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
−
4
4
4
3
4
4
4
2
1
4
4
4
4
3
4
4
4
4
2
1
Znak dodatni obliczonego przemieszczenia świadczy o tym, że punkty A i B zbliżą się
do siebie, ponieważ zwrot przemieszczenia jest zgodny ze zwrotem obciążenia
jednostkowego.
5
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron