
Wydawnictwo Helion
ul. Chopina 6
44-100 Gliwice
tel. (32)230-98-63
IDZ DO
IDZ DO
KATALOG KSI¥¯EK
KATALOG KSI¥¯EK
TWÓJ KOSZYK
TWÓJ KOSZYK
CENNIK I INFORMACJE
CENNIK I INFORMACJE
CZYTELNIA
CZYTELNIA
Teoria sygna³ów. Wstêp.
Wydanie II poprawione
i uzupe³nione
Autorzy: Jacek Izydorczyk, Grzegorz P³onka, Grzegorz Tyma
ISBN: 83-246-0401-4
Format: B5, stron: 304
Kompendium wiedzy na temat sygna³ów i metod ich przetwarzania
• Modulacja sygna³ów
• Transformaty Fouriera i Laplace’a
• Filtry analogowe i cyfrowe
Teoria sygna³ów to jedna z fundamentalnych dziedzin wiedzy technicznej.
Jej znajomoœæ jest niezbêdna nie tylko projektantom urz¹dzeñ elektronicznych,
ale równie¿ automatykom, informatykom, elektrotechnikom i specjalistom od
telekomunikacji. Rozwój techniki cyfrowej zrewolucjonizowa³ metody przetwarzania
sygna³ów, lecz podstawy tych mechanizmów s¹ niezmienne — nadal wykorzystywane
s¹ transformaty Fouriera i Laplace’a, klasyczne algorytmy modulacji oraz regu³y
projektowania urz¹dzeñ.
Ksi¹¿ka „Teoria sygna³ów. Wstêp. Wydanie II” to kolejne wydanie publikacji
poœwiêconej sygna³om i ich przetwarzaniu. Zawiera zbiór najwa¿niejszych informacji
zwi¹zanych z przekszta³caniem i modulowaniem sygna³ów metodami analogowymi
i cyfrowymi oraz projektowaniem filtrów aktywnych i pasywnych. Ka¿dy jej rozdzia³
stanowi osobny wyk³ad uzupe³niony przyk³adami i zadaniami do samodzielnego
rozwi¹zania, który mo¿na przeczytaæ bez odwo³ywania siê do pozosta³ych wyk³adów.
• Szeregi i transformaty Fouriera
• Modulacja sygna³ów
• Przekszta³cenie Laplace’a
• Projektowanie filtrów analogowych
• Sygna³y dyskretne i cyfrowe
• Modulacja impulsowa
• Dyskretna transformata Fouriera
• Liniowe uk³ady cyfrowe
• Projektowanie filtrów cyfrowych
Opanuj podstawy technologii cyfrowej

Spis treści
Rozdział 1. Szereg Fouriera . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
1.1.
Wst ˛
ep . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
1.2.
Definicja rozwini ˛
ecia w szereg Fouriera . . . . . . . . . . . . . . . . . . . . . . . . . .
10
1.3.
Warunki Dirichleta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
1.4.
Wybrane własno´sci szeregów Fouriera . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
1.5.
Stan ustalony w obwodach liniowych z wymuszeniami okresowymi . . . . . . . . .
20
1.6.
Przykłady zastosowa ´
n szeregów Fouriera . . . . . . . . . . . . . . . . . . . . . . . . .
22
1.7.
Literatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
26
1.8.
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
26
Rozdział 2. Transformacja Fouriera . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
2.1.
Definicja przekształcenia Fouriera . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
2.2.
Warunki Dirichleta istnienia transformaty Fouriera . . . . . . . . . . . . . . . . . . .
33
2.3.
Wybrane własno´sci przekształcenia Fouriera . . . . . . . . . . . . . . . . . . . . . . .
34
2.4.
G ˛
esto´s´c widmowa sygnału na wyj´sciu układu liniowego . . . . . . . . . . . . . . . .
39
2.5.
Przykłady . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
39
2.6.
Literatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
48
Rozdział 3. Modulacja . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
3.1.
Wst ˛
ep . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
3.2.
Modulacja w pa´smie podstawowym . . . . . . . . . . . . . . . . . . . . . . . . . . . .
50
3.3.
Modulacja sygnału sinusoidalnego . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
51
3.3.1.
Modulacja amplitudowa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
51
3.3.2.
Przemiana cz ˛
estotliwo´sci
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
58
3.3.3.
Modulacja k ˛
atowa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
60
3.3.4.
Modulacja kwadraturowa
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
64
3.4.
Literatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
3.5.
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
66

6
Spis treści
Rozdział 4. Przekształcenie Laplace’a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67
4.1.
Przekształcenie Laplace’a
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67
4.2.
Odwrotna transformacja Laplace’a . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
73
4.2.1.
Wzór Riemanna-Mellina . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
73
4.2.2.
Funkcje wymierne, residua i rozkład na ułamki proste . . . . . . . . . . . .
77
4.3.
Własno´sci przekształcenia Laplace’a . . . . . . . . . . . . . . . . . . . . . . . . . . . .
81
4.3.1.
Liniowo´s´c transformaty
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
81
4.3.2.
Transformata pochodnej sygnału
L -transformowalnego . . . . . . . . . .
81
4.3.3.
Transformata całki sygnału
L -transformowalnego . . . . . . . . . . . . . .
82
4.3.4.
Granica sygnału w zerze . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
82
4.3.5.
Pochodna transformaty sygnału
L -transformowalnego . . . . . . . . . . .
82
4.3.6.
Opó´znienie sygnału
L -transformowalnego . . . . . . . . . . . . . . . . . .
83
4.3.7.
Przesuni ˛
ecie argumentu obrazu
L -transformowalnego . . . . . . . . . . .
83
4.3.8.
Transformata sygnału okresowego . . . . . . . . . . . . . . . . . . . . . . . .
83
4.3.9.
Transformata splotu sygnałów
L -transformowalnych . . . . . . . . . . . .
84
4.4.
Zastosowanie przekształcenia Laplace’a
. . . . . . . . . . . . . . . . . . . . . . . . .
84
4.4.1.
Równania ró˙zniczkowe zwyczajne
. . . . . . . . . . . . . . . . . . . . . . . .
84
4.4.2.
Równania ró˙zniczkowe cz ˛
astkowe
. . . . . . . . . . . . . . . . . . . . . . . .
88
4.4.3.
Równania całkowe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
90
4.5.
Transmitancja . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
91
4.5.1.
Odpowied´z impulsowa układu
. . . . . . . . . . . . . . . . . . . . . . . . . .
94
4.5.2.
Badanie stabilno´sci układu
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
95
4.5.3.
Transmitancja operatorowa a transmitancja symboliczna . . . . . . . . . . 100
4.6.
Literatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
4.7.
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
Rozdział 5. Filtry analogowe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
5.1.
Filtr idealny . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
5.2.
Aproksymacja charakterystyki amplitudowej filtru idealnego . . . . . . . . . . . . . 108
5.2.1.
Filtr Butterwortha . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
5.2.2.
Aproksymacja Czebyszewa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
5.2.3.
Przekształcenia cz ˛
estotliwo´sci . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
5.3.
Synteza pasywnych filtrów LC o charakterystyce Butterwortha i Czebyszewa . . . . 132
5.3.1.
Obwód ła ´
ncuchowy otwarty na ko ´
ncu . . . . . . . . . . . . . . . . . . . . . . 133
5.3.2.
Obci ˛
a˙zony obwód ła ´
ncuchowy . . . . . . . . . . . . . . . . . . . . . . . . . . 141
5.3.3.
Wzory dla syntezy filtrów Butterwortha — symetryczny obwód ła ´
ncuchowy 143
5.3.4.
Wzory dla syntezy filtrów Butterwortha . . . . . . . . . . . . . . . . . . . . . 144
5.3.5.
Wzory dla syntezy filtrów Czebyszewa . . . . . . . . . . . . . . . . . . . . . . 146
5.3.6.
Przekształcenia cz ˛
estotliwo´sci raz jeszcze . . . . . . . . . . . . . . . . . . . . 148
5.3.7.
Kilka słów o projektowaniu filtrów pasywnych . . . . . . . . . . . . . . . . . 152
5.4.
Synteza filtrów aktywnych RC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 153
5.4.1.
Idealny wzmacniacz operacyjny . . . . . . . . . . . . . . . . . . . . . . . . . . 153
5.4.2.
Kaskadowy filtr aktywny . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157
5.4.3.
Równoległy filtr aktywny . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157
5.4.4.
Transmitancje rz ˛
edu drugiego . . . . . . . . . . . . . . . . . . . . . . . . . . . 158
5.4.5.
Układy z wielokrotnym sprz ˛
e˙zeniem zwrotnym . . . . . . . . . . . . . . . . 160
5.5.
Charakterystyka opó´znienia grupowego . . . . . . . . . . . . . . . . . . . . . . . . . . 164
5.5.1.
Opó´znienie grupowe filtru o stałych skupionych . . . . . . . . . . . . . . . . 164

Spis treści
7
5.5.2.
Wyrównywanie charakterystyki fazowej filtru . . . . . . . . . . . . . . . . . . 166
5.5.3.
Meandry przyczynowo´sci . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 169
5.6.
Literatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172
5.7.
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 173
Rozdział 6. Modulacja impulsowa, sygnały dyskretne i cyfrowe . . . . . . . . . . . . . . . . 175
6.1.
Transformata Fouriera dystrybucji delta Diraca . . . . . . . . . . . . . . . . . . . . . 175
6.1.1.
Transformaty Fouriera funkcji trygonometrycznych . . . . . . . . . . . . . . 175
6.1.2.
Transformata Fouriera skoku jednostkowego . . . . . . . . . . . . . . . . . . 176
6.1.3.
Transformata Fouriera całki sygnału . . . . . . . . . . . . . . . . . . . . . . . 178
6.1.4.
Transformata Fouriera szeregu impulsów Diraca . . . . . . . . . . . . . . . . 179
6.1.5.
Transformata Fouriera funkcji okresowej . . . . . . . . . . . . . . . . . . . . 181
6.1.6.
Reguła sumacyjna Poissona . . . . . . . . . . . . . . . . . . . . . . . . . . . . 182
6.2.
Sygnał o ograniczonym pa´smie cz ˛
estotliwo´sci i sygnał o ograniczonym czasie
trwania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 183
6.2.1.
Nierówno´s´c Schwartza . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 183
6.2.2.
Własno´sci sygnałów o ograniczonym czasie trwania
. . . . . . . . . . . . . 184
6.2.3.
Własno´sci sygnałów o ograniczonym pa´smie cz ˛
estotliwo´sci . . . . . . . . . 185
6.3.
Sygnał dyskretny . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 189
6.3.1.
Modulacja impulsowa — sygnał dyskretny . . . . . . . . . . . . . . . . . . . 189
6.3.2.
Widmo sygnału dyskretnego . . . . . . . . . . . . . . . . . . . . . . . . . . . . 190
6.3.3.
Odtwarzanie sygnału analogowego na podstawie sygnału dyskretnego . . 191
6.3.4.
Twierdzenie Kotelnikowa-Shannona-Nyquista . . . . . . . . . . . . . . . . . 194
6.3.5.
Wpływ kształtu sygnałów próbkuj ˛
acych na widmo sygnału zmodulowanego 195
6.3.6.
Decymacja i interpolacja . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 196
6.3.7.
Dowód twierdzenia o próbkowaniu bez teorii dystrybucji . . . . . . . . . . 198
6.3.8.
Próbkowanie sygnałów pasmowych — obwiednia sygnału . . . . . . . . . . 200
6.4.
Sygnał cyfrowy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206
6.4.1.
Stałoprzecinkowy, binarny format zapisu liczb . . . . . . . . . . . . . . . . . 206
6.4.2.
Zmiennoprzecinkowy, binarny format zapisu liczb . . . . . . . . . . . . . . 207
6.4.3.
Podział kanału w dziedzinie czasu (TDM — time division multiplexing) . 209
6.4.4.
Szumy kwantowania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 210
6.4.5.
Przetwarzanie
∆Σ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 211
6.4.6.
Wzór Shannona
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 223
6.5.
Literatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 224
6.6.
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 225
Rozdział 7. Dyskretna transformacja Fouriera . . . . . . . . . . . . . . . . . . . . . . . . . . 227
7.1.
Dyskretna transformacja Fouriera . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 227
7.1.1.
Sygnał dyskretny o sko ´
nczonym czasie trwania i jego widmo . . . . . . . . 227
7.1.2.
Dyskretna transformacja Fouriera . . . . . . . . . . . . . . . . . . . . . . . . . 229
7.1.3.
Własno´sci DFT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231
7.2.
Szybki algorytm obliczania dyskretnej transformaty Fouriera (FFT) . . . . . . . . . 240
7.2.1.
Algorytm FFT z podziałem w dziedzinie czasu . . . . . . . . . . . . . . . . . 240
7.2.2.
Algorytm FFT z podziałem w dziedzinie cz ˛
estotliwo´sci . . . . . . . . . . . . 242
7.2.3.
O dodawaniu i mno˙zeniu liczb przez komputery
. . . . . . . . . . . . . . . 244
7.2.4.
Przykłady zastosowa ´
n DFT poza cyfrowym przetwarzaniem sygnałów . . . 249
7.3.
Algorytm ´swiergotowy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 252

7.4.
Literatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 255
7.5.
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 255
Rozdział 8. Transformacja
Z . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 257
8.1.
Wst ˛
ep . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 257
8.2.
Definicja transformacji
Z . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 257
8.3.
Transformacja odwrotna . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 260
8.4.
Transformacja
Z sygnału przyczynowego . . . . . . . . . . . . . . . . . . . . . . . . 261
8.5.
Transformacja sygnału stabilnego . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 262
8.6.
Własno´sci transformacji
Z . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 263
8.7.
Zwi ˛
azek z transformacj ˛
a Fouriera
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 267
8.8.
Literatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 268
8.9.
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 268
Rozdział 9. Liniowe układy dyskretne . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 269
9.1.
Wst ˛
ep . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 269
9.2.
Równania ró˙znicowe i równania stanu
. . . . . . . . . . . . . . . . . . . . . . . . . . 269
9.3.
Odpowied´z impulsowa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 272
9.4.
Transmitancja . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 273
9.5.
Przyczynowo´s´c i stabilno´s´c układów cyfrowych a obszar zbie˙zno´sci transmitancji
276
9.6.
Charakterystyka cz ˛
estotliwo´sciowa a zera i bieguny transmitancji . . . . . . . . . . 276
9.7.
Literatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 277
9.8.
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 278
Rozdział 10. Filtry cyfrowe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 279
10.1. Filtry SOI . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 280
10.1.1. Metoda okien czasowych . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 281
10.2. Filtry NOI . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 285
10.2.1. Projektowanie filtrów NOI . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 285
10.3. Literatura . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 292
Skorowidz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 293

Transformacja Fouriera
Grzegorz Tyma
2
2.1. Definicja przekształcenia Fouriera
Spróbujmy znale´z´c wzory na transformacj ˛
e Fouriera sygnałów aperiodycznych, korzy-
staj ˛
ac z wyników otrzymanych dla szeregów Fouriera. Pomysł jest nast ˛
epuj ˛
acy: niech
analizowany sygnał aperiodyczny zostanie na chwil ˛
e zamieniony na okresowy przez
jego powielenie z okresem T . Dla takiego sygnału potrafimy znale´z´c rozwini ˛
ecie. Na-
st ˛
epnie sprawdzimy, jak b ˛
ed ˛
a si ˛
e zachowywały współczynniki rozwini ˛
ecia w przypad-
ku, gdy z okresem b ˛
edziemy zd ˛
a˙za´c do niesko ´
nczono´sci. Zabieg ten spowoduje, i˙z nasz
sztucznie powielony, okresowy przebieg znów zamieni si ˛
e w sygnał aperiodyczny.
Rozpatrzmy przypadek sygnału okresowego, którego rozwini ˛
ecie zostało znalezione
w przykładzie 1.8, w rozdziale po´swi ˛
econym szeregom Fouriera. Sygnał ten, o okre-
sie T , mo˙ze by´c opisany wzorem
x(t ) =
(
1 ,
gdy
|t |< T
1
,
0 ,
gdy
T
1
< |t |< T /2 .
(2.1)
Znalezione współczynniki rozwini ˛
ecia maj ˛
a posta´c
c
k
=
2 sin(k
ω
0
T
1
)
k
ω
0
T
,
gdzie
ω
0
=
2
π
T
.
(2.2)
Zdefiniujmy now ˛
a wielko´s´c w postaci
T c
k
=
2 sin(
ωT
1
)
ω
¯
¯
¯
¯
ω=kω
0
(2.3)
i nazwijmy funkcj ˛
e stoj ˛
ac ˛
a po prawej stronie równo´sci obwiedni ˛
a. Współczynniki roz-
wini ˛
ecia mog ˛
a by´c traktowane jako próbki obwiedni pobierane w równych odst ˛
epach
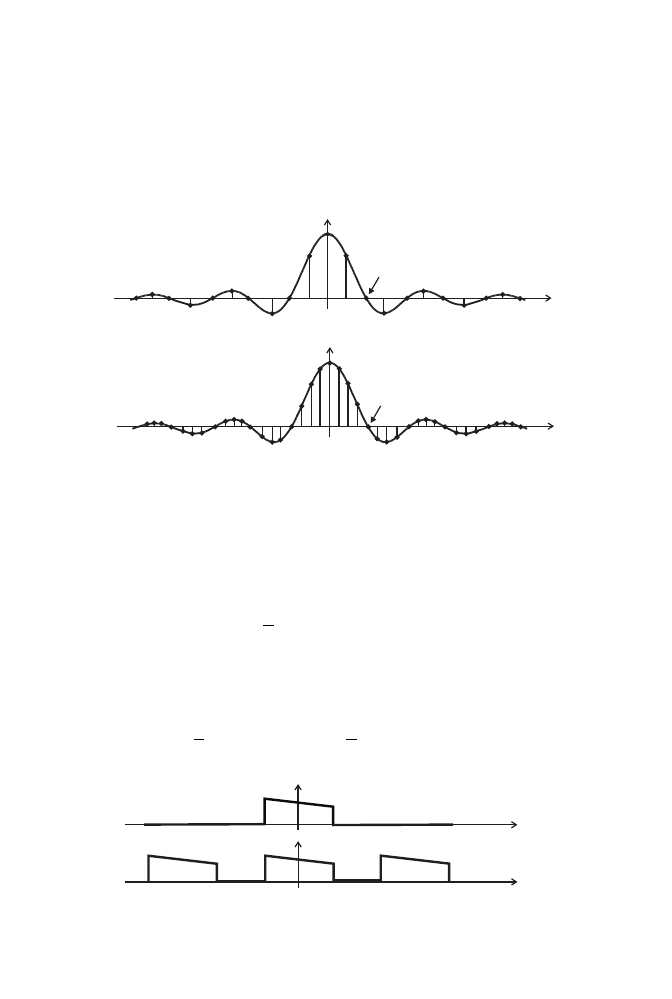
32
2. Transformacja Fouriera
(rysunek 2.1). Dla ustalonej warto´sci T
1
obwiednia jest niezale˙zna od T . Wraz ze wzro-
stem T malej ˛
a odst ˛
epy pomi ˛
edzy pobieranymi próbkami obwiedni. W granicznym
przypadku, gdy T d ˛
a˙zy do niesko ´
nczono´sci, sygnał okresowy staje si ˛
e sygnałem ape-
riodycznym, a próbki T c
k
tworz ˛
a obwiedni ˛
e.
w
k
Tc
w
k
Tc
1
4
T
T
=
×
a)
1
4
T
T
=
×
a)
1
8
T
T
=
×
b)
0
2 w
×
0
4 w
×
Rysunek 2.1.
Obwiednia
T c
k
i próbki pobierane z niej z okresem próbkowania
(a)
T = 4T
1
i
(b)
T = 8T
1
Oznaczmy sztucznie utworzony sygnał okresowy przez x
1
(t ) (rysunek 2.2). Mo˙zemy
dla niego napisa´c znane wzory rozwini ˛
ecia w szereg Fouriera:
x
1
(t ) =
∞
X
k=−∞
c
k
e
jk
ω
0
t
,
(2.4a)
c
k
=
1
T
Z
T /2
−T /2
x
1
(t ) e
−jkω
0
t
dt ,
(2.4b)
gdzie
ω
0
= 2π/T . Sygnał okresowy x
1
(t ) powstał przez powielenie z okresem T sygnału
x(t ), zatem x
1
(t ) = x(t ) dla |t| < T /2, ponadto x(t ) = 0 poza tym przedziałem. Korzysta-
j ˛
ac z tych informacji mo˙zemy poprzedni wzór zapisa´c w postaci
c
k
=
1
T
Z
T /2
−T /2
x(t ) e
−jkω
0
t
dt =
1
T
Z
∞
−∞
x(t ) e
−jkω
0
t
dt .
(2.5)
( )
x t
1
( )
x t
t
t
1
T
1
T
1
T
-
1
T
-
T
T
-
Rysunek 2.2.
Sygnał aperiodyczny
x(t ) i sztucznie utworzony sygnał okresowy x
1
(
t )

2.2. Warunki Dirichleta istnienia transformaty Fouriera
33
Zatem obwiedni ˛
e X (j
ω) z T c
k
mo˙zna przedstawi´c jako
X (j
ω) =
Z
∞
−∞
x(t ) e
−jωt
dt .
(2.6)
Współczynniki rozwini ˛
ecia wyliczamy:
c
k
=
1
T
X (jk
ω
0
) .
(2.7)
Korzystaj ˛
ac z tego, otrzymujemy
x
1
(t ) =
∞
X
k=−∞
1
T
X (jk
ω
0
) e
jk
ω
0
t
=
1
2
π
∞
X
k=−∞
X (jk
ω
0
) e
jk
ω
0
t
ω
0
.
(2.8)
Gdy okres T d ˛
a˙zy do niesko ´
nczono´sci, to x
1
(t ) d ˛
a˙zy do x(t ), a
ω
0
d ˛
a˙zy do zera. W efek-
cie w ostatnim wzorze x(t ) zast ˛
api x
1
(t ), a po prawej stronie suma zostanie zast ˛
apiona
całk ˛
a
x(t ) =
1
2
π
Z
∞
−∞
X (j
ω)e
j
ωt
d
ω.
(2.9)
Ostatecznie otrzymali´smy par ˛
e wzorów na proste i odwrotne przekształcenie Fouriera:
X (j
ω) =
Z
∞
−∞
x(t ) e
−jωt
dt ,
(2.10a)
x(t ) =
1
2
π
Z
∞
−∞
X (j
ω)e
j
ωt
d
ω.
(2.10b)
Funkcja po transformacji mo˙ze by´c zapisana we współrz ˛
ednych biegunowych:
X (j
ω) = |X (jω)|e
j arg
[
X (j
ω)
] .
(2.11)
Moduł X (
ω) = |X (jω)| nosi nazw˛e g˛esto´sci widmowej amplitudy, natomiast faza ϕ(ω) =
arg
£X (j
ω)¤ nazywana jest g˛esto´sci ˛a widmow ˛a fazy (cz˛esto zamiennie mówi si˛e o wid-
mie amplitudowym i fazowym).
Podane zostan ˛
a teraz warunki, jakie musi spełnia´c funkcja x(t ), aby mo˙zna było
znale´z´c jej transformat ˛
e Fouriera.
2.2. Warunki Dirichleta istnienia transformaty Fouriera
Podobnie jak dla sygnałów okresowych podaje si ˛
e trzy warunki, zwane warunkami Di-
richleta, na istnienie transformacji Fouriera funkcji x(t ).
Warunek 1. Funkcja x(t ) jest bezwzgl˛ednie całkowalna, tzn.
Z
∞
−∞
|x(t )| dt < ∞.
(2.12)
Warunek 2. Funkcja x(t ) ma sko ´
nczon ˛
a liczb˛e maksimów i minimów w dowolnym
sko ´
nczonym przedziale.

34
2. Transformacja Fouriera
Warunek 3. Funkcja x(t ) ma sko ´
nczon ˛
a liczb˛e punktów nieci ˛
agło´sci w dowolnym
sko ´
nczonym przedziale. Ponadto warto´sci funkcji w tych punktach musz ˛
a by´c ogra-
niczone.
W kolejnym podrozdziale przedstawiono wybrane własno´sci przekształcenia Fouriera.
2.3. Wybrane własności przekształcenia Fouriera
Liniowość
Je˙zeli
x(t ) ˆ
= X (jω) oraz
y(t ) ˆ
= Y (jω),
(2.13a)
to
a x(t ) + b y(t ) ˆ
= a X (jω) + b Y (jω) .
(2.13b)
Dowód twierdzenia o liniowo´sci przekształcenia Fouriera jest łatwy i wynika wprost ze
wzoru na proste przekształcenie Fouriera.
Przesunięcie w czasie
Je˙zeli x(t ) ˆ
= X (jω), to x(t − t
0
) ˆ
= e
−jωt
0
X (j
ω). Udowodnijmy to. Wiemy, i˙z
x(t ) =
1
2
π
Z
∞
−∞
X (j
ω)e
j
ωt
d
ω.
(2.14)
Wprowadzaj ˛
ac przesuni ˛
ecie w czasie, otrzymujemy
x(t − t
0
) =
1
2
π
Z
∞
−∞
X (j
ω)e
j
ω(t−t
0
)
d
ω =
1
2
π
Z
∞
−∞
e
−jωt
0
X (j
ω)e
j
ωt
d
ω.
(2.15)
Dostajemy zatem
F ©x(t − t
0
)
ª = e
−jωt
0
X (j
ω).
(2.16)
Warto zauwa˙zy´c, ˙ze przesuni ˛
ecie oryginału powoduje zmian ˛
e jedynie g ˛
esto´sci widmo-
wej fazy, natomiast bez zmiany pozostaje g ˛
esto´s´c widmowa amplitudy.
Przesunięcie w dziedzinie częstotliwości
Je˙zeli x(t ) ˆ
= X (jω), to e
j
ω
0
t
x(t ) ˆ
= X [j(ω − ω
0
)]. Udowodnijmy to. Wiemy, i˙z
x(t ) =
1
2
π
Z
∞
−∞
X (j
ω)e
j
ωt
d
ω.
(2.17)
Wprowadzaj ˛
ac przesuni ˛
ecie w cz ˛
estotliwo´sci, otrzymujemy
F
−1
©X [j(
ω − ω
0
)]
ª =
1
2
π
Z
∞
−∞
X [j(
ω − ω
0
)] e
j
ωt
d
ω =
=
e
j
ω
0
t
2
π
Z
∞
−∞
X (v ) e
jv t
dv = e
j
ω
0
t
x(t ) .
(2.18)

2.3. Wybrane własności przekształcenia Fouriera
35
Różniczkowanie i całkowanie oryginału
Zró˙zniczkujmy wzór x(t ) =
1
2
π
R
∞
−∞
X (j
ω)e
j
ωt
d
ω po czasie; w efekcie otrzymamy
dx(t )
dt
ˆ
= jωX (jω)
(2.19)
Twierdzenie powy˙zsze jest prawdziwe, gdy funkcja x(t ) jest bezwzgl ˛
ednie całkowalna
w przedziale (−∞,+∞), ci ˛
agła i d ˛
a˙zy do zera dla t → ±∞ oraz ma prawie wsz ˛edzie
pochodn ˛
a ˙
x(t ), która jest bezwzgl ˛
ednie całkowalna w przedziale (−∞,+∞).
Niestety wzór na transformat ˛
e Fouriera całki nie jest tak prosty, jak w przypadku
transformaty Laplace’a:
Z
t
−∞
x(
ζ)dζ ˆ=
X (j
ω)
j
ω
+ π X (0) δ(ω) .
(2.20)
Aby go udowodni´c, trzeba zauwa˙zy´c, ˙ze sygnał
R
t
−∞
x(
ζ)dζ jest splotem sygnału x(t)
z jedynk ˛
a Heaviside’a
1(t ) =
(
1
dla
t Ê 0 ,
0
dla
t < 0 ,
(2.21)
i zastosowa´c twierdzenie o transformacie Fouriera splotu sygnałów
1
.
Skalowanie w czasie i częstotliwości (podobieństwo)
Je˙zeli x(t ) ˆ
= X (jω), to dla dowolnej stałej a > 0 zachodzi
x(at ) ˆ
=
1
a
X
µ j
ω
a
¶
.
(2.22)
Dowód:
F [x(at)] =
Z
∞
−∞
x(at ) e
−jωt
dt =
Z
∞
−∞
x(
τ)e
−j
ω
a
τ
d
τ
a
=
1
a
X
µ j
ω
a
¶
.
(2.23)
Twierdzenie o transformacie splotu
Je˙zeli
x(t ) ˆ
= X (jω) oraz
y(t ) ˆ
= Y (jω) ,
(2.24a)
to
Z
∞
−∞
x(t − τ)y(τ) dτ ˆ
= X (jω)Y (jω) .
(2.24b)
Udowodnijmy to:
F
½Z
∞
−∞
x(t − τ)y(τ) dτ
¾
=
Z
∞
−∞
·Z
∞
−∞
x(t − τ)y(τ) dτ
¸
e
−jωt
dt =
=
Z
∞
−∞
y(
τ)£
Z
∞
−∞
x(t − τ) e
−jωt
dt
¤ d
τ.
(2.25)
1
Wi ˛
ecej o transformacie Fouriera jedynki Heaviside’a napisano w podrozdziale 6.1.2 na stronie 176.
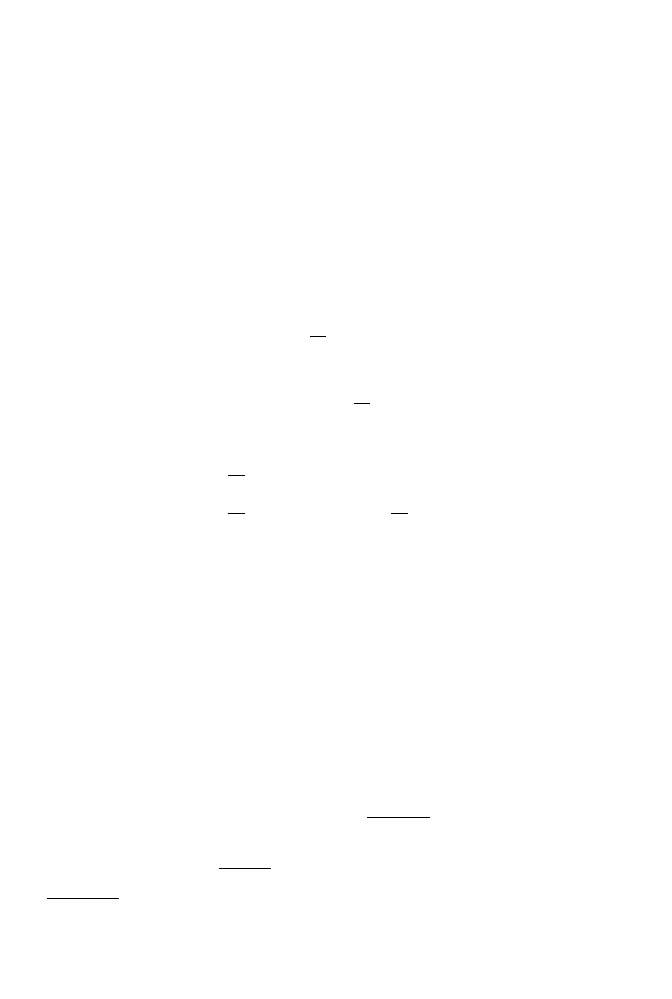
36
2. Transformacja Fouriera
Wprowadzaj ˛
ac now ˛
a zmienn ˛
a całkowania u = t −τ, mamy dt = du oraz t = u +τ, wobec
tego
F
½Z
∞
−∞
x(t − τ)y(τ)dτ
¾
=
Z
∞
−∞
y(
τ)
·Z
∞
−∞
x(u) e
−jω(u+τ)
dt
¸
d
τ =
=
Z
∞
−∞
y(
τ)e
−jωτ
d
τ
Z
∞
−∞
x(u) e
−jωu
du = X (jω)Y (jω) .
(2.26)
Wzór Parsevala
Je˙zeli
x(t ) ˆ
= X (jω) ,
(2.27a)
to
Z
∞
−∞
|x(t )|
2
dt =
1
2
π
Z
∞
−∞
|X (jω)|
2
d
ω.
(2.27b)
Spróbujmy to wykaza´c:
Z
∞
−∞
|x(t )|
2
dt =
Z
∞
−∞
x(t ) x
∗
(t ) dt =
Z
∞
−∞
x(t )
·
1
2
π
Z
∞
−∞
X
∗
(j
ω)e
−jωt
d
ω
¸
dt .
(2.28)
Zmieniaj ˛
ac kolejno´s´c całkowania, otrzymujemy
Z
∞
−∞
|x(t )|
2
dt =
1
2
π
Z
∞
−∞
X
∗
(j
ω)
·Z
∞
−∞
x(t ) e
−jωt
dt
¸
d
ω =
=
1
2
π
Z
∞
−∞
X
∗
(j
ω) X (jω)dω =
1
2
π
Z
∞
−∞
|X (jω)|
2
d
ω.
Wzór Parsevala posiada interpretacj ˛
e fizyczn ˛
a. Warto´s´c całki
R
∞
−∞
|x(t )|
2
dt mo˙ze by´c
traktowana jako energia zamieniona na ciepło na oporniku 1
Ω przy przepływie pr ˛adu
i = x(t ) w niesko ´nczenie wielkim przedziale czasowym. Zgodnie ze wzorem Parsevala
całka z kwadratu g ˛
esto´sci widmowej amplitudy równie˙z przedstawia energi ˛
e. Dlatego
mówi si ˛
e o rozkładzie energii w funkcji pulsacji, a wielko´s´c |X (jω)|
2
/(2
π) nazywana jest
g ˛
esto´sci ˛
a widmow ˛
a energii
2
.
Symetria dualna
Podobie ´
nstwo wzorów na proste i odwrotne przekształcenie Fouriera poci ˛
aga za so-
b ˛
a dualno´s´c oryginałów i ich obrazów. Zilustrujmy to przykładem. Znajd´zmy obraz
dla sygnału czasowego b ˛
ed ˛
acego pojedynczym impulsem prostok ˛
atnym, a nast ˛
epnie
znajd´zmy oryginał dla pojedynczego impulsu prostok ˛
atnego w dziedzinie cz ˛
estotliwo-
´sci:
x
1
(t ) =
(
1
dla
|t | < T
1
,
0
dla
T
1
< |t |
ˆ
= X
1
(j
ω) =
2 sin(
ωT
1
)
ω
(2.29a)
x
2
(t ) =
sin(
ω
0
t )
πt
ˆ
= X
2
(j
ω) =
(
1
dla
|ω| < ω
0
,
0
dla
ω
0
< |ω| .
(2.29b)
2
Je˙zeli całkowanie we wzorze (2.27b) odbywa si ˛
e wzgl ˛
edem cz ˛
estotliwo´sci f wyra˙zonej w hercach, a nie
wzgl ˛
edem pulsacji
ω wyra˙zonej w radianach na sekund˛e, to pomija si˛e współczynnik 1/(2π).
2.3. Wybrane własności przekształcenia Fouriera
37
Odpowiednie pary (oryginał i transformata) przedstawiono na rysunku 2.3. Łatwo za-
uwa˙zy´c symetri ˛
e, jaka wyst ˛
epuje w tych dwóch przekształceniach. B ˛
edzie ona wyst ˛
e-
powała tak˙ze w przypadku innych funkcji. Je˙zeli tylko we´zmiemy jedn ˛
a funkcj ˛
e i po-
liczymy jej transformat ˛
e, a nast ˛
epnie oryginał potraktujemy jako obraz i zastosujemy
do niego odwrotne przekształcenie, to otrzymane w ten sposób obraz i oryginał b ˛
ed ˛
a
do siebie podobne. Mo˙zemy to zapisa´c w nast ˛
epuj ˛
acej postaci:
x(t ) ˆ
= X (jω)
⇒
X (t ) ˆ
= 2πx(−ω).
(2.30)
1
(
)
X
jw
w
1
2T
1
/ T
p
1
T
1
T
-
t
1
( )
x t
1
1
2
(
)
X
jw
0
w
0
w
-
w
2
( )
x
t
0
/
w
p
0
/
p
w
t
Rysunek 2.3.
Podobie ´
nstwo oryginałów i obrazów
Sprzężenie i symetria
Je˙zeli
x(t ) ˆ
= X (jω) ,
(2.31a)
to
x
∗
(t ) ˆ
= X
∗
(−jω) .
(2.31b)
Mo˙zna to w prosty sposób udowodni´c. Obliczaj ˛
ac warto´s´c sprz ˛
e˙zon ˛
a X (j
ω), otrzymu-
jemy
X
∗
(j
ω) =
·Z
∞
−∞
x(t ) e
−jωt
dt
¸
∗
=
Z
∞
−∞
x
∗
(t ) e
j
ωt
dt .
(2.32)
Zamieniaj ˛
ac
ω na −ω, uzyskujemy
X
∗
(−jω) =
Z
∞
−∞
x
∗
(t ) e
−jωt
dt = F
©x
∗
(t )
ª .
(2.33)
Je´sli x(t ) jest rzeczywiste i x
∗
(t ) = x(t ), to na podstawie dwóch poprzednich wzorów
łatwo pokaza´c, ˙ze
X (−jω) = X
∗
(j
ω) oraz X
∗
(−jω) = X (jω) .
(2.34)
Je˙zeli przedstawimy X (j
ω) w postaci
X (j
ω) = Re{X (jω)} + jIm{X (jω)},
(2.35)

38
2. Transformacja Fouriera
to korzystaj ˛
ac ze wzoru (2.34) otrzymujemy nast ˛
epuj ˛
ace zale˙zno´sci (cały czas zakłada-
my, ˙ze x(t ) jest rzeczywiste):
Re{X (j
ω)} = Re{X (−jω)},
Im{X (j
ω)} = −Im{X (−jω)}.
(2.36)
Ze wzorów tych wynika tak˙ze, ˙ze g ˛
esto´s´c widmowa amplitudy jest funkcj ˛
a parzyst ˛
a,
a g ˛
esto´s´c widmowa fazy — funkcj ˛
a nieparzyst ˛
a. Wynik ten mo˙zna tak˙ze otrzyma´c w in-
ny sposób. Je´sli zapiszemy e
−jωt
= cos(ωt ) − j sin(ωt ), to transformata Fouriera sygnału
x(t ) mo˙ze by´c zapisana w postaci
F {x(t)} = X (jω) = X
1
(j
ω) − jX
2
(j
ω),
(2.37)
gdzie
X
1
(j
ω) =
Z
∞
−∞
x(t ) cos(
ωt)dt ,
X
2
(j
ω) =
Z
∞
−∞
x(t ) sin(
ωt)dt .
(2.38)
Wida´c, ˙ze funkcja X
1
(j
ω) jest parzysta, za´s X
2
(j
ω) nieparzysta wzgl˛edem ω. Zatem łatwo
pokaza´c, i˙z g ˛
esto´s´c widmowa amplitudy jest funkcj ˛
a parzyst ˛
a, a g ˛
esto´s´c widmowa fazy
funkcj ˛
a nieparzyst ˛
a wzgl ˛
edem
ω.
W tabeli 2.1 zebrano niektóre własno´sci transformaty Fouriera. Natomiast w tabe-
li 2.2 znalazły si ˛
e wybrane pary transformat. Wyliczenia poszczególnych transformat
Czytelnik mo˙ze znale´z´c w podrozdziale zawieraj ˛
acym przykłady.
Tabela 2.1.
Własno´sci transformaty Fouriera
Własność
Sygnał aperiodyczny
Transformata Fouriera
x(t )
,
y (t )
X (j
ω)
,
Y (j
ω)
Liniowo´s´c
a x(t ) + b y(t )
a X (j
ω) + b Y (jω)
Przesuni ˛
ecie w czasie
x(t − t
0
)
e
−jωt
0
X (j
ω)
Przesuni ˛
ecie w cz ˛
estotliwo´sci
e
j
ω
0
t
x(t )
X [j(
ω − ω
0
)]
Ró˙zniczkowanie oryginału
d
x(t )
d
t
j
ω X (jω)
Całkowanie oryginału
Z
t
−∞
x(
ζ)dζ
X (j
ω)
j
ω
+ π X (0) δ(ω)
Skalowanie w czasie
i cz ˛
estotliwo´sci (podobie ´
nstwo)
x(at ) , a > 0
1
a
X
µ j
ω
a
¶
Splot
Z
∞
−∞
x(t − τ) y(τ) dτ
X (j
ω)Y (jω)
Wzór Parsevala
Z
∞
−∞
|x(t )|
2
d
t =
1
2
π
Z
∞
−∞
|X (jω)|
2
d
ω

2.4. Gęstość widmowa sygnału na wyjściu układu liniowego
39
Tabela 2.2.
Wybrane pary transformat
Oryginał
Obraz
∞
X
k=−∞
c
k
e
jk
ω
0
t
2
π
∞
X
k=−∞
c
k
δ(ω − kω
0
)
e
j
ω
0
t
2
πδ(ω − ω
0
)
cos(
ω
0
t )
π[δ(ω + ω
0
) + δ(ω − ω
0
)]
sin(
ω
0
t )
j
π[δ(ω + ω
0
) − δ(ω − ω
0
)]
x(t ) = 1
2
πδ(ω)
δ(t)
1
1(
t )
1
j
ω
+ π δ(ω)
δ(t − t
0
)
e
−jωt
0
sin(
ω
0
t )
ω
0
t
X (j
ω) =
(π/ω
0
dla
|ω| < ω
0
,
0
dla
|ω| > ω
0
e
−ω
2
0
t
2
pπ
|ω
0
|
exp
µ
−
ω
2
4
ω
2
0
¶
e
−|ω
0
t |
2|ω
0
|
ω
2
0
+ ω
2
2.4. Gęstość widmowa sygnału na wyjściu układu liniowego
Przedstawiaj ˛
ac własno´sci przekształcenia Fouriera, pokazano, ˙ze splot dwóch sygna-
łów równy jest iloczynowi transformat Fouriera tych sygnałów. Korzystaj ˛
ac z tej wła-
sno´sci, mo˙zemy poda´c zwi ˛
azek pomi ˛
edzy transformat ˛
a Fouriera X (j
ω) sygnału na wej-
´sciu układu liniowego a transformat ˛
a Fouriera Y (j
ω) sygnału wyj´sciowego. Dany jest
on zale˙zno´sci ˛
a
Y (j
ω) = K (jω) X (jω),
(2.39)
gdzie K (j
ω) = |K (jω)|e
j arg[K (j
ω)]
jest charakterystyk ˛
a cz ˛
estotliwo´sciow ˛
a obwodu. Zwi ˛
azki
pomi ˛
edzy g ˛
esto´sciami widmowymi amplitudy i fazy sygnału wej´sciowego i wyj´sciowe-
go dane s ˛
a wzorami
|Y (jω)| = |K (jω)| |X (jω)| ,
(2.40a)
arg[Y (j
ω)] = arg[K (jω)] + arg[X (jω)].
(2.40b)
2.5. Przykłady
Przykład 2.1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Znajd´z transformat ˛
e Fouriera delty Diraca.

40
2. Transformacja Fouriera
Rozwi ˛
azanie. Korzystaj ˛
ac z definicji prostego przekształcenia Fouriera, otrzymujemy
F {δ(t)} =
Z
∞
−∞
δ(t)e
−jωt
dt = 1 .
.
Przykład 2.2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Znajd´z transformat ˛
e Fouriera sygnału jednostkowego
1(t ) =
(
0 ,
gdy
−∞ < t < 0 ,
1 ,
gdy
∞ > t > 0 .
Rozwi ˛
azanie. Niestety, w przypadku tej funkcji nie mo˙zemy skorzysta´c z twierdzenia
o obrazie pochodnej, gdy˙z nie spełnia ona zało˙ze ´
n. Wykorzystamy natomiast twier-
dzenie o obrazie całki. Skok jednostkowy mo˙ze by´c przedstawiony jako całka z delty
Diraca, tj. 1(t ) =
R
t
−∞
δ(ζ)dζ. W efekcie otrzymujemy
F {x(t)} =
1
j
ω
+ π δ(ω) .
.
Przykład 2.3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Znajd´z oryginał X (j
ω) = δ(ω).
Rozwi ˛
azanie. Korzystaj ˛
ac z definicji odwrotnego przekształcenia Fouriera, otrzymu-
jemy
x(t ) =
1
2
π
Z
∞
−∞
δ(ω)e
j
ωt
d
ω =
1
2
π
.
Dzi ˛
eki temu wynikowi mo˙zemy zapisa´c, jak wygl ˛
ada transformata Fouriera warto´sci
stałej:
F {1} = 2πδ(ω).
.
Przykład 2.4
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Znajd´z transformat ˛
e Fouriera sygnału okresowego x(t ) maj ˛
acego rozwini ˛
ecie w wy-
kładniczy szereg Fouriera.
Rozwi ˛
azanie. Sygnał x(t ) posiada rozwini ˛
ecie w szereg Fouriera, zatem
x(t ) =
∞
X
k=−∞
c
k
e
jk
ω
0
t
.
Znajd´zmy transformat ˛
e Fouriera tego sygnału. Skorzystamy w tym przypadku z twier-
dzenia o przesuni ˛
eciu obrazu
3
:
F {x(t)} = F ©
∞
X
k=−∞
c
k
e
−jkω
0
t
ª =
∞
X
k=−∞
2
πc
k
δ(ω − kω
0
) .
.
3
Chodzi tu o przesuni ˛
ecie obrazu funkcji w dziedzinie cz ˛
estotliwo´sci.

2.5. Przykłady
41
Przykład 2.5
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Znajd´z transformat ˛
e Fouriera funkcji x(t ) = cos(ω
0
t ).
Rozwi ˛
azanie. Zapiszmy funkcj ˛
e x(t ), korzystaj ˛
ac ze wzorów Eulera:
x(t ) = cos(ω
0
t ) =
e
−jω
0
t
+ e
j
ω
0
t
2
.
Korzystaj ˛
ac teraz z twierdzenia o przesuni ˛
eciu obrazu i wzoru na transformat ˛
e warto´sci
stałej, otrzymujemy ko ´
ncowy wzór:
F {cos(ω
0
t )} = πδ(ω + ω
0
) + πδ(ω − ω
0
) .
W tym miejscu warto przeanalizowa´c, jak wygl ˛
ada g ˛
esto´s´c widmowa funkcji typu y(t ) =
x(t ) cos(
ω
0
t ), w przypadku gdy znamy obraz funkcji x(t ). Łatwo pokaza´c, korzystaj ˛
ac
z twierdzenia o przesuni ˛
eciu obrazu, ˙ze je˙zeli
F {x(t)} = X (jω),
to
F {y(t)} = F
½
x(t )
2
e
−jω
0
t
+
x(t )
2
e
j
ω
0
t
¾
=
1
2
X [j(
ω + ω
0
)] +
1
2
X [j(
ω − ω
0
)] .
Wi ˛
ecej informacji na ten temat mo˙zna znale´z´c w rozdziale po´swi ˛
econym modulacji.
.
Przykład 2.6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Znajd´z transformat ˛
e Fouriera funkcji x(t ) = sin(ω
0
t ).
Rozwi ˛
azanie. Zapiszmy funkcj ˛
e x(t ) w innej postaci:
x(t ) = sin(ω
0
t ) =
e
j
ω
0
t
− e
−jω
0
t
2j
.
Korzystaj ˛
ac teraz z twierdzenia o przesuni ˛
eciu obrazu i wzoru na transformat ˛
e warto´sci
stałej, otrzymujemy ko ´
ncowy wzór:
F {sin(ω
0
t )} = πj δ(ω + ω
0
) − πj δ(ω − ω
0
) .
.
Przykład 2.7
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Znajd´z oryginał dla X (j
ω) danego wzorem
X (j
ω) =
π
ω
0
[1(
ω + ω
0
) − 1(ω − ω
0
)] .
Rozwi ˛
azanie. Korzystaj ˛
ac z definicji odwrotnego przekształcenia Fouriera, otrzymu-
jemy
x(t ) =
1
2
π
Z
ω
0
−ω
0
πe
j
ωt
ω
0
d
ω =
1
2jt
ω
0
e
j
ωt
¯
¯
¯
¯
ω
0
−ω
0
=
2j sin(
ω
0
t )
2j
ω
0
t
=
sin(
ω
0
t )
ω
0
t
.
Zatem
x(t ) =
sin(
ω
0
t )
ω
0
t
.
.
42
2. Transformacja Fouriera
Przykład 2.8
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Znajd´z transformat ˛
e Fouriera sygnału przedstawionego na rysunku 2.4.
t
b
a
a
-
b
-
( )
x t
A
Rysunek 2.4.
Sygnał
x(t ) z przykładu 2.8
Rozwi ˛
azanie. Mo˙zna oczywi´scie znale´z´c obraz zadanej funkcji, korzystaj ˛
ac ze wzoru
definiuj ˛
acego to przekształcenie. Spróbujmy jednak ułatwi´c sobie troch ˛
e doj´scie do
rozwi ˛
azania, wykorzystuj ˛
ac twierdzenie o obrazie zró˙zniczkowanej funkcji. Zró˙znicz-
kujmy dwukrotnie funkcj ˛
e x(t ). Zabieg ten został zilustrowany na rysunkach 2.5 i 2.6.
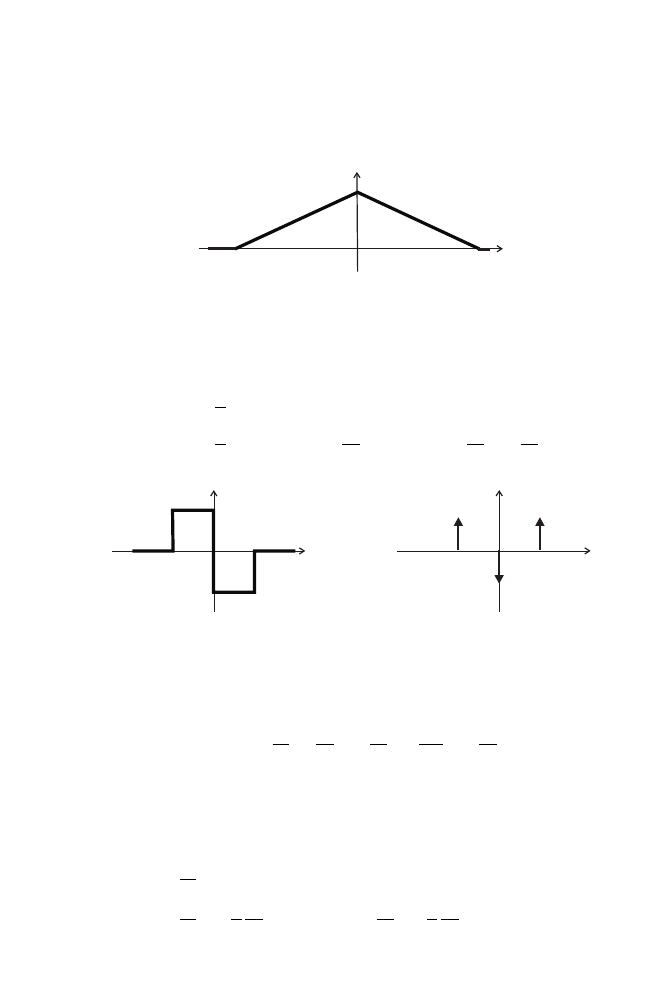
Druga pochodna składa si ˛
e z czterech impulsów Diraca. W prosty sposób mo˙zemy
znale´z´c obraz drugiej pochodnej.
F { ¨x(t)} =
A
a − b
F ©δ(t + a) − δ(t + b) − δ(t − b) + δ(t − a)ª
=
A
a − b
(e
j
ωa
− e
j
ωb
− e
−jωb
+ e
−jωa
) =
A
a − b
[cos(
ωa) − cos(ωb)].
t
b
a
a
-
b
-
/(
)
A
a
b
-
/(
)
A
a
b
-
-
( )
x t
&
Rysunek 2.5.
Pierwsza pochodna sygnału
x(t ) z przykładu 2.8
t
b
a
a
-
b
-
/(
)
A
a
b
-
/(
)
A
a
b
-
-
/(
)
A
a
b
-
-
/(
)
A
a
b
-
( )
x t
&&
Rysunek 2.6.
Druga pochodna sygnału
x(t ) z przykładu 2.8
Pami ˛
etaj ˛
ac, ˙ze
F { ¨x(t)} = (jω)
2
F {x(t)},
otrzymujemy
F {x(t)} = −
1
ω
2
A
a − b
[cos(
ωa) − cos(ωb)].
.
2.5. Przykłady
43
Przykład 2.9
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Znajd´z transformat ˛
e Fouriera sygnału x(t ) przedstawionego na rysunku 2.7.
( )
x t
A
t
e
e
-
0
Rysunek 2.7.
Sygnał
x(t ) z przykładu 2.9
Rozwi ˛
azanie. Zró˙zniczkujmy dwukrotnie funkcj ˛
e x(t ). Zabieg ten został zilustrowany
na rysunku 2.8. Druga pochodna składa si ˛
e z trzech impulsów Diraca. W prosty sposób
mo˙zemy znale´z´c obraz drugiej pochodnej:
F { ¨x(t)} =
A
ε
F ©δ(t + ε) − 2δ(t) + δ(t − ε)ª
=
A
ε
(e
j
ωε
−2 + e
−jωε
) =
2A
ε
[cos(
ωε) − 1] = −
4A
ε
sin
2
µ
ωε
2
¶
.
( )
x t
&
( )
x t
&&
/
A e
/
A e
-
e
e
-
t
e
e
-
/
A e
/
A e
2 /
A e
-
t
Rysunek 2.8.
Pierwsza i druga pochodna sygnału
x(t ) z przykładu 2.9
Pami ˛
etaj ˛
ac, ˙ze
F { ¨x(t)} = (jω)
2
F {x(t)},
otrzymujemy
F {x(t)} =
µ
−
1
ω
2
¶·
−
4A
ε
sin
2
µ
ωε
2
¶¸
=
4A
εω
2
sin
2
µ
ωε
2
¶
.
.
Przykład 2.10
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Oblicz oryginalny sygnał x(t ), którego widmo przedstawione jest na rysunku 2.9.
Rozwi ˛
azanie. Korzystaj ˛
ac z definicji odwrotnego przekształcenia Fouriera, mo˙zemy
zapisa´c
x(t ) =
1
2
π
Z
∞
−∞
X (j
ω)e
j
ωt
d
ω =
=
1
2
π
Z
0
−2A
π
A
1
2A
(2A + ω) e
j
ωt
d
ω +
1
2
π
Z
2A
0
π
A
1
2A
(2A − ω) e
j
ωt
d
ω.
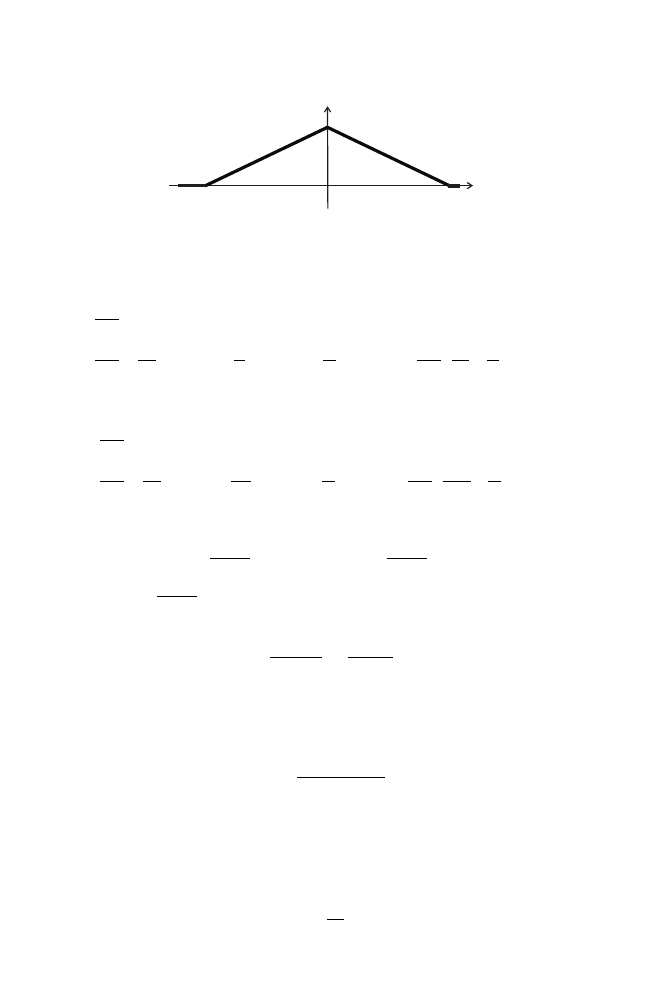
44
2. Transformacja Fouriera
0
(
)
X
jw
/ A
p
w
2 A
2 A
-
Rysunek 2.9.
Widmo sygnału
x(t ) z przykładu 2.10
Obliczmy warto´s´c pierwszej całki:
I
1
=
1
4A
2
Z
0
−2A
(2A + ω) e
j
ωt
d
ω =
=
1
4A
2
½· 2A
jt
e
j
ωt
¸
0
−2A
+
·
ω
jt
e
j
ωt
¸
0
−2A
+
· 1
t
2
e
j
ωt
¸
0
−2A
¾
=
1
4A
2
· 2A
jt
+
1
t
2
(1 − e
−j2At
)
¸
oraz drugiej:
I
2
=
1
4A
2
Z
2A
0
(2A − ω) e
j
ωt
d
ω =
=
1
4A
2
½· 2A
jt
e
j
ωt
¸
2A
0
+
· −ω
jt
e
j
ωt
¸
2A
0
−
· 1
t
2
e
j
ωt
¸
2A
0
¾
=
1
4A
2
· −2A
jt
−
1
t
2
(e
j2At
−1)
¸
.
W efekcie otrzymujemy
x(t ) = I
1
+ I
2
=
1
4(At )
2
(1 − e
−jAt
+1 − e
jAt
) =
1
2(At )
2
[1 − cos(2At )] =
=
1
2(At )
2
[sin
2
(At ) + cos
2
(At ) − cos
2
(At ) + sin
2
(At )].
Zatem
x(t ) =
sin
2
(At )
(At )
2
=
· sin(At )
At
¸
2
.
.
Przykład 2.11
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Okre´sli´c pulsacj ˛
e graniczn ˛
a idealnego filtru dolnoprzepustowego o wzmocnieniu w pa-
´smie przepuszczania równym 2, je˙zeli wiadomo, ˙ze po pobudzeniu sygnałem
x(t ) =
500 sin
2
(500t )
(500t )
2
energia sygnału na wej´sciu i wyj´sciu filtru jest taka sama.
Rozwi ˛
azanie. Na rysunku 2.10 przedstawiono g ˛
esto´s´c widmow ˛
a sygnału na wej´sciu
filtru X (
ω), wyj´sciu Y (ω) oraz charakterystyk˛e cz˛estotliwo´sciow ˛a filtru K (ω). Obliczmy
energi ˛
e sygnału na wej´sciu filtru. Zgodnie ze wzorem Parsevala mo˙zemy zapisa´c
E
x
=
Z
+∞
−∞
|x(t )|
2
dt =
1
2
π
Z
+∞
−∞
|X (ω)|
2
d
ω.
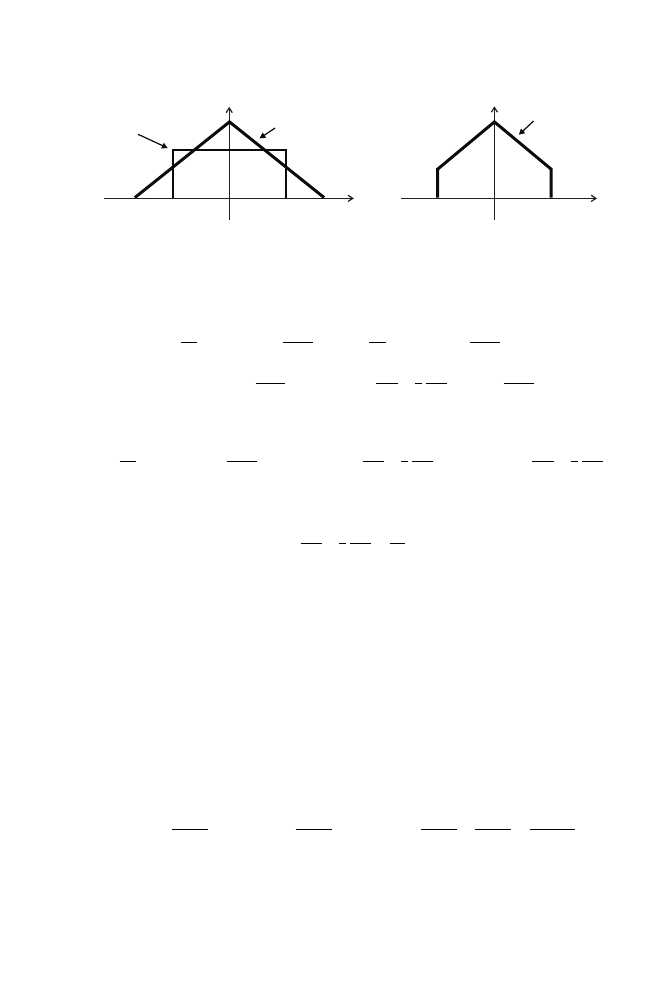
2.5. Przykłady
45
1000
-
g
w
-
g
w
1000
0
( )
K w
( )
X w
w
2
p
( )
Y w
2p
g
w
-
g
w
0
w
Rysunek 2.10.
G ˛
esto´sci widmowe
X (
ω) i Y (ω) oraz charakterystyka cz˛estotliwo´sciowa filtru
K (
ω)
W naszym przypadku
E
x
=
1
2
π
Z
0
−1000
·
π
µ
1 +
ω
1000
¶¸
2
d
ω +
1
2
π
Z
1000
0
·
π
µ
1 −
ω
1000
¶¸
2
d
ω =
= π
Z
0
−1000
µ
1 +
ω
1000
¶
2
d
ω = π
·
ω +
ω
2
10
3
+
1
3
ω
3
10
6
¸
0
−1000
=
π10
3
3
.
Energia sygnału na wyj´sciu filtru dana jest wzorem
E
y
=
1
2
π
2
Z
0
−ω
g
·
2
π
µ
1 +
ω
1000
¶¸
2
d
ω = 4π
·
ω +
ω
2
10
3
+
1
3
ω
3
10
6
¸
0
−ω
g
= 4π
µ
ω
g
−
ω
2
g
10
3
+
1
3
ω
3
g
10
6
¶
.
Zgodnie z warunkami zadania E
x
= E
y
, zatem
ω
g
−
ω
2
g
10
3
+
1
3
ω
3
g
10
6
=
1
12
10
3
.
Rozwi ˛
azuj ˛
ac to równanie, otrzymujemy
ω
g
≈ 91,4 rad/s.
.
Przykład 2.12
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Znajd´z transformat ˛
e Fouriera sygnału
x(t ) = e
−a|t |
,
a > 0 .
Rozwi ˛
azanie. Zgodnie z definicj ˛
a prostego przekształcenia Fouriera mo˙zemy zapisa´c
X (j
ω) =
Z
∞
−∞
e
−a|t |
e
−jωt
dt =
Z
0
−∞
e
at
e
−jωt
dt +
Z
∞
0
e
−at
e
−jωt
dt .
Zatem
X (j
ω) =
1
a − jω
e
t (a−jω)
¯
¯
¯
¯
0
−∞
−
1
a + jω
e
−t (a+jω)
¯
¯
¯
¯
∞
0
=
1
a − jω
+
1
a + jω
=
2a
a
2
+ ω
2
.
.
Przykład 2.13
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Wyznacz g ˛
esto´s´c widmow ˛
a impulsu prostok ˛
atnego przedstawionego na rysunku 2.11:
f (t ) = A[1(t + ε) − 1(t − ε)] .
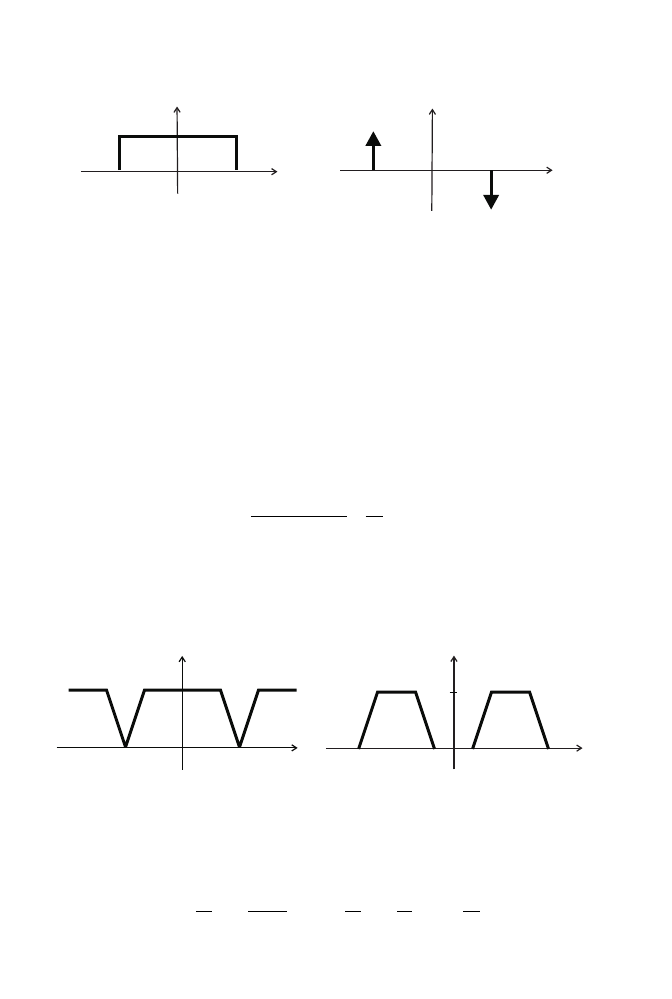
46
2. Transformacja Fouriera
( )
f t
A
e
e
-
t
e
e
-
t
( )
f t
&
(
)
A
t
d
e
+
(
)
A
t
d
e
-
-
Rysunek 2.11.
Sygnał
f (t ) z przykładu 2.13 oraz jego pierwsza pochodna
Rozwi ˛
azanie. Korzystaj ˛
ac z twierdzenia o transformacie funkcji przesuni ˛
etej w czasie,
znajdujemy transformat ˛
e Fouriera ˙
f (t ):
F { ˙f(t)} = A[F {δ(t + ε)} − F {δ(t − ε)}] = A(e
j
ωε
− e
−jωε
) .
Równocze´snie na podstawie twierdzenia o transformacie pochodnej funkcji czasowej
mamy
F { ˙f(t)} = jωF (ω).
Wobec tego
j
ωF (ω) = A(e
j
ωε
− e
−jωε
) .
W efekcie otrzymujemy
F (
ω) =
2A(e
j
ωε
− e
−jωε
)
2j
ω
=
2A
ω
sin(
ωε).
.
Przykład 2.14
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Sygnał x(t ) = (πt )
−1
sin(100t ) podano na dwa poł ˛
aczone kaskadowo filtry, których cha-
rakterystyki amplitudowe przedstawiono na rysunku 2.12, przy czym filtry te nie ob-
ci ˛
a˙zaj ˛
a si ˛
e wzajemnie. Oblicz energi ˛
e sygnału y(t ) na wyj´sciu układu.
-100
-60
-20
60
100
20
( )
A
K
w
w
-100
-60
-20
60
100
20
w
1
( )
B
K
w
Rysunek 2.12.
Charakterystyki amplitudowe filtrów z przykładu 2.14
Rozwi ˛
azanie. Na rysunku 2.13 przedstawiono g ˛
esto´sci widmowe sygnałów na wej´sciu
i wyj´sciu układu. Korzystaj ˛
ac ze wzoru Parsevala oraz uwzgl ˛
edniaj ˛
ac symetri ˛
e g ˛
esto´sci
widmowej sygnału na wyj´sciu układu, mo˙zemy obliczy´c szukan ˛
a energi ˛
e:
E
y
= 8
1
2
π
Z
40
20
µ
ω − 20
20
¶
2
d
ω = 8
1
2
π
Z
20
0
µ
ω
20
¶
2
d
ω =
80
3
π
.
.
2.5. Przykłady
47
-100
100
w
( )
X w
-100
-60
-20
20
60
100
w
( )
Y w
1
Rysunek 2.13.
G ˛
esto´sci widmowe sygnałów wej´sciowego i wyj´sciowego w przykładzie 2.14
Przykład 2.15
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Sygnał
x(t ) = A cos(Ωt )
sin(
ω
0
t )
ω
0
t
,
gdzie
Ω = 300 rad/s, ω = 100 rad/s, A = 200, podano na wej´scie idealnego filtru górno-
przepustowego o wzmocnieniu w pa´smie przepuszczania równym 2.
• Oblicz i narysuj g ˛
esto´s´c widmow ˛
a sygnału x(t ).
• Wyznacz pulsacj ˛
e graniczn ˛
a filtru, je˙zeli wiadomo, ˙ze energia sygnału y(t ) na
wyj´sciu filtru stanowi 25% energii sygnału wej´sciowego.
Rozwi ˛
azanie. G ˛
esto´s´c widmow ˛
a sygnału x(t ) przedstawiono na rysunku 2.14. Wyzna-
czono j ˛
a jako g ˛
esto´s´c widmow ˛
a sygnału cos(
Ωt), zmodulowanego sygnałem Sa(ω
0
t )
4
.
Analitycznie mo˙ze by´c ona zapisana w postaci
X (j
ω) = π[1(ω + 400) − 1(ω + 200) + 1(ω − 200) − 1(ω − 400)].
( )
X w
2p
[
]
0
Sa(
t)
F
w
w
-400
-300
-200
-100
0
100
200
300
400
Rysunek 2.14.
G ˛
esto´s´c widmowa sygnału
x(t ) z przykładu 2.15
Energi ˛
e sygnału x(t ), zgodnie ze wzorem Parsevala, mo˙zemy obliczy´c:
E
x
=
1
2
π
Z
−200
−400
(
π)
2
d
ω +
1
2
π
Z
400
200
(
π)
2
d
ω =
1
π
Z
400
200
(
π)
2
d
ω = 200π.
Natomiast energia sygnału y(t ) wynosi
E
y
=
1
π
Z
400
ω
g
(2
π)
2
d
ω = 4π(400 − ω
g
) .
4
Sa(
ω
0
t ) = (ω
0
t )
−1
sin(
ω
0
t ).

48
2. Transformacja Fouriera
Zgodnie z warunkami zadania E
y
= 0,25E
x
, zatem
4
π(400 − ω
g
) = 0,25 · 200π
Rozwi ˛
azuj ˛
ac to równanie, otrzymujemy
ω
g
= 387,5 rad/s
.
2.6. Literatura
[1] M. Krakowski, Elektrotechnika teoretyczna, Pa ´
nstwowe Wydawnictwo Naukowe,
Warszawa 1991.
[2] A. V. Oppenheim, R. W. Schafer, Cyfrowe przetwarzanie sygnałów, Wydawnictwa Ko-
munikacji i Ł ˛
aczno´sci, Warszawa 1979.
[3] A. V. Oppenheim, A. S. Willisky, Signals & Systems, Prentice Hall Inc., Upper Saddle
River, New Jersey 1997.
[4] A. Wojnar, Teoria sygnałów, Wydawnictwa Naukowo-Techniczne, Warszawa 1980.
Wyszukiwarka
Podobne podstrony:
Teoria sygnalów Wstep Wydanie II poprawione i uzupelnione
Programowanie Teoria i praktyka z wykorzystaniem C Wydanie II poprawione 2
Programowanie Teoria i praktyka z wykorzystaniem C Wydanie II poprawione
Finanse korporacyjne Teoria i praktyka Wydanie II finkor
Okablowanie strukturalne sieci Teoria i praktyka Wydanie II
Pilhofer M Teoria muzyki dla bystrzaków Wydanie II
Teoria muzyki dla bystrzakow Wydanie II temuby
informatyka okablowanie strukturalne sieci teoria i praktyka wydanie ii rafal pawlak ebook
więcej podobnych podstron