www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

P

RÓBNY

E

GZAMIN

M

ATURALNY

Z

M

ATEMATYKI

Z

ESTAW PRZYGOTOWANY PRZEZ SERWIS

WWW

.

ZADANIA

.

INFO

POZIOM PODSTAWOWY

2

KWIETNIA

2011

C

ZAS PRACY

: 170

MINUT

1

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Zadania zamkni˛ete

Z

ADANIE

1

(1

PKT

.)

Motor kosztował 4500 zł. Jego cen˛e obni ˙zono o 10%, a nast˛epnie cen˛e po tej obni ˙zce ponow-
nie obni ˙zono o 10%. Po tych obni ˙zkach motor kosztował
A) 3660 zł

B) 3705 zł

C) 3645 zł

D) 3600 zł

Z

ADANIE

2

(1

PKT

.)

Iloraz 16

−

4

:

1

64

2

jest równy

A) 2

−

28

B) 2

4

C) 2

−

4

D) 2

28

Z

ADANIE

3

(1

PKT

.)

Stosunek pól dwóch kół jest równy 16. Wynika st ˛ad, ˙ze promie ´n wi˛ekszego koła jest wi˛ekszy
od promienia mniejszego koła
A) o 16

B) o 4

C) 4 razy

D) 16 razy

Z

ADANIE

4

(1

PKT

.)

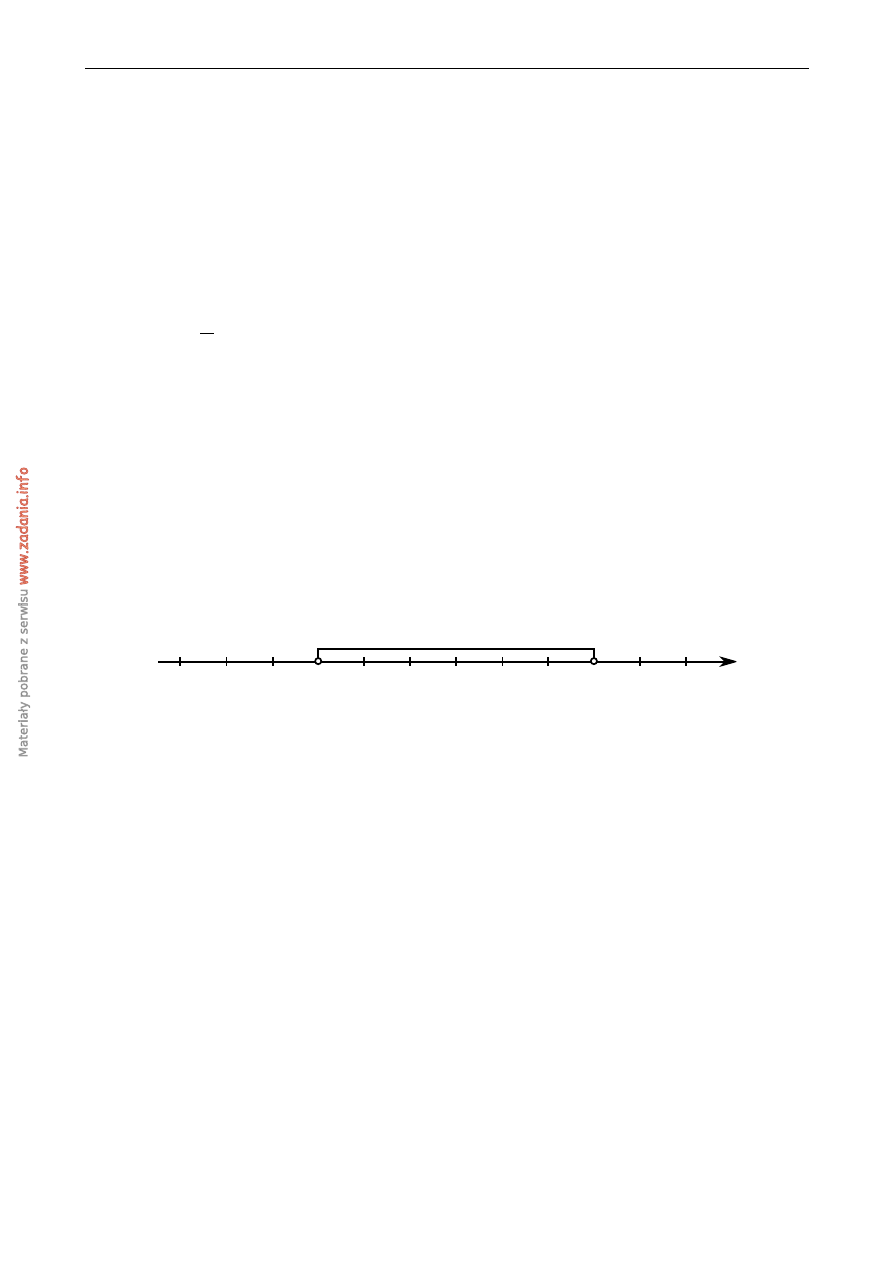
Wska ˙z nierówno´s´c, która opisuje przedział zaznaczony na osi liczbowej.

x

-2

-8

A)

|

x

+

5

| <

3

B)

|

x

−

5

| <

3

C)

|

x

−

5

| >

3

D)

|

x

+

5

| >

3

Z

ADANIE

5

(1

PKT

.)

Która z liczb jest równa 2?
A) log

2

2

B) log

4

2

C) log

2

4

D) log

2

1

Z

ADANIE

6

(1

PKT

.)

Iloczyn wielomianów W

(

x

) = −

5x

3

−

2 i P

(

x

) =

x

4

−

2x

2

−

1 jest wielomianem stopnia

A) 7

B) 3

C) 5

D) 6

Z

ADANIE

7

(1

PKT

.)

Ile rozwi ˛aza ´n rzeczywistych ma równanie 3x

4

−

5

=

0?

A) 4

B) 3

C) 2

D) 1

2

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

8

(1

PKT

.)

Do wykresu funkcji f

(

x

) =

x

2

−

2x

−

2 nale ˙zy punkt

A)

(−

1,

−

3

)

B)

(−

1, 1

)

C)

(−

1,

−

1

)

D)

(−

1,

−

2

)

Z

ADANIE

9

(1

PKT

.)

Wierzchołek paraboli y

=

x

2

−

4x

+

5 le ˙zy na prostej o równaniu

A) x

= −

2

B) x

=

2

C) x

=

4

D) x

= −

4

Z

ADANIE

10

(1

PKT

.)

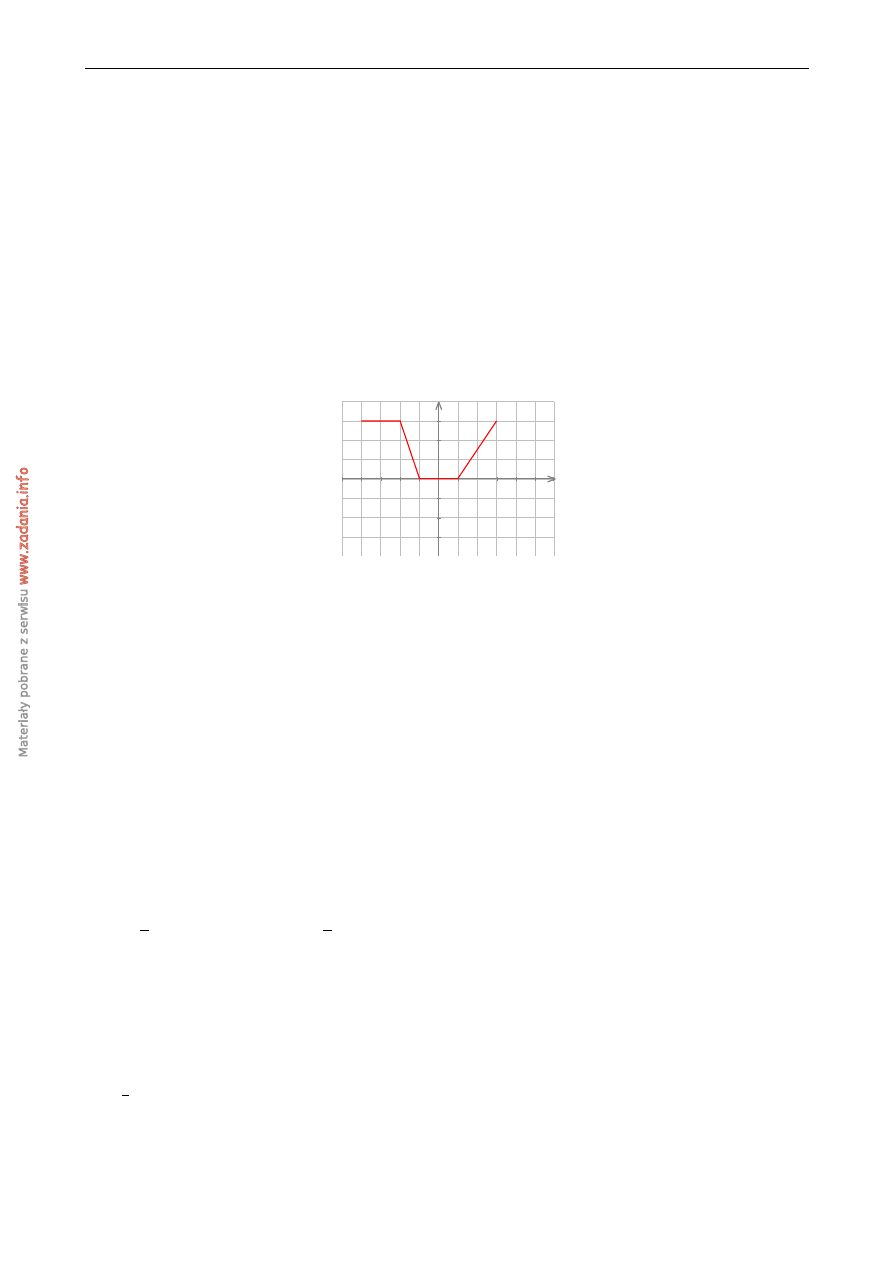
Maksymalny przedział, w którym funkcja h (rysunek poni ˙zej)

-4

-1

+3

x

-1

+1

+2

y

y=h(x)

jest malej ˛aca to
A)

h−

4,

−

1

i

B)

h−

2,

−

1

i

C)

h−

4, 1

i

D)

h−

2, 1

i

Z

ADANIE

11

(1

PKT

.)

Funkcja f okre´slona jest wzorem f

(

x

) =

(

x

−

2 dla x

>

1

−

x

dla x

<

1.

Ile miejsc zerowych ma ta funkcja?
A) 0

B) 1

C) 2

D) 3

Z

ADANIE

12

(1

PKT

.)

W malej ˛acym ci ˛agu geometrycznym

(

a

n

)

mamy: a

1

= −

2 i a

3

= −

6. Iloraz tego ci ˛agu jest

równy
A)

−

√

3

B)

√

3

C) -3

D) 3

Z

ADANIE

13

(1

PKT

.)

Punkt A

= (

2,

−

1

)

jest pocz ˛atkiem odcinka AB, gdzie S

= (−

1, 1

)

jest jego ´srodkiem. Punkt

B

, który jest ko ´ncem tego odcinka ma współrz˛edne

A)

1

2

, 0

B)

(−

4, 3

)

C)

(

1, 0

)

D)

(−

8, 6

)

3

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

14

(1

PKT

.)

Dany jest okr ˛ag o równaniu

(

x

+

4

)

2

+ (

y

−

7

)

2

=

36. Długo´s´c tego okr˛egu jest równa

A) 36π

B) 6π

C) 12π

D) 24π

Z

ADANIE

15

(1

PKT

.)

Pionowy słupek o wysoko´sci 60 cm rzuca cie ´n o długo´sci 90 cm. W tej samej chwili stoj ˛aca
obok wie ˙za rzuca cie ´n długo´sci 12 m. Jaka jest wysoko´s´c wie ˙zy?
A) 18 m

B) 8 m

C) 9 m

D) 16 m

Z

ADANIE

16

(1

PKT

.)

K ˛at α jest ostry i sin α

=

6

7

. Wówczas cos α jest równy

A)

13

49

B)

4

√

7

6

C)

√

13

7

D)

√

85

7

Z

ADANIE

17

(1

PKT

.)

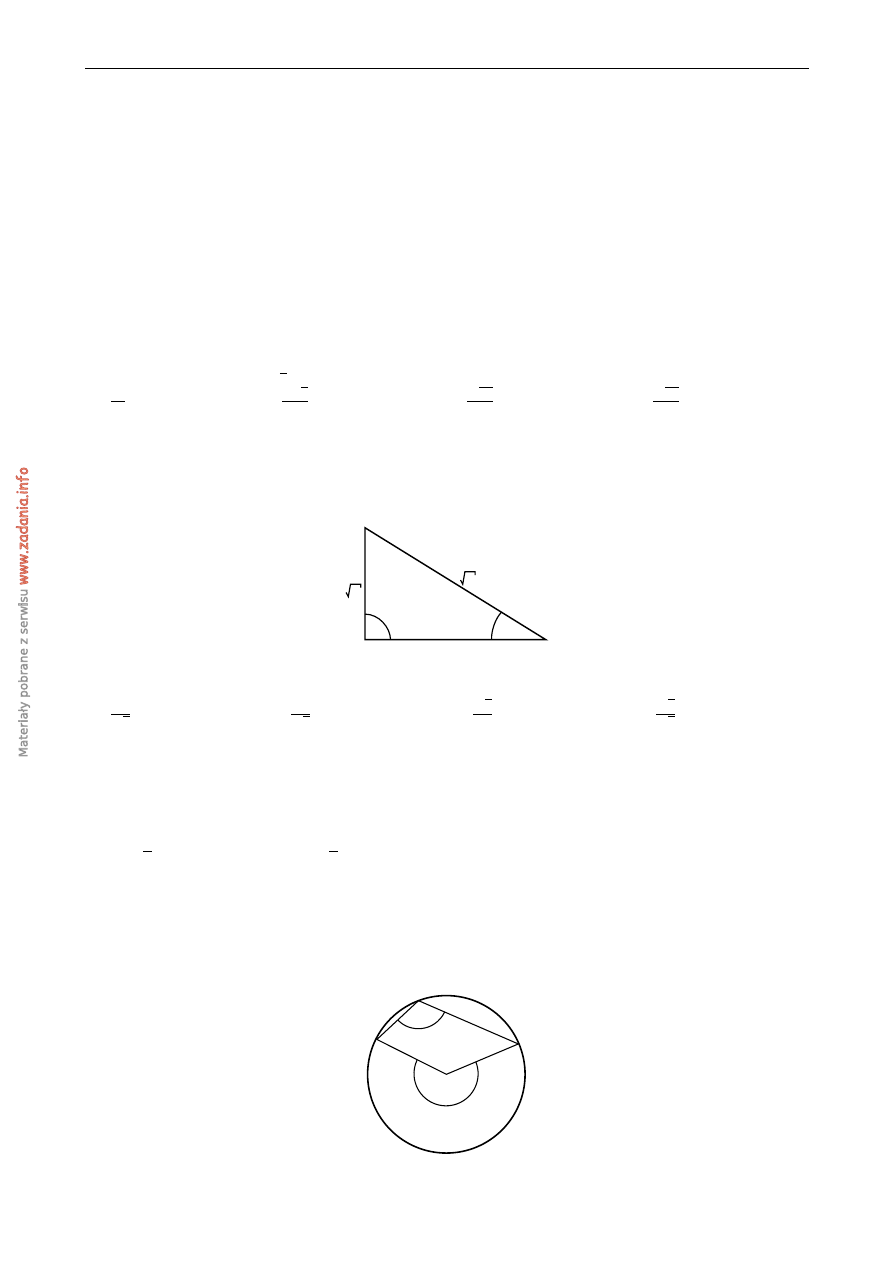
Dany jest trójk ˛at prostok ˛atny (patrz rysunek).

α

2

7

3

Wtedy tg α jest równy
A)

2

√

7

B)

2

√

3

C)

√

3

2

D)

√

3

√

7

Z

ADANIE

18

(1

PKT

.)

Punkty A

= (

4,

−

3

)

i B

= (−

2, 9

)

s ˛a wierzchołkami trójk ˛ata równobocznego ABC. Obwód

tego trójk ˛ata jest równy
A) 18

√

5

B) 6

√

5

C) 45

D) 54

Z

ADANIE

19

(1

PKT

.)

Punkty A, B i C le ˙z ˛a na okr˛egu o ´srodku S (zobacz rysunek).

260

o

A

B

C

S

4

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Miara zaznaczonego k ˛ata wpisanego ACB jest równa

A) 50

◦

B) 100

◦

C) 115

◦

D) 130

◦

Z

ADANIE

20

(1

PKT

.)

Które z równa ´n opisuje prost ˛a prostopadł ˛a do prostej o równaniu y

= −

3

5

x

+

3?

A) y

=

3

5

x

+

5

B) y

= −

3

5

x

+

3

C) y

=

5

3

x

+

3

D) y

=

5x

+

3

Z

ADANIE

21

(1

PKT

.)

O zdarzeniach losowych A i B zawartych w Ω wiadomo, ˙ze A

⊆

B

, P

(

A

) =

0, 2 i P

(

B

) =

0, 6. Wtedy
A) P

(

A

∪

B

) =

1

B) P

(

A

∪

B

) =

0, 2

C) P

(

A

∪

B

) =

0, 4

D) P

(

A

∪

B

) =

0, 6

Z

ADANIE

22

(1

PKT

.)

Pan Łukasz ma 3 marynarki, 8 par ró ˙znych spodni i 11 ró ˙znych koszul. Na ile ró ˙znych
sposobów mo ˙ze si˛e ubra´c, je´sli zawsze zakłada marynark˛e, spodnie i koszul˛e.
A) 280

B) 22

C) 132

D) 264

Z

ADANIE

23

(1

PKT

.)

Powierzchnia sze´scianu wynosi 96 cm

2

. Kraw˛ed´z tego sze´scianu ma długo´s´c

A) 4 cm

B) 5 cm

C) 5,5 cm

D) 6 cm

Z

ADANIE

24

(1

PKT

.)

Liczba ujemnych wyrazów ci ˛agu

(

a

n

)

okre´slonego wzorem a

n

=

1

3

n

−

2, gdzie n

>

1 jest

równa
A) 6

B) 5

C) 9

D) 7

Z

ADANIE

25

(1

PKT

.)

´Srednia arytmetyczna dziesi˛eciu liczb x, 3, 2, 4, 1, 5, 1, 4, 1, 5 jest równa 3. Wtedy

A) x

=

2

B) x

=

3

C) x

=

4

D) x

=

5

5

Z

ADANIE

26

(2

PKT

.)

Rozwi ˛a˙z nierówno´s´c x

2

+

3x

+

4

<

0.

Z

ADANIE

27

(2

PKT

.)

Uzasadnij, ˙ze je´sli

q

a

2

+

b

2

2

=

a

+

b

2

to a

=

b

.

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

6

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

28

(2

PKT

.)

Punkt M jest punktem wspólnym przek ˛atnych trapezu prostok ˛atnego ABCD. Punkt N jest
punktem wspólnym przek ˛atnej BD i wysoko´sci CE opuszczonej na dłu ˙zsz ˛a podstaw˛e AB.
Wyka ˙z, ˙ze

|

DM

|

2

= |

MN

| · |

MB

|

.

A

B

C

E

D

M

N

7

Z

ADANIE

29

(2

PKT

.)

Wyka ˙z, ˙ze trójk ˛at ABC o wierzchołkach A

= (−

3; 4

)

, B

= (−

7;

−

8

)

, C

= (

3; 2

)

jest prosto-

k ˛atny.

Z

ADANIE

30

(2

PKT

.)

Rozwi ˛a˙z równanie x

3

−

17x

2

+

2x

−

34

=

0.

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

8

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

31

(4

PKT

.)

Rzucamy dwa razy symetryczn ˛a sze´scienn ˛a kostk ˛a do gry. Oblicz prawdopodobie ´nstwo
otrzymania iloczynu oczek równego 6.

9

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

32

(6

PKT

.)

Po torze wodnym o długo´sci 10 km pływaj ˛a w kółko dwie łodzie motorowe, przy czym
druga z nich płynie z pr˛edko´sci ˛a o 5 km/h wi˛eksz ˛a od pr˛edko´sci pierwszej łodzi. Łodzie te
wystartowały z tego samego punktu i ponownie spotkały si˛e, gdy pierwsza z łodzi wyko-
nała pełne 3 okr ˛a˙zenia toru. Oblicz ´srednie pr˛edko´sci obu łodzi.

10

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´N Z

M

ATEMATYKI

Z

ADANIE

33

(5

PKT

.)

Wysoko´s´c ostrosłupa prawidłowego czworok ˛atnego jest równa 6. Kraw˛ed´z boczna jest na-
chylona do płaszczyzny podstawy pod k ˛atem 30

◦

. Oblicz obj˛eto´s´c tego ostrosłupa.

11