(LINIE PIERWIASTKOWE)
Transmitancja operatorowa otwartego układu regulacji z jednostkowym ujemnym sprzęŜeniem zwrotnym dana jest wzorem:
1
G
O = K ⋅ s( s + 2)( s + ) 5
a) Podaj obraz linii pierwiastkowych układu zamkniętego.
b) Określ krytyczne wzmocnienie K, przy którym układ zamknięty znajduje się na granicy stabilności oraz podaj odpowiadającą temu pulsację drgań nietłumionych.
Rozwią zanie
Niech:
m oznacza liczbę skończonych zer transmitancji układu otwartego G 0( s) , n oznacza liczbę jej biegunów.
Dla rozwaŜanej transmitancji G 0( s) zachodzi: m = 0 oraz n = 3.
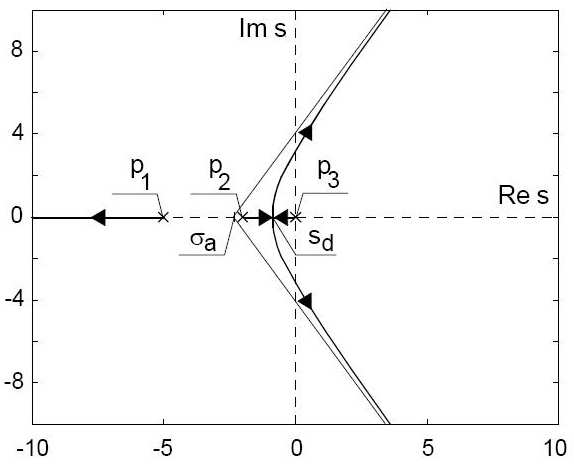
Biegunami G 0( s) są liczby: p 1=−5 , p 2 =−2 , p 3 = 0 .
Liczba asymptot, do których dąŜą linie pierwiastkowe wynosi n− m=3.
Kąty między asymptotami mają wartość: 2*180o/3=120o.
Kąty między asymptotami a osią rzeczywistą są równe ± 60o , 180o .
Odcięta σ punktu na osi rzeczywistej, z którego wychodzą asymptoty: a
n
∑ pi
i 1
σ
.
a =
=
= 2
− .333
n
Wspólną część linii pierwiastkowych oraz rzeczywistej osi płaszczyzny zespolonej stanowi prawostronnie domknięta półprosta leŜąca w lewo od bieguna p 1 oraz domknięty odcinek pomiędzy biegunami p 2 i p 3 .
Wynika stąd, iŜ punkt "odejścia" linii pierwiastkowych od osi rzeczywistej naleŜy do odcinka [ p 2, p 3].
Współrzędną punktu odejścia znajdujemy na podstawie charakterystycznego równania układu zamknię tego, wyznaczając maksymalną wartość parametru K, dla której bieguny układu zamknię tego są rzeczywiste.
Charakterystyczny wielomian W( s) rozwaŜanego układu ma postać W( s)= s3+7s2+10s+K
RóŜniczkując otrzymujemy:
W( s)= 3s2+14s+10
o następujących pierwiastkach:
s 1 =−0.8804 oraz s 2 =−3.7863.
_________________________________________________
1 _
_______________________________________________
Powered by xtoff®
lalik.krzysztof@wp.pl
Tylko pierwszy z nich wyznacza szukany punkt odejścia: sd = s 1 .
Zachodzi bowiem s 1=[ p 2, p 3].
Podstawiając s = sd w równaniu W( s) = 0 , otrzymujemy odpowiadającą temu punktowi wartość Kd wzmocnienia K : Kd = 4.0607
Krytyczną wartość wzmocnienia KKR , przy której układ zamknięty osiąga granicę
stabilnoś ci, obliczyć moŜna na podstawie równania charakterystycznego W( s) = 0 , kładąc s =
j w.
Postępując w ten sposób, uzyskujemy równanie jω 1
( 0
2
ω
ω
K
n
−
)
n
− 7 2 n + KR = 0
(1)
w którym ω oznacza pulsację odpowiednich drgań nietłumionych.
n
Przyrównując do zera urojoną część wyraŜenia po lewej stronie tego równania, otrzymujemy: rad
ω = 10
n
.
s
Z kolei, po podstawieniu pulsacji ω do równania (1), uzyskujemy równanie, ,z n
którego wyznaczamy krytyczną wartość wzmocnienia:
KKR.= 70
Tak uzyskany obraz linii pierwiastkowych pokazano na poniŜszym rysunku: _________________________________________________
2 _
_______________________________________________
Powered by xtoff®
lalik.krzysztof@wp.pl
(LINIE PIERWIASTKOWE)
Rozpatrzymy układ ze sprzęŜeniem zwrotnym
W(s)
E(s)
Regulator
U(s)
Obiekt
Y(s)
Kp
Go(s)
–
Transmitancja obiektu ma postać
K
G ( s)
0
=
0
s( s + )
1
Wyznaczyć połoŜenie pierwiastków układu zamkniętego ze względu na Kp.
Rozwią zanie
Wykorzystując przyjęte wcześniej formy zapisu m=0
b(s)=1
K0=1
K = Kp
n=2
a(s)=s2+s
pi = 0, -1
Charakterystyka połoŜenia pierwiastków jest graficznym przedstawieniem pierwiastków równania:
a( s) + Kb( s) = 0
czyli:
2
s + s + K = 0
Rozwiązania mają postać:
1
1− 4 K
s , s = − ±
1
2
2
2
_________________________________________________
3 _
_______________________________________________
Powered by xtoff®
lalik.krzysztof@wp.pl
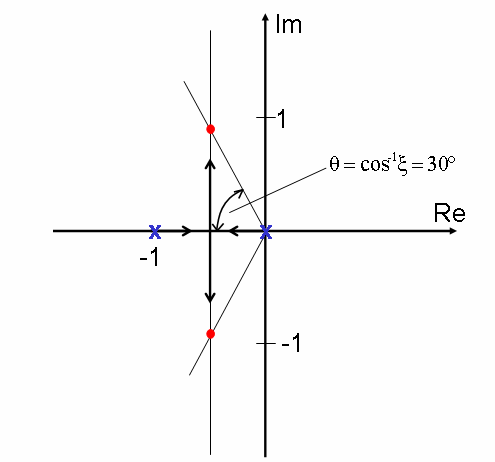
Szkic połoŜenia pierwiastków
1
Dla 0 ≤ K ≤
pierwiastki przyjmują wartości rzeczywiste z przedziału (-1,0).
4
1
1
Dla K =
istnieją dwa pierwiastki o wartościach równych −
4
2
1
1
Dla K >
pierwiastki są liczbami zespolonymi, których część rzeczywista ma wartość −
,
4
2
natomiast część urojona wzrasta proporcjonalnie do K .
Zmieniając wartość K moŜemy umiejscowić bieguny układu zamkniętego w dowolnych punktach naleŜących do charakterystyki pierwiastków.
_________________________________________________
4 _
_______________________________________________
Powered by xtoff®
lalik.krzysztof@wp.pl
(LINIE PIERWIASTKOWE)
RozwaŜmy transmitancję:
s + 1
G
O = K ⋅ s( s + 4)( 2
s + 2 s + 2)
które odpowiada równaniu charakterystycznemu W(s)=s( s + 4)( s 2 + 2 s + 2)+ K( s +1)= 0
Rozwią zanie
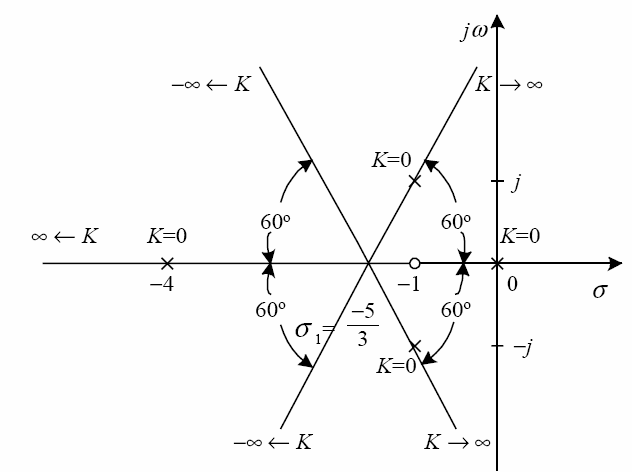
Konfiguracja zero-biegunowa pokazana jest na rysunku 4. Korzystając z poznanych własności linii pierwiastkowych, kiedy w równaniu charakterystycznym K zmienia się od −∞
do +∞ , wówczas:
1. K = 0: Punkty na linii pierwiastkowej w których K = 0 są biegunami transmitancji G( s) H( s): s = 0, s=−4, s=−1+ j oraz s=−1− j.
2. K = ± ∞: Punkty na linii pierwiastkowej w których K = ± ∞ są zerami transmitancji G( s) H( s): s = −1, s = ∞, s = ∞ oraz s = ∞.
3. Z równania charakterystycznego widać, Ŝe będą cztery linie pierwiastkowe, gdyŜ równanie to jest czwartego rzędu.
4. Linie pierwiastkowe są symetryczne względem osi liczb rzeczywistych.
5. PoniewaŜ liczba biegunów transmitancji G( s) H( s) jest większa od liczby zer transmitancji G( s) H( s) i róŜnica ta wynosi trzy ( n − m = 4 − 1 = 3 ), czyli kiedy K = ± ∞, wówczas linie pierwiastkowe zmierzają przy s = ∞ wzdłuŜ sześciu asymptot. Kąty asymptot przy K ≥ 0 są wyznaczane z równania
i
2 +
Θ =
1 ⋅1800, n ≠ m
i
n − m
gdzie i = 0, 1, 2, ..., n − m -1; 0
180
0
i = 0 ⇒ Θ =
= 60
0
3
0
540
0
i = 1 ⇒ Θ =
= 180
1
3
0
900
0
i = 2 ⇒ Θ =
= 300
2
3
Kąty asymptot przy K ≤ 0 są wyznaczane z równania: i
Θ = 2
⋅1800, n ≠ m
i
n − m
gdzie i = 0, 1, 2, ..., n − m -1; wynoszą odpowiednio: 0o , 120o oraz 240o .
_________________________________________________
5 _
_______________________________________________
Powered by xtoff®
lalik.krzysztof@wp.pl
6. Kąty przecięcia asymptot wyznaczane są ze wzoru n
m
∑ p − ∑ z
i
j
i=1
j
=
=1
σ
a
n − m
,gdzie
pi – bieguny transmitancji G( s) H( s)
zj - zera transmitancji G( s) H( s) (−4 − 1 − )
1 − (− )
1
σ =
1
4 −1
Asymptoty linii pierwiastkowych pokazane są na rysunku 4.
Rys. 4
_________________________________________________
6 _
_______________________________________________
Powered by xtoff®
lalik.krzysztof@wp.pl