PODSTAWOWE MIARY I OCENY PROJEKTÓW INWESTYCYJNYCH
PODSTAWOWE MIARY OCENY OPŁACALNOŚCI INWESTYCJI
Na rynku konkurencyjnym, jeśli dane przedsiębiorstwo nie chce pozostać w tyle w stosunku do swoich konkurentów, musi inwestować kaŜdego roku duŜe sumy kapitałów w
nowe przedsiębiorstwa (budowa nowej linii produkcyjnej, zakup drogiej maszyny, itd).
Takie inwestycje często określają losy firmy na długie lata. Dobre decyzje mogą zwiększyć zyski i spowodować wzrost wartości firmy, ale zła decyzja moŜe naruszyć zyski, obniŜyć wartość firmy, a nawet doprowadzić do jej bankructwa. Stąd tak istotne jest rozumienie i stosowanie odpowiednich miar do oceny opłacalności planowanych projektów inwestycyjnych.
Miary oceny projektów inwestycyjnych moŜemy podzielić na dwie kategorie:
• proste miary (nie uwzględniające wartości pieniądza w czasie):
- okres zwrotu.
• miary dochodowe (uwzględniające wartość pieniądza w czasie):,
- zdyskontowany okres zwrotu
- reguła wartości zaktualizowanej netto (NPV),
- wewnętrzna stopa zwrotu (IRR),
- zmodyfikowana wewnętrzna stopa zwrotu (MIRR).
OKRES ZWROTU
Przedsiębiorstwa preferują Ŝeby nakłady inwestycyjne związane z realizacją danego przedsięwzięcia zwróciły się w moŜliwie najkrótszym terminie. Stąd często stosowaną miarą jest okres zwrotu, który odpowiada na pytanie:
po upływie jakiego czasu suma wpływów pienięŜnych zrówna się z początkowymi nakładami?
Metoda okresu zwrotu pozwala na dokonanie wyboru, spośród rozpatrywanych projektów
inwestycyjnych takiego wariantu, który umoŜliwia najszybsze odzyskanie początkowych nakładów.
Ćwiczenie:
Jaki jest okres zwrotu dla projektu, którego przepływy pienięŜne znajdują się w tabeli obok (kiedy skumulowane nadwyŜki przekroczą nakłady)
Uwaga: jako pierwszy okres proszę potraktować rok 1.
Przepływy
Skumulowane przypływy
Skumulowana nadwyŜka
Rok
pienięŜne (tys.
pienięŜne (tys. PLN)
inwestycji początkowej (tys. PLN)
PLN)
0
(2000)
(2000)
0
1
500
(1500)
500
2
500
(1000)
1000
3
400
(600)
1400
4
800
200
2200
5
300
500
2500
6
200
700
2700
- 1 -
Rozwiązanie:
Zwrot początkowych nakładów nastąpi w trakcie 4 roku. Zakładając równomierne rozłoŜenie nadwyŜki finansowej w trakcie tego roku, okres zwrotu wyniesie:
Okres zwrotu = 3 lata + [(2000 – 1400)] 12 miesięcy = 3 lata 9 miesięcy
W naszym przykładzie policzyliśmy okres zwrotu obejmujący jedynie czas, który upływa od momentu zakończenia realizacji przedsięwzięcia (ponoszenia nakładów) do chwili zrównowaŜenia nakładów z nadwyŜkami finansowymi. Czasami do wyliczenia okresów zwrotu włącza się okres ponoszenia nakładów.
Inna modyfikacja moŜe polegać na załoŜeniu, Ŝe nakłady poniesione na zakup ziemi oraz na zgromadzenie niezbędnego kapitału obrotowego zostaną w pełni odzyskane przy końcu funkcjonowania przedsięwzięcia, a zwrotowi podlega jedynie kwota stanowiąca róŜnicę między tymi nakładami.
Cechy okresu zwrotu z inwestycji:
-
ogólna miara przepływów pienięŜnych (płynności) ale nie zyskowności (wartość zwrotu);
-
łatwość zastosowania;
-
preferencja dla szybko zwracających się przedsięwzięć – zmniejszenie ryzyka
czasu trwania projektu;
-
nie uwzględnione są zmiany wartości pieniądza w czasie;
-
nie uwzględnione okresy po osiągnięciu zwrotu;
-
obliczenie nie zawsze moŜliwe.
Wniosek – zastosowanie okresu zwrotu:
-
szybko zmieniająca się technologie, gospodarka nieustabilizowana, utrudniona,
długoterminowa projekcja przepływów pienięŜnych;
-
uŜyteczna jako wstępna ocena projektów (pomocnicza do metod dochodowych).
ZDYSKONTOWANY OKRES ZWROTU
Zasada postępowania jest taka sama jak w przypadku okresu zwrotu z tym, Ŝe do analizy bierze się przepływy po zdyskontowaniu na dzień analizy. Do dyskontowanie uŜywana jest stopa zwrotu analizowanych projektów charakteryzujących się zbliŜonym ryzykiem do danego projektu (koszt alternatywny).
Zasada zdyskontowanego zwrotu nakładów stawia następujące pytanie:
Ile okresów musi trwać projekt aby miał sens z punktu widzenia wartości
zaktualizowanej?
Ta modyfikacja zasady zwrotu odpiera zarzut przykładania równej wagi do wszystkich przepływów
pienięŜnych
przed
upływem
okresu
zwrotu.
JednakŜe
zasada
zdyskontowanego zwrotu, podobnie jak zasada zwrotu nie bierze pod uwagę przepływów
pienięŜnych, które następują po tym okresie.
Zastosowanie:
podobnie jak w przypadku dwóch poprzednich metod jako metoda pomocnicza.
- 2 -
WARTOŚĆ ZAKTUALIZOWANA NETTO – NPV
Formułę na liczenie NPV moŜna przedstawić następująco:
n
NPV =
∑ CFi
i
i=0 1
( + k)
gdzie:
CFi- strumień pienięŜny netto spodziewany w roku t,
k – stopa dyskontowa ,
n – czas Ŝycia projektu.
Badane przedsięwzięcie rozwojowe jest opłacalne jeŜeli NPV > 0 lub NPV = 0.
Dodatnia wartość NPV oznacza, Ŝe stopa rentowności przedsięwzięcia jest wyŜsza od stopy granicznej określonej poprzez przyjętą do projektu stopę dyskonta. Stąd kaŜda inwestycja charakteryzująca się NPV > 0 (w skrajnym przypadku NPV = 0) moŜe być zrealizowana gdyŜ przyniesie firmie określone korzyści finansowe, a więc podniesie jej wartość.
Ujemna wartość NPV świadczy o niŜszej od granicznej stopie rentowności
przedsięwzięcia. Jego realizacja będzie zatem nie opłacalna z punktu widzenia interesów właścicieli przedsiębiorstwa.
Procedury postępowania w przypadku oceny projektu inwestycyjnego metodą NPV:
-
naleŜy oszacować początkowe nakłady inwestycyjne oraz przygotować prognozę
przepływów pienięŜnych jakie dane przedsięwzięcie wygeneruje w czasie swego
trwania,
-
naleŜy ustalić stopę dyskontową – powinna ona odzwierciedlać równo wartość
pieniądza w czasie jak i ryzyko związane z realizacją rozpatrywanego
przedsięwzięcia (koszt alternatywny – oczekiwana stopa zwrotu z projektu o
porównywalnym ryzyku),
-
wykorzystując alternatywny koszt kapitału naleŜy zdyskontować przyszłe
przepływu pienięŜne wynikające z przedsięwzięcia suma zdyskontowanych
przepływów pienięŜnych nazywana jest wartością zaktualizowaną NPV**,
-
wartość zaktualizowaną netto (NPV) obliczamy obejmując odejmując od wartości zaktualizowanej przepływów pienięŜnych (PV) kwotę inwestycji (I),
-
naleŜy przystąpić do realizacji przedsięwzięcia jeŜeli jego wartość zaktualizowana netto jest większa lub równa zero (NPV > 0 lub NPV = 0)
WYMAGANA STOPA ZWROTU
Ćwiczenie:
Firma rozwaŜa zakup jednej z dwóch maszyn o róŜnych parametrach technicznych. Cena
obu maszyn jest jednakowa i wynosi 15 mln PLN. Oczekiwane wpływy pienięŜne z uŜytkowaniem maszyn wyglądają następująco (dane w tys. PLN).
Rok 1
Rok 2
Rok 3
Super
9000
6500
4000
DeLuxe
6500
6500
6500
- 3 -
JeŜeli wymagana stopa zwrotu wynosi 10% rocznie, który wariant jest bardziej opłacalny?
Rozwiązanie:
Super
9000
6500
4000
PV =
−
+
=
+
+
=
=
1 + 1
,
0
(1+ )1
,
0
2
(1+ ) 818 1 5 36 9 300 4 1 6554
1
,
0
3
NPV = PV – I = 16554 – 15000 = 1554
DeLuxe:
6500
6500
6500
1
1
PV =
+
+
=
⋅
−
=
=
1 + 1
,
0
(1+ )1
,
0
2
(1+ ) 6500
1
,
0
3
1
,
0
1
,
0 ⋅ (1 +
)
6
500·](1
0 7
,51
) 1
6165
1
,
0
2
NPV = PV – I = 16165 – 15000 = 1165
Obliczanie zaktualizowanej wartości netto oparte jest na załoŜeniu, Ŝe uzyskiwane w poszczególnych latach przepływy będą inwestowane po takiej samej stopie jak stopa dyskontowa uŜyta do wyliczenia NPV.
Rys.1.
- 4 -
WEWNĘTRZNA STOPA ZWROTU – IRR
Wewnętrzna stopa zwrotu (internal rate of return) to stopa procentowa, przy której obecna wartość strumieni wydatków pienięŜnych jest równa obecnej wartości strumieni wpływów pienięŜnych. Jest to więc taka stopa dyskontowa, przy której wartość zaktualizowana netto ocenionego projektu jest równa zero.
IRR = stopa dyskontowa przy której NPV = 0
IRR pokazuje bezpośrednio stopę rentowności badanych przedsięwzięć. Pojedyncze przedsięwzięcie rozwojowe jest opłacane wówczas, gdy jego wewnętrzna stopa zwrotu jest wyŜsza od (w skrajnym przypadku równa) od stopy granicznej będącej najniŜszą moŜliwą do zaakceptowania przez inwestora stopą rentowności.
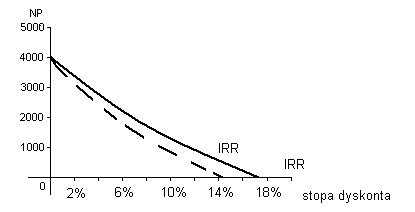
Rys.2.
Sposoby wyznaczania IRR:
-
przy uŜyciu arkusza kalkulacyjnego lub kalkulatora finansowego,
-
odczytywanie z wykresu,
-
obliczanie ze wzoru (daje wartość przybliŜoną).
NPV
IRR = A
A
+
⋅ (B − A)
NPV − NPV
A
B
gdzie:
A – poziom stopy dyskonta, przy którym NPV > 0,
B – poziom stopy dyskonta, przy którym NPV < 0,
NPVA – poziom NPV obliczony na podstawie stopy A,
NPVB – poziom NPV obliczony na podstawie stopy B.
- 5 -
Główna wada IRR obliczanie wewnętrznej stopy zwrotu oparte jest na załoŜeniu, Ŝe uzyskiwane w poszczególnych latach przepływy pienięŜne będą reinwestowane po takiej samej stopie, jak IRR. ZałoŜenie to moŜe okazać się nie moŜliwe do zrealizowania w praktyce.
Wewnętrzna stopa zwrotu liczona jest przy załoŜeniu, Ŝe uzyskiwane z projektu przepływy pienięŜne reinwestowane są po stopie procentowej równej IRR. Jest to załoŜenie trudne do zrealizowania w praktyce w szczególności jeśli firma realizuje projekt o wyŜszej rentowności od rentowności uzyskiwanej ze swojej dotychczasowej
działalności. Niedogodność tę próbuje wyeliminować tzw. zmodyfikowana wewnętrzna stopa zwrotu modified internal rate of return – MIRR.
MIRR zakłada, Ŝe uzyskiwane z projektu przepływy pienięŜne reinwestowane są po stopie równej kosztowi kapitału firmy.
Procedura wyliczenia MIRR polega na:
-
obliczeniu wartości końcowej przepływów pienięŜnych generowanych przez projekt
stosując do kapitalizowania koszt kapitału przedsiębiorstwa,
-
mając wartość końcową przepływów i wartość początkową (nakłady inwestycyjne)
oraz znając liczbę okresów projektu (lat) przy uŜyciu arkusza kalkulacyjnego wyliczamy zmodyfikowaną wewnętrzną stopę zwrotu projektu (MIRR).
Projekt inwestycyjny przyjmuje się do realizacji gdy zmodyfikowane wewnętrzna stopa zwrotu przewyŜsza koszt kapitału, czyli:
MIRR > k
KOSZT KAPITAŁU FIRMY A WYMAGANA STOPA ZWROTU Z PROJEKTU
Zarówno koszt kapitału firmy (WACC) uŜywany do dyskontowania przepływów
pienięŜnych całej firmy jak i wymagana stopa zwrotu z projektu uŜywana do dyskontowania przepływów pienięŜnych z danego projektu zaleŜą od:
-
źródeł finansowania (kapitał własny czy obcy),
-
oprocentowania kredytu,
-
wysokości podatku dochodowego,
-
rentowności osiąganej z inwestowania w alternatywne przedsięwzięcia (o
podobnym ryzyku),
-
ryzyka związanego z inwestowaniem na danym rynku.
Koszt kapitału zaangaŜowanego w dany projekt i średni waŜony koszt kapitału (WACC) są sobie równe tylko wówczas, kiedy ryzyko nowego projektu jest takie samo jak ryzyko operacyjne związane z dotychczasową działalnością firmy, a struktura finansowania projektu odpowiada strukturze finansowania całej firmy.
Mówimy, Ŝe jest to projekt typowy dla danej firmy. Tylko wówczas do dyskontowania przepływów pienięŜnych związanych z danym projektem moŜemy uŜywać średni waŜony
koszt kapitału (WACC) w szczególnym przypadku kiedy dla takiego projektu NPV = 0
zachodzi zaleŜność:
WACC = IRR
Dla projektów nietypowych, np. wchodzenie na nowe rynki naleŜy uŜyć kosztu kapitału odpowiadającego alternatywnemu uŜyciu kapitału w przedsięwzięciach o podobnym ryzyku.
- 6 -