DYNAMIKA BRYŁY SZTYWNEJ – PRZYKŁADOWE ZADANIA

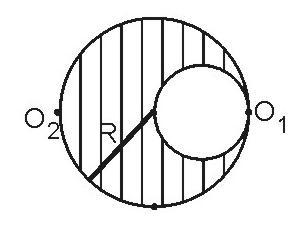
1. Wyznacz moment bezwładności wyciętego krążka względem osi obrotu O

. Masa pełnego krążka jest równa

1 i O2

M, a

promień R:

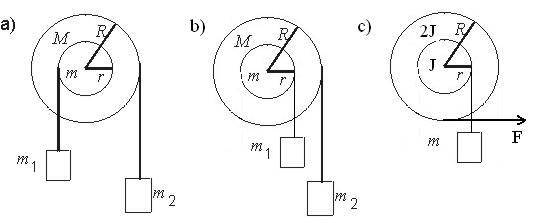
2. Wyznacz przyspieszenia liniowe mas i przyspieszenie kątowe bloczka:

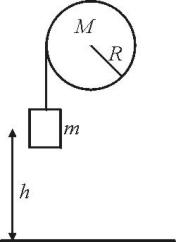
3. Na bęben o promieniu R i masie M nawinięto sznurek do którego przywiązano ciężar o masie m. Ciężar znajduje się na

wysokości h. W pewnej chwili ciężar został puszczony i zaczął się opuszczać. Po jakim czasie ciężar dotknie ziemi?

4. Ciężka szpula z nawiniętą nicią stoi na płaszczyźnie poziomej po której może się toczyć bez poślizgu. Obliczyć

przyspieszenie a środka masy szpulki oraz siłę tarcia T, jeśli do nici przyłożono siłę F w kierunku równoległym do

płaszczyzny. Masa szpulki m, moment bezwładności względem osi szpulki I , promień wewnętrzny

0

r, zewnętrzny R.

Rozważyć trzy przypadki:

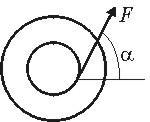
5. Ciężka szpula z nawiniętą nicią do której przyłożono siłę F leży na płaszczyźnie poziomej. W którą stronę i z jakim

przyspieszeniem liniowym będzie poruszać się szpula w zależności od kąta między kierunkiem siły działającej na nić a

płaszczyzną. Szpula porusza się ruchem obrotowym bez poślizgu. Masa szpulki m, moment bezwładności względem osi

szpulki I , promień wewnętrzny

0

r, zewnętrzny R.

6. Kula i cienka obręcz, o masie m i promieniu R zaczynają staczać się bez poślizgu z równi o kącie nachylenia a z wysokości

h. Znaleźć ich przyspieszenia liniowe i kątowe oraz prędkość u podnóża równi.

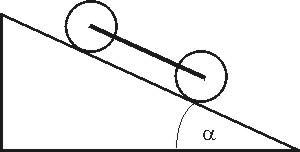
7. Z jakim przyspieszeniem liniowym i kątowym staczają się bez poślizgu kula i walec (kula i cienkościenna rura, walec i

obręcz), których środki połączono sztywnym prętem, z równi o kącie nachylenia . Jaką wartość mają siły tarcia? Masa

kuli i walca jest równa m a ich promienie R.

8. Z wysokości h stacza się bez poślizgu walec i kula. Która z brył będzie obracać się z większą częstotliwością u podnóża

równi i ile razy większą? Kąt nachylenia równi , masa kuli i walca m, promienie R. Oblicz stosunek energii kinetycznych

ruchu postępowego i obrotowego.

9. Ile czasu będzie się staczać bez poślizgu kula (walec, obręcz) o masie m i promieniu R z równi o kącie nachylenia , z

wysokości h.

10. Z wysokości h stacza się bez poślizgu walec. W drugim przypadku ta sama bryła zsuwa się bez tarcia. W którym

przypadku walec będzie miał większą prędkość u podnóża równi i ile razy większą? Kąt nachylenia równi , masa walca

m, promień R.

11. Na równię o kącie nachylenia zaczyna wtaczać się bez poślizgu walec (kula, cienkościenna rura), poruszający się przy

początku równi z prędkością v. Obliczyć drogę jaką przebędzie walec (kula, rura) do chwili zatrzymania się.

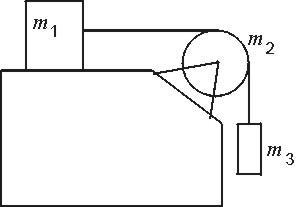
12. Z jakim przyspieszeniem opuszcza się masa m 1 w sytuacji jak na rysunku? Dany jest współczynnik tarcia k. Blok obraca

się pod działaniem nici. Promień bloku jest równy R.

13. Znaleźć użyteczną moc silnika wprawiającego w ruch platformę w kształcie kołowej tarczy o masie 200 kg i promieniu

2m, na brzegu której stoi człowiek o masie 70 kg, jeżeli wiadomo, że platforma osiąga częstotliwość obrotów 1 Hz w

czasie 40 s.

14. Kulka o masie m lecąca poziomo z prędkością v uderzyła w koniec pręta o masie M i długości L i odbiła się od niego 50 %

swojej prędkości. O jaki maksymalny kąt odchyli się pręt? Ile ciepła wydzieli się w wyniku tego zderzenia? Oś na której

zawieszony jest pręt przechodzi przez koniec pręta i pręt może obracać się wokół niej.

15. Dwie tarcze o masach m 1 i m 2 i promieniach r 1 i r 2 wirują wokół tej samej osi (prostopadłej do obydwu tarcz) z częstotliwościami f 1 i f 2. W pewnej chwili tarcze zsunęły się i zlepiły. Z jaką częstotliwością końcową wirują tarcze i ile

wydzieliło się ciepła? Tarcze wirują: a) w tym samym kierunku; b) w kierunkach przeciwnych.

16. Ze studni za pomocą kołowrotu podnoszone jest wiadro z wodą o masie 12 kg. W chwili gdy wiadro znajduje się na

wysokości 6 m nad powierzchnią wody, oswobodzono rączkę kołowrotu i wiadro zaczęło opuszczać się w dół. Znaleźć

prędkość liniową rączki kołowrotu w chwili uderzenia wiadra o powierzchnię wody, jeżeli odległość rączki od osi obrotu

jest równa 35 cm, promień wału kołowrotu 10 cm, a jego masa 18 kg. Zaniedbać ciężar liny na której zawieszone jest

wiadro.

17. Koło zamachowe o masie M przymocowane jest współśrodkowo do krążka o promieniu r i masie m. Krążek wprawiany

jest w ruch obrotowy za pomocą opuszczającego się w dół ciężarka o masie 3 m przywiązanego do nawiniętego na krążek

sznurka. Po jakim czasie częstość obrotów koła zamachowego będzie równa f? Przyjąć, że cała masa koła zamachowego

rozłożona jest na jego obwodzie w odległości R od osi obrotu.

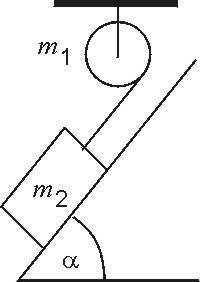
18. Do końca cienkiej, nierozciągliwej nici, nawiniętej na walcowy blok o promieniu r i masie m 1 przyczepiono ciało o masie

m , które znajduje się na równi pochyłej o kącie nachylenia

2

(jak na rysunku). Jaką drogę przebędzie ciało po równi w

czasie t, jeżeli współczynnik tarcia jest równy k. Ciało początkowo spoczywa, tarcie na osi bloku można zaniedbać.

19. Tarcza o masie 200 g i promieniu 50 cm wiruje z częstotliwością 2 Hz. Na środku tarczy siedzi mysz o masie 150 g. Oblicz

częstotliwość obrotów, gdy mysz przejdzie na brzeg taczy.

20. Oblicz moment bezwładności:

a) kuli o masie 500g i średnicy 6 cm względem osi stycznej do kuli

b) pręta o masie 1 kg i długości 80 cm względem osi prostopadłej do pręta przechodzącej w odległości 10 cm od jego

końca.

21. Znaleźć hamujący moment siły, który może zatrzymać w czasie 10 s koło zamachowe o masie 20 kg i promieniu 0.4m,

obracające się z częstotliwością 5 Hz. Założyć, że masa rozłożona jest na obwodzie. Obliczyć pracę wykonaną przy

zatrzymaniu koła.

22. Z gwiazdy o masie 4*1030 kg, promieniu 106 km i okresie wirowania 105 s w czasie wybuchu supernowej zostaje

odrzuconych w przestrzeń kosmiczną 90% masy. Z pozostałej masy powstaje gwiazda neutronowa o promieniu 100 km.

Odrzucona masa nie unosi momentu pędu. Oblicz okres wirowania gwiazdy neutronowej oraz gęstość gwiazdy przed i po

wybuchu.

23. Na brzegu karuzeli w kształcie obracającej się wokół osi tarczy o promieniu 0.8 m i masie 20 kg znajduje się dziecko o

masie 35 kg odpychające się od ziemi z szybkością 1m/s. Oblicz, z jaką częstotliwością będzie wirować karuzela, gdy

dziecko dojdzie do środka karuzeli (załóż, że masa dziecka znajduje się wtedy 10 cm od środka). Moment bezwładności

pozostałych elementów karuzeli wynosi 0.6 kg m2.

24. Człowiek próbuje unieść do góry masę 400 kg. W tym celu wziął pręt o długości 2 m i podsunął go 30 cm pod masę.

Oblicz jaką siłą musi zadziałać człowiek.

25. Oszacuj, jaką siłą działa Twój biceps, gdy podnosisz ręką 1 kg cukru.

26. Na dolny koniec wędki o długości 4 m i masie 300 g (przyjmij, że masa jest rozłożona równomiernie) nasunięto rękojeść

korkową o długości 50 cm i masie 80 g i w odległości 25 cm od końca przykręcono kołowrotek o masie 450 g. Oblicz, w

którym miejscu wędkarz musi trzymać wędkę, aby najmniej męczyć rękę.

27. Kolarz ma do dyspozycji koło pełne, w kształcie płaskiego krążka o masie 400 g i średnicy 70 cm, na które zakłada cienką

oponę o masie 100 g i koło złożone z obręczy o masie 150 g i średnicy 70 cm oraz 32 szprych o masie 9 g każda, na które

założona jest taka sama opona. Oblicz momenty bezwładności kół, stosunek momentów sił, które muszą zadziałać na koła

aby w tym samym czasie osiągnęły tą samą częstotliwość i stosunek prac, jakie trzeba wykonać, aby zatrzymać te koła.

Wymień wady i zalety stosowania tych kół.