


Algo
rytmy
i
struktury
danych
materiaªy
¢wiczenio
w
e
Studia
dzienne
PJWSTK
SPRA
WDZIAN
I
I
I
Imi¦
i
nazwisk
o:
Nr
indeksu:
Nr
grup
y:
Uw
aga!
Spra
wdzian
jest
testem
wielokrotnego wyb
oru,
gdzie
wszystkie
mo»liw
e
k
om
binacje
o
dp
o
wiedzi
s¡
dopuszczalne
(tj.
zaró
wno
wszystkie
o
dp
o
wiedzi
p
opra
wne,
cz¦±¢
o
dp
o
wiedzi
p
opra
wna
jak
i
brak
o
dp
o
wiedzi
p
opra
wn
yc
h).
P
opra
wne
o
dp
o
wiedzi
nale»y
zaznaczy¢,
z
lew
ej
stron
y
k
artki,
sym
b
olem
+.
Natomiast
sym
b
ol
-
jak
i
brak
sym
b
olu
przy
o
dp
o
wiedzi
oznacza
o
dp
o
wied¹
niep
opra
wn¡.
Pytanie
jest
uznane
za
p
opra
wnie
rozwi¡zane
(tj.
+1pkt)
wtedy
i
t
ylk
o
wtedy
gdy
wszystkie
jego
o
dp
o
wiedzi
zaznaczone
s¡
p
opra
wnie.
yczym
y
p
o
w
o
dzenia
...
1.
Które
z
p
oni»szyc
h
zda«
jest
za
wsze
pra
wdziw
e
w
dziedzinie
sªo
wnik
ó
w:
empty (d) ⇔ empty (delete (insert (insert (d, e) , e) , e)) (a)
[]
,
¬member (insert (delete (d, e) , e) , e) (b)
[]
,
member (d, e) ⇒ ¬member (delete (d, e) , e) (c)
[+]
.
T
2.
Niec
h
b
¦dzie
drzew
em
BST
p
o
wstaªym
przez
k
olejne
wsta
wianie
wierzc
hoªk
ó
w
o
et
ykietac
h
1, 7, 3, 2, 5, 8 do pocz¡tkowo pustej struktury, wtedy: T
3
(a)
[]
k
orzeniem
drzew
a
jest
wierzc
hoªek
o
et
ykiecie
,
T
1, 7, 3, 2, 5, 8
(b)
[+]
rezultatem
dziaªania
algorytm
u
PreOrder
dla
drzew
a
jest
ci¡
g
et
ykiet
,
1
T
(c)
[]
usuni¦cie
wierzc
hoªk
a
o
et
ykiecie
z
drzew
a
wymaga
okre±lenia
jego
b
ezp
o±redniego
nast¦pnik
a
w
rozw
a»an
ym
drzewie.
T
3.
Niec
h
b
¦dzie
drzew
em
A
VL
p
o
wstaªym
przez
k
olejne
wsta
wianie
wierzc
hoªk
ó
w
o
et
ykietac
h
1, 7, 3, 2, 5, 8 do pocz¡tkowo pustej struktury, wtedy: T
5
(a)
[]
k
orzeniem
drzew
a
jest
wierzc
hoªek
o
et
ykiecie
,
T
2, 1, 3, 5, 8, 7
(b)
[]
rezultatem
dziaªania
algorytm
u
P
ostOrder
dla
drzew
a
jest
ci¡
g
et
ykiet
,
3
T
(c)
[+]
usuni¦cie
wierzc
hoªk
a
o
et
ykiecie
z
drzew
a
wymaga
okre±lenia
jego
b
ezp
o±redniego
p
oprzednik
a/nast¦pnik
a
w
rozw
a»an
ym
drzewie.
T
n
n > 106
4.
Niec
h
b
¦dzie
drzew
em
A
VL
skªada
j¡cym
si¦
z
wierzc
hoªk
ó
w,
gdzie
,
wtedy:
√
member
T
n
(a)
[+]
k
oszt
op
eracji
na
drzewie
jest
nie
wi¦kszy
ni»
p
oró
wna«
et
ykiet
wierzc
hoª-
k
ó
w
drzew
a,
insert
T
6
(b)
[]
realizacja
op
eracji
w
drzewie
mo»e
sp
o
w
o
do
w
a¢
wyk
onanie
wi¦cej
ni»
-ciu
co
na
jwy»ej
p
o
dw
ó
jn
yc
h
rotacji,
delete
T
(c)
[]
realizacja
op
eracji
dla
p
ewnego
wierzc
hoªk
a
drzew
a
nie
mo»e
sp
o
w
o
do
w
a¢
wyk
o-
6
nania
wi¦cej
ni»
-ciu
co
na
jwy»ej
p
o
dw
ó
jn
yc
h
rotacji.
T
n
d
5.
Niec
h
drzew
o
binarne
b
¦dzie
implemen
tacj¡
-elemen
to
w
ego
sªo
wnik
a
,
wtedy
zªo»ono±¢
czaso
w
a
op
eracji:
member
d
O (lg n)
T
(a)
[+]
dla
sªo
wnik
a
jest
,
je»eli
jest
drzew
em
A
VL,
insert
d
Θ (lg n)
T
(b)
[]
dla
sªo
wnik
a
jest
,
je»eli
jest
drzew
em
BST,
delete
d
Ω (1)
T
(c)
[+]
dla
sªo
wnik
a
jest
,
je»eli
jest
drzew
em
A
VL.
1
P
a
w
eª
Remb
elski



Algo
rytmy
i
struktury
danych
materiaªy
¢wiczenio
w
e
Studia
dzienne
PJWSTK
6.
Które
z
p
oni»szyc
h
zda«
jest
za
wsze
pra
wdziw
e
w
dziedzinie
k
olejek
prioryteto
wyc
h:
min (pq) = min (insert (pq, min (pq))) (a)
[+]
,
min (pq) 6= min (insert (delmin (pq) , min (pq))) (b)
[]
,
empty (pq) ⇒ empty (delmin (insert (pq, e))) (c)
[+]
.
H
106
T
7.
Niec
h
b
¦dzie
-elemen
to
wym
k
op
cem
binarn
ym
zaimplemen
to
w
an
ym
w
drzewie
binarn
ym
,
wtedy:
T
lg 106
(a)
[+]
wysok
o±¢
drzew
a
jest
rz¦du
,
√
T
106
(b)
[]
drzew
o
ma
co
na
jwy»ej
wierzc
hoªk
ó
w
w
ewn¦trzn
yc
h,
T
1
(c)
[+]
liczba
wierzc
hoªk
ó
w
li±ci
na
ostatnim
p
oziomie
drzew
a
jest
ró
wna
co
na
jmniej
.
α = 0, 4, 1, 2, 5
8.
Rozw
a»m
y
ci¡
g
liczb
,
wtedy:
α
(a)
[]
tablica
reprezen
tuj¡ca
k
opiec
binarn
y
ut
w
orzon
y
z
elemen
tó
w
ci¡
gu
przez
k
olejne
wysta-
[0, 1, 2, 4, 5]
wianie
elemen
tó
w
do
p
o
cz¡tk
o
w
o
pustego
k
op
ca
ma
p
osta¢
,
α
(b)
[]
tablica
reprezen
tuj¡ca
k
opiec
binarn
y
ut
w
orzon
y
z
elemen
tó
w
ci¡
gu
przez
zastoso
w
anie
[0, 1, 2, 4, 5]
szybkiej
pro
cedury
budo
wy
k
op
ca
(tj.
HeapConstruct) ma
p
osta¢
,
α
(c)
[+]
tablica
reprezen
tuj¡ca
k
opiec
binarn
y
ut
w
orzon
y
z
elemen
tó
w
ci¡
gu
przez
zastoso
w
anie
[0, 2, 1, 4, 5]
szybkiej
pro
cedury
budo
wy
k
op
ca
(tj.
HeapConstruct) ma
p
osta¢
.
n
9.
Rozw
a»m
y
ci¡
g
liczb
naturaln
yc
h,
do
którego
zastoso
w
ano
algorytm
HeapSort,
wtedy:
Ω (n)
(a)
[+]
k
oszt
budo
wy
k
op
ca
binarnego
wynosi
,
O (n lg n)
(b)
[+]
k
oszt
rozebrania
k
op
ca
binarnego
wynosi
,
(c)
[+]
algorytm
HeapSort
jest
opt
ymaln
ym
algorytmem
sortuj¡cym
przez
p
oró
wnania.
H
2, 3, 4, 5, 6
10.
Rozw
a»m
y
k
opiec
binarn
y-drzew
o
p
o
wstaªy
przez
k
olejne
wsta
wianie
liczb
do
p
o
cz¡t-
k
o
w
o
pustej
struktury
,
wtedy:
6, 5, 4, 3, 2
(a)
[]
et
ykiet
y
drzew
a
o
dczytane
w
p
orz¡dku
P
ostOrder
t
w
orz¡
ci¡
g
,
insert (H, 1) min (H) (b)
[+]
je»eli
wyk
onam
y
ci¡
g
op
eracji
,
,
to
et
ykiet
y
drzew
a
o
dczytane
w
5, 3, 6, 1, 4, 2
p
orz¡dku
InOrder
t
w
orz¡
ci¡
g
,
insert
H
(c)
[+/]
k
oszt
op
eracji
na
strukturze
jest
rz¦du
linio
w
ego
wzgl¦dem
liczb
y
wierzc
hoªk
ó
w
drzew
a.
H
6, 5, 4, 3, 2
11.
Rozw
a»m
y
k
opiec
binarn
y-drzew
o
p
o
wstaªy
przez
k
olejne
wsta
wianie
liczb
do
p
o
cz¡t-
k
o
w
o
pustej
struktury
,
wtedy:
2, 3, 6, 4, 5
(a)
[+]
et
ykiet
y
drzew
a
o
dczytane
w
p
orz¡dku
PreOrder
t
w
orz¡
ci¡
g
,
delmin (H) delmin (H) (b)
[+]
je»eli
wyk
onam
y
ci¡
g
op
eracji
,
,
to
et
ykiet
y
drzew
a
o
dczytane
w
6, 4, 5
p
orz¡dku
InOrder
t
w
orz¡
ci¡
g
,
delmin
H
(c)
[+]
k
oszt
op
eracji
na
strukturze
jest
rz¦du
linio
w
ego
wzgl¦dem
wysok
o±ci
drzew
a.
G
n
12.
Rozw
a»m
y
graf
p
eªn
y
z
w
agami
skªada
j¡cy
si¦
z
wierzc
hoªk
ó
w,
wtedy:
G
O (n)
(a)
[]
k
oszt
pami¦cio
wy
macierzy
s¡siedzt
w
a
grafu
jest
rz¦du
,
G
Θ (n)
(b)
[]
k
oszt
pami¦cio
wy
tablicy
list
incydencji
grafu
jest
rz¦du
,
G
(c)
[+]
k
oszt
pami¦cio
wy
macierzy
s¡siedzt
w
a
grafu
jest
rz¦du
k
osztu
pami¦cio
w
ego
tablicy
list
G
incydencji
grafu
.
2
P
a
w
eª
Remb
elski


Algo
rytmy
i
struktury
danych
materiaªy
¢wiczenio
w
e
Studia
dzienne
PJWSTK
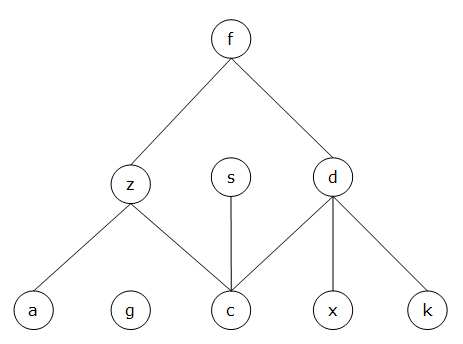
G = (V, E)
13.
Rozw
a»m
y
graf
przedsta
wion
y
na
p
oni»szym
rysunku,
wtedy:
(a)
[+]
k
olejno±¢
o
dwiedzania
wierzc
hoªk
ó
w
grafu
algorytmem
DFS
jest
zgo
dna
z
p
orz¡dkiem
a, z, f, d, x, k, c, s a
je»eli
wierzc
hoªkiem
starto
wym
jest
wierzc
hoªek
,
(b)
[]
k
olejno±¢
o
dwiedzania
wierzc
hoªk
ó
w
grafu
algorytmem
DFS
jest
zgo
dna
z
p
orz¡dkiem
z, s, d, f, x, k, s, c c
je»eli
wierzc
hoªkiem
starto
wym
jest
wierzc
hoªek
,
(c)
[+]
maksymalna
wysok
o±¢
stosu
p
omo
cniczego
w
algorytmie
DFS
zastoso
w
an
ym
do
wierz-
s
3
c
hoªk
a
starto
w
ego
jest
ró
wna
.
G = (V, E)
14.
Rozw
a»m
y
graf
z
zadania
13-tego,
wtedy:
(a)
[+]
k
olejno±¢
o
dwiedzania
wierzc
hoªk
ó
w
grafu
algorytmem
BFS
jest
zgo
dna
z
p
orz¡dkiem
f, d, z, c, k, x, a, s f
je»eli
wierzc
hoªkiem
starto
wym
jest
wierzc
hoªek
,
(b)
[+]
k
olejno±¢
o
dwiedzania
wierzc
hoªk
ó
w
grafu
algorytmem
BFS
jest
zgo
dna
z
p
orz¡dkiem
x, d, c, f, k, s, z, a x
je»eli
wierzc
hoªkiem
starto
wym
jest
wierzc
hoªek
,
O (|V | + |E|) (c)
[+]
zªo»ono±¢
czaso
w
a
algorytm
u
BFS
dla
rozw
a»anego
grafu
jest
rz¦du
.
G
G
15.
Niec
h
b
¦dzie
p
ewn
ym
grafem
skiero
w
an
ym,
wtedy
algorytm
sorto
w
ania
top
ologicznego
grafu
:
(a)
[]
dziaªa
p
opra
wnie
wtt
w,
gdy
graf
ten
jest
grafem
sp
ó
jn
ym,
(b)
[]
dziaªa
p
opra
wnie
wtt
w,
gdy
graf
ten
jest
grafem
z
w
agami,
O (|V |)
V
(c)
[]
ma
zªo»ono±¢
rz¦du
,
gdzie
jest
zbiorem
wierzc
hoªk
ó
w
rozw
a»anego
grafu.
3
P
a
w
eª
Remb
elski


Algo
rytmy
i
struktury
danych
materiaªy
¢wiczenio
w
e
Studia
dzienne
PJWSTK
16.
Zapis
auten
t
ycznej
rozmo
wy
radio
w
ej
przepro
w
adzonej
mi¦dzy
ameryk
a«skim
okr¦tami
a
Kanadyj-
czyk
ami.
Miaªa
ona
miejsce
w
pa¹dzierniku
1995r.
u
wybrze»y
No
w
ej
F
unlandii.
• Kanadyjczycy: Prosz¦ o zmian¦ kursu o 15 stopni na poªudnie w celu unikni¦cia kolizji.
• Amerykanie: Radzimy wam zmieni¢ kurs o 15 stopni na póªnoc, aby unikn¡¢ kolizji.
• Kanadyjczycy: To niemo»liwe. To wy b¦dziecie musieli zmieni¢ kurs o 15 stopni na poªudnie, ab
y
unikn¡¢
k
olizji.
• Amerykanie: Mówi kapitan okr¦tu wojennego Stanów Zjednoczonych. Powtarzam ponownie: wy
zmie«cie
kurs.
• Kanadyjczycy: Nie. Powtarzam: zmie«cie kurs, aby unikn¡¢ kolizji.
• Amerykanie: Mówi kapitan lotniskowca USS "Lincoln" - drugiego pod wzgl¦dem wielko±ci okr¦tu
b
o
jo
w
ego
ameryk
a«skiej
marynarki
w
o
jennej
ot
y
atlan
t
yc
kiej.
T
o
w
arzysz¡
nam
trzy
niszczyciele, trzy
kr¡»o
wniki
i
wiele
inn
yc
h
okr¦tó
w
wsp
omagania.
Domagam
si¦,
ab
y±cie
to
wy
zmienili
kurs
o
15
stopni
na
p
óªno
c.
W
inn
ym
przypadku
p
o
dejmiem
y
k
on
trdziaªania
w
celu
obron
y
grup
y!
• Kanadyjczycy: Mówi latarnia morska: wasz wybór!
Jak
sk
o«czyªa
si¦
o
w
a
historia:
(a)
dobrze,
(b)
¹le,
(c)
tego
nie
wiedz¡
na
w
et
na
jstarsi
górale.
4
P
a
w
eª
Remb
elski



