Próba ścisła
rozciągania metali.
Opracował:
XXXXXXXX
studia inŜynierskie zaoczne wydział mechaniczny
semestr V
Gdańsk 2001 r.
Cel ćwiczenia.
Celem ćwiczenia jest doświadczalne wyznaczenie:
- Umownej granicy proporcjonalności, określających największe napręŜenie do którego stosowane jest prawo Hook’a
- Modułu spręŜystości postaciowe (modułu Younga)
- Umownej granicy spręŜystości
- Umownej granicy plastyczności w przypadku braku wyraźnej granicy plastyczności.
Podstawowe definicje.
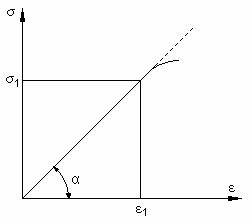
Moduł Younga E jest to stosunek napręŜenia σ1 do odpowiadającego mu wydłuŜenia jednostkowego ε1 co zapisywane jest wzorem: σ
1
E = ε
1
Moduł Younga moŜna przedstawić na wykresie: na którym moduł Younga definiuje się jako współczynnik kierunkowy prostoliniowego odcinka wykresu rozciągania σ = f (ε ) i równy jest co do wartości liczbowej tangesowi kąta α nachylenia liniowej części wykresu rozciągania.
Histereza powstaje, gdy obciąŜenia zmieniają się w małych granicach a odkształcenia są jeszcze spręŜyste. Zjawiska zachodzące podczas obciąŜania i odkształcania materiału moŜna wyjaśnić powstawaniem dyslokacji sieci krystalicznej materiału, które stopniowo narastają, jednakŜe przy zmianie kierunku obciąŜenia cofają się nie doprowadzając do trwałych odkształceń próbki. Potwierdza to fakt, Ŝe im wolniej odbywają się kaŜdorazowe odkształcenia próbki tym pętla histerezy spręŜystej jest węŜsza. Pole histerezy opisane pętlą histerezy jest miarą pracy zuŜytej na jednostkową objętość próbki podczas jednego cyklu obciąŜeń.
2
Umowna granica plastyczności R0,2 jest to takie napręŜenie przy jednoosiowym stanie napięcia, któremu odpowiada właściwe wydłuŜenie trwałe: F
N
R .
0 2 =
0.2
S
2
0
m
Podobnie wyznacza się R0.05
F
N
R 0.05 =
.
0 05
S
2
0
m
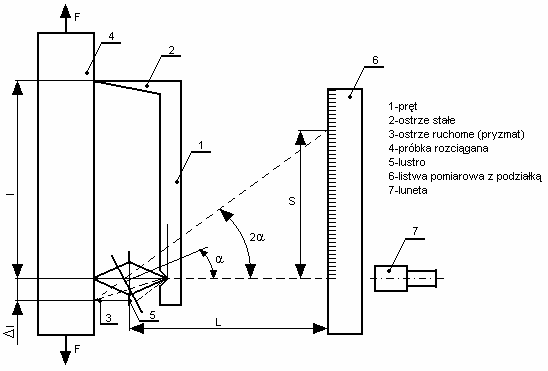
Tensometr jest przyrządem przy pomocy, którego mierzy się odkształcenia liniowe, lub napręŜenia obciąŜonej próbki, lub elementu konstrukcji. W
zaleŜności od budowy i zasady działania tensometry dzielą się na: mechaniczne, mechaniczno – optyczne, elektryczne, optyczne itp. Najczęściej dla przeprowadzenia dokładnych badań w zakresie małych odkształceń stosuje się tensometry mechaniczno – optyczne.
Rys. Schemat tensometru mechaniczno – optycznego 3
Pomiary i obliczenia Histereza spręŜystości dla: L=100[mm], d=8,5[mm], S=56,7[mm2]
WydłuŜenie
Lp
F
∆F
S
Ε
1
S2
S1+S2 ∆(S1+S2) Całkowite c
E
∆(S1+S2)10–4
[daN]
[daN] 10–1[mm] 10–1[mm]
[j]
[j]
[mm]
[mm]
105[MPa]
1
200
200
0
0
0
0
0
0
0
2
400
200
90
90
180
180
0,0180 0,0180 1,96
3
600
200
205
200
405
225
0,0405 0,0405 1,56
4
800
200
310
300
610
205
0,0610 0,0610 1,72
5 1000
200
390
390
780
170
0,0780 0,0780 2,07
6 1200
200
490
490
980
100
0,0980 0,0980 1,76
7 1400
200
600
590
1190
210
0,1190 0,1190 1,67
8 1600
200
705
700
1405
215
0,1405 0,1405 1,64
9 1800
200
820
810
1630
225
0,1630 0,1630 1,64
10 2000
200
930
920
1850
220
0,1850 0,1850 1,60
11 1800
200
860
820
1680
170
0,1680 0,1680 1,90
12 1600
200
750
745
1495
185
0,1495 0,1495 1,76
13 1400
200
650
645
1295
200
0,1295 0,1295 1,80
14 1200
200
570
530
1100
195
0,1100 0,1100 1,72
15 1000
200
465
430
895
205
0,0895 0,0895 1,72
16 800
200
365
325
690
205
0,0690 0,0690 1,64
17 600
200
260
215
475
215
0,0475 0,0475 1,64
18 400
200
150
110
260
215
0,0260 0,0260 1,64
19 200
200
25
5
30
230
0,0030 0,0030 1,53
Przykłady obliczeń
F − F
F
∆
2000 N
E
4
3
5
=
=
=
=
⋅
4
,
1 72 10
S
Ε − Ε
∆ − ∆
0 ( 4
3 )
S 0 ( 4
)
2
3
5 ,
6 7
( ,0061% − ,00405%)
MPa
mm
19
∑Ε
1
5
Ε =
=
⋅
ś
,
1 723 10 MPa
r
19
4
Wyznaczenie krzywej odkształceń całkowitych i plastycznych.
WydłuŜenie
Lp
F
∆F
S1
S2
S1+S2 ∆(S1+S2)
Ε
∆L(S
c
Εp
σ
1+S2)10–4
[daN]
[daN]
10–1[mm]
całkow. plasty.
[%]
[%]
[MPa]
1
200
0
0
0
0
0
0
0
0
2
600
400 185 185
370
370 0,0370
0,0370
105
3
1000
400 380 385
765
395 0,0765
0,0765
176
4
1400
400 590 590 1180
415 0,1180
0,1180
247
5
1800
400 800 800 1600
420 0,1600
0,1600
317
6
2200
400 1040 1000 2040
440 0,2040
0,2040
388
7
2600
400 1285 1280 2565
465 0,2565
0,2565
458
8
3000
400 1615 1610 3225
720 0,3225
0,3225
529
9
200
90
70
160
0,016
0,016 35
10 3200
2190 2185 4375 1150 0,4375
0,4375
564
11 3300
3635 3695 7330 2955 0,7330
0,7330
582
12
200
1900 1840 3740
0,374
0,374 35
Przykłady obliczeń
F
10000
3
σ =
=
=17 [
6
]
3
MPa
S
56 7
,
0
5