Układ oscylacyjny na który działa siła wymuszająca.
2
d x
m
= − kx + F ( t)
2
dt
d 2 x
2
+ ω x = F ( t) / m dt 2
0
- równanie niejednorodne
2
k
ω0 =
Podstawmy F ( t ) = F ⋅ cos(ω t ) 0
m
x = C ⋅ cos(ω t) v = − Cω ⋅ sin(ω t) 2
a = − Cω ⋅ cos(ω t) 2
− mω C ⋅ cos( t
ω )
2
= − mω ⋅ C ⋅ cos( t
ω ) + F ⋅ cos( t
ω )
0
0
x( t) = C ⋅ cos(ω t) F 0
C =
m(
2
2
ω − ω )
0
• Jeżeli ω << ω
C >
0 to
0
• Jeżeli ω >>ω to C < 0
0
• przy dużych wartościach 2
2
ω − ω amplituda maleje.
0
• Jeżeli ω ≈ ω
C →
0 to
∞ - drgania rezonansowe
1
DRGANIA WYMUSZONE z TŁUMIENIEM
d 2 x
dx
m
+ C
+ kx = F
dt 2
dt
d 2 x
dx
2
F
+
γ + ω x
0
=
dt 2
dt
m
C
gdzie γ = m
Dla harmonicznej siły wymuszającej:
F ( t ) = F ⋅ cos(ω t) 0
Rozwiązaniem równania jest:
x( t ) = x ⋅ cos( ω t + θ ) 0
F /
0
x =
m
0
([ 2ω −ω +γ ω
0
)22 2 ]122
γω
tgθ = − 2
2
ω −ω
0
2
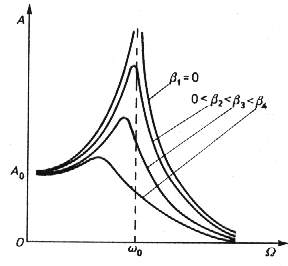
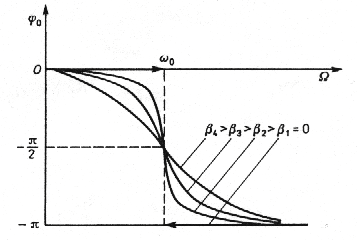
AMPLITUDA I FAZA DRGAŃ WYMUSZONYCH
F /
0
γω
x =
m
θ
0
([
tg = − 2
2
ω −ω
+ γ ω
2
ω −ω
0
0
)22 2 ]122
3
Średnia energia drgań w stanie ustalonym jest stała, równa sumie średniej energii kinetycznej i średniej energii potencjalnej.
Wartość średnia zmagazynowanej energii
< E
ω
m >= 1 m <
1
2
v > +
2
m
x
0 <
2 >
2
2
1
2
2
x = x cos ω t < x >=
x
0
0
2
1
2
2
2
v = − x ω sin ω t < v >=
x ω
0
0
2
1
< E >=
ω +ω ⋅
m
( 2 2
m
x
0 )
2
0
4
4
Żeby utrzymać stałą amplitudę drgań trzeba dostarczać energii z zewnątrz. Energia dostarczana równa jest pracy wykonywanej przez siłę zewnętrzną przeciwko sile oporu.
Moc jest równa pracy wykonanej w jednostce czasu.
Jednostką mocy jest 1 wat [1W=1 J/s]:
dW
F ⋅ ds
P =
=
= F ⋅ v
dt
dt
w przypadku ruchu jednowymiarowego, kiedy F = Fx dx
P = F dt
W ruchu drgającym moc dostarczana jest przez siłę dx
F = mγ dt
Średnia moc dostarczona:
2
dx
2
< P >=< γ ⋅ m
>=< γ ⋅ mv >
dt
1
2
2
< P >= γ ⋅ m ⋅ω x 0
2
• po włączeniu siły wymuszającej gromadzenie energii
• w stanie ustalonym pokrycie strat cieplnych.
5
2
x
+ x
γ + ω x = 0
0
~
~
iα t
rozwiązanie x = A e
Sprawdzenie:
( iα ) 2
2
x + iαγ x + ω x = 0
0
2
~
(
2
−α + iαγ + ω ) iα t
Ae
= 0
0
2
2
α − α
i γ − ω = 0
0
( równanie kwadratowe na α)
γ 1
2
2
α = i ±
− γ + 4ω0
2
2
1
1
2
2
α = γ i ± ω − γ
0
2
4
Możliwe są dwa przypadki:
2
1
2
1 2
ω − γ > 0
2
ω − γ ≤
0
0
4
lub
0
4
6
Przypadek 1
2
1 2
ω − γ > 0
0
4
Dwa rozwiązania
− 1
~
γ
ω
x
~
1 =
t
i
t
A e 2 e
γ
1
1
−
~
γ
1
t
−
2
2
i ω t
ω0 − γ =
x~
ω
4
2
= A e 2 e
γ
2
Ogólne rozwiązanie
~
−γ / 2
ˆ iω t
γ
ˆ
− ω
x = e
(
i
t
A e
+ A e γ )
1
2
Rozwiązanie rzeczywiste
γ t / 2
x =
−
A e
cos(ωγ t + ϕ )
0
0
Otrzymaliśmy oscylacje o częstości
1
2
2
1 / 2
ω = (
γ
ω − γ )
0
4
i amplitudzie
−γ t / 2
A( t ) = A e
0
A0 i ϕ0 wyznacza się z warunków początkowych 7
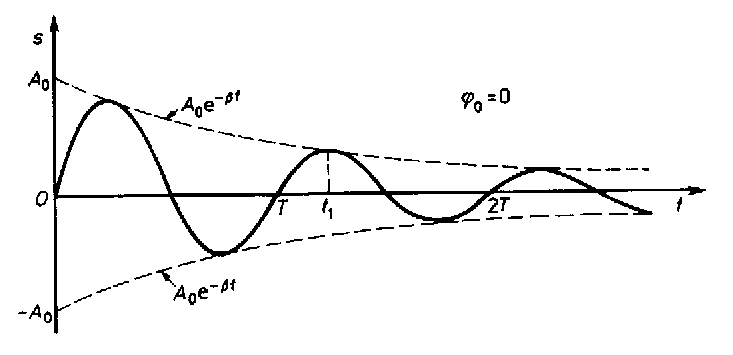
DRGANIA TŁUMIONE
γ t / 2
x =
−
A e
cos(ωγ t + ϕ )
0
0
A t
δ
( )
= ln
= /
1
(
)
2 T
γ
A t
( + T)
logartymiczny dekrement tłumienia.
8
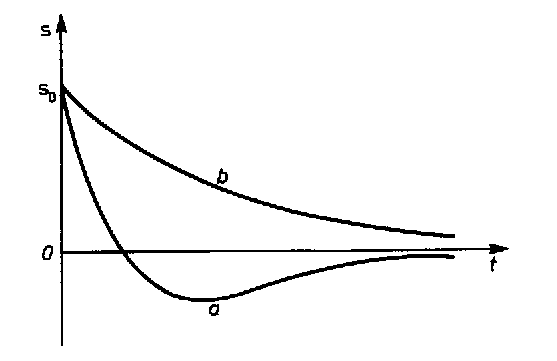
RUCH APERIODYCZNY
Przypadek 2
2
1 2
ω − γ ≤ 0
0
4
1
1
2
2
α ± = iγ ± i
γ − ω 0
2
4
jest liczbą urojoną
− a t
− a t
x = A e 1 + A e 2
1
2
gdzie a1 = ia+ oraz a2 = ia−
Rozwiązanie jest rzeczywiste i aperiodyczne.
>
typ (a) gdy v
v
α s
0 -s0 oraz
0
1
0
9
I ROZWIĄZANIE SZCZEGÓLNE
Równanie niejednorodne:
x
+ γ x
2
+ ω x = F / m
0
Rozwiązanie szczególne równania niejednorodnego: ( )
x s ( t ) = x cos( ω t + ϕ + θ ) 0
0
Jeżeli do x(s) dodamy funkcję będącą rozwiązaniem równania jednorodnego:
2
x
+ γ x + ω x = 0
0
czyli:
( o )
γ t / 2
x
t =
−
A e
ω γ t + ϕ
( )
cos(
)
0
0
lub
( o )
− a t
− a t
x
( t ) = A e 1 + A e 2
1
2
nazywaną rozwiązaniem ogólnym równania niejednorodnego, to suma tych rozwiązań też będzie rozwiązaniem równania niejednorodnego.
x( t)
( o)
= x ( t)
( s)
+ x ( t)
10