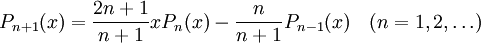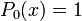Wykład 12 id 550315

Podstawy Programowania – Wykład 12

OPERATORY BITOWE

Uwaga: Operatorów tych nie moŜ na uŜ ywać do typu float lub double.

bitowa koniunkcja

bitowa alternatywa

bitowa róŜnica symetryczna ~

uzupełnienie jedynkowe

>> przesunięcie w prawo

<< przesunięcie w lewo

Koniunkcja bitowa &

Stosowana często do "zasłaniania" pewnego zbioru bitów, np.:

num & 0177;

spowoduje wyzerowanie wszystkich oprócz siedmiu najmłodszych bitów wartości zmiennej num.

Operatory przesunięcia >> oraz <<

SłuŜą do przesuwania argumentu stojącego po lewej stronie operatora o liczbę pozycji określoną przez argument stojący po prawej stronie. Np.:

num << 2;

przesuwa num w lewo o dwie pozycje, zwolnione bity wypełniane są zerami (operacja równowaŜna mnoŜeniu przez 4).

num >> 2;

dla wielkości typu unsigned zwolnione bity zawsze są wypełniane zerami. Dla wielkości ze znakiem spowoduje to wypełnienie tych miejsc bitem znaku (przesunięcie arytmetyczne), a dla wielkości bez znaku –

wypełniane zerami (przesunięcie logiczne).

W12 - 1

Podstawy Programowania – Wykład 12

#include <stdio.h> /*konwersja z kodu hex na binarny; przyklad W12P00*/

int main()

{ int j, num=0xff, bit;

unsigned int mask;

while(num!=0)

{ mask=0x80000000;

printf("Wprowadz liczbe: "); scanf("%x", &num);

printf("Rozwinieciem binarnym %08x jest: \n", num);

for(j=0; j<32; j++)

{ bit=(mask&num)?1:0; printf("%d", bit);

if(!((j+1)%4)&&(j<28)) printf("--");

mask>>=1;

}

printf("\n\n");

}

Wprowadz liczbe: abde457f

Rozwinieciem binarnym abde457f jest:

1010--1011--1101--1110--0100--0101--0111--1111

Wprowadz liczbe: 012345678

Rozwinieciem binarnym 12345678 jest:

0001--0010--0011--0100--0101--0110--0111--1000

Wprowadz liczbe: 9abcdef0

Rozwinieciem binarnym 9abcdef0 jest:

1001--1010--1011--1100--1101--1110--1111--0000

Wprowadz liczbe: 0

W12 - 2

Podstawy Programowania – Wykład 12

Bitowy operator alternatywy |

Stosowany do "ustawiania" bitów, np.:

num | mask;

ustawia 1 na tych bitach w zmiennej num, które w mask są równe 1.

Bitowa róŜnica symetryczna ^

Ustawia jedynkę na kaŜdej pozycji bitowej tam, gdzie bity w obu argumentach są róŜne, a zero tam, gdzie są

takie same.

Dopełnienie jedynkowe ~

Zamienia kaŜdy bit 1 na 0 i odwrotnie. Np.:

num & ~037;

„zasłania” zerami ostatnie 5 bitów zmiennej num (o dowolnym rozmiarze!!!). Zapis:

num & 0177740;

powoduje ten sam efekt, przy załoŜeniu, Ŝe słowo jest 16-bitowe.

/*operatory bitowe; przyklad W12P01*/

#define PRINT(f,x) printf(""#x" = %"#f"\n",(x))

#define PRINT2(f,x,y) printf(""#x"=%"#f", "#y"=%"#f"\n",(x),(y))

#include <stdio.h>

#include <limits.h>

void prbin(int);

unsigned getbits(unsigned x, int p, int n);

/*"wyciaga" n bitow ze zmiennej x od pozycji p*/

int razy10(int n);

/*mnozenie liczby calkowitej przez 10 za pomoca operatorow przesuniecia*/

W12 - 3

Podstawy Programowania – Wykład 12

int main()

{

int num=19876543210;

int i=1;

int j=23;

int mask=017777;

unsigned val;

PRINT(d,num); prbin(num);

PRINT(d,mask); prbin(mask);

PRINT(d,num & mask); /*zerowanie bitow*/

prbin(num & mask);

PRINT(d,num | mask); /*ustawianie bitow*/

prbin(num | mask);

PRINT(d,num ^ mask); /*roznica symetryczna bitow*/

prbin(num ^ mask);

PRINT(d, num << 8); /*mnozenie*/

prbin(num << 8);

PRINT(d, num >> 9); /*powielenie znaku (p.arytmet.)*/

prbin(num >> 9);

PRINT(d, ~num); /*dopelnienie jedynkowe*/

prbin(~num);

PRINT2(d,i,j);

PRINT2(d,i&j,i&&j);

printf("getbits(num,14,12) = %d\n", val=getbits(num,14,12));

prbin(val);

PRINT(d,j);

prbin(j);

PRINT(d,razy10(j));

prbin(razy10(j));

}

W12 - 4

Podstawy Programowania – Wykład 12

unsigned getbits(unsigned x, int p, int n)

{

prbin(~0<<n);

prbin(x>>(p+1-n));

return (x>>(p+1-n)) & ~(~0<<n);

}

void prbin(int znak)

{

int j;

unsigned mask=INT_MIN;

for(j=0;j<sizeof(int)*8;j++)

{

printf("%d", (mask&znak)?1:0);

if(!((j+1)%4)&&(j<sizeof(int)*7)) printf("--");

mask>>=1;

}

printf("\n");

}

int razy10(int n)

{

int m, p;

m=n<<1;

p=m<<2;

return m+p;

}

num = -1598293270

1010--0000--1011--1011--1111--1010--1110--1010

mask = 8191

0000--0000--0000--0000--0001--1111--1111--1111

W12 - 5

Podstawy Programowania – Wykład 12

num & mask = 6890

0000--0000--0000--0000--0001--1010--1110--1010

num | mask = -1598291969

1010--0000--1011--1011--1111--1111--1111--1111

num ^ mask = -1598298859

1010--0000--1011--1011--1110--0101--0001--0101

num << 8 = -1141184000

1011--1011--1111--1010--1110--1010--0000--0000

num >> 9 = -3121667

1111--1111--1101--0000--0101--1101--1111--1101

~num = -3121667

0101--1111--0100--0100--0000--0101--0001--0101

i=1, j=23

i&j=1, i&&j=1

1111--1111--1111--1111--1111--0000--0000--0000

0001--0100--0001--0111--0111--1111--0101--1101

getbits(num,14,12) = 3933

0000--0000--0000--0000--0000--1111--0101--1101

j=23

0000--0000--0000--0000--0000--0000--0001--0111

razy10(j) = 230

0000--0000--0000--0000--0000--0000--1110--0110

Operacje bitowe na znakach

Kody ASCII

Bit7

Bit6

Bit5

Bit4

Bit3

Bit2

Bit1

Bit0

0 – cyfry

0 – duŜe litery

0 – a-o

1 – litery

1 – cyfry / małe litery

1 – cyfry / p-z

W12 - 6

Podstawy Programowania – Wykład 12

#include <stdio.h> /*operacje na znakach; przyklad W12P02*/

void prbin(char znak);

char toupper(char c); /*funkcja zamienia male litery na duze*/

char tolower(char c); /*funkcja zamienia duze litery na male*/

char swapcase(char c); /*zamiana duzych liter na male i odwrotnie*/

int main()

{

char ch1='A', ch2='l', ch3='m';

prbin(ch1);

prbin(tolower(ch1));

prbin(ch2);

prbin(toupper(ch2));

prbin(ch3);

prbin(ch3=swapcase(ch3));

}

void prbin(char znak)

{

int j;

unsigned mask=0x80;

printf("znak=%c, binarnie:", znak);

for(j=0;j<sizeof(char)*8;j++)

{

printf("%d", (mask&znak)?1:0);

if(!((j+1)%4)&&(j<sizeof(char)*7))

printf("--");

mask>>=1;

}

printf("\n");

}

W12 - 7

Podstawy Programowania – Wykład 12

char toupper(char c)

{

char maska=223; /*223 – 11011111*/

return c & maska;

}

char tolower(char c)

{

return c | 32; /*32 – 00100000*/

}

char swapcase(char c)

{

return c ^ 32;

}

znak=A, binarnie:0100--0001

znak=a, binarnie:0110--0001

znak=l, binarnie:0110--1100

znak=L, binarnie:0100--1100

znak=m, binarnie:0110--1101

znak=M, binarnie:0100--1101

znak=m, binarnie:0110--1101

/*kalkulator bitowy; przyklad W12P03*/

#include <stdio.h>

#include <limits.h>

void printbin(int num);

void pline(void);

int main()

W12 - 8

Podstawy Programowania – Wykład 12

{

char op[10];

unsigned int x=0xff, y=0xff;

while(x!=0||y!=0)

{

printf("Wprowadz wyrazenie (np. abc & 789): ");

scanf("%x %s %x", &x, op, &y);

printf("\n");

switch(op[0])

{

case '&':printbin(x); printf("\t\t& (and)\n");

printbin(y); pline(); printbin(x&y);

printf("%x %c %x = %x\n\n", x, '&', y, x&y);

break;

case '|':printbin(x); printf("\t\t| (or)\n");

printbin(y); pline(); printbin(x|y);

printf("%x %c %x = %x\n\n", x, '|', y, x|y);

break;

case '^':printbin(x); printf("\t\t^ (xor)\n");

printbin(y); pline(); printbin(x^y);

printf("%x %c %x = %x\n\n", x, '^', y, x^y);

break;

case '>':printbin(x); printf("\t\t>> %d\n", y);

pline(); printbin(x>>y);

printf("%x %s %x = %x\n\n", x, ">>", y, x>>y); break;

case '<':printbin(x); printf("\t\t<< %d\n", y);

pline(); printbin(x<<y);

printf("%x %s %x = %x\n\n", x, "<<", y, x<<y); break;

W12 - 9

Podstawy Programowania – Wykład 12

case '~':printbin(x);

printf("\t\t~ (uzupelnienie)\n");

pline(); printbin(~x);

printf("%c%x = %x\n\n", '~', x, ~x);

break;

default: printf("Niepoprawny operator!\n"); break;

}

} /*koniec while*/

} /*koniec main*/

void pline(void)

{

int j;

for(j=1; j<sizeof(int)*12; j++)

printf("-");

printf("\n");

}

void printbin(int num)

{ int j, bit;

unsigned int mask;

mask=INT_MIN;

for(j=0;j<sizeof(int)*8;j++)

{

bit=(mask&num)?1:0;

printf("%d",bit);

if(!((j+1)%4)&&(j<sizeof(int)*7))

printf("--");

mask>>=1;

}

printf("\n");

}

W12 - 10

Podstawy Programowania – Wykład 12

Wprowadz wyraŜenie (np. abc & 789): abcdef97 & 45678932

1010--1011--1100--1101--1110--1111--1001--0111

& (and)

0100--0101--0110--0111--1000--1001--0011--0010

-----------------------------------------------

0000--0001--0100--0101--1000--1001--0001--0010

abcdef97 & 45678932 = 1458912

Wprowadz wyraŜenie (np. abc & 789): abcdef97 | 45678932

1010--1011--1100--1101--1110--1111--1001--0111

| (or)

0100--0101--0110--0111--1000--1001--0011--0010

-----------------------------------------------

1110--1111--1110--1111--1110--1111--1011--0111

abcdef97 | 45678932 = efefefb7

Wprowadz wyraŜenie (np. abc & 789): abcdef97 ^ 45678932

1010--1011--1100--1101--1110--1111--1001--0111

^ (xor)

0100--0101--0110--0111--1000--1001--0011--0010

-----------------------------------------------

1110--1110--1010--1010--0110--0110--1010--0101

abcdef97 ^ 45678932 = eeaa66a5

Wprowadz wyraŜenie (np. abc & 789): abcdef97 ~ 0

1010--1011--1100--1101--1110--1111--1001--0111

W12 - 11

Podstawy Programowania – Wykład 12

~ (uzupelnienie)

-----------------------------------------------

0101--0100--0011--0010--0001--0000--0110--1000

~abcdef97 = 54321068

Wprowadz wyraŜenie (np. abc & 789): abcdef97 >> 5

1010--1011--1100--1101--1110--1111--1001--0111

>> 5

-----------------------------------------------

0000--0101--0101--1110--0110--1111--0111--1100

abcdef97 >> 5 = 55e6f7c

Wprowadz wyraŜenie (np. abc & 789): abcdef97 << 5

1010--1011--1100--1101--1110--1111--1001--0111

<< 5

-----------------------------------------------

0111--1001--1011--1101--1111--0010--1110--0000

abcdef97 << 5 = 79bdf2e0

Wprowadz wyraŜenie (np. abc & 789): 0 o 0

Niepoprawny operator!

Wprowadz wyraŜenie (np. abc & 789): 0 o 0

/*szyfrowanie tekstow; przyklad W12P04*/

#include <stdio.h>

void szyfruj(char *);

void prbin(int);

W12 - 12

Podstawy Programowania – Wykład 12

int main()

{

char zdanie[50], dlug;

{

puts("wprowadz tekst do zaszyfrowania:");

gets(zdanie);

if((dlug=strlen(zdanie))!=0)

{

szyfruj(zdanie);

puts("A teraz odszyfrowanie");

szyfruj(zdanie);

}

while(dlug);

}

void szyfruj(char *zdanie)

{

char klucz[4]="4gw\n";

int i=0, z;

while((z=zdanie[i])!='\0')

{

printf("Wej=>%c=%03d=%02x->", (z>32&&z<127)?z:' ', z, z); prbin(z);

z=zdanie[i++]=z^klucz[i%4];

printf(" Wyj=%c=%03d=%02x=>", (z>32&&z<127)?z:' ', z, z); prbin(z);

printf("\n");

}

W12 - 13

Podstawy Programowania – Wykład 12

void prbin(znak)

{

int j,

int mask=0x80;

for(j=0;j<8;j++)

{

printf("%d", (mask&znak)?1:0);

if(j==3)

printf("-");

mask>>=1;

}

wprowadz tekst do zaszyfrowania:

Grodno

Wej=>G=071=47->0100-0111 Wyj=s=115=73=>0111-0011

Wej=>r=114=72->0111-0010 Wyj= =021=15=>0001-0101

Wej=>o=111=6f->0110-1111 Wyj= =024=18=>0001-1000

Wej=>d=100=64->0110-0100 Wyj=n=110=6e=>0110-1110

Wej=>n=110=6e->0110-1110 Wyj=Z=090=5a=>0101-1010

Wej=>o=111=6f->0110-1111 Wyj= =008=08=>0000-1000

A teraz odszyfrowanie

Wej=>s=115=73->0111-0011 Wyj=G=071=47=>0100-0111

Wej=> =021=15->0001-0101 Wyj=r=114=72=>0111-0010

Wej=> =024=18->0001-1000 Wyj=o=111=6f=>0110-1111

Wej=>n=110=6e->0110-1110 Wyj=d=100=64=>0110-0100

Wej=>Z=090=5a->0101-1010 Wyj=n=110=6e=>0110-1110

Wej=> =008=08->0000-1000 Wyj=o=111=6f=>0110-1111

wprowadz tekst do zaszyfrowania:

W12 - 14

Podstawy Programowania – Wykład 12

Rekurencyjny-matematyka dają cy się wyrazić za pomocą wielkoś ci uprzednio znanych; wzór rekurencyjny-

wzór pozwalają cy obliczyć wyrazy cią gu na podstawie jednego lub kilku wyrazów poprzedzają cych.

<ang. recurrent, fr. recurrent, z łac. recurrens'powracają cy'>

[Słownik Wyrazów Obcych, PWN, 1996]

Algorytm rekurencyjny w trakcie wykonywania odwołuje się do samego siebie. Aby mógł się zakończyć, jego kolejne odwołania do siebie samego muszą zaleŜeć od pewnego warunku, który zmienia się z kaŜdym kolejnym odwołaniem. Dzięki takim algorytmom, rozwiązania trudnych problemów mogą być bardzo proste.

Rekurencja oznacza wywołanie funkcji przez tę samą funkcję. Aby wyznaczyć n-tą wartość trzeba najpierw wyznaczyć wszystkie „wcześniejsze” wartości. WaŜne jest, aby kolejne wywołania funkcji rekurencyjnej były realizowane dla kolejnych wartości parametrów formalnych w taki sposób, aby nie doszło do zjawiska

„nieskończonej pętli rekurencyjnych wywołań funkcji”.

Kolejne wywołania funkcji rekurencyjnej są związane z odkładaniem na stosie programu kolejnych rekordów aktywacji funkcji. W wyniku kończenia działania poszczególnych funkcji na kolejnych poziomach rekurencji kolejne rekordy aktywacji są zdejmowane ze stosu.

Silnia - algorytm rekurencyjny:

n!=1

dla n=0 (warunek zakończenia rekurencji)

n!=n*(n-1)! dla n>0

Silnia - algorytm sekwencyjny (iteracyjny):

n!= (n-1)!*n dla n>0

/*rekurencja-silnia; przyklad W12P05*/

#include <stdio.h>

#include <stdlib.h>

long silniarek(int n); /*wersja rekurencyjna*/

long silnianrk(int n); /*wersja iteracyjna*/

W12 - 15

Podstawy Programowania – Wykład 12

int main()

{

char ciag[20];

int liczba;

long sil;

puts("REKURENCYJNE I ITERACYJNE OBLICZANIE SILNI");

{

printf("Wprowadz liczbe: ");

gets(ciag);

liczba=atoi(ciag);

if(liczba%2)

sil=silnianrk(liczba);

else

sil=silniarek(liczba);

if(sil>=0)

printf("(%d)!=%ld\n", liczba,sil);

}

while(liczba>=0);

}

long silniarek(int n)

{

int i;

printf("Adres i=%u\n", &i);

if(n>=0)

{

if(n==0 || n==1)

return (1);

else

W12 - 16

Podstawy Programowania – Wykład 12

return(n*silniarek(n-1));

}

else

printf("(%d)!=Wartosc nieokreslona\n", n);

return (-1);

}

long silnianrk(int n)

{

long s=1;

int i;

if(n>=0)

{

if(n==0 || n==1)

return (1);

else

{

for(i=2;i<=n;i++)

s*=i;

return(s);

}

else

printf("(%d)!=Wartosc nieokreslona\n", n);

return (-1);

}

REKURENCYJNE I ITERACYJNE OBLICZANIE SILNI

Wprowadz liczbe: 0

Adres i=2293508

W12 - 17

Podstawy Programowania – Wykład 12

(0)!=1

Wprowadz liczbe: 1

(1)!=1

Wprowadz liczbe: 2

Adres i=2293508

Adres i=2293476

(2)!=2

Wprowadz liczbe: 3

(3)!=6

Wprowadz liczbe: 4

Adres i=2293508

Adres i=2293476

Adres i=2293444

Adres i=2293412

(4)!=24

Wprowadz liczbe: 5

(5)!=120

Wprowadz liczbe: 6

Adres i=2293508

Adres i=2293476

Adres i=2293444

Adres i=2293412

Adres i=2293380

Adres i=2293348

(6)!=720

Wprowadz liczbe: -1

(-1)!=Wartość nieokreslona

W12 - 18

Podstawy Programowania – Wykład 12

Ciąg Fibonacciego:

F(n)=n

dla n<2

F(n)=F(n-2)+F(n-1) dla n>=2

Rekurencyjna implementacja ciągu Fibonacciego jest niezwykle nieefektywna – ma bardzo duŜą „złoŜoność

pamięciową”. Zdecydowanie bardziej efektywna jest implementacja iteracyjna.

Liczba dodawań

Liczba wywołań

Liczba przypisań

w algorytmie

algorytmu

rekurencyjnym

rekurencyjnego

iteracyjnego

177

986

1 973

10 945

21 891

121 392

242 785

1 346 268

2 692 537

/*rekurencja-Fibonacci; przyklad W12P06*/

#include <stdio.h>

#include <stdlib.h>

long fibrek(int n); /*wersja rekurencyjna*/

long fibnrk(int n); /*wersja iteracyjna*/

int main()

{

char ciag[20];

int liczba;

long fib;

puts("WYRAZY CIAGU FIBONACCIEGO (REKUR. I ITERAC.)");

{

W12 - 19

Podstawy Programowania – Wykład 12

printf("Wprowadz liczbe: ");

gets(ciag);

liczba=atoi(ciag);

if(liczba>=0)

{

if(liczba%2)

fib=fibrek(liczba);

else

fib=fibnrk(liczba);

printf("%d. wyraz ciagu Fibonacciego=%ld\n", liczba,fib);

}

else

puts("Zla wartosc - koniec obliczen");

}

while(liczba>=0);

}

long fibrek(int n)

{

int i;

printf("Adres i=%u\n",&i);

if(n<3)

return(1);

else

return(fibrek(n-1)+fibrek(n-2));

}

long fibnrk(int n)

{

long f1=1, f2=1, f=1;

int i;

for(i=3;i<=n;i++)

W12 - 20

Podstawy Programowania – Wykład 12

{

f=f1+f2;

f2=f1;

f1=f;

}

return(f);

}

WYRAZY CIAGU FIBONACCIEGO (REKUR. I ITERAC.)

Wprowadz liczbe: 0

0. wyraz ciagu Fibonacciego=1

Wprowadz liczbe: 1

Adres i=2293504

1. wyraz ciagu Fibonacciego=1

Wprowadz liczbe: 2

2. wyraz ciagu Fibonacciego=1

Wprowadz liczbe: 3

Adres i=2293504

Adres i=2293472

3. wyraz ciagu Fibonacciego=2

Wprowadz liczbe: 4

4. wyraz ciagu Fibonacciego=3

Wprowadz liczbe: 5

Adres i=2293504

Adres i=2293472

Adres i=2293440

Adres i=2293408

Adres i=2293440

W12 - 21

Podstawy Programowania – Wykład 12

Adres i=2293472

Adres i=2293440

3. wyraz ciagu Fibonacciego=2

Wprowadz liczbe: 6

6. wyraz ciagu Fibonacciego=8

Wprowadz liczbe: 7

Adres i=2293504

Adres i=2293472

Adres i=2293440

Adres i=2293408

Adres i=2293376

Adres i=2293344

Adres i=2293376

Adres i=2293408

Adres i=2293376

Adres i=2293440

Adres i=2293408

Adres i=2293376

Adres i=2293408

Adres i=2293472

Adres i=2293440

Adres i=2293408

Adres i=2293376

Adres i=2293408

Adres i=2293440

W12 - 22

Podstawy Programowania – Wykład 12

Adres i=2293408

7. wyraz ciagu Fibonacciego=13

Wprowadz liczbe: 8

8. wyraz ciagu Fibonacciego=21

Wprowadz liczbe: 28

28. wyraz ciagu Fibonacciego=317811

Wprowadz liczbe: 38

38. wyraz ciagu Fibonacciego=39088169

Wprowadz liczbe: 40

40. wyraz ciagu Fibonacciego=102334155

Wprowadz liczbe: 42

42. wyraz ciagu Fibonacciego=267914296

Wprowadz liczbe: 44

44. wyraz ciagu Fibonacciego=701408733

Wprowadz liczbe: 46

46. wyraz ciagu Fibonacciego=1836311903

Wprowadz liczbe: 48

48. wyraz ciagu Fibonacciego=512559680

Wprowadz liczbe: -1

Zla wartosc – koniec obliczen

Programy rekurencyjne są najczęściej krótkie i zwięzłe, poniewaŜ w pewnym sensie odzwierciedlają

naturalny sposób ludzkiego myślenia. Jednak mają teŜ powaŜne wady: są złoŜone obliczeniowo i wykorzystują duŜo pamięci operacyjnej.

Przy kaŜdym wywołaniu jakiejś procedury na stos trafia adres spod którego nastąpiło jej wywołanie, wszystkie parametry i zmienne lokalne. Jeśli wywołamy procedurę raz, nie ma to takiego znaczenia, ale W12 - 23

Podstawy Programowania – Wykład 12

w programach rekurencyjnych moŜe się to zdarzyć na przykład milion razy. Jeśli pamięć zarezerwowana na stos będzie niewystarczająca, na ekranie ujrzymy komunikat "Stack overflow error".

Na szczęście prawie zawsze moŜna zmienić procedurę rekurencyjną na wersję iteracyjną. W niektórych przypadkach jest to bardzo opłacalne, w innych tylko komplikuje program.

Obliczanie funkcji potęgowej xk dla x naleŜącego do zbioru liczb rzeczywistych i k naleŜącego do zbioru liczb całkowitych, zdefiniowanej w następujący sposób:

x0=1,

x1=x,

x-k=1/xk dla k>0,

xk=(xk-1)*x dla k>0 i nieparzystych,

xk=(xk/2)(xk/2) dla k>0 i parzystych

/*rekurencja-potega; przyklad W12P07*/

#include <stdio.h>

#include <stdlib.h>

double potrek(double x, int n); /*wersja rekurencyjna*/

double potnrk(double x, int n); /*wersja iteracyjna*/

int main()

{

char ciag[20];

int wyk;

double liczba, pot;

puts("REKURENCYJNA I ITERACYJNA FUNKCJA POTEGOWA");

W12 - 24

Podstawy Programowania – Wykład 12

{

printf("Wprowadz liczbe: ");

gets(ciag);

liczba=atof(ciag);

printf("Wprowadz wykladnik: ");

gets(ciag);

wyk=atoi(ciag);

if(wyk%2)

pot=potnrk(liczba,wyk);

else

pot=potrek(liczba,wyk);

if(liczba==0.0 && wyk==0)

printf("(%.2e)^(%d)=nieokreslona wartosc\n", liczba,wyk);

else

printf("(%.2e)^(%d)=%.2e\n", liczba, wyk, pot);

}

while(!(liczba==0.0&&wyk==0));

}

double potrek(double x,int n)

{

double z;

int i;

printf("Adres i=%u\n", &i);

if(n<0)

return(potrek(1.0/x,-n));

else

if(n==0)

return(1.0);

else

W12 - 25

Podstawy Programowania – Wykład 12

if(n==1)

return(x);

else

if(n%2)

return(x*potrek(x,(n-1)));

else

{

z=potrek(x,n/2);

return(z*z);

}

double potnrk(double x, int n)

{

double f=x;

int i,j=(n>0)?n:-n;

if(n==0)

return(1.0);

for(i=1;i<j;i++)

f*=x;

if(n>0)

return(f);

else

return(1.0/f);

}

REKURENCYJNA I ITERACYJNA FUNKCJA POTEGOWA

Wprowadz liczbe: 2.0

Wprowadz wykładnik: 0

Adres i=2293468

W12 - 26

Podstawy Programowania – Wykład 12

(2.00e+000)^(0)=1.00e+000

Wprowadz liczbe: 2.0

Wprowadz wykładnik: -2

Adres i=2293468

Adres i=2293420

Adres i=2293372

(2.00e+000)^(-2)=2.50e-001

Wprowadz liczbe: 8.0

Wprowadz wykładnik: -1

(8.00e+000)^(-1)=1.25e-001

Wprowadz liczbe: 3.0

Wprowadz wykładnik: 5

(3.00e+000)^(5)=2.43e+002

Wprowadz liczbe: 2.0

Wprowadz wykładnik: 6

Adres i=2293468

Adres i=2293420

Adres i=2293372

Adres i=2293324

(2.00e+000)^(6)=6.40e+001

Wprowadz liczbe: 0

Wprowadz wykładnik: 0

Adres i=2293468

(0.00e+000)^(0)=nieokreslona wartosc

Wielomiany Legendre’a mają własność ortogonalności w przedziale <-1,1> i wyraŜają się zaleŜnością

rekurencyjną:

W12 - 27

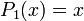
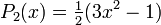
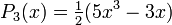
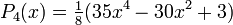
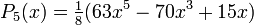
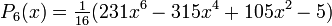
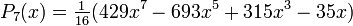
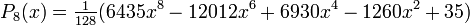
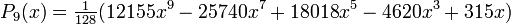
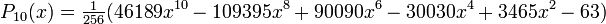
Podstawy Programowania – Wykład 12

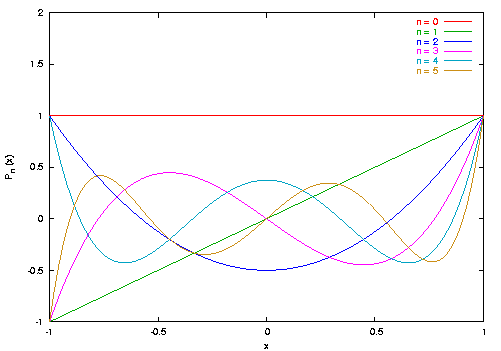
PoniŜej wymieniono kilka początkowych wielomianów Legendre'a:

W12 - 28

Podstawy Programowania – Wykład 12

/*rekurencja-wielomian Legendre'a; przyklad W12P08*/

#include <stdio.h>

#include <stdlib.h>

float legrek(float x,int n); /*wersja rekurencyjna*/

float legnrk(float x,int n); /*wersja iteracyjna*/

W12 - 29

Podstawy Programowania – Wykład 12

int main()

{

char ciag[20];

int rzad;

float leg,x;

puts("WIELOMIAN LEGENDRE'A (REKURENCJA & ITERACJA)");

{

printf("Wprowadz rzad wielomianu: ");

gets(ciag);

rzad=atoi(ciag);

if(rzad>=0)

{

printf("Wprowadz zmienna x: ");

gets(ciag);

x=atof(ciag);

if(rzad%2)

leg=legrek(x,rzad);

else

leg=legnrk(x,rzad);

printf("Legendre%d(%.2e)=%.2e\n", rzad, x, leg);

}

while(rzad!=-10);

}

float legrek(float x,int n)

{

int i;

printf("Adres i=%u\n", &i);

W12 - 30

Podstawy Programowania – Wykład 12

if(n==0)

return(1.0);

else

if(n==1)

return(x);

else

return(((2*n-1)*x*legrek(x,n-1)-(n-1)*legrek(x,n-2))/n);

}

float legnrk(float x,int n)

{

float p0, p1=1, p2=x;

int i;

if(n==0)

return(1.0);

else

if(n==1)

return(x);

else

{

for(i=2;i<=n;i++)

{

p0=p1;

p1=p2;

p2=((2*i-1)*x*p1-(i-1)*p0)/i;

}

return(p2);

}

W12 - 31

Podstawy Programowania – Wykład 12

WIELOMIAN LEGENDRE’A (REKURENCJA & ITERACJA)

Wprowadz rzad wielomianu: 2

Wprowadz zmienna x: 1

Adres i=2293492

Adres i=2293460

Legendre2(1.00e+000)=1.00e+000

Wprowadz rzad wielomianu: 3

Wprowadz zmienna x: 2

Legendre3(2.00e+000)=1.70e+001

Wprowadz rzad wielomianu: 4

Wprowadz zmienna x: -0.5

Adres i=2293492

Adres i=2293460

Adres i=2293428

Adres i=2293396

Adres i=2293428

Adres i=2293460

Adres i=2293428

Legendre4(-5.00e-001)=-2.89e-001

Wprowadz rzad wielomianu: 5

Wprowadz zmienna x: 2

Legendre5(2.00e+000)=1.86e+002

Wprowadz rzad wielomianu: -10

W12 - 32

Podstawy Programowania – Wykład 12

Funkcja Ackermanna została odkryta przez Wilhelma Ackermanna w 1928 roku. Cechą charakterystyczną tej dwuargumentowej funkcji matematycznej, będącej prostym przykładem funkcji rekurencyjnej (co moŜna udowodnić!), jest jej nadzwyczaj szybki wzrost.

Funkcja Ackermanna nadaje się do testowania zdolności kompilatorów do optymalizacji kodu wynikowego.

W jej przypadku dobra optymalizacja moŜe oznaczać skrócenie czasu wykonywania programu o trzy lub cztery rzędy wielkości.

Matematyczna definicja funkcji opisana jest wzorem (m,n – liczby naturalne):

A(m,n)=A(m-1,A(m,n-1))

dla m>0 i n>0

A(0,n)=n+1

dla n>0

A(m,0)=A(m-1,1)

dla m>0

Tab. Wartości funkcji Ackermanna

m\ n

n + 1

2 + (n + 3) − 3

2 * (n + 3) − 3

125

2(n + 3) − 3

65533

265536−3

A(3,265536 −3)

A(3,A(4, 3))

b. duŜa licz.

65533

A(4,65533)

A(4,A(5,1))

A(4,A(5,2))

A(4,A(5,3))

b. duŜa licz.

A(5,1)

A(5,A(5,1))

A(5,A(6,1))

A(5,A(6,2))

A(5,A(6,3))

b. duŜa licz.

Wartość A(4,2) (>10^10^1019000) jest (podobno!) wię ksza niŜ liczba czą steczek we wszechś wiecie

podniesiona do dwusetnej potę gi.

W12 - 33

Podstawy Programowania – Wykład 12

Trudności w obliczeniu wartości funkcji Ackermanna powodowane są głównie złoŜonością wywołań

rekurencyjnych, które łatwo mogą doprowadzić do przepełnienia stosu. Podczas wykonywania obliczenia dochodzi wielokrotnie do wywołań funkcji z identycznymi argumentami (patrz na poniŜsze przykłady).

Odpowiednia implementacja funkcji moŜe wykorzystać powtarzające się instrukcje do znacznego skrócenia procesu obliczania. Przykładowo wartość a(2,0)=3, a a(1,2)=4 co daje się odczytać z tabelki. Poza tym, np. a(2,1)=a(1,3)=a(0,4). RóŜnica polega na tym, Ŝe ostatnia kombinacja argumentów moŜe zostać

obliczona w czasie krótszym (1 wywołanie funkcji) niŜ druga (8 wywołań funkcji) lub pierwsza (14 wywołań).

/*rekurencja-funkcja Ackermanna; przyklad W12P09*/

#include <stdio.h>

#include <stdlib.h>

int acker(int m, int n);

int main()

{

int p1,p2,a;

char ciag[20];

puts("REKURENCYJNA FUNKCJA ACKERMANNA");

{

printf("Wprowadz m: ");

gets(ciag);

p1=atoi(ciag);

printf("Wprowadz n: ");

gets(ciag);

p2=atoi(ciag);

a=acker(p1,p2);

if(a==-1)

printf("ackermann(%d,%d)<=niepoprawne parametry\n", p1, p2);

W12 - 34

Podstawy Programowania – Wykład 12

else

printf("ackermann(%d,%d)=%d\n", p1, p2, a);

}

while(p1!=-10);

}

int acker(int m, int n)

{

int a;

printf("**wywolanie acker(%d,%d)\n", m, n);

if((m<0)||(n<0))

a=-1;

else

if(m==0)

a=n+1;

else

if(n==0)

a=acker(m-1,1);

else

a=acker(m-1,acker(m,n-1));

printf("--powrot z acker(%d,%d)=%d\n", m, n, a);

return(a);

}

REKURENCYJNA FUNKCJA ACKERMANNA

Wprowadz m: -3

Wprowadz n: 3

**wywolanie acker(-3,3)

--powrot z acker(-3,3)=-1

ackermann(-3,3)<=niepoprawne parametry

W12 - 35

Podstawy Programowania – Wykład 12

Wprowadz m: 0

Wprowadz n: 8

**wywolanie acker(0,8)

--powrot z acker(0,8)=9

ackermann(0,8)=9

Wprowadz m: 1

Wprowadz n: 2

**wywolanie acker(1,2)

**wywolanie acker(1,1)

**wywolanie acker(1,0)

**wywolanie acker(0,1)

--powrot z acker(0,1)=2

--powrot z acker(1,0)=2

**wywolanie acker(0,2)

--powrot z acker(0,2)=3

--powrot z acker(1,0)=3

**wywolanie acker(0,3)

--powrot z acker(0,3)=4

--powrot z acker(1,2)=4

ackermann(1,2)=4

Wprowadz m: -10

Wprowadz n: 0

**wywolanie acker(-10,0)

--powrot z acker(-10,0)=-1

ackermann(-10,0)<=niepoprawne parametry

W12 - 36

Podstawy Programowania – Wykład 12

Legenda, napisana przez Eduarda Lucas - francuskiego matematyka (1842-1891), który w roku 1883 wymyś lił

grę zwaną WieŜ e Hanoi: "W Indiach, w mieś cie Banares, pod kopułą głównej ś wią tyni, w miejscu, gdzie

znajduje się ś rodek Ziemi, postawił Brahma na brą zowej tabliczce trzy diamentowe pałeczki o wysokoś ci

jednego łokcia i o gruboś ci tułowia pszczoły. Przy stworzeniu ś wiata na jedną z tych pałeczek nanizane

zostały 64 krąŜ ki z czystego złota z otworami poś rodku tak, iŜ utworzyły postać ś cię tego stoŜ ka. Kapłani

luzują c się wzajemnie dniem i nocą bez przystanku, zaję ci są przeniesieniem tego stoŜ ka z pierwszej pałeczki

na trzecią , posiłkują c się przejś ciowo pałeczką drugą , przy czym zobowią zani są najsurowiej przestrzegać

dwu nastę pują cych zakazów: po pierwsze, za jednym uję ciem nie przenosić nigdy wię cej ponad jeden

krąŜ ek; po wtóre, nigdy nie kłaść krąŜ ka wię kszego na mniejszym. Gdy kapłani, zachowują c ś ciś le te

przepisy, ukoń czą swą pracę , nastą pi koniec ś wiata..."

Szczepan Jeleń ski - Lilavati, Rozrywki

/*rekurencja-wieŜe Hanoi; przyklad W12P10*/

#include <stdio.h>

#include <stdlib.h>

void hanoi(int n, int skad, int dokad, int przez);

int main()

{

int lk;

char ciag[10];

puts("WIEZE HANOI - WERSJA REKURENCYJNA");

{

printf("Wprowadz liczbe krazkow: ");

gets(ciag);

lk=atoi(ciag);

if(lk>0)

hanoi(lk,1,3,2);

W12 - 37

Podstawy Programowania – Wykład 12

}

while(lk!=-10);

}

void hanoi(int n, int skad, int dokad, int przez)

{

if(n>0)

{

hanoi(n-1,skad,przez,dokad);

printf("przesunac jeden krazek z %d na %d\n", skad, dokad);

hanoi(n-1,przez,dokad,skad);

}

WIEZE HANOI – WERSJA REKURENCYJNA

Wprowadz liczbe krąŜków: -3

Wprowadz liczbe krąŜków: 0

Wprowadz liczbe krąŜków: 1

przesunac jeden krazek z 1 na 3

Wprowadz liczbe krąŜków: 2

przesunac jeden krazek z 1 na 2

przesunac jeden krazek z 1 na 3

przesunac jeden krazek z 2 na 3

Wprowadz liczbe krąŜków: 3

przesunac jeden krazek z 1 na 3

przesunac jeden krazek z 1 na 2

przesunac jeden krazek z 3 na 2

przesunac jeden krazek z 1 na 3

przesunac jeden krazek z 2 na 1

przesunac jeden krazek z 2 na 3

przesunac jeden krazek z 1 na 3

W12 - 38

Podstawy Programowania – Wykład 12

Wprowadz liczbe krąŜków: 4

przesunac jeden krazek z 1 na 2

przesunac jeden krazek z 1 na 3

przesunac jeden krazek z 2 na 3

przesunac jeden krazek z 1 na 2

przesunac jeden krazek z 3 na 1

przesunac jeden krazek z 3 na 2

przesunac jeden krazek z 1 na 2

przesunac jeden krazek z 1 na 3

przesunac jeden krazek z 2 na 3

przesunac jeden krazek z 2 na 1

przesunac jeden krazek z 3 na 1

przesunac jeden krazek z 2 na 3

przesunac jeden krazek z 1 na 2

przesunac jeden krazek z 1 na 3

przesunac jeden krazek z 2 na 3

Wprowadz liczbe krąŜków: -10

/*wieze Hanoi-wersja iteracyjna;przyklad W12P11*/

#include <stdio.h>

#include <stdlib.h>

int a[10][4], gora[4];

void hanoi(int n);

void przenies(int z, int na);

int main()

{

int lk;

char ciag[10];

W12 - 39

Podstawy Programowania – Wykład 12

do {

printf("Wprowadz liczbe krazkow: ");

gets(ciag);

lk=atoi(ciag);

if(lk>0)

hanoi(lk);

}

while(lk!=-10);

}

void przenies(int z, int na)

{

printf("Przenies %d z %d na %d\n", a[gora[z]][z], z, na);

gora[na]=gora[na]+1;

a[gora[na]][na]=a[gora[z]][z];

gora[z]=gora[z]-1;

}

void hanoi(int n)

{

int i,j,k,maly;

for(i=n; i>=1; i--)

a[n-i+1][1]=i;

gora[1]=n;

for(i=1;i<=3;i++)

a[0][i]=n+1;

gora[2]=0;

gora[3]=0;

maly=1;

W12 - 40

Podstawy Programowania – Wykład 12

{

i=maly+1;

if(i>3) i=i-3;

przenies(maly,i);

maly=i;

if(gora[i]!=n)

{

j=i+1;

if(j>3) j=j-3;

k=i+2;

if(k>3) k=k-3;

if(a[gora[j]][j]<a[gora[k]][k]) przenies(j,k);

else przenies(k,j);

}

while(!((gora[1]==n)||(gora[2]==n)||(gora[3]==n)));

}

Referencje

http://binboy.sphere.pl/index.php?show=140

http://www.ia.pw.edu.pl/~stachurs/w3.pdf

http://projekty.pc.pl/materialy/ajd/wi/wiw06.pdf

http://www.neurosoft.edu.pl/jbartman/AiSD_w3_Rekurencja.pdf

http://wipos.p.lodz.pl/zylla/games/hanoi-expl.html

http://chemeng.p.lodz.pl/zylla/games/hanoi5p.html

http://wipos.p.lodz.pl/zylla/games/hanoi-iter1.html

http://pl.wikipedia.org/wiki/Wielomiany_Legendre'a

http://pl.wikipedia.org/wiki/Funkcja_Ackermanna

W12 - 41