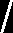
Mechanika – Rysowanie wykresów momentów gnących i sił tnących Algorytm rozwiązania zadnia:

1. Wyznaczenie wartości reakcji w podporach – układ płaski dowolny a więc trzy równania:

∑ = 0

∑ = 0

∑ = 0

lub ∑ = 0

∑ = 0

∑ = 0

Znaki momentów określamy zgodnie z zasadą wskazówek zegara czyli: Obciążenie ciągłe zamieniamy na siłę wypadkową Q=q*L gdzie L= długość odcinka belki, na którym działa obciążenie ciągłe.

2. Podział belki na przedziały (granice przedziałów ustalamy w miejscu przyłożenia siły, momentu lub reakcji a także na początku i na końcu obciążenia ciągłego).

3. Dla każdego przedziału układamy równanie momentów (względem miejsca odcięcia).

Znaki momentów określamy zgodnie z zasadą „wyginania belki” czyli: x

x

Wypadkową z obciążenia ciągłego wyznaczamy z przedziału o długości X (NIE Z CAŁOŚCI): Q=q*x

Mg=-Q*0.5x=-0.5*q*x2

Q

Strona 1

Opracował mgr inż. Łukasz Doliński

grudzień 2011

PDF created with pdfFactory Pro trial version www.pdffactory.com

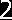
Mechanika – Rysowanie wykresów momentów gnących i sił tnących Dla obciążenia ciągłego wyznaczamy współrzędną wierzchołka paraboli xw. Jeżeli xw mieści w granicach przedziału to obliczamy wartość momentu dla wierzchołka paraboli Mg(xw). Jeżeli xw nie mieści się w granicach danego przedziału to łączymy otrzymane punkty na granicach przedziału kawałkiem paraboli.

Uwaga.

Jedynie w miejscu przyłożenia momentu M na wykresie momentów gnących może być skok wartości (na granicy przedziałów wartość momentu gnącego jest różna z lewej strony i z prawej). W każdym innym przypadku wartości z lewej i prawej strony granicy przedziału muszą być jednakowe.

Przykład

Dane:

q=1kN/m

M=1kNm

q

P= 1kN

A

B

M

P

L= 1m

1. Uwolnienie od więzów i obliczenie

reakcji w podporach A i B.

= 0 → = 0

= 0 → + − + = 0

A

B

Q

M

P

Ponieważ RBX = 0 to w dalszych obliczeniach

RBY będzie oznaczane jako RB

= 0 → − ∙ − ∙ − + ∙ 4

= 0

lub

= 0 → − ∙ 5 − ∙ 4 + ∙ 3 −

= 0

Gdzie Q=q*2l

Po rozwiązaniu układu równań

RA = 0

RB = 1

Strona 2

Opracował mgr inż. Łukasz Doliński

grudzień 2011

PDF created with pdfFactory Pro trial version www.pdffactory.com

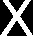
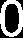
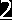
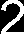
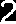
Mechanika – Rysowanie wykresów momentów gnących i sił tnących 2. Podział belki na przedziały

Przedział 1, 2 i 3 będą liczone od lewej strony, a przedział 4 od prawej strony.

q

M

1

2

3 4

P

3. Równanie momentów dla pierwszego

przedziału:

q

= ∙ /

Mg1(0)=0

P

M

Mg1(l)=Pl=1

4. Równanie momentów dla drugiego

przedziału:

= ∙ ( + )+ ∙ −

2 /

qdzie Q2=qx2, a więc

Q

P

2

M

= ∙ ( + )+ ∙ − 2 /

1.5

Mg2(0)=1

1

Mg2(l) =1

0

l

Wierzchołek paraboli:

( ) ′ = + − ∙ = 0

= = 1

Wierzchołek paraboli znajduje się we

współrzędnej x2=1 i ma wartość:

Mg2(1) =1,5

Strona 3

Opracował mgr inż. Łukasz Doliński

grudzień 2011

PDF created with pdfFactory Pro trial version www.pdffactory.com

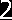
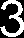
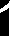
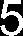
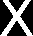
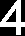
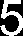
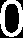
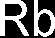
Mechanika – Rysowanie wykresów momentów gnących i sił tnących 5. Równanie momentów dla trzeciego przedziału:

= ∙ ( + 3 )+ ∙ ( + 2 ) − ∙ ( + ) /

gdzie Q =q*2l

P

Q

M

= ∙ ( + 3 )+ ∙ ( + 2 ) − ∙ 2 ∙ ( + ) /

Mg3(0)=1

Mg3(l) =0

6. Równanie momentów dla czwartego

przedziału (od prawej strony):

= ∙ /

Mg4(0)=0

Mg4(l) =1

P

M

7. Rysowanie wykresu sił tnących

(pochodne momentów gnących dla

odpowiednich przedziałów):

= ( ) ′ = = 1

= ( ) ′ = + − ∙ /

(0) = 1 ; (2 ) = −1

= ( ) ′ = + − ∙ 2 = −1

= −( ) ′ = − = −1

(w czwartym przedziale zmieniamy znak

na przeciwny ponieważ liczymy go od

prawej do lewej)

Strona 4

Opracował mgr inż. Łukasz Doliński

grudzień 2011

PDF created with pdfFactory Pro trial version www.pdffactory.com