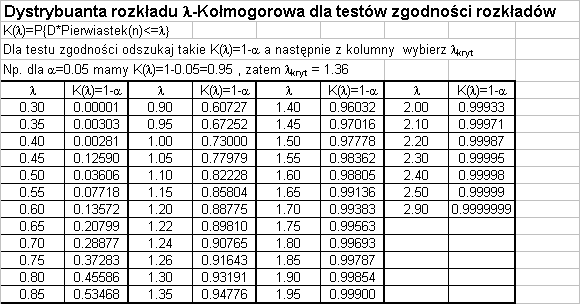
Test stosowany do sprawdzenia zgodności rozkładu empirycznego z rozkładem hipotetycznym. Warunkiem zastosowania jest to aby hipotetyczna dystrybuanta była ciągła a próba losowa liczna ( duże n).
Hipoteza zerowa H : F(x)=F (x) - rozkład empiryczny jest zgodny z 0
0
ciągłym rozkładem hipotetycznym o dystrybuancie określonej funkcją F (x)
0
Hipoteza alternatywna: H : F(x)≠F (x)
0
0
Statystyka testowa : λ = D n
;
D = sup F ( x) − F ( x) n
0
x
Przy założeniu prawdziwości H statystyka λ ma asymptotyczny rozkład 0
λ-Kołmogorowa , gdzie n –liczebność próby rozkładu empirycznego, i
F ( x) – dystrybuanta empiryczna ( z def. F ( x) ns
= ∑
dla
x ≤ x ≤ x
n
n
i
i 1
+
)
n
s 1
=
Odrzucenie hipotezy zerowej, gdy stat. λ ∈Ω {λ : P[λ ≥ λ
(α)]= α}
kryt
Rozkład λ-Kołmogorowa
1.0
0.9
0.8
Dystrybuanta
0.7
rozkładu
0.6
0.5
0.4
λ-Kołmogo-
0.3
rowa
0.2
0.1
0.0
0.00
0.50
1.00
1.50
2.00
2.50
3.00
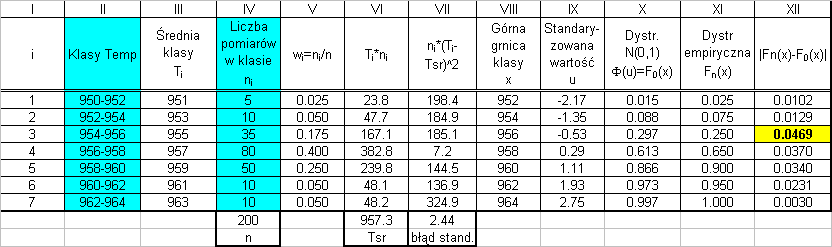
Przykład. Zakłada się że sonda pomiarowa temperatury podaje wyniki pomiarów o rozkładzie normalnym, gdy pomiary są powtarzane wielokrotnie, dla tych samych warunków eksperymentu. Za pomocą sondy wykonano 200 pomiarów temperatury, otrzymując rozkład empiryczny w Tabeli 1 (II,IV –kolumny). Zweryfikuj postawioną hipotezę, o normalności rozkładu temperatury, w oparciu o uzyskane wyniki.
Uwagi do tablicy: Parametry hipotetycznego rozkładu normalnego są szacowane na podstawie próbki. Dystrybuanta hipotetycznego rozkładu N(0,1) wyznaczana na podstawie tablic dystrybuanty Φ(u) standaryzowanego rozkładu normalnego.
Wniosek: Wyznaczona wartość D=0.0469 , pozwala na obliczenie statystyki testu λ=D√n=0.663 . Przyjąwszy poziom istotności α=0.05 , z tablic rozkładu Kołmogorowa pobieramy wartość krytyczną λ
= 1.36. Wobec faktu,
= 1.36 , nie
kryt
że λ=0.663 < λkryt
ma podstaw do odrzucenia hipotezy zerowej H ,
0
że rozkład jest normalny, ze średnią
957.3 i błędem standardowym σ=2.44 .
Test stosowany do sprawdzenia zgodności rozkładu empirycznego z rozkładem
hipotetycznym.
Warunkiem
zastosowania
jest
odpowiednio duża próba losowa ( n liczebność próby).
Hipoteza zerowa H : F(x)=F (x) - rozkład empiryczny jest zgodny z 0
0
rozkładem hipotetycznym o dystrybuancie określonej funkcją F (x) 0
Hipoteza alternatywna: H : F(x)≠F (x)
0
0
k
( n − np
i
i )2
Statystyka testowa : Z = ∑
i=
( npi )2
1
Przy założeniu prawdziwości H statystyka Z ma asymptotyczny 0
rozkład χ2 o r = ( k– m–1) stopniach swobody, gdzie k –liczba klas wartości zmiennej empirycznej, m – liczba parametrów rozkładu F (x), p – prawdopodobie
0
i
ństwo przyjęcia przez zmienna losową
wartości z przedziału dla klasy i (obliczać można ze znanej dystrybuanty F (x) ). Symbol n oznacza liczebno 0
i
ść w klasie i.
Odrzucenie hipotezy zerowej, gdy stat. Z ∈Ω [z: P{z≥χ2(α,r)}= α]
Test zgodności χ2 – cd.
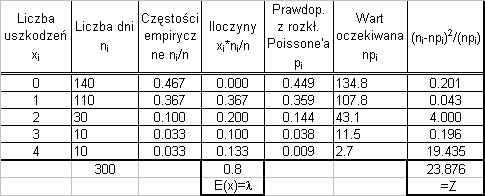
Przykład. Przez rok rejestrowano liczbę awarii urządzenia, zapisując liczbę uszkodzeń w ciągu jednego dnia roboczego. Otrzymano empiryczny rozkład (Tabela). Zweryfikować hipotezę, iż rozkład jest zgodny z rozkładem Poissone’a.
Na początek z próbki empirycznej szacujemy parametr λ rozkładu Poissone’a ( λ =
średnia wartość z próby empirycznej ). Zmienna X jest skokowa, zatem k
λ
P( X = k ) =
e−λ
k = 0 1
, , 2, 3, 4
k !
Tabela 1
UWAGI: p dla X=4 wyznaczone
i
jako 1–(p +p +p +p ) aby Σp =1.
0
1
2
3
i
Ponieważ wartość oczekiwana dla
X=4 wynosi 2.7 < 5 , dokonujemy
połączenia danych z sąsiednich klas,
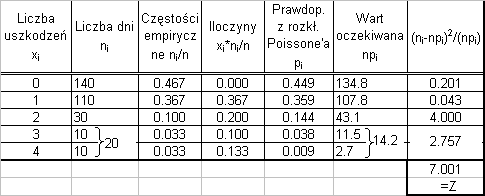
stąd ostatecznie powstaje Tabela 2.
Tabela 2
Wniosek:
Ponieważ
statystyka
testowa Z=7.001 > χ2(0.05,2)=5.991
odrzucamy hipotezę H – oznacza to
0
że rozkład empiryczny istonie różni
się od rozkładu Poissone’a. Liczba
stopni swobody = k–m–1= 4–1–1= 2



Jak to zrobić w STATISTICA
Program
domyślnie
wykonuje
test
Chi-kwadrat
na
podstawie
liczności
obserwowanych i oczekiwanych. Kategorie, w obrębie których liczności oczekiwane są niższe od 5, są łączone tak, aby utworzyły klasy o wyższej liczności. Jeżeli test wykazuje istotność (tzn. wartość p jest mniejsza od założonego poziomu istotności, zazwyczaj równego 0,05 lub 0,01), wówczas odrzucamy
hipotezę
zakładającą,
że
obserwowane
dane
podlegają
określonemu rozkładowi.
α > α
1
2 - małe typowo 0.05, 0.01
α =P( χ
1
> χ2(α ,k) )
1
α = P( χ
2
> χ2(α ,k) )
2
χ2(α ,k)
χ2(α ,k)
1
2
χ
Jeśli statystyka χ z próby jest:
χ> χ2(α ,k) – odrzu
( prawdopodobie
)
1
ć H0
ństwo otrzymania χ wynosi mniej niż α1
= ISTOTNOŚĆ testu
Odległość emp. rozkładu od teoretycznego tak duża, że szansa na to jest mniejsza α1