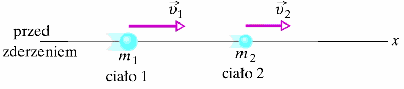
Zderzenie sprężyste centralne (w jednym wymiarze)
zasada zachowania pędu:
'
'
m υ + m υ = m υ + m υ
1 1
2
2
1 1
2
2
(1)
= ppocz
= pkońc
zasada zachowania energii mechanicznej (w tym przypadku wyłącznie energia kinetyczna) 1
2
1
2
1
2
1
2
'
'
m υ
+ m υ = m υ + m υ
1 1
2
2
1 1
2
2
/ ⋅ 2
(2)
2
2
2
2
= εk( pocz)
= εk( końc)
równania (1) i (2) należy rozwiązać razem jako układ równań równanie (2) jest równaniem kwadratowym – rozwiązanie utrudnione można uzyskać dwa niezależne równania liniowe porządkujemy równania (1) i (2) ze względu na masy m 1 i m 2: m (
'
υ − υ )
= − m (
'
υ − υ )
1
1
1
2
2
2
(3)
2
2
2
2
m (
'
υ − υ ) = − m (
'
υ − υ )
1
1
1
2
2
2
(4)
(
'
υ − υ )(
'
υ + υ )
= (
'
υ − υ )(
'
υ + υ
=
)
1
1
1
1
2
2
2
2
dzielimy (4) przez (3):
'
'
υ + υ = υ + υ
1
1
2
2
(5)
równania (3) i (5) rozwiązujemy jako układ równań: m (
'
υ − υ ) = − m (
'
υ − υ )
1
1
1
2
2
2
(3)
'
'
υ + υ = υ + υ
1
1
2
2
(5)
'
np. z (5) wyznaczamy υ 2
υ' = υ + υ' − υ
2
1
1
2
i podstawiamy do (3), mnożąc wszystkie nawiasy: m υ − m υ' = − m υ + m υ + m υ' − m υ
1 1
1 1
2
2
2 1
2 1
2
2
'
( m − m ) υ + m
2
υ = ( m + m ) υ
1
2
1
2
2
1
2
1
2 m
'
1
2
2
υ =
υ +
υ
1
1
2
m + m
m + m
(6)
1
2
1
2
podstawiając '
υ
υ
1 (5) obliczamy
'
2
m − m
2 m
m + m + m − m
2 m − m − m
'
1
2
2
1
2
1
2
2
1
2
υ = υ +
υ +
υ − υ =
υ +
υ
2
1
1
2
2
1
2
m + m
m + m
m + m
m + m
1
2
1
2
1
2
1
2
2 m
m − m
'
1
2
1
υ =
υ +
υ
2
1
2
m + m
m + m
(7)
1
2
1
2
równania (6) i (7) są symetryczne
w przypadku kiedy ciało 2 porusza się przed zderzeniem w lewo, należy podstawić wartość υ
υ
υ
2 < 0; wartości
'
1 < 0 lub
'
2 < 0 otrzymane w tym przypadku należy również interpretować jako ruch odpowiedniego ciała w lewo po zderzeniu