Politechnika Warszawska
Wydział Inżynierii lądowej Instytut Mechaniki Konstrukcji Inżynierskich Zakład Wytzrymałości Materiałów Teorii Sprężystości i Plastyczności Praca projektowa
Wykonał Piotr Skorek
Zadanie 1
Dane do zadania:
kN := 1000⋅N
4
kN
kN
kN
E := 2.05⋅
kN
10 ⋅
R
:=
⋅
:=
⋅
:=
⋅
H
19
Re
23
R
20.5
2
2
2
2
cm
cm
cm
cm
λ := π
E
gr
RH
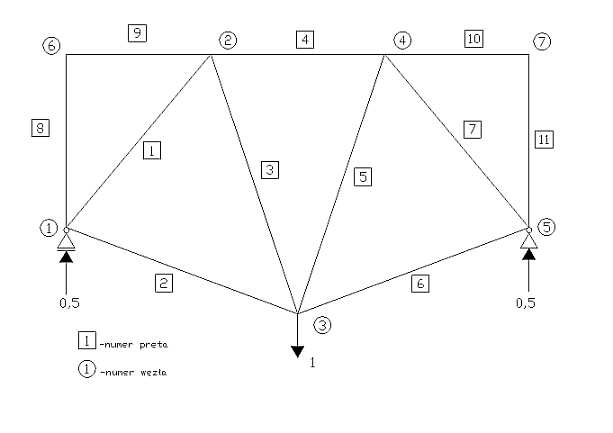
Geometria kratownicy
2
2
L :=
(
⋅
+ (
⋅
=
:=
:=
1
250 cm)
300 cm) L1 390.512 cm cosβ
250cm
sinβ
300cm
L1
L1
2
2
L :=
(
⋅ ) + (150⋅cm) L =
cosα
400cm
:=
sinα
150cm
:=
2
400 cm
2
427.2 cm
L
L
2
2
2
2
L :=
(
⋅
+ (
⋅
=
3
450 cm)
150 cm) L3 474.342 cm
cosγ
450cm
:=
sinγ
150cm
:=
L
L :=
⋅
3
L3
4
300 cm
L :=
5
L3
L :=
=
=
6
L2
cosα
0.936
sinα
0.351
L :=
7
L1
L :=
=
=
8
300cm
cosβ
0.64
sinβ
0.768
L
:=
11
L8
cosγ = 0.949
sinγ = 0.316
L :=
9
250cm
L
:=
10
L9
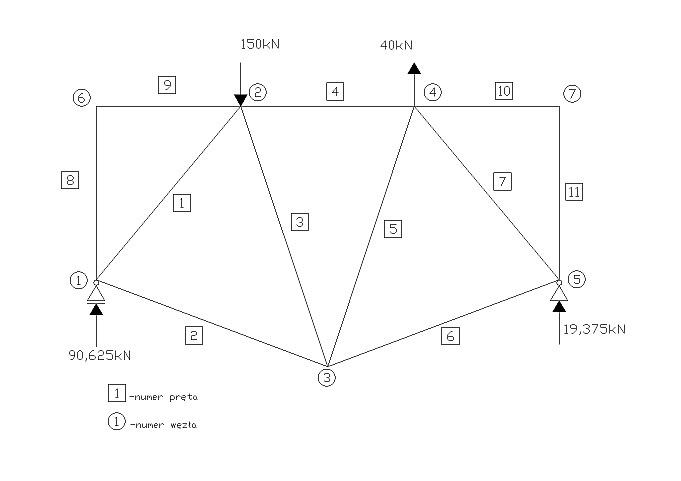
Obliczenie reakcji
150kN⋅550cm − 40kN⋅250cm
S :=
:=
R :=
S
R =
8
0
10
0
1
1
90.625 kN
800cm
S :=
S
:=
150⋅kN⋅250cm − 40kN⋅550cm
9
0
11
0
V :=
V =
5
5
19.375 kN
800cm
H := ⋅
5
0 kN
Obliczenie sił podłużnych w kratownicy Węzeł 1
R −
⋅
+
⋅
1
S2 sinα S1 sinβ = 0
S ⋅
+
⋅
2 cosα
S1 cosβ = 0
S = −
1
89.88 kN
S =
2
61.452 kN


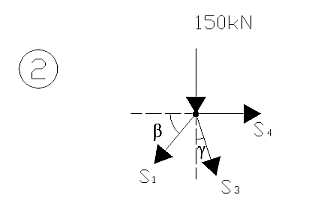
Węzeł 2
S
− ⋅
−
−
⋅
1 sinβ
150kN
S3 cosγ = 0
S +
⋅
−
⋅
4
S3 sinγ S1 cosβ = 0
S = −
3
85.331 kN
S = −
4
30.556 kN
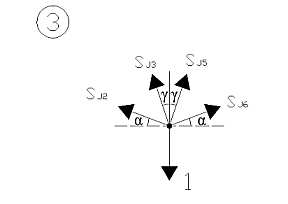
Węzeł 5
S ⋅
+
⋅
6 cosα
S7 cosβ = 0
V −
⋅
+
⋅
5
S6 sinα S7 sinβ = 0
S =
6
13.138 kN
S = −
7
19.216 kN
Węzeł 4
40kN − S ⋅
−
⋅
7 sinβ
S5 cosγ = 0
S
−
−
⋅
+
⋅
4
S5 sinγ S7 cosβ = 0
S = −
4
30.556 kN
S =
5
57.724 kN
Węzeł 3 - spr
S ⋅
+
⋅
+
⋅
+
⋅
=
2 sinα
S3 cosγ S5 cosγ S6 sinα 0 N
OK!
1.W prętach rozciąganych pasa dolnego (2, 6) P
:=
max
S2
P
=
max
61.452 kN
Pmax
2
A :=
=
1
A1 2.998cm
R
Przyjęto przekrój ][40:
2
A :=
⋅
1
7.02 cm
4
4
I
:=
⋅
:=
⋅
y1
14.52 cm
Iz1
11.40 cm
i
:=
⋅
:=
⋅
y1
1.44 cm
iz
1.27 cm
2.W prętach ściskanych pasa górnego (4) L =
:=
4
300 cm
Pmax
S4
P
= −
λ =
kN
max
30.556 kN
gr
103.193
R = 20.5
2
cm
Dla przekroju ][40
2
i
:=
⋅
:=
⋅
min
1.27 cm
A2
7.02 cm
L
λ
4
:=
λ = 236.22
imin
π2⋅E
kN
R
:=
=
kr
Rkr 3.626
λ2
2
cm
P
:=
⋅
=
kr
Rkr A2
Pkr 25.454 kN
3.W pozostałych prętach
3.1 rozciąganych (5)
P
:=
max
S5
P
=
max
57.724 kN
Pmax
2
A
:=
=
3r
A3r 2.816cm
R
3.2 ściskanych (1,3, 7)
pręt 1 i 3
kN
L =
:=
=
:=
1
390.512 cm
Pmax1
S1
L3 474.342 cm
Pmax3
S3
λ =
=
gr
103.193
R
20.5
2
cm
P
= −
= −
max1
89.88 kN
Pmax3
85.331 kN
Dla przekroju złożonego z dwóch kątowników 65x65x6a, grubość przewiązki 10
2
i
:=
⋅
:=
⋅
min
2.48 cm
A3s
15.10 cm
L
π2⋅
L
π2⋅
λ
1
:=
λ =
E
:=
λ
3
:=
λ =
E
:=
1
1
157.465
Rkr1
3
3
191.267
Rkr3
imin
λ 2
imin
λ 2
1
3
kN
kN
R
=
:=
⋅
=
:=
⋅
kr1
8.16
Pkr1
Rkr1 A3s
Rkr3 5.531
Pkr3
Rkr3 A3s
2
2
cm
cm
P
=
=
kr1
123.215 kN
Pkr3 83.512 kN
Przekrój nie spełnia wymagań Dla przekroju złożonego z dwóch kątowników 65x65x7, grubość przewiązki 10
2
i
:=
⋅
:=
⋅
min
2.47 cm
A3s
17.40 cm
L
π2⋅
L
π2⋅
λ
1
:=
λ =
E
:=
λ
3
:=
λ =
E
:=
1
1
158.102
Rkr1
3
3
192.041
Rkr3
imin
λ 2
imin
λ 2
1
3
kN
kN
R
=
:=
⋅
=
:=
⋅
kr1
8.094
Pkr1
Rkr1 A3s
Rkr3 5.486
Pkr3
Rkr3 A3s
2
2
cm
cm
P
=
=
kr1
140.84 kN
Pkr3 95.458 kN
A :=
3
A3s
Zadanie 3
Obliczenie przemieszczeń w węźle 3(K) Reakcje
1
1
R
:=
:=
1j
V5j
2
2

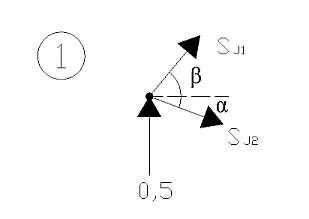
Obliczenie sił podłużnych w kratownicy Węzeł 1
R
−
⋅
+
⋅
1j
S2j sinα S1j sinβ = 0
S ⋅
+
⋅
2j cosα
S1j cosβ = 0
S
= −
1j
0.496
S
=
2j
0.339
Węzeł 2
S
− ⋅
−
⋅
1j sinβ
S3j cosγ = 0
S
+
⋅
−
⋅
4j
S3j sinγ S1j cosβ = 0
S
=
3j
0.402
S
= −
4j
0.444
Z symetri obciążenia i geometri: S
:=
5j
S3j
S
:=
6j
S2j
S
:=
7j
S1j
Węzeł 3 - spr
S ⋅
+
⋅
+
⋅
+
⋅
− =
2j sinα
S3j cosγ S5j cosγ S6j sinα 1 0
OK!
1
1
1
w :=
⋅( ⋅ ⋅ + ⋅ ⋅ ) +
⋅( ⋅ ⋅ ) +
⋅( ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅
k
L2 S2 S2j L6 S6 S6j
L4 S4 S4j
L1 S1 S1j L3 S3 S3j L5 S5 S5j L7 S7 S
E⋅A
⋅
⋅
1
E A2
E A3
w =
k
0.148 cm
a) Macierze sztywności prętów w układzie lokalnym Pręt 1
250⋅cm
300⋅cm
c :=
s :=
L
L
1
1
2
2
c
c⋅s
c
−
c
− ⋅s
374.35
449.221
3
− 74.35
4
− 49.221
E⋅A
2
2
3
c
⋅s
s
c
− ⋅s
s
−
449.221
539.065
4
− 49.221 5
− 39.065 kN
K
:=
⋅
K
=
e1
e1
L
2
2
3
− 74.35
4
− 49.221 374.35
449.221 cm
1
c
−
c
− ⋅s c
c⋅s
4
− 49.221 5
− 39.065 449.221 539.065
2
2
c
− ⋅s
s
−
c⋅s
s
Pręt 2
400⋅cm
c :=
1
− 50⋅cm
s
L
:=
2
L2
2
2
c
c⋅s
c
−
c
− ⋅s
295.336
1
− 10.751 2
− 95.336 110.751
E⋅A
2
2
1
c
⋅s
s
c
− ⋅s
s
−
1
− 10.751
41.532
110.751
4
− 1.532 kN
K
:=
⋅
K
=
e2
e2
L
2
2
2
− 95.336 110.751 295.336
1
− 10.751 cm
2
c
−
c
− ⋅s c
c⋅s
110.751
4
− 1.532
1
− 10.751 41.532
2
2
c
− ⋅s
s
−
c⋅s
s
Pręt 3
1
− 50cm
c :=
450cm
s
L
:=
3
L3
2
2
c
c⋅s
c
−
c
− ⋅s
75.199
2
− 25.597
7
− 5.199 225.597
E⋅A
2
2
3
c
⋅s
s
c
− ⋅s
s
−
2
− 25.597 676.791
225.597
6
− 76.791 kN
K
:=
⋅
K
=
e3
e3
L
2
2
7
− 5.199 225.597
75.199
2
− 25.597 cm
3
c
−
c
− ⋅s c
c⋅s
225.597
6
− 76.791 2
− 25.597 676.791
2
2
c
− ⋅s
s
−
c⋅s
s
Pręt 4
c := 1
s := 0
2
2
c
c⋅s
c
−
c
− ⋅s
479.7 0
4
− 79.7 0
E⋅A
2
2
2
c
⋅s
s
c
− ⋅s
s
−
0
0
0
0
kN
K
:=
⋅
K
=
e4
e4
L
2
2
4
− 79.7 0 479.7 0 cm
4
c
−
c
− ⋅s c
c⋅s
0
0
0
0
2
2
c
− ⋅s
s
−
c⋅s
s
150cm
450cm
c :=
s :=
L
L
5
5
2
2
c
c⋅s
c
−
c
− ⋅s
75.199
225.597
7
− 5.199
2
− 25.597
E⋅A
2
2
3
c
⋅s
s
c
− ⋅s
s
−
225.597
676.791
2
− 25.597 6
− 76.791 kN
K
:=
⋅
K
=
e5
e5
L
2
2
7
− 5.199
2
− 25.597 75.199
225.597 cm
5
c
−
c
− ⋅s c
c⋅s
2
− 25.597 6
− 76.791 225.597 676.791
2
2
c
− ⋅s
s
−
c⋅s
s
Pręt 6
400cm
c :=
150cm
s
L
:=
6
L6
2
2
c
c⋅s
c
−
c
− ⋅s
295.336
110.751
2
− 95.336 1
− 10.751
E⋅A
2
2
1
c
⋅s
s
c
− ⋅s
s
−
110.751
41.532
1
− 10.751
4
− 1.532 kN
K
:=
⋅
K
=
e6
e6
L
2
2
2
− 95.336 1
− 10.751 295.336 110.751 cm 6
c
−
c
− ⋅s c
c⋅s
1
− 10.751
4
− 1.532 110.751
41.532
2
2
c
− ⋅s
s
−
c⋅s
s
Pręt 7
2
− 50cm
c :=
300cm
s
L
:=
7
L7
2
2
c
c⋅s
c
−
c
− ⋅s
374.35
4
− 49.221
3
− 74.35 449.221
E⋅A
2
2
3
c
⋅s
s
c
− ⋅s
s
−
4
− 49.221 539.065
449.221
5
− 39.065 kN
K
:=
⋅
K
=
e7
e7
L
2
2
3
− 74.35 449.221
374.35
4
− 49.221 cm
7
c
−
c
− ⋅s c
c⋅s
449.221
5
− 39.065 4
− 49.221 539.065
2
2
c
− ⋅s
s
−
c⋅s
s
Pręt 8
c := 0
s := 1
2
2
c
c⋅s
c
−
c
− ⋅s
0
0
0
0
2
2
3
3
E⋅A
3
c
⋅s
s
c
− ⋅s
s
−
0
1.189
× 10
0
1
− .189 × 10
kN
K
:=
⋅
K
=
e8
e8
L
2
2
0
0
0
0
8
cm
c
−
c
− ⋅s c
c⋅s
3
3
2
2
0
1
− .189 × 10 0 1.189 × 10
c
− ⋅s
s
−
c⋅s
s
c := 1
s := 0
2
2
c
c⋅s
c
−
c
− ⋅s
575.64 0
5
− 75.64 0
E⋅A
2
2
2
c
⋅s
s
c
− ⋅s
s
−
0
0
0
0
kN
K
:=
⋅
K
=
e9
e9
L
2
2
5
− 75.64 0 575.64 0 cm
9
c
−
c
− ⋅s c
c⋅s
0
0
0
0
2
2
c
− ⋅s
s
−
c⋅s
s
Pręt 10
c := 1
s := 0
2
2
c
c⋅s
c
−
c
− ⋅s
575.64 0
5
− 75.64 0
E⋅A
2
2
2
c
⋅s
s
c
− ⋅s
s
−
0
0
0
0
kN
K
:=
⋅
K
=
e10
e10
L
2
2
5
− 75.64 0 575.64 0 cm
10
c
−
c
− ⋅s c
c⋅s
0
0
0
0
2
2
c
− ⋅s
s
−
c⋅s
s
Pręt 11
c := 0
s := 1
2
2
c
c⋅s
c
−
c
− ⋅s
0
0
0
0
2
2
3
3
E⋅A
3
c
⋅s
s
c
− ⋅s
s
−
0
1.189
× 10
0
1
− .189 × 10
kN
K
:=
⋅
K
=
e11
e11
L
2
2
0
0
0
0
11
cm
c
−
c
− ⋅s c
c⋅s
3
3
2
2
0
1
− .189 × 10 0 1.189 × 10
c
− ⋅s
s
−
c⋅s
s
b) Macierz sztywności kratownicy K
:=
( , , , , ) + ( , , , , ) + ( , , , , ) 11
sb Ke1 1 2 1 2
sb Ke2 1 2 1 2
sb Ke8 1 2 1 2
669.687
338.469 kN
K
=
11
3
338.469 1.77 × 10 cm
K
:=
( , , , , ) + ( , , , , ) + ( , , , , ) + ( , , , , ) 22
sb Ke1 3 4 3 4
sb Ke3 3 4 3 4
sb Ke4 1 2 1 2
sb Ke9 3 4 3 4
3
1.505
× 10
223.624
kN
K
=
22
3
cm
223.624
1.216 × 10
K
:=
( , , , , ) + ( , , , , ) + ( , , , , ) + ( , , , , ) 33
sb Ke2 3 4 3 4
sb Ke3 1 2 1 2
sb Ke5 1 2 1 2
sb Ke6 1 2 1 2
− 14
741.07
1.863
× 10
kN
K
=
33
− 14
3
cm
1.863 × 10
1.437 × 10
K
:=
( , , , , ) + ( , , , , ) + ( , , , , ) + (
, , , , )
44
sb Ke4 3 4 3 4
sb Ke5 3 4 3 4
sb Ke7 3 4 3 4
sb Ke10 1 2 1 2
3
1.505
× 10
2
− 23.624 kN
K
=
44
3
cm
2
− 23.624 1.216 × 10
K
:=
( , , , , ) + ( , , , , ) + (
, , , , )
55
sb Ke6 3 4 3 4
sb Ke7 1 2 1 2
sb Ke11 1 2 1 2
669.687
3
− 38.469 kN
K
=
55
3
3
− 38.469 1.77 × 10 cm
575.64
0
kN
K
:=
( , ,4,3,4 + ( , ,2,1,2
K
) sb K
)
=
66
sb Ke8 3
e9 1
66
3
0
1.189 × 10 cm
575.64
0
kN
K
:=
(
, , 4, 3, 4 + (
, , 4, 3, 4
K
) sb K
)
=
77
sb Ke10 3
e11 3
77
3
0
1.189 × 10 cm
K
:=
( , ,2,3,4
3
− 74.35
4
− 49.221 kN
)
12
sb Ke1 1
K
=
12
4
− 49.221 5
− 39.065 cm
2
− 95.336 110.751 kN
K
:=
( , ,2,3,4
K
)
=
13
sb Ke2 1
13
110.751
4
− 1.532 cm
0 0 kN
0 0 kN
K
:=
⋅
K
=
14
14
0 0 cm
0 0 cm
0 0 kN
0 0 kN
K
:=
⋅
K
=
15
15
0 0 cm
0 0 cm
0
0
kN
K
:=
( , ,2,3,4
K
)
=
16
sb Ke8 1
16
3
0
1
− .189 × 10 cm
0 0 kN
0 0 kN
K
:=
⋅
K
=
17
17
0 0 cm
0 0 cm
7
− 5.199 225.597 kN
K
:=
( , ,2,3,4
K
)
=
23
sb Ke3 1
23
225.597
6
− 76.791 cm
4
− 79.7 0 kN
K
:=
( , ,2,3,4
K
)
=
24
sb Ke4 1
24
0
0 cm
0 0 kN
K
:=
⋅
K
=
25
25
0 0 cm
0 0 cm
5
− 75.64 0 kN
K
:=
( , ,2,3,4
K
)
=
26
sb Ke9 1
26
0
0 cm
0 0 kN
0 0 kN
K
:=
⋅
K
=
27
27
0 0 cm
0 0 cm
7
− 5.199
2
− 25.597 kN
K
:=
( , ,4,1,2
K
)
=
34
sb Ke5 3
34
2
− 25.597 6
− 76.791 cm
2
− 95.336 1
− 10.751 kN
K
:=
( , ,4,1,2
K
)
=
35
sb Ke6 3
35
1
− 10.751
4
− 1.532 cm
0 0 kN
0 0 kN
K
:=
⋅
K
=
36
36
0 0 cm
0 0 cm
0 0 kN
0 0 kN
K
:=
⋅
K
=
37
37
0 0 cm
0 0 cm
3
− 74.35 449.221 kN
K
:=
( , ,2,3,4
K
)
=
45
sb Ke7 1
45
449.221
5
− 39.065 cm
0 0 kN
0 0 kN
K
:=
⋅
K
=
46
46
0 0 cm
0 0 cm
5
− 75.64 0 kN
K
:=
(
, , 4, 1, 2
K
)
=
47
sb Ke10 3
47
0
0 cm
0 0 kN
0 0 kN
K
:=
⋅
K
=
56
56
0 0 cm
0 0 cm
0
0
kN
K
:=
(
, , 2, 3, 4
K
)
=
57
sb Ke11 1
57
3
0
1
− .189 × 10 cm
0 0 kN
0 0 kN
K
:=
⋅
K
=
67
67
0 0 cm
0 0 cm