Lista 4

Siły bezwładności

81. Jaką minimalną siłą naleŜy

Ŝ

y dzi

z ałać na ciało A o masie M A (patr

t z

z rys

y unek)

k , aby

b

y

ciało B o masie M B nie porusza

z ło si

s ę względem niego, jeśli:

i a) ws

w pół

ó czy

z n

y nik

k

tarcia między

z

y A

A i B

B wy

w n

y osi f AB, gdy A porusza się po idea e lni

n e gł

g ad

a ki

k ej

e

powi

w erzc

z hni

n ? b)

b ws

w pół

ó czy

z n

y nik

k tarci

c a mi

m ędzy A i B wynosi f AB , a między

y A

A i pozi

z omą powierzchnią

wynosi f? Obliczenia wykonać dl

d a f AB = 0,6, f = 0,4, M A = 20 kg i MB = 2 kg.

Rozwiązanie:

82. Wahadło o masie m wi

w si na podst

s awc

w e

c umo

m cowa

w nej

e na wó

w zk

z u

k . Zn

Z aleźć ki

k erunek

k nici wa

w hadł

d a, tj

t .

.

kąt α nici z pio

i nem

m oraz

z jej

e napr

p ęŜenie T w przypadkach: a) wózek porusza się ru r chem

m jed

e nost

s aj

a nym

y

m

po płaszczyźnie pozi

z ome

m j,

, b) wó

w ze

z k

k porusza

z się po płaszczyźnie pozi

z ome

m j z

z przy

z s

y piesze

z niem

m a, c)

wózek stacza się s

wo

w bodni

n e

i z

z równ

w i poc

o hył

y ej

e , kt

k ór

ó a t

w

t o

w rzy

z

y kąt β z poziomem.

Rozwiązanie:

83. O jaki kąt odchyli się pozi

z om

m cieczy

z

y prze

z wo

w Ŝonej

e w

w samo

m chodzi

z e cys

y te

t rnie

i , gd

g y

y samo

m chód

d

hamuje z opóźnieniem 5 m/s2 (g

g = 10 m/

m s).

Rozwiązanie:

84. Wyznaczyć wartości sił odśrod

o ko

k wy

w c

y h dzi

z ałaj

a ących na człowieka znajdujące

c go

g się: a) na równiku;

b) na powierzchni Ziemi porusza

z j

a ącej się wokół Słońca. Dane: promień Zi

Z emi

m 6400 km,

m średnia

odległość Ziemi od Słońca

c w

y

w n

y osi 150 ml

m n. km.

m

Rozwiązanie:

85. Wyznaczyć nacisk

k ciała

ł pilot

o a o ma

m sie M na fotel samolotu wykonującą pęt

ę l

t ę

l o promieniu R = 6

km leŜącą w płaszczyźnie pionowe

w j

e , gd

g y

y samo

m lot jest

s :

t a) w

w naj

a ni

n Ŝszy

z m

m punkc

k ie okr

k ęgu (fotel jest pod

ciałem pilota) a prędkość samo

m lotu wy

w n

y osi 280 m/

m s; b) w

w najwy

w Ŝszym

m punkc

k ie pętli (fotel jest nad

pilotem) a prędkość samo

m lotu wy

w n

y osi 120 m/s. Obliczenia wykonać dla M = 62

2 kg.

g W jakim punkcie

pętli i przy jakich wartościac

a h pod

o anyc

y h par

a ame

m tró

r w

w pilot

o pr

p ze

z z

z chwi

w lę zn

z a

n j

a dzi

z e się w stanie

niewaŜkości?

Rozwiązanie:

86. Współczynnik tarcia między

y torem

m a opona

n mi

m samo

m chodu wy

w n

y osi

i 0,8.

. Z

Z jaką maksymalną

prędkością moŜe ten samo

m chód poko

k nać bez poślizgu zakręt o promieniu 40 m?

Rozwiązanie:

87. Na cało o masie M poruszający się w powietrzu z prędkością v nad powierzchnią Ziemi działa oprócz siły grawitacji, siła bezwładności F C = 2 M v×ω, zwana siłą Coriolisa, gdzie ω jest prędkością kątową ruchu obrotowego Ziemi wokół osi płn-płd., przy czym wektor ω jest skierowany od bieguna płd. Ziemi do jej bieguna płn. Uzasadnić, Ŝe ciała wykonujące rzut ukośny na półkuli płn. odchylają się od pierwotnego kierunku zawsze w prawo względem wektora prędkości v. Jaką regułę moŜna stąd wysnuć dla ciał wykonujących rzut ukośny na półkuli płd? Dlaczego ciała rzucone pionowo w dół, niezaleŜnie od półkuli, odchylają się na wschód, tj. nie spadają pionowo w dół? Wyobraź sobie idealnie gładką rurkę o średnicy d i wysokości H ustawioną pionowo na równiku, w której spada swobodnie i bez tarcia kulka o średnicy d. Z rurki odpompowano powietrze. Jak zaleŜy od czasu siła wywierana przez spadającą kulkę na boczną ściankę rurki?

Rozwiązanie:

88. Wiadro z wodą wprawiono w ruch po okręgu o promieniu R leŜący w płaszczyźnie pionowej. Jaka jest minimalna wartość prędkości wiadra w najwyŜszym punkcie toru ruchu, dla której woda nie będzie wylewała się z niego?

Rozwiązanie:

89. Największy i najmniejszy pozorny cięŜar ciała człowiek stojącego na wadze umieszczonej w windzie wynosi odpowiednio 591 N i 391 N. Zakładając, Ŝe wartości przyspieszenia i opóźnienia (przy hamowaniu) windy podczas jej ruchu w górę są takie same wyznaczyć rzeczywistą masę człowieka oraz przyspieszenie/opóźnienie windy.

Rozwiązanie:

90. Samochód porusza się ze stałą prędkością v po drodze połoŜonej na wzgórzu o promieniu krzywizny w najwyŜszym punkcie równym 20 m. Wyznaczyć v, jeśli na szczycie wzgórza nacisk kół

samochodu na drogę jest zaniedbywalnie mały.

Rozwiązanie:

Dynamika ruchu krzywoliniowego

91. Jarek o masie M = 40 kg buja się na huśtawce zawieszonej na dwóch linkach o długości L = 2 m kaŜda. W najniŜszym punkcie toru P siła napręŜenia kaŜdej z linek wynosi 300 N. Wyznaczyć prędkość i przyspieszenie dośrodkowe Jarka oraz siłę jego nacisku na deskę huśtawki w punkcie P

toru.

Rozwiązanie:

92. Samochód porusza się po łuku drogi o promieniu R. Powierzchnia drogi jest nachylona pod kątem α względem poziomu w kierunku do wnętrza zakrętu. Współczynnik tarcia wynosi f. Pokazać, Ŝe maksymalna prędkość, przy której samochód nie wypadnie z zakrętu na skutek poślizgu spełnia równość ( v max)2 = R g( f+ tgα)/(1 -f tgα).

Rozwiązanie:

93. Samochód wpadł w poślizg na poziomym zakręcie o promieniu krzywizny 200 m, przed którym stał znak ograniczenia prędkości do 40 km/h. O ile przekroczył kierowca dozwoloną prędkość, jeśli współczynnik tarcia między oponami i jezdnią wynosił 4/5? Wynik podać w km/h.

Rozwiązanie:

94. Rowerzysta jedzie ze stałą prędkością v = 10 m/s po torze kołowym. Kąt nachylenia płaszczyzny roweru do poziomu wynosi α =60˚. Oblicz promień toru.

Rozwiązanie:

95. Droga ma łagodny płaski zakręt o promieniu R = 100 m. Jakie powinno być ograniczenie prędkości na tym zakręcie (wyraŜone w km/h) jeśli w niesprzyjających warunkach współczynnik tarcia µ= 0,2 ?

Rozwiązanie:

96. Mała kulka stacza się po rynnie zakończonej pionową pętlą o promieniu r. Z jakiej wysokości kulka ta powinna się stoczyć, aby nie odpaść od pętli?

Rozwiązanie:

97. Z wierzchołka gładkiej kuli o promieniu R zsuwa się bez tarcia małe ciało. Wyznacz połoŜenie punktu, w którym wspomniane ciało oderwie się od powierzchni kuli.

Rozwiązanie:

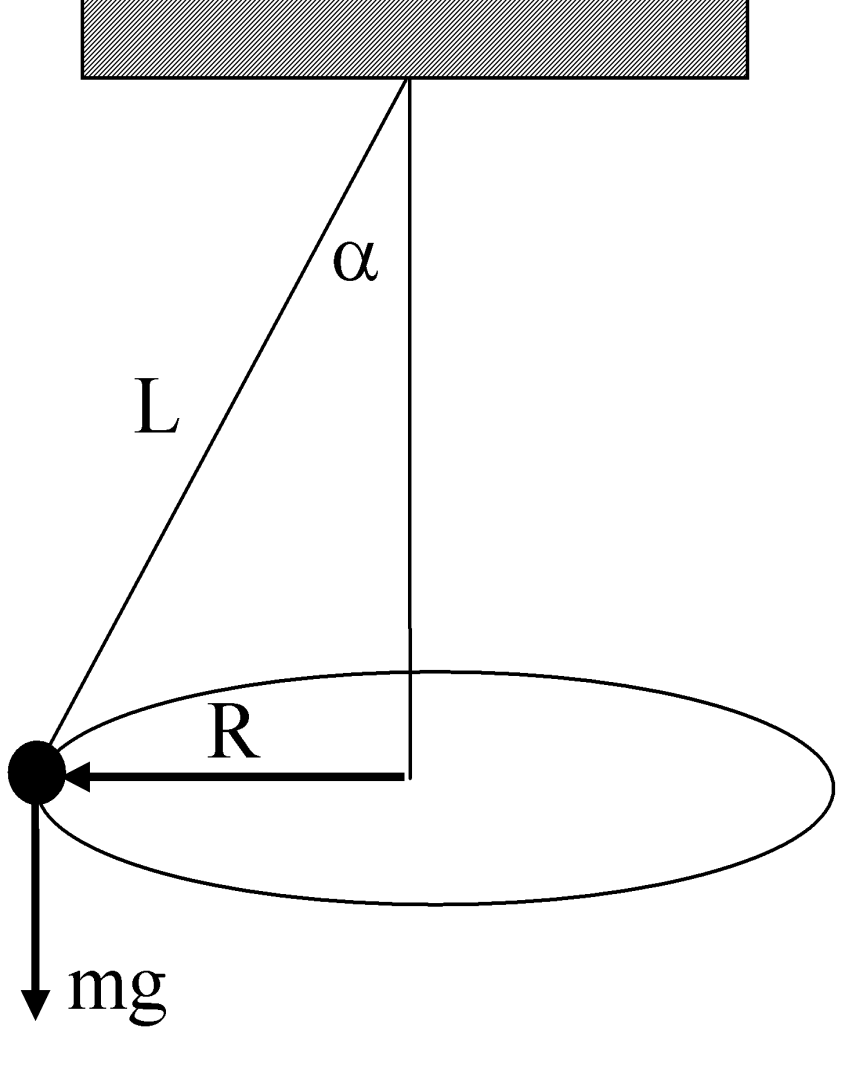
98. Wahadło matematyczne moŜna wprawić w ruch po okręgu (rysunek), otrzymujemy wówczas wahadło stoŜkowe. ZałóŜmy, ze wychylenie takiego wahadła wynosi α. Oblicz okres obiegu takiego wahadła.

Rozwiązanie:

99. Punkt materialny rozpoczyna ruch po okręgu o promieniu R ze stałym przyspieszeniem kątowym ε , jednostką ε jest s-2.Po jakim czasie siła dośrodkowa będzie n razy większa od siły stycznej?

Rozwiązanie:

100. CięŜarek o masie m zawieszony na nici o długości d obraca się po okręgu ruchem jednostajnym w płaszczyźnie poziomej. W czasie ruchu nić odchylona jest od pionu o kąt α. Oblicz siłę napręŜenia nici.

Rozwiązanie:

101. Słońce znajduje się w odległości 23 000 lat świetlnych od środka Drogi Mlecznej i porusza się wokół tego środka po okręgu z prędkością 250 km/s. Ile czasu zajmuje Słońcu pełny obieg? Ile takich obiegów wykonało Słońce, które powstało 4,5 mld lat temu. Wskazówka jeden rok świetlny do droga, którą przebywa światło poruszające się w próŜni z prędkością 300 000 km/h w czasie jednego roku, który liczy w przybliŜeniu 10π mln sekund.

Rozwiązanie:

102. Statek kosmiczny pokonuje w przestrzeni kosmicznej łuk okręgu o promieniu 3220 km, poruszając się ze stałą wartością prędkości 29 000 km/h. Jaka jest wartość jego: a) prędkości kątowej?

b) przyspieszenia dośrodkowego? c) przyspieszenia stycznego?

Rozwiązanie:

103. Wyznaczyć zaleŜności od czasu wartości sił: całkowitej, stycznej i dośrodkowej (składowych tej pierwszej) działających na ciało o masie M wykonujące rzut: A) poziomy; B) ukośny. Wskazówka: wyznaczyć najpierw wartości przyspieszeń: całkowitego, stycznego i dośrodkowego. Czy moŜna wyznaczyć zaleŜność od czasu promienia krzywizny toru rzutu ukośnego i poziomego?

Rozwiązanie:

***