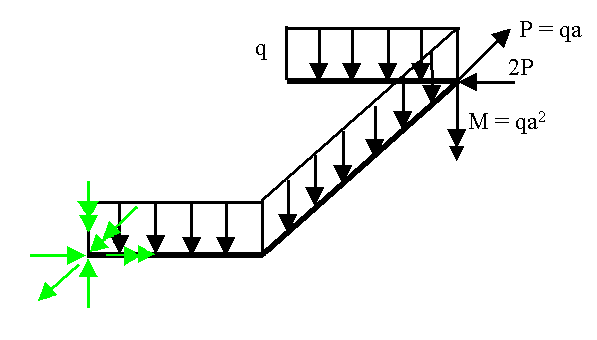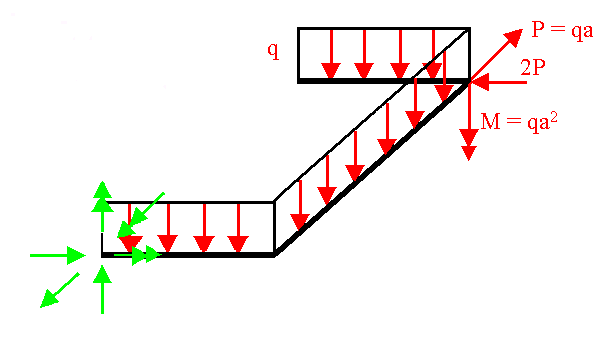
Przykład 5.2. Dźwigar załamany w planie Wyznaczyć reakcje w dźwigarze załamanym w planie o podanym schemacie.
Rozwiązanie.
Uwalniamy układ z więzów wprowadzając odpowiadające im reakcje.
M Ax
M Az
RAy
R
R
M
Ax
Az
Ay
Przedstawiony dźwigar jest całkowicie utwierdzony całkowicie (zamocowanie sztywne) w punkcie A. Nie znamy sześciu reakcji: RAx, RAy, RAz,, MAx, MAy i MAz . Dla przedstawionej ramy można zapisać sześć warunków równowagi. Zatem układ jest statycznie wyznaczalny.
Dowolny przestrzenny układ sił P znajduje się w równowadze, jeżeli sumy rzutów i
wszystkich sił na trzy osie układu są równe zeru i sumy momentów wszystkich sił względem trzech osi układu są równe zeru:
∑ P = ,0
P
P
ix
∑ = ,0
iy
∑ = 0
iz
∑ M = ,0
M
M
ix
∑
= ,
0
iy
∑
= 0
iz
Po sprawdzeniu, że układ sił jest statycznie wyznaczalny i przyjęciu układu współrzędnych xyz, zapisujemy równania równowagi korzystając ze wzorów zapisanych powyżej.
∑ P = 0
R − P = 0
→
R = P = qa ix
Ax
Ax
∑ P = 0
R − 2 P = 0
→
R = 2 P = 2 qa iy
Ay
Ay
∑ P = 0
R − q + 2 +
= 0
→
= 4
iz
Az
( a a a)
R
qa
Az
a
2
∑ M = 0
M
− 2 ⋅ q ⋅ a ⋅ − q ⋅ 2 a ⋅ a = 0
→
M
= 3 qa
ix
Ax
2
Ax
2
∑ M = 0
M
− q ⋅ a ⋅ 2 a − q ⋅ 2 a ⋅ a = 0
→
M
= 4 qa
iy
Ay
Ay
2
∑ M = 0
M
+ 2 P ⋅ 2 a + Pa − M = 0
→
M
= M − 5 Pa = −4 qa iz
Az
Az
W celu sprawdzenia poprawności obliczeń korzystamy z warunku równowagi, z którego nie korzystaliśmy poprzednio
∑ M = 0 − M − M + R ⋅ a + R ⋅2 a = 0 →
2
− qa − 4 2
2
qa + qa + 4
2
qa = 0
iz 1
Az
Ay
Odp.
2
M
= 4 qa
Az
2
M
= 3 qa
Ax
R = 2 qa
Ay
2
M
= 4 qa
Ay
R = qa
Ax
R = 4 qa
Az
2