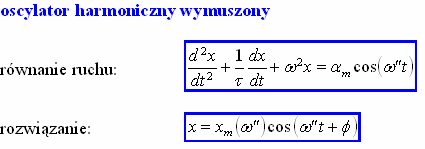
Oscylator harmoniczny wymuszony
Równanie ruchu, rozwiązanie
opis formalny:
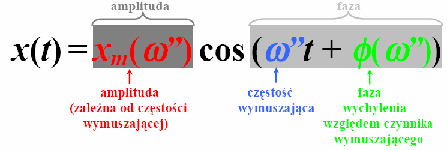
struktura rozwiązania:
φ ( ω” ) – wg definicji kąt, o jaki maksimum wychylenia wyprzedza maksimum czynnika wymuszającego
należy określić nieznane parametry xm( ω” ) i φ ( ω” ) − w tym celu należy podstawić rozwiązanie do równania ruchu
pojęcia „wychylenie” i „prędkość” należy rozumieć ogólniej; mogą reprezentować różne wielkości fizyczne, np.
x – wychylenie liniowe, wychylenie kątowe, ładunek elektryczny, υ – prędkość liniową, prędkość kątową, natężenie prądu elektrycznego) obliczamy pierwszą pochodną dx/ dt (wyłączamy czynnik stały przed znak pochodnej, korzystamy ze wzoru na pochodną funkcji złożonej u ( ( f '
)) = '
u ( f ) ⋅ f ' ): dx = d ( x cos(
m
ω" t + φ)) = ω
− " x sin (
m
ω" t + φ)
dt
dt
obliczamy drugą pochodną d 2 x/ dt 2 (zasady j.w.): 2
d x
d dx
d
=
=
( ω
− " x sin (
m
ω' t + φ))
2
= ω
− " x cos(
m
ω' t + φ)
2
dt
dt dt
dt
podstawiamy wyrażenia na dx/ dt i d 2 x/ dt 2 do równania ruchu: 1
− "
ω 2 x cos( "
ω t + φ) −
"
ω x sin( "
ω t + φ) + ω 2 x cos( "
ω t + φ) = α cos "
ω t
m
m
m
m
τ
po wykorzystaniu wzorów na funkcje trygonometryczne sumy kątów:
n(
+ β ) = sin α cos β + cos α sin β
co α
s( + β ) = cos α cos β − sin α sin β
otrzymujemy:
ω
( 2 − "
ω 2 ) x cos "
ω t cos φ − ω
( 2 − "
ω 2 ) x sin "
ω t sin φ +
m
m
"
ω
"
ω
−
x sin "
ω t cos φ −
x cos "
ω t sin φ = α cos "
ω t
m
m
m
τ
τ
porządkujemy wyrazy ze względu na cos ω”t i sin ω”t
"
ω
( 2
2
ω − "
ω ) x cos φ
φ α
ω
m
−
x sin
m
−
cos " t
m
+
τ
(1)
"
ω
− ( 2
2
ω − "
ω ) x sin φ
φ
ω
m
+
x cos
sin " t
m
= 0
τ
warunkiem spełnienia równania (1) jest jednoczesne zerowanie współczynników przy cos ω”t i sin ω”t:
"
ω
( 2
2
ω − "
ω ) x cos φ
φ α
m
−
x sin
m
− m = 0
τ
(2)
ω"
( 2
2
ω − ω" ) x sin m
φ +
x cos
m
φ = 0
τ
(3)
z (3):
"
ω τ
2
2
ω"
ω
(
− ω" )sin φ = −
cos φ
tg φ = −
τ
→
2
2
ω −
(4)
"
ω
z tg φ obliczamy sin φ i cos φ (można skorzystać z gotowych wzorów zamieszczonych np.
w tablicach matematycznych):
tg φ
1
sin φ =
,
cos φ =
tg2 φ + 1
tg2 φ + 1
podstawiamy (4) do powyższych wzorów: ω" τ
− 2
2
ω − ω
ω" τ
sin φ
"
=
= −
2
2
2 2
2
(
ω" τ
ω − ω" ) + ( ω" τ )
−
+1
2
2
ω − ω"
2
2
1
ω − ω"
cos φ =
=
2
2
2 2
2
(
ω" τ
ω − ω" ) + ( ω" τ )
−
+1
2
2
ω − ω"
podstawiamy wyrażenia na sin φ i cos φ do (2):
2
2
ω − "
ω
( 2
2
ω − "
ω )
xm
+
( 2
2
ω − "
ω )2 + ( "
ω τ )2
"
ω
"
ω τ
−
α
m
x
−
− m = 0
τ
( 2
2
ω − "
ω )2 + ( "
ω τ )2
1
[ ω 2
(
− "
ω 2 2
) + ( "
ω τ 2
) ] x
= α
m
m / : ...
ω 2
(
− "
ω 2 2
) + ( "
ω τ 2
)
α
x
m
=
m
(5)
2
2 2
2
( ω − ω" ) + ( ω" τ ) α ω
υ
"
m
=
m
2
2
2
2
(6)
( ω − ω" ) + ( ω" τ ) Częstość rezonansowa
• dla wychylenia
2
d x
d x
x
m = ,
m <
m – max →
0
0
2
d "
ω
d "
ω
wystarczy obliczyć pochodne wyrażenia podpierwiastkowego w mianowniku α
x
m
=
m
X ( "
ω )
2
d X
d X
x
= ,
>
m – max →
0
0
2
d "
ω
d "
ω
obliczamy pierwszą pochodną dX / dω”
d X = d [
d
d
( 2
ω −
2
"
ω )2 + ( "
ω τ )2]=
[( 2
ω −
2
"
ω )2]+
[( "ω τ)2]=
d "
ω
d "
ω
d "
ω
d "
ω
2
2
1
2
2
= (
2 ω − "
ω )(−2 "
ω ) + 2( "
ω τ 1
)( τ ) = 2 "
ω − (2 ω − "
ω )
2
τ
obliczamy drugą pochodną d 2 X / dω” 2
2
d X
d
1
2
2
=
2 "
ω
2( ω
"
ω )
2
−
−
2
=
d "
ω
d "
ω
τ
d
1
2
2
=
d
(2 "
ω ) ⋅
− 2( ω − "
ω ) + [2 "
ω ]
1
2
2
⋅
− (
2 ω − "
ω ) =
2
2
d "
ω
τ
d "
ω τ
1
2
2
= 2
− (
2 ω − "
ω ) + 2 "
ω ⋅(−2) ⋅ (−2 "
ω ) =
2
τ
1
2
2
2
= 2 − (2 ω − "
ω ) + 4 "
ω
2
τ
d X
1
= 0
2 "
ω = 0 ∨
− (
2
2
2
ω − "
ω ) =
d "
ω
→
0
2
τ
pierwszy przypadek nie jest interesujący (zerowa częstość wymuszająca – brak drgań wymuszonych), zatem
d X
1
= 0
− 2( 2
2
ω − "
ω ) =
d "
ω
→
0
2
τ
po podstawieniu do wyrażenia na drugą pochodną: 1
2
d X
− (
2
2
2
ω − "
ω ) = 0 →
= 2 ⋅ 4 2
"
ω > 0
2
τ
2
d "
ω
tzn.
2
d X
d X
= 0 ,
> 0
2
d "
ω
→ X – min → xm – max d "
ω
obliczamy wartość ω” spełniającą warunek 1
1
2
1
− (
2
2
2
ω − "
ω ) = 0 → 2
2
ω − ω" =
→ ω"rez = ω −
(7)
2
τ
2
2
2 τ
2 τ
• dla prędkości
2
d υ
d υ
υ
m = 0 ,
m <
m – max →
0
2
d "
ω
d "
ω
wystarczy licznik i mianownik podzielić przez ω”
α
υm =
m
[
( ω ω" ) − ]2
2
2
1
+ 1
( τ )
i obliczyć pochodne wyrażenia podpierwiastkowego w mianowniku αm
υ =
m
V ( "
ω )
2
d V
d V
υ
= ,
>
m – max →
0
0
2
d "
ω
d "
ω
obliczamy pierwszą pochodną dV / dω”
2
2
2
2
2
2
d V
d
ω
1
d
ω
d
1
=
−1 + =
−1
+
=
d "
ω
d "
ω "
ω
τ d "
ω "
ω
d "
ω
τ
2
2
ω
ω
1
ω
ω
= 2
−1 ⋅ 2
⋅ −
= −4
−1 ⋅
=
2
3
"
ω
"
ω
"
ω
"
ω
"
ω
2
( ω
"
ω ) −1
= −4 ω
3
"
ω
obliczamy drugą pochodną d 2 V / dω” 2 – korzystamy ze wzoru na pochodną ilorazu
′
f
f ' g − f '
g
=
:
2
g
g
2
d V
d
( ω ω" )2 − 1
=
ω
2
− 4
3
=
ω
d "
ω
d "
ω"
2
2
4 ω
d
ω
= −
ω
d
−
1 ω"
ω"
6
[⋅ 3]
− −
1 ⋅
[ 3]=
ω" dω" ω"
ω"
ω
d "
2
4 ω ω
ω
= −
ω
ω"
ω"
6
2
⋅−
[⋅
3
2
]
−
−
1 [3 2]
⋅
=
ω" ω" ω"
ω"
2
= − 4 ω −
ω
2 2
ω
3
2
ω"
−
−
1
6
ω"
ω"
2
d V
ω
= 0
−1 =
d "
ω
→
0
"
ω
po podstawieniu do wyrażenia na drugą pochodną: 2
d V
4 ω
= −
⋅(−2 2
ω ) > 0
2
6
dω"
ω"
2
d V
d V
= 0 ,
> 0
2
d "
ω
→ V – min → υm – max d "
ω
obliczamy wartość ω” spełniającą warunek 2
ω
−1 = 0 → ω"rez = ω
(8)
"
ω