X1i
ni
Środek przed Xiz
ia
- łu
srednia (Xi - sr)^2 (Xi - sr)^2 * ni 10
20
5
15
-21,6
466,56
2332,8
S^2
208,3
20
30
7
25
-11,6
134,56
941,92
30
40
11
35
-1,6
2,56
28,16
S
14,4
40
50
6
45
8,4
70,56
423,36
50
60
4
55
18,4
338,56
1354,24
60
70
3
65
28,4
806,56
2419,68
Suma
36
7500,16
S^2 = 7500,16/36
S = pierwiastek z S^2
C
5
5
5
5
5
5
5
5
5
5
4
10
5
6
0
A
Xi - Xsr
(Xi - Xsr)^2
B
Xi - Xsr
(Xi - Xsr)^2
C
Xi - Xsr
(Xi - Xsr)^2
5
0
0
5
0
0
5
0
0
5
0
0
5
0
0
5
0
0
5
0
0
5
0
0
5
0
0
5
0
0
4
-1
1
10
5
25
5
0
0
6
1
1
0
-5
25
0
2
50
5
5
5
Wariancja S^2=0
S^2=2/5
S^2=50/5
0,4
10
Odchylenie standarodwe S=pierwiastek S^2
0,6324555
3,1622777
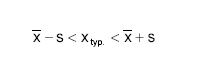

Typowy obszar zmienności
Xi *wi
Xi-Xsr
(Xi-Xsr)^2 (Xi-Xsr)^2*wi 1
0,12
2
0,2
3
0,3
4
0,22
5
0,16
Suma
1
Xi Wi*100% Xi srodek Xi *Wi*100% Xi-Xsr (Xi-Xsr)^2 (Xi-Xsr)^2*Wi*100%
4-8
5
8-12
11
12-16
15
16-20
21
20-24
34
24-28
14
Razem
Wzgledna ocena Typowego obszaru zmienności
-do porównania róznych kategorii cechy Unormowana
Unormowana
Liczba
Agent
Liczba polis liczba
liczba polis kilentów
klientów
1
64
165
2
64
167
3
65
168
4
66
173
5
67
172
6
69
176
7
69
174
8
70
181
9
70
169
10
70
175
11
71
176
12
72
171
13
72
173
14
73
178
15
73
177
Średnia
69
173
Odchylenie st 3
4
