Egzamin dla Aktuariuszy z 12 października 2002 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
X - liczba wojen w i-tej karcie i
permutacja 52
X =1 wtedy na i i 26+i to samo: i
13 – wybór figury
4
- wybór kolorów
2
2- wybór który ma która
50! – permutacja pozostałych kart
4
13
2
⋅ 5 !
0
P( X
i =
)
2
1 =
5 !
2
ODP = E(
⋅ ⋅ ⋅
⋅ ⋅
X + ... + X
=
=
=
1
26 )
13 6 2 5 !
0
26 13 12
26
26
5 !
2
51⋅ 52
17
Zadanie 2
W
( ,
2 )
2 + W 3 = X ≅ Γ
λ
W 1 = Y
∞ tx
∞
t >
Y
0
P
≤ t = P( Y ≤ tX ) = ∫ ∫ − λy 2 − λx e
λ
λ xe
dydx = ∫ 2 − λx
λ xe
( −
1 −
λtx
e
) dx =
X
0 0
0
∞
2
=
λ λt x
λ
1 − ∫ 2 −( + )
λ xe
dx = 1 −
= 1
( λ +
2
λt)
2
0
2
2
2
2 2
2 λ = λ + 2 λ t + λ t 2
2 = 1 + 2 t + t
2
t + 2 t −1 = 0
∆ = 4 − 4(− )
1 = 8
∆ = 2 2
− 2 − 2 2
t =
< 0 odpada
1
2
med = t =
= 2 −1
2
2
Zadanie 3
E( 2
2
ˆ
ˆ
θ − 2 θθ + θ ) 2
+
2
( a
k)
1
ˆ
θ
E
= E
=
a + 2 a ⋅16 θ + 16 θ 1
( − θ) + 256 θ
2
2 ( 2
2 )
( b + n)
( b + 16)
1
ˆ
Eθ =
( a + 16 θ)
b + 16
2
a + 32 aθ + 16 θ −
2
16 θ +
2
256 θ
2 aθ +
2
θ
R( θ) =
−
32
+ 2
θ =
( b +
2
16)
b + 16
2
a +
2
240
32
32
16
2
= θ
−
+
a
a
1
+ θ
−
+
2
2
2
( b + 1 )
6
b + 16
( b + 1 )
6
b + 16 ( b + 1 )
6
240 − 32( b +16) + ( b +16)2
= 0
2
( b + 16)
240 − 32 b − 512 + 2
b + 32 b + 256 = 0
→
→
32 a +16 − 2 a( b + 16)
32 a + 16 − 2 ab − 32 a =
=
0
0
( b + 16)2
2
b = 16
b = ,
4 b = 4
−
−
1
2
22
1
( 2)2
1
1
→
→
→ R =
=
, R =
=
→ n
p R =
1
2
2 ab = 16
a = ,
2 a = −2
1
2
202
100
122
36
100
Zadanie 4
var S
= E var S S + var E S S
m
( ( m n)
( ( m n)
E( S S + E X + + ...
1
+ X S = S
m
n )
( m
n
n )
n
mE( X S + ( n − m) E X S = S
i
n )
( i n) n
E(
S
m
X S
=
→ E S S =
S
i
) n
n
( m n)
n
n
n
2
var S
= σ
m
m
X
6 4
47 4
48
m
m
mσ = E var( S S +
=
+
m
n )
2
2
2
var
S
X
nσ
n
2
n
n
2
2
−
2
m
2
2
m
2
m
n
m
X = mσ −
σ = σ m
−
= σ m1
2
− = σ m
= ( E)
n
n
n
n
Zadanie 5
E( X 2 Y 2 ) = EE( X 2 Y 2 X ) = E( X 2 E( Y 2 X ) =
(
Y X )
cov( X , Y )
≅ N EY +
( x − EX ); (
2
1 − p ) 2
σ ≅ N
−
Y
( pX,( 2
1
p )
var X
= E( 2
X (1
2
2
2
− p + p X ) = (1
2
− p ) 2
2
4
EX
+ p EX = (1
2
− p )
2
+ p 3 = 2 2
p + 1
var( XY ) = 2 2
p + 1
2
− E ( XY) = 2 2
p + 1 − (cov( X , Y ) + EXEY )2 = 2 2
p + 1
2
2
− p = p +1
Zadanie 6
P( rX + 1
( − r Y
)
− d < µ < rX + 1
( − r Y
)
+ d ) = P( rX + 1(− r Y
)
− µ < d )
1
4
X ≅ N µ, , Y ≅ N µ,
4
9
25
8
4
2
= r − r+
36
9
9
6 4
4 7
4
4 8
2 1
2 4
rX + 1
( − r) Y − µ ≅ N
;
0 r
+ 1
( − r)
4
9
d
96
,
1
P X <
= 95
,
0
→ d =
25 2
r − 32 r + 16 = f ( r) → min 2
6
25 r − 32 r + 16
36
9
,
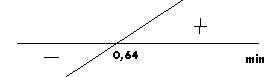
1 6 50 r − 32
32
f ′ =
= 0 → r
=
= ,
0 64
min
6
2 ...
50
9
,
1 6
d =
25 ⋅ ,
0 642 − 32 ⋅ ,
0 64 + 16 = ,
0 784
6
Zadanie 7
,...,
( )
f (
f X
X θ f θ
θ X ,..., X
1
=
1
n )
(
n
)
f ( X ,..., X
1
n )
∞
∞
n
f (
θ
X ,..., X
f X ,..., X θ f ( θ) dθ
λe λθ dθ
1
n ) = ∫
( 1
n
)
= ∫
−
θ 1
0
0 (
=
∏ xi) +
∞
λ
−
α
n
θ
n
( λ+
1
ln ∏ xi )
= +
=
∫
λ
!
n
∏
θ e
=
X
β =
n 1
λ
ln
x
x
i 0
(∏ i) =
+
∏ i ( λ + ln(∏ xi) +
n 1
+
n
+
−
∏
∏
λθ
i
i
f (
θ
X
λ
X
θ X ,..., X
=
λe
1
n )
( ln(
)
(
θ +
X
∏ i) 1
λ
!
n
n+
λθ
θ
e
( λ +
n
n
ln(∏ X
λ
X
α
n
i ) +
−
1
1
( +ln(∏ i) +1 ∞
2
θ λ ln
X
= +
n+1 − ( + (∏ i )
ODP = ∫
θ
e
θ
!
n
!
n
β
λ
ln
X
0 (
=
=
=
∏ Xi)
∫
= +
0
(∏ i)
(
1
λ + ln(∏ Xi ) n+
( n + )
1 !
n + 1
n +
=
1
n!
(
2
λ + ln(
=
=
∏
λ
ln
X
λ
ln X
X i ) n+
+ (∏ i )
+ ∑
i
Zadanie 8
Jako suma 2
χ
)
1
(
= Y, EY = ,
1 var Y = 2
2
χ ( n) − n
Z CTG
→ N( )
1
,
0
2 n
Z tego: χ 2 ( n) → N ( n,2 n) = Y
P(Y<t)=0,1
t − n
P Y
N <
= 1
,
0
2 n
t − n = − ,128
2 n
t = − ,
1 28 2 n + n
Z tego:
χ 2 ( n)
0 1
,
→ − ,
1 28 2 n + n
− ,128 2 n + n −
g =
n
lim
= − ,
1 28 2 = − 8
,
1 1
n
Zadanie 9
1
θ 10
2
2 (∏ X i ) θ −
L =
2
1
1
θ 10
1
1 (
X )
θ > θ → STAT =
−
∏
∏
X i
θ
i
P
0 (∏ X
ln
ln
i > t ) = P 0 (∑
X i >
t )
t
P(
e
t
ln X
t
P X
e
x
θ
1
x
e t
(
0
; )
i <
) = ( < t
i
)= ∫ θ− = [ ] eθ 0 = t ∈ −∞
0
= − X X ≅ wykl( θ)
≅ χ(20)
6 4
4 7
4
4 8
−ln t
−ln t
− t
1
1
P (
ln )
(
ln )
2 ln
,
8 26
0 − Y >
t = P Y
0
< − t = ∫
9 − x
x e dx =
= t
x
= ∫
t 9 e 2 → −
t =
10
!
9
2
2 Γ 1
(
)
0
0
0
4 1
, 3
10
4 1
, 3 θ
8,26 θ
moc = ∫ θ
9 − x
θ
x e
= ∫ 1 9 − x
x e dx =
= t
x
= ∫ 2
χ (20) ≥ 9
,
0 9 →
!
9
!
9
2
0
0
0
→ 37 5
, 66 ≤ ,
8 26 θ → θ ≥
5
,
4 5
9
∑ P(> 6 i) P( i) i=1
8
1
P )
1
(
= 1 przejdzie od 2 do 10
3
7
2
1
P(2) =
3
3
6
2 1
P )
3
(
=
3 3
....
2 1
P )
8
(
=
3 3
2
P 9
( ) =
3
18
i = 1
P( i) = 3
10− i−
1
2 1
i ∈[ 9
;
2 ]
3 3
8
2
7
6
5
4
3
2
2 1
2
1
1
1
1
1
2 1
1
80
ODP =
+ + + + +
+
+ +1 =
3 3
3
3
3
3
3
3
3 3
3
81