







1. Wprowadzenie
Fale rozchodzące się przestrzeni, które docierają do naszych uszu wywołują wrażenie dźwięku. Są to fale o częstotliwości od 16 do 20 000 Hz.
Prędkość propagacji fali zależy od właściwości mechanicznych ośrodka.
Rozchodzenia się w gazie fala dźwiękowa jest falą podłużną polegającą na przemieszczaniu się jego zagęszczeń i rozrzedzeń. Ze względu na dużą prędkość rozchodzenia się fali możemy przyjąć, że mamy do czynienia z procesami adiabatycznymi, a wówczas otrzymujemy wzór na jej prędkość w postaci:
gdzie
jest stosunkiem ciepła właściwego przy stałym ciśnieniu do ciepła właściwego przy stałej objętości, p- ciśnienie, ρ- gęstością gazu. Uwzględniając, że zależność gęstości gazu od temperatury dana jest wyrażeniem:
gdzie jest gęstością w t = 0ºC, współczynnikiem rozszerzalności gazu, t temperatura w skali Celsjusza, otrzymujemy: gdzie to prędkość rozchodzenia się dźwięku w powietrzu w temperaturze 0ºC, bez względu na jego ciśnienie. W suchym powietrzu
2. Metoda pomiaru
Akustyczne fale stojące można wzbudzić w słupie powietrza. Jeżeli jeden koniec rury jest zamknięty, to fale wzbudzone u wylotu rury rozchodzą się w powietrzu i odbijają na jej końcu. Fala stojąca powstaje w wyniku super pozycji fal padających i odbitych. Jeżeli długość półotwartej rury spełnia warunek:
gdzie n = 0, 1, 2, 3...
to na zamkniętym końcu rury powstaje węzeł, a na końcu otwartym strzałką fali stojącej.
Amplituda drgań u wlotu rury osiąga maksymalną wartość i jednocześnie obserwuje się silne wzmocnienie dźwięku.
Pomiar długości słupa powietrza, w którym powstaje fala stojąca, jeśli znamy częstotliwość źródła wymuszającego drgania, pozwala wyznaczyć długość fali λ oraz prędkość dźwięku V = λf.
Lp
połorzenie x1 [cm] połorzenie x2 [cm]
1
15,4
53,3
2
15,5
53,4
3
15,1
53,6
4
15,4
53,3
5
15,3
53,6
x 1= 15,34 [cm]
x 2= 53,44 [cm]
f = 453,32 Hz
t = 25 oC
α=(1/273,15 °C)
- Obliczanie niepewności systematycznej:
∆sx = 0,05 [cm] = 0,0005 [m]
-
Obliczanie rozrzutu wartości x1 i x2:
x1max – x1min = 0,4 [cm] = 0,004 [m]
x2max – x2min = 0,3 [cm] = 0,003 [m]
rozrzut wartości jest znacznie większy od niepewności systematycznej, więc możemy pominąć niepewność systematyczną:
x1max – x1min >> ∆sx
x2max – x2min >> ∆sx
- Obliczanie niepewności przypadkowej (odchylenie standardowe średniej arytmetycznej):
S x 1= 0,068
S x 2= 0,068
ilość pomiarów jest mniejsza od dziesięciu, a więc odchylenie standardowe średniej arytmetycznej S x daje zaniżoną wartość niepewności systematycznej.
τ nα= 4,60 , gdzie n= 5, a α=0,99
∆cx1= S x . τ nα= 0,31
∆cx2= S x . τ nα= 0,31
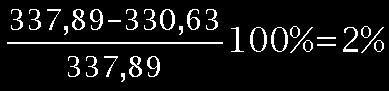
- Obliczanie długości fali w powietrzu:
λ = 2( x 2 - x 1) ≈ 76,2 [cm] = 0,762 [m]
- Obliczanie prędkość dźwięku w temperaturze pokojowej:
V = λ . f ≈ 345,43
- Obliczanie prędkości dźwięku w temperaturze 0°C
V0 = V / ( 1 + α t ) ≈ 330,63 [m/s]
- Obliczanie maksymalnej niepewności pomiaru:
∆V= 7,26 [m/s]
- Prędkość dźwięku w powietrzu w temperaturze 0°C:
V = ( 330,63 ± 7,26 ) [m/s]
V%=
4. Wnioski:
Wyniki prowadzonych obliczeń różnią się od wartości przedstawionych w tablicach , czego powodem są błędy pomiarowe i nie uwzględnienie wszystkich czynników jakie miały wpływ na dokładność pomiarów. Największy wpływ na obliczanie wartości V miał z pewnością pomiar związany z badaniem wysokości słupa powietrza w rurze.
Wyszukiwarka
Podobne podstrony:
ćw. 29 sprawozdanie II
ćw 29 sprawozdanie III
ETX16 20061012 Ćw[1] 29 sprawozdanie
cw.29-sprawozdanie, Studia zaoczne PWR, semestr 3, regresja
ćw 29
sily hamowania(2), SiMR, Pojazdy, Laboratorium Pojazdów, ćw.1 hamulce, Sprawozdanie
Cw 29 szablon id 97632 Nieznany
Fizyka laboratorium ćw 75 (SPRAWOZDANIE)
ćw 14 sprawozdanie I
29 sprawozdanie
ĆW 77- SPRAWOZDANIE, Automatyka i robotyka air pwr, III SEMESTR, FIZYKA 2, sprawko 77
ćw.29, 29
cw 3 nadwyzki sprawozdanie nadwyżki dynamiczne moje
51, F CW 51, Sprawozdanie z ?w. nr 51
51, F CW 51, Sprawozdanie z ?w. nr 51
29 sprawozdanie
ćw 16 sprawozdanie I
więcej podobnych podstron

