Współrzędne elipsoidalne
Przeliczanie współrzędnych ortokartezjańskich na elipsoidalne i odwrotnie.
Zamiana współrzędnych geodezyjnych na ortokartezjańskie to inaczej redukcja współrzędnych geodezyjnych na powierzchnię odniesienia. Tego typu redukcję moŜna wykonać róŜnymi metodami. Proces redukcji ma wprowadzać jak najmniejsze zniekształcenia do wielkości pomierzonych, tzn. do współrzędnych (x, y, z) wyznaczonych techniką GPS.
Mamy do wyboru cztery róŜne metody redukcji współrzędnych na powierzchnię elipsoidy odniesienia:
• Helmerta – bezpośrednio wzdłuŜ normalnych do elipsoidy
• Pizzettiego – w rzeczywistym polu siły cięŜkości
• w normalnym polu siły cięŜkości
• redukcję za pomocą geometrycznych linii pionu 1. Metoda Helmerta bezpośredniego rzutowania na elipsoidę.
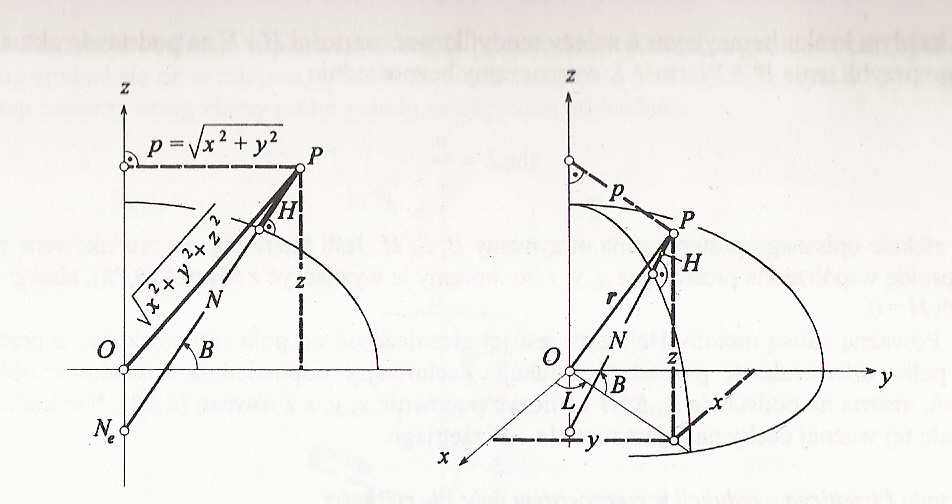
Rys. 1 Zamiana współrzędnych prostokątnych x, y, z na B, L, H; redukcja na elipsoidę metodą Helmerta.
Metoda ta wywodzi się ze wzorów: x = ( N + H )cos B cos L
y = ( N + H )cos B sin L
z = ( 1
τ− N + H ) 1
-
2
sin B
gdzie :
τ =1 − e
Na podstawie tych równań moŜna napisać następujące związki dla odległości punktu o współrzędnych x, y, z od osi Oz:
p = x 2 + y 2 = ( N + H )cos B
a następnie dla wysokości ponad elipsoidą p
H =
− N
cos B
1
Współrzędne elipsoidalne Promień krzywizny przekroju elipsoidy w pierwszym wertykale wyraŜa wzór: a
N =
1 − e 2
2
sin B
Po podzieleniu równania na z przez p otrzymamy równanie iteracyjne o następującej postaci: ( k )
−1
(
z
N
k 1
+ )
2
tan B
=
1
− e
(
k )
( k )
p
N
+ H
przy czym
( =
z
1
0 )
tan B k
=
2
p 1 − e
W kaŜdym kroku iteracyjnym k naleŜy modyfikować wartość H i N na podstawie aktualnego przybliŜenia B(k).
Wartość L wyznaczamy bezpośrednio: y
tan L =
x
W efekcie opisanego postępowania otrzymamy B, L i H. Jeśli interesują nas współrzędne zredukowane na elipsoidę x, y, z to moŜemy je wyznaczyć z równań wyjściowych podstawiając H=0. Metoda ta jest niezaleŜna od pola cięŜkości.
2