Wykład 1
PROJEKTOWANIE PROSTEGO SERWOMECHANIZMU
1.1. Serwomechanizm prądu stałego
1.2. Opis i bloki elementów układu
1.3. Schemat blokowy i transmitancja układu 1.4. Projektowanie – dobór nastaw
1.5. Symulacja – Matlab
1.1. Serwomechanizm prądu stałego
Serwomechanizm jest układem stabilizacji położenia silnika (elektrycznego, hydraulicznego, pneumatycznego). W przypadku silnika elektrycznego steruje się kątem obrotu lub liczbą obrotów.
Zastosowanie: obrabiarki (3D), suwnice, podajniki, roboty (5D, 6D), stacje radarowe, itp.
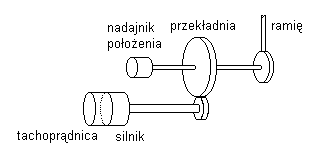
• Mechanika serwomechanizmu
• Realizacja nadajnika położenia:
- potencjometr
wieloobrotowy
-
rezolwer (maszyna elektryczna, rodzaj selsynu)
-
enkoder (karta kodowa + licznik foto elektryczny)
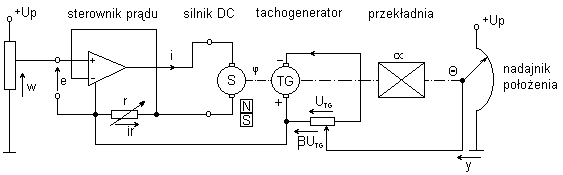
• Schemat elektryczny serwomechanizmu Rys. 1.1. Schemat elektryczny układu prądowego sterowania silnikiem
• Problem sterowania
Jakie wartości r, β należy ustawić, aby przebiegi regulacyjne były aperiodyczne krytyczne o stałej czasowej T=0.2 s ?
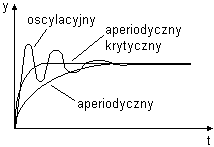
Typowe przebiegi wielkości regulowanych
-
przebieg oscylacyjny
– pierwiastki zespolone
-
przebieg aperiodyczny krytyczny
– pierwiastki rzeczywiste wielokrotne
-
przebieg aperiodyczny
– pierwiastki rzeczywiste jednokrotne
1.2. Opis i schematy blokowe elementów układu
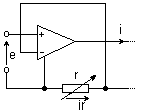
• Sterownik prądu
U + − U− ≅ 0
e − ir ≅ 0
e
i
1
i
1
≅ e
r
r
• Silnik prądu stałego
Dane:
MemN = 20 Nm
iN = 10 A
J = 0.0005 kg m2 (moment bezwładności wirnika i przekładni) Równanie momentów
dω
J
= M
M
M
em −
,
o
o ≅ 0
dt
20
Nm
M
k
2
s =
=
em = ksi – moment proporcjonalny do prądu
10
A
dω
J
= k i
dt
s
k
JsΩ( s) = k I ( s) ⇒
(
Ω s)
s
=
I ( s)
s
Js
Położenie – kąt φ
= ω
dt
1
sΦ( s) = Ω( s) ⇒ Φ( s) = Ω( s) s
Mo
i
-
M
em
1
ω
1
φ
ks Js s Rys.1.2. Silnik sterowany prądowo – schemat blokowy
• Przekładnia
α = 0.01
φ
θ
α
• Nadajnik położenia (potencjometr)
ΘM – maksymalny kąt obrotu, np. 5 obrotów
– zakres wejścia
ΘM = 5 2π [rd]
Up = 12 V – napięcie polaryzacji
– zakres wyjścia
U
y
θ
p
Θ
M
Proporcja:
Θ ⇒ y
Up
Θ ⇒
y =
U
U
Θ
= Θ y , stąd
Θ
M
p
p
M
Θ M
Współczynnik przeliczeniowy oblicza się jako „zakres WY – przez –zakres WE”
• Tachogenerator
n
N = 12 000 [obr / min]
U
TGN = 10 V
2π
ω
N = 12 000
[rd/s]
60
UTGN
−3
ω
U
k
=
= 7.95⋅10
TG
[V/rd/s]
TG
ω
kTG
N
" zakres − przez −
"
zakres
• Potencjometr tachogeneratora
UTG
βU
T
β
• Sumator
e = w – y − βUTG
y – wyjście układu (zmienna procesowa)
Rolę sumatora w przemysłowym układzie pełni procesor.
1.3. Schemat blokowy i transmitancja układu
1) Schemat wyjściowy
M0=0
Mem
w
e
i
ω
φ
1
θ
k
1
1
U p
α
y
– – r
s Js s Θ
M
y
β kTG
sprzężenie tachometryczne
sprzężenie pozycyjne
2) Schemat uproszczony
w
e
y
1
k α
s U p
– – 2
s
rJΘ
M
y
sβ
Θ
TG
k
M
2
U
α
ω
p
N
ξ
2
ω N
Rys.1.3. Schemat blokowy układu sterowania
• Wyznaczanie transmitancji
1
Y
2
=
ω E
s 2
N
ξ
E = W − Y − β U
β
2
U
= s
TG ,
Y
TG
ω
N
ω2
ξ
2
Y = N 2 W − Y −
sY
s
ω N
Ys 2 + 2ξω sY
2
+ ω Y
2
= ω W
N
N
N
2
ω
ξ – współczynnik tłumienia Y ( s)
N
=
W ( s)
2
s + 2
2
ξω s +ω
ω N – częstotliwość naturalna
N
N
1.4. Projektowanie – dobór nastaw
Wymagania:
a) przebiegi aperiodyczne krytyczne
b) stała czasowa 0.2
Ad. a) ∆ = 0 – pierwiastki rzeczywiste podwójne
∆ < 0 – pierwiastki zespolone (oscylacyjne)
∆ > 0 – pierwiastki rzeczywiste różne (aperiodyczne zwykłe) Serwomechanizmy nastawia się na przebiegi aperiodyczne krytyczne.
• ∆ = 0:
∆ = 4 2 2
ξ ω
,
⇒
ξ =
N − 4
2
ω N = 4 2
ω ( 2
N ξ
− )
1 = 0
1
• Tzam = 0.2
2
ω
2
ω
ξ
1
1
= 1 :
N
N
=
=
⇒
= Tzam = 0 2
.
2
2
s + 2ξω s + ω
2
( s + ω )
1
ω
N
N
N
(
s + 2
)
1
N
ω N
ω
N = 5
Wniosek. Z warunków ξ = 1, ω N = 5 wyznaczymy dwie niewiadome r, β.
• Obliczenia
2ξ
2 ⋅1
β kTGΘ
2
01
.
0
M
⋅12
=
=
⇒ β = ⋅
= 192
.
0
ω
5
U
N
α
5
95
.
7
p
⋅10−3 ⋅10π
Potencjometr ustawiamy na 19.2 %
kSα U p
⋅
⋅
2
2
01
.
0
12
ω N = 25 =
⇒ r =
= .
0 61
Θ
rJ
25
M
⋅ 0005
.
0
⋅10π
Rezystor w sprzężeniu sterownika prądu
1.5. Symulacja – Matlab
k
U
α
2ξ
β k Θ
S
p
28
.
15
ω =
=
2
2
2
2
TG
M
ξω =
⋅ω =
ω = β ⋅ 08
.
2
⋅ω
N
,
rJΘ
r
N
N
N
N
ω
α U
M
N
p
• Według projektu
Matlab
beta = 0.192
r = 0.61
omn = sqrt(15.28/r)
dwaksiomn = beta*2.08*omn^2
l = omn^2
m = [1 dwaksiomn omn^2]
t = 0:0.05:5
y = step(l,m,t)
plot(t,y), grid
Rys.1.4. Przebieg aperiodyczny krytyczny
• Odłączenie tachogeneratora
Matlab
beta = 0
r = 0.61
omn = sqrt(15.28/r)
dwaksiomn = beta*2.08*omn^2
l = omn^2
m = [1 dwaksiomn omn^2]
t = 0:0.05:5
y1 = step(l,m,t)
plot(t,y,t,y1), grid
Rys. 1.5. Przebieg oscylacyjny
Odłączenie tachogeneratora powoduje pojawienie się oscylacji – układ nie nadaje się do pracy.
• Przypadkowe nastawy
Matlab
beta = 0.5 – potencjometr na 50%
r = 1 – mały rezystor w sprzężeniu zwrotnym omn = sqrt(15.28/r)
dwaksiomn = beta*2.08*omn^2
l = omn^2
m = [1 dwaksiomn omn^2]
t = 0:0.05:5
y2 = step(l,m,t)
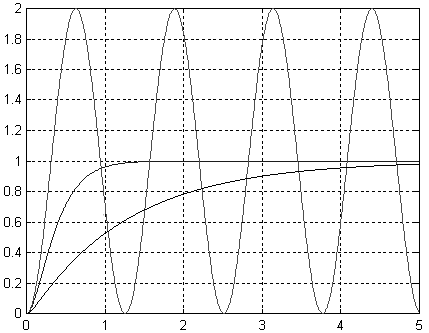
plot(t,y,t,y1,’r’,t,y2,’k’), grid
Rys. 1.6. Przebiegi: oscylacyjny, aperiodyczny krytyczny i aperiodyczny zwykły.
Przy przebiegach aperiodycznych zwykłych serwomechanizm ma wyraźnie dłuższy czas regulacji.