Ważniejsze daty:
1833-Faraday zaobserwował zmniejszenie oporu siarczku srebra podczas
ogrzewania
1875- W. Simens –komórka fotoelektryczna- pierwszy przyrząd półprzewodnikowy
1883-C.E. Frits –prostownik selenowy.
1906-detektor krystaliczny-złącze metal półprzewodnik (PbS)
1913-W. L. Bragg- określenie struktury kryształów KCl, NaCl, KBr, KJ (Nobel 1915)
1914-Dioda Schotky’ego
1918-J. Czochralski-metoda wzrostu monokryształów
1947-L. Sosnowski-teoria złącz p-n
1948-J.Bardeen, W.H. Brattain , W.B. Shockley tranzystor (Nobel 1956)
1955-J. Luttinger, W. Kohn –formalizm masy efektywnej
1959-J. S. Kilby – układ scalony (Nobel 2000)
1963- Z. I. Alferov, H. Kromer –złącze p-n ze studnią kwantową
1969- L. Esaki, R. Tsu – supersieci
1980-K. von Klitzing –Kwantowy Efekt Halla (Nobel 1985)
1982-D.C. Tsui, H.L. Stormer, R.B. Lunghlin -ułamkowy kwantowy efekt Halla.
Faza skondensowana
Do fazy skondensowanej zaliczają się ciała stałe oraz ciecze. W gazach atomy lub
cząsteczki (molekuły) w wyniku wzajemnych zderzeń wykonują przypadkowe ruchy
translacyjne, oraz molekuły wykonują ruchy rotacyjne i oscylacyjne. W cieczach ruch
postępowy jest ograniczony w porównaniu z gazami i większość czasu cząsteczki
znajdują się w ruchu rotacyjnym i oscylacyjnym (rys.1.1b). W ciałach stałych ruch
cząsteczki sprowadza się głównie do małych drgań około jej położenia równowagi
oraz rotacji molekuł dookoła ich osi symetrii (rys.1.1c). Postępowe ruchy cząsteczek
w ciele stałym są bardzo rzadkie. Oprócz różnicy w zachowaniu cząsteczek w fazie
skondensowanej i fazie gazowej, w fazie skondensowanej wzajemne odległości
cząsteczek są rzędu ich średnicy (w gazach ta odległość jest na porządek większa),
a siły oddziaływania między cząstkami powodują, że ciało w fazie skondensowanej
ma określoną gęstość ρ i zajmuje określoną objętość V .Natomiast gaz zajmuje całą
objętość naczynia, w którym został umieszczony.
Rys.1.1. Trajektorie cząsteczek w gazie (a), cieczy (b) i ciele stałym (c)
Ciała w fazie skondensowanej można podzielić na pięć różnych typów:
1. ciecze;
2. szkła;
3. ciała amorficzne;
4. kryształy,
5. ciekłe kryształy.
• Ciecze są to równowagowe, izotropowe, nieuporządkowane przestrzennie ciała
przyjmujące kształt naczynia, w jakim się znajdują. Ciecze, podobnie jak ciała stałe,
są mało ściśliwe. Ta własność cieczy jest związana z dość silnymi oddziaływaniami
między cząstkami. Każda substancja ciekła (z wyjątkiem helu) podczas oziębiania
traci swoje własności ciekłe i przechodzi w ciało stałe.
• Szkła są to kwazirównowagowe (kwazi od łacińskiego słowa quasi, które w
połączeniu z innymi wyrazami oznacza: jak gdyby, jakoby, rzekomo), izotropowe,
nieuporządkowane przestrzennie ciała stałe posiadające właściwości sprężyste ciał
stałych. Wskutek tego w szkle mogą rozchodzić się tak podłużne, jak i poprzeczne
fale dźwiękowe. W gazach i cieczach mogą rozchodzić się tylko fale podłużne.
Substancje szkło-podobne samorzutnie powoli przekształcają się w postać
równowagową -krystaliczną. Z tego właśnie powodu stan w którym znajduje się szkło
nazywa się stanem kwazirównowagowym.
• Ciała amorficzne, jak i ciała szkliste, są izotropowe, nieuporządkowane
przestrzennie ciała stałe posiadające właściwości sprężyste ciał stałych. Jednak, w
odróżnieniu od szkieł, stan ciał amorficznych jest równowagowy i ciała amorficzne
nigdy nie przekształcają się w stan krystaliczny. Amorficzne ciała są w istocie
cieczami przechłodzonymi i przykładami takich ciał są lak, wosk, smoła i inne.
Amorficzne jak i szkliste substancje powstają wskutek szybkiego wzrostu ich lepkości
przy obniżaniu temperatury substancji. To powoduje, że ruch cząsteczek konieczny
do uformowania się i wzrostu kryształu jest utrudniony i substancja zestala się
wcześniej niż nastąpi krystalizacja.
Rys.1.2. Uporządkowanie dalekiego (z lewej strony) i bliskiego zasięgu (z prawej
strony)
• Kryształy są to równowagowe, anizotropowe, uporządkowane przestrzennie ciała
stałe. Kryształy powstają wskutek procesu, który nosi nazwę krystalizacji. Ten proces
polega na tym, że w cieczy, oziębionej do określonej temperatury, pojawiają się tzw.
centra krystalizacji - drobne kryształki, czyli obszary uporządkowanych i trwale
związanych ze sobą cząstek. W warunkach umożliwiających swobodny wzrost, przy
dalszym oziębianiu cieczy centra krystalizacji rozrastają się w kryształy, tj. w
trójwymiarowe okresowe ułożenia atomów, lub grup atomów. Cząstki (atomy, jony
lub molekuły), z których zbudowany jest kryształ rozmieszczone są w przestrzeni
okresowo, tworząc sieć krystaliczną (rys.1.2). Mówimy, że w krysztale istnieje
uporządkowanie dalekiego zasięgu.
W cieczach i amorficznych substancjach, w odróżnieniu od kryształów nie istnieje
uporządkowanie dalekiego zasięgu. Jednak badania rozpraszania promieni
rentgenowskich na tych bezpostaciowych substancjach wskazują na to, że tutaj też
można zauważyć porządek. A mianowicie, w sferze otaczającej pewną wybraną
cząstkę o promieniu rzędu 3÷4 średnic cząstki, wzajemne ułożenie sąsiadujących
cząstek jest podobne do uporządkowanego ułożenia sąsiadujących cząstek w
kryształach (rys.1.2). Tego typu uporządkowanie nosi nazwę uporządkowania
bliskiego zasięgu.
• Ciekły kryształy są to równowagowe, anizotropowe, częściowo uporządkowane
substancje. Ze względu na anizotropię fizycznych właściwości, ciekły kryształy
podobne do zwykłych kryształów. Jednak ze względu na małą lepkość oraz łatwość
deformacji ciekłe kryształy są zbliżone do cieczy. Ciekłe kryształy są zbudowane z
drobin, które posiadają kształt albo długich „cygar”, albo dużych „naleśników”. W
ciekłych kryształach istnieje uporządkowanie długiego zasięgu ale tylko w jednym
albo w dwóch wymiarach.
Klasyfikacja ciał stałych względem ich właściwości fizycznych
W tej klasyfikacji ciał stałych jako kryterium występuje jedna z właściwości
fizycznych: mechaniczna; elektryczna; magnetyczna; termiczna albo optyczna.
Fizyczne właściwości ciał stałych mają ścisły związek z wewnętrzną budową ciała
stałego.
Ze względu na właściwości mechaniczne ciała stałe różnią się odpornością na
mechaniczne działania z zewnątrz typu uderzenia, zginania lub nacisku. Rozróżniają
ciała stałe:
• twarde (diament, korund –Al203),
• kruche (szkło, kwarc),
• ciągliwe (miedź),
• plastyczne
• kowalne (metale),
• sprężyste,
• łupliwe (właściwość tylko kryształów) itd.
Ze względu na właściwości elektryczne ciała stałe dzielimy na:
• dielektryki,
• półprzewodniki,
• przewodniki
• nadprzewodniki.
Dielektryki to są ciała stałe które nie posiadają swobodnych elektronów a zatem są
złymi przewodnikami prądu elektrycznego. Spośród dielektryków osobno wyróżniają:
• piroelektryki,
• ferroelektryki
• piezoelektryki.
Piroelektryki są to kryształy które posiadają niezerową polaryzację elektryczną
r
(makroskopowy moment dipolowy P ) nawet w zerowym polu elektrycznym. Zmiany
r
temperatury kryształu powodują zmianę polaryzacji a zmiana
P
∆ jest wprost
proporcjonalna do zmiany temperatury:
r
r
P
∆ = P T
∆ (0.1)
Efekt określony przez wzór (0.1) nazywa się efektem piroelektrycznym, a składowe
r
wektora P w (0.1) noszą nazwę współczynników efektu piroelektrycznego.
Ferroelektryki są to substancje, które jak i piroelektryki wykazują samoistną
(spontaniczną) polaryzację elektryczną poniżej określonej temperatury (temperatury
Curie T ). Jednak w odróżnieniu od piroelektryków, możemy zawsze odwrócić
C
r
kierunek wektora polaryzacji spontanicznej P stosując zewnętrzne pole elektryczne.
Powyżej temperatury Curie ciało stałe przestaje być ferooelektrykiem i przechodzi w
stan który nazywamy stanem paraelektrycznym. W nieobecności zewnętrznego pola
elektrycznego poniżej T cała objętość ferroelektryka spontanicznie dzieli się na
C
r
małe spolaryzowane obszary o swojej polaryzacji elektrycznej P .. Takie małe
i
r
spolaryzowane obszary nazywają się domenami. Dopuszczalne kierunki wektorów P
w domenach określa symetria kryształu. Jednak w zerowym zewnętrznym polu
r
r
elektrycznym suma wszystkich P jest zawsze równa zeru ∑ P
i = 0
i
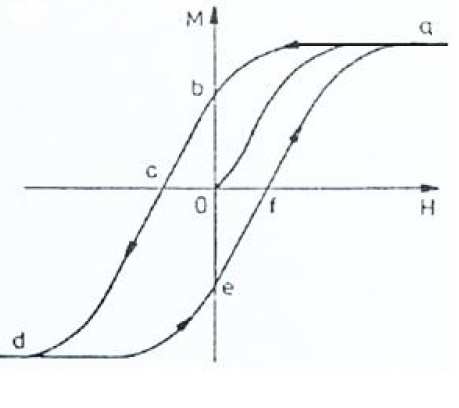
Rys.1.3. Pętla histerezy
Zależność polaryzacji kryształu od natężenia zewnętrznego pola elektrycznego jest
przedstawiona na rys.1.3. Ma ona kształt pętli nazywanej pętlą histerezy. Przyłożone
zewnętrzne pole elektryczne powoduje, że ze wzrostem natężenia pola
r
elektrycznego E zaczyna rosnąć polaryzacja początkowo niespolaryzowanego
r
kryształu do maksymalnej wartości P
(punkt a na rys.1.3). Wzrost polaryzacji
Max
kryształu zachodzi w wyniku zmiany granic między domenami, wskutek czego rośnie
r r
r
objętość domen z P E . Maksymalna wartość polaryzacji P
odpowiada stanowi
Max
nasycenia. W tym stanie w krysztale znikają wszystkie domeny z polaryzacją
r
r r
nierównoległą do E a domeny z P E zajmują całą objętość kryształu. Jeżeli teraz
zaczniemy zmniejszać natężenie pola elektrycznego, to polaryzacja kryształu
r
zaczyna maleć (rys.1.3). Jednak przy E = 0 polaryzacja nie staje się równa zeru, a
r
osiąga wartość P , która nosi nazwę polaryzacji szczątkowej. Polaryzacja znika
s
całkowicie tylko pod wpływem przeciwnie skierowanego pola elektrycznego o
r
r
natężeniu − E . Wartość natężenia − E nazywa się polem koercji
c
c
Piezoelektryki są to kryształy, w których występuję efekt piezoelektryczny.
Rozróżniamy efekt piezoelektryczny prosty i odwrotny. Efekt piezoelektryczny prosty
obejmuje zjawiska polegające na tym, że w pewnych kryształach naprężenia
mechaniczne albo deformacje powodują wystąpienie w nich polaryzacji elektrycznej
albo pola elektrycznego, które jest wprost proporcjonalne do wielkości przyłożonego
naprężenia albo deformacji. Natomiast efekt piezoelektryczny odwrotny, jak wynika z
nazwy efektu, obejmuje grupę zjawisk polegających na tym, że kryształ pod wpływem
zewnętrznego pola elektrycznego albo zmiany polaryzacji elektrycznej kryształu
deformuje się i zmienia swój kształt.
Ze względu na właściwości magnetyczne ciała stałe dzielimy na
• paramagnetyki
• ciała uporządkowane magnetycznie ( magnetyki).
Diamagnetyki są to substancje, które w zewnętrznym polu magnetycznym o indukcji
r
r
r
B uzyskują indukowane namagnesowanie J skierowane przeciwnie do B Innymi
słowy podatność magnetyczna diamagnetyków jest ujemna. Diamagnetyki są
odpychane przez magnes. Własności diamagnetyczne posiadają substancje
zbudowane z atomów (cząsteczek) o zerowym wypadkowym momencie
magnetycznym.
Paramagnetyki są to substancje, które w zewnętrznym polu magnetycznym o indukcji
r
r
B uzyskują indukowane namagnesowanie J skierowane wzdłuż B
Innymi słowy podatność magnetyczna paramagnetyków jest dodatnia. Do
paramagnetyków należą substancje, w których atomy (cząsteczki) mają niezerowe
momenty magnetyczne. Gdy brak zewnętrznego pola magnetycznego, momenty
magnetyczne cząsteczek są zorientowane chaotyczne, tak że wypadkowe
namagnesowanie substancji jest zerowe. W zewnętrznym polu magnetycznym
r
B każdy z momentów magnetycznych zaczyna wykonywać precesję Larmora
r
dookoła wektora B , wskutek czego substancja uzyskuje namagnesowanie
r
r
J skierowane równolegle do B . Paramagnetyki są przyciągane przez magnes.
Magnetyki
są
to
substancje
które
wykazują
samoistne
(spontaniczne)
namagnesowanie
niżej określonej temperatury (temperatury Curie T ) nawet w nieobecności
C
zewnętrznego pola magnetycznego. Temperatura Curie oddziela nieuporządkowaną
fazę paramagnetyczną (przy T > TC ) od uporządkowanej magnetycznie fazy (przy
T < T ). Magnetyki wykazują dużą podatność magnetyczną i są podzielone na
C
ferromagnetyki, antyferromagnetyki i ferrimagnetyki (rys.1.4).W ferromagnetykach
wszystkie momenty magnetyczne atomów są uporządkowane w jednym kierunku. W
ferromagnetykach, podobnie do ferroelektryków, w zerowym zewnętrznym polu
r
magnetycznym powstają domeny o swoim namagnesowaniu J a zależność
i
r
r
r
J = ∑ J od indukcji zewnętrznego pola magnetycznego B ma charakter pętli
i
histerezy (rys.1.3).Rys.1.4. Różne typy uporządkowania magnetycznego W
domenach antyferromagnetyków część momentów magnetycznych cząsteczek jest
r
uporządkowana w jednym kierunku i tworzy wypadkowe namagnesowanie J , zaś
inna część jest uporządkowana w przeciwnym kierunku i wypadkowe
namagnesowanie tych cząsteczek wynosi ↓ ↑ J = − J (rys.1.4).
W ferrimagnetykach, tak samo jak w antyferromagnetykach, mamy dwie (a czasami
kilka) „podsieci” uporządkowanych momentów magnetycznych, jednak tutaj ↓ ↑ J ≠ − J
(rys.1.4).
Ze względu na właściwości optyczne ciała stałe są różne względem barwy, połysku,
widma absorpcji i emisji światła. W niektórych kryształach obserwuje się zjawisko
podwójnego załamania światła, polegające na tym, że padający na kryształ promień
świetlny rozszczepia się na dwa promienie, które rozchodzą się w krysztale w
różnych kierunkach z różnymi prędkościami. Ciała stałe różnią się względem zmian
swoich właściwości optycznych w zewnętrznym polu elektrycznym (efekt
elektrooptyczny) oraz pod wpływem przyłożonego z zewnątrz naprężenia
mechanicznego (efekt elastooptyczny).
Promieniowanie termiczne ciał. Prawo Kirchoffa.
Promieniowanie termiczne ciał w myśl klasycznej elektrodynamiki powstaje w
wyniku przyspieszeń, jakich doznają ładunki elektryczne w cząsteczkach w następstwie ruchu
cieplnego. Zgodnie z prawami elektrodynamiki klasycznej każdy ładunek, który posiada
różne od zera przyspieszenie, wypromieniowuje falę elektromagnetyczną. Można zatem
krótko stwierdzić, że promieniowanie cieplne jest to promieniowanie elektromagnetyczne
atomów i cząsteczek powstające kosztem ich ruchu cieplnego. Z przedstawionego określenia
wynika, że promieniuje każde ciało, o temperaturze większej od zera bezwzględnego. Należy
zauważyć, nie wnikając na razie w uzasadnienie tego stwierdzenia, że długości fal
emitowanego promieniowania cieplnego zależą od budowy atomów i cząsteczek oraz
struktury ciała. W przypadku ciał stałych i cieczy widmo promieniowania jest ciągłe i
obejmuje szeroki zakres długości fal. Przy wzroście temperatury ciała wartości emitowanych
długości fal przesuwają w kierunku fal krótszych i po przekroczeniu ok. 500C (773K) widmo
promieniowania cieplnego zaczyna być widzialne - osiąga zakres światła widzialnego. Część
promieniowania cieplnego staje się wtedy widzialna.
Ciało emituje promieniowanie cieplne kosztem doprowadzonego z zewnątrz ciepła lub
kosztem energii wewnętrznej ciała. Jeżeli promieniowanie to pada na inne ciało, wówczas w
wyniku oddziaływania pola elekromagnetycznego fali z elektrycznymi ładunkami substancji
część energii unoszonej przez falę ulegnie absorpcji, przechodząc w końcowym efekcie
powtórnie w energię ruchu cieplnego. Jest więc promieniowanie cieplne obok konwekcji i
przewodnictwa cieplnego, jedną z form wymiany ciepła. Ta forma wymiany ciepła,
odbywająca się za pośrednictwem fal elektromagnetycznych wyróżnia się tym, że może
zachodzić również w próżni.
Własności emisyjne ciała charakteryzuje wielkość
M , zwana emitancją
T
promieniowania. Określa ją związek
dW
M =
, (1.1)
T
dS
gdzie W odpowiada mocy wypromieniowanej energii dS jest elementem powierzchni ciała
promieniującego. Można zatem określić emitancję jako wielkość liczbową równą
strumieniowi promieniowania (moc z jednostki powierzchni). Jednostką emitancji w układzie
SI jest W/m2 . Za pomocą elementu rozszczepiającego światło w postaci siatki dyfrakcyjnej
lub pryzmatu z materiału przepuszczającego promieniowanie cieplne (np. z monokryształów
NaCl lub LiF) można otrzymać widmo promieniowania cieplnego. Umieszczając z kolei w
różnych
częściach
widma
detektor
promieniowania
można
zmierzyć
emitancję
promieniowania dM w wąskich przedziałach długości fal od λ do λ + dλ .Wielkość
T
wyrażoną stosunkiem:
dM
M
T
=
,
λ
(1.2)
T
dλ
Nazywamy spektralną (widmową) emitancją promieniowania lub spektralną gęstością
emitancji lub funkcją rozkładu widmowego promieniowania danego ciała. Emitancja
spektralna M λ jest zatem liczbowo równa strumieniowi promieniowania w jednostkowym
T
przedziale długości fali w pobliżu długości λ . Oczywiście emitancję promieniowania
M zwaną często całkowitą emitancją, otrzymamy całkując emitancję spektralną po
T
wszystkich długościach fal:
∞
M = ∫ M
(1.3)
T
λ T λ
d
0
Własności absorpcyjne ciała charakteryzuje spektralny czyli widmowy współczynnik
pochłaniania (absorpcji) αλ . Jest to bezwymiarowa liczba określająca jaka część padającego
T
na ciało promieniowania o długości fali od λ do λ + dλ ulega absorpcji. Oczywiście
α
. Podobnie jak emitancja spektralna tak i spektralny współczynnik absorpcji zależy od
T
λ ≤ 1
rodzaju ciała, stanu jego powierzchni, temperatury oraz długości fali promieniowania.
Charakterystyczne dla różnych ciał różnice wartości w różnych częściach widma sprawiają,
że ciała nie emitujące własnego światła, mają różne barwy. Ciało oświetlone światłem białym
jest barwy np. zielonej, jeżeli nie pochłania, a odbija zielone światło. Barwa ciała zależy też
od składu widmowego, czyli od przebiegu funkcji
M λ = f
promieniowania
T
(λ)
oświetlającego dane ciało. Ciało nazywamy szarym, jeżeli jego spektralny współczynnik
absorpcji praktycznie jest stały w dużym zakresie długości fal α λ = α = const . Ciało, które
T
T
by niezależnie od swojej temperatury i długości fali promieniowania całkowicie pochłaniało
padający na nie strumień energii promieniowania, nazywa się ciałem doskonale czarnym.
Zatem spektralny współczynnik absorpcji ciała doskonale czarnego, oznaczmy go symbolem
α , jest równy jedności niezależnie od długości fali i temperatury:
0 T
λ
α λ
(1.4)
T = 1
0
Ciało doskonale czarne jest ciałem wyidealizowanym. Ciała rzeczywiste zawsze odbijają s
absorpcji mniejszy od jedności. Do materiałów, których spektralny współczynnik absorpcji w
zakresie długości promieniowania widzialnego jest bardzo bliski jedności należą: sadza,
czerń platynowa, czarny aksamit. Najlepszym jednak przybliżeniem ciała doskonale czarnego
jest mały otwór w wnęce o powierzchni ścianek znacznie przekraczającej powierzchnię
otworu.
Jeżeli układ ciał odizolujemy termicznie, otaczając ciała doskonale odbijającą i nie
przepuszczalną dla promieni powłoką, wówczas w takim układzie po pewnym czasie dojdzie
do równowagi termicznej i wszystkie ciała osiągną jednakową i stałą temperaturę. Oznacza
to, że każde ciało układu w jednostce czasu emituje wtedy tyle samo energii co pochlania.
Zatem ciała, które dla określonych λ i T silnie absorbują promieniowanie (mają duże
wartości współczynnika α λ ) muszą je równocześnie intensywnie emitować, tzn.
T
charakteryzować się dużymi wartościami spektralnej emitancji M λ . Dobre absorbenty są
T
dobrymi emiterami. Opisaną powyżej sytuację możemy ująć w sposób bardziej formalny.
Rozważmy pewną liczbę ciał ( i = ,
1 2K n) znajdujących się w środku opisanej powyżej
powłoki, ze względu na równowagę termodynamiczną możemy napisać że energia
absorbowana i emitowana przez każde ciało w czasie ∆ t przez powierzchnię ∆ S dla fal od
i
λ do λ + dλ wynosi:
M
α
1λ ∆ S ∆ t
1
=
S
1λ ∆
∆ tI
1
M
S
α
2λ ∆ 2∆ t =
2λ ∆ S 2∆ tI (1.5)
M
M
α
λ∆ S ∆ t =
λ∆ S ∆ tI
n
n
n
n 1
gdzie I jest natężeniem promieniowania. Należy zauważyć, że ze względu na równowagę
termodynamiczną I jest izotropowe w każdym miejscu przestrzeni takie samo. Ciała
zanurzone są w kąpieli z promieniowania . Dzieląc lewe strony równań przez prawe i biorąc
pod uwagę stałość I otrzymujemy:
M
M
M
M
1λ Y
1λ T
nλ T
0λ T
=
= L =
=
α
α
α
(1.6)
1
1λ T
1λ T
nλ T
Wynik ten stanowi w praktyce treść prawa Kirchoffa. Prawo to głosi, ze dla dowolnego ciała
stosunek jego spektralnej emitancji do spektralnego współczynnika absorpcji jest jedna i tą
samą, uniwersalną funkcją długości fali i temperatury ciała:
M λ T = f (λ, T)
α
(1.7)
λ T
Oczywiście ostatnie równanie słuszne jest w szczególności dla ciała doskonale czarnego, dla
którego α λ
. Oznaczając przez M
spektralną emitancję ciała doskonale czarnego
T = 1
0
0λ T
możemy napisać:
M 0λ T = M
= f λ ,
0 T
( T )
α
λ
(1.8)
0 λ T
oraz
M
= α M
λ
(1.9)
T
λ T
0λ T
Uniwersalną funkcją f (λ, T ) jest więc funkcją rozkładu widmowego promieniowania ciała
doskonale czarnego M
. Na tym właśnie polega zasadnicze znaczenie modelu
0λ T
wyidealizowanego ciała czarnego, że funkcja rozkładu promieniowania tego modelu opisuje
właściwości ciał rzeczywistych. Z prawa Kirchoffa wyrażonego dwoma ostatnimi
związkami wynika, że jeżeli w danej temperaturze ciało nie pochłania promieniowania w
przedziale od λ do λ + dλ to nie może ono także promieniować w tym przedziale długości
fal (jeżeli αλ
, to M λ
). Z drugiej strony z tego, że spektralny współczynnik
T = 0
T = 0
absorpcji αλ jest bliski jedności nie wynika że duża jest spektralna emitancja ciała M
T
λ ,
T
gdyż w rozważanej temperaturze T ciało doskonale czarne może nie emitować fal w
rozważanym przedziale długości ( M
α
λ
). Ponieważ λ
więc zawsze M
< M tzn.
T < 1
T = 0
0
λ T
0λ T
ciało rzeczywiste słabiej promieniuje niż ciało doskonale czarne. Dla określonej temperatury
T = const wykresy funkcji rozkładu widmowego promieniowania ciał rzeczywistych w całym
zakresie długości fal leżą poniżej krzywej rozkładu widmowego ciała doskonale czarnego.
Korzystając z (1.9) można napisać, że:
∞
M
= ∫
(1.10)
T
αλ M
T
0λ T
λ
d
0
Promieniowanie ciała doskonale czarnego
Przed przystąpieniem do znalezienia rozkładu widmowego ciała doskonale czarnego
sformułujmy pewne postulaty. Rozpatrzmy doskonały absorber , ciało doskonale czarne, które
pochłania całość padającego promieniowania. Promieniowanie termiczne takiego ciała
będziemy nazywać promieniowaniem ciała doskonale czarnego. Mając taki doskonały
pochłaniacz promieniowania wprowadzimy jego model fizyczny. Modelem tym będzie duże
wydrążenie z małym otworem na zewnątrz, co powoduje że prawdopodobieństwo wydobycia
się na zewnątrz promienia, który wpadł do środka przez otwór, jest bardzo małe, o ile wnęka
jest dostatecznie duża. Otwór jest więc doskonałym absorberem, a ta część energii która
wycieka w przezeń z wewnętrznego pola promieniowania istniejącego we wnęce stanowi
promieniowanie ciała doskonale czarnego. Można podać następujące własności
promieniowania w jamie:
1. Równowagowy rozkład gęstości energii uλ tego pola zależy wyłącznie od
temperatury ścianek tzn. uλ ( T ) , które możemy uważać za doskonałe zwierciadła.
2. Promieniowanie jest izotropowe tzn. nie jest w żaden sposób ukierunkowane.
3. Promieniowanie jest równoważne emitowanemu przez ciało czarne.
4. Promieniowanie nie zależy od rodzaju materiału z którego są zbudowanie ściany
wydrążenia.
5. Promieniowanie nie zależy od kształtu wnęki.
Można wykazać, że jeżeli którekolwiek z powyższych stwierdzeń nie byłoby prawdziwe
to można by, dzięki odpowiedniemu rozmieszczeniu pochłaniaczy energii wewnątrz
wnęki, skonstruować maszynę cieplną, która pogwałciłaby II zasadę termodynamiki.
Biorąc pod uwagę punkt 1. możemy zapisać całkowitą gęstość energii, to jest energię
pochodzącą od wszystkich długości fal pola promieniowania wnęki na jednostkę objętości
jako :
∞
u = ∫ uλ λ
d (1.11)
0
Zakładamy, że pole promieniowania wnęki jest izotropowe (własność 2). W takim razie
ciśnienie wywierane na ściany wnęki (ciała doskonale czarnego) przez izotropowe
promieniowanie zależy od gęstości lokalnej gęstości pola jak:
1
p = u (1.12)
3
Przypuśćmy, że mamy wnękę o objętości V wypełnioną izotropowym promieniowaniem
o gęstości u . W tym przypadku I zasada termodynamiki dla takiego układu wygląda
następująco:
1
1
4
dQ = dU + pdV = d u
( V ) + udV = udV + Vdu + udV = Vdu + udV (1.13)
3
3
3
dzieląc dQ przez T absolutną temperaturę ścian wnęki otrzymujemy przyrost entropii
dQ
4
V u
∂
4 u
dS =
= Vdu + udV =
dT +
dV (1.14)
T
3
T T
∂
3 T
V
w ostatnim związku wzięliśmy pod uwagę postulat 1 mówiący o tym, że u jest tylko
funkcją temperatury. Wobec tego, że S( V , T ) jest funkcją stanu możemy napisać:
S
∂
S
∂
dS =
dT +
dV (1.15)
T
∂
V
∂
V
T
a poprzez to:
S
∂
V u
∂
S
∂
4 u
=
=
(1.16).
T
∂
T T
∂
V
∂
3 T
V
V
T
Korzystając z twierdzenia Schwartza
∂2 S
∂2 S
=
(1.17)
V
∂ T
∂
T
∂ V
∂
otrzymujemy:
1 u
∂
u
4
4 u
∂
= −
+
(1.18)
T T
∂
T
3 2
T
3 T
∂
V
V
wobec tego:
1 du
4 u
= −
(1.19)
2
3 T dT
3 T
rozwiązując to powyższe równanie różniczkowe otrzymujemy :
u( T )
4
= α T (1.20)
Jest to istotny rezultat mówiący, że całkowita gęstość energii promieniowania wnęki jest
proporcjonalna do 4-tej potęgi temperatury wyrażonej w kelwinach. Rezultat ten prowadzi
bezpośrednio do prawa Stefana-Boltzmanna, mówiącego że jednostka powierzchni ciała
doskonale czarnego wypromieniowuje całkowitą moc równą:
4
M
= T
σ (1.21)
0 T
Gdzie σ jest stał
−
ą Stefana-Boltzmanna
8
2
5.67 ×10 W / m . W ten sposób otrzymaliśmy
prawo opisujące moc wypromieniowaną przez element powierzchni ciała doskonale
czarnego używając praw termodynamiki.
Zadanie wyznaczenia postaci uλ ( T ) lub M
jednak pozostaje nam do rozwiązania.
0λ T