Gdańsk, 23.11.2010
LABORATORIUM METROLOGII
Ćwiczenie nr3:Pomiar częstotliwości i fazy
Sprawozdanie wykonała: AGNIESZKA KOSTRUBIEC
Kierunek:
IBM ; grupa 2
1.Obliczyć błąd systematyczny pomiaru korzystając z metody różniczki zupełnej, wiedząc ze błąd generatora podstawy czasu oscyloskopu wynosi 3%, i przyjmując błąd odczytu ekranu oscyloskopu 1mm.
Wykorzystując oscyloskop pomierzyłam wartości okresu XT oraz współczynnika podstawy czasu Dtx. Dane te wykorzystałam do policzenia częstotliwości sygnału fx według poniższego wzoru:
1
1
1
f =
=
=
= 2632 [ Hz]
x
X ⋅ D
7,6 ⋅ ,
0 00005
,
0 000038
T
TX
Błąd względny pomiaru :
∆ DXt ∆ X
1[ mm]
δ
fx =
+
T
⋅10 %
0
= 0
,
0 3 +
⋅10 %
0
= 0
,
0 3 + 0
,
0 1 ⋅10 %
0
= %
4
D
X
100 [ mm]
Xt
T
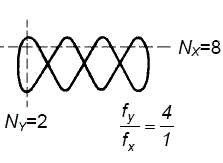
2. Załączyć rysunki figur Lissajous wykonane w p. 4.1.2. uzupełnione graficznym opisem sposobu wyznaczenia częstotliwości generatora HM 8032 (dla obu figur).
Na podstawie figur Lissajous możliwe jest obliczenie częstotliwości :
• metodą siecznych: - stosunek częstotliwości wyznacza się z ilorazu liczby przecięć prostej poziomej z figurą do liczby przecięć prostej pionowej z figurą.
Proste nie mogą przechodzić przez punkty węzłowe;
• metoda stycznych - stosunek częstotliwości oblicza się z ilorazu liczby punktów styczności z figurą, odpowiednio prostej poziomej i prostej pionowej przeprowadzonych stycznie do figury;
n
m
x
x
=
=
f
n
m
x
y
y
nx – liczba przecięć figury z prostą poziomą ny – z prostą pionową
mx – liczba punktów styczności z prostą poziomą my – z prostą pionową
Obliczenia:
figury pierwsza
figura druga
fy = 400Hz
fy = 400Hz
• - metoda siecznych: nx=4, ny=2;
• - metoda siecznych: nx=2,ny=4;
• - metoda stycznych: mx=2, my=1
• - metoda stycznych: nx=4,ny=2; f
f
y
n
m
2
=
y
n
m
1
x =
x =
= x = x =
f
n
m
1
f
n
m
2
x
y
y
x
y
y
f
f = 2 f = 200 Hz f
y
=
= 200 Hz
x
y
x
2
3. Uzupełnić tablice 2 i 3. Obliczyć maksymalne błędy systematyczne εϕ pomiarów kąta fazowego stosowanymi w ćwiczeniu metodami. Skorzystać z metody różniczki zupełnej. Błąd względny δϕ pomiaru przesunięcia fazowego wyznaczyć jako stosunek obliczonej wartości ε
ϕ
ϕ do teoretycznej wartości
.
teor
Sprawdzić, czy zmierzona wartość kąta przesunięcia fazowego mieści się w granicach wyznaczonego błędu względem obliczonej teoretycznej wartości ϕ
.
teor
R=993Ω
C=103nF
tg ϕ
(
) = ω RC
toer
ω = 2 fπ
rad
ω = 2π *1000 = 62831,8
s
)
toer
= 62831
, 8 * 993 * ,
0 000000103 = ,
0 6426
ϕ
teor = arctg ( , 0 6426) = 3 ,
2 7
Tablica 2:
X
t
o
7
,
0
0
0
ϕ =
360
=
3
60 = 33 6
,
X T
5
,
7
δϕ
X
∆
X
1
,
0
1
,
0
t
t
o
o
o
o
εϕ =
X
∆
=
+ ∆
360
=
+
3
60 = ( 0
,
0 13 + 0
,
0 017 3
) 60 = ,
5 29
T
X
δ
X
X 2
5
,
7
5 ,
6 25
T
T
T
,
5 290
δϕ =
100 % =16,2%
32 7
, o
3 ,
3 6 − 3 ,
2 7 < εϕ
0
9
,
0
< ,
5 29
Kąt mierzony mieści się w granicy błędu.
Tablica 3:
2 X
3
,
4
0
0
ϕ = ± arcsin
= arcsin
= arcsin( 5
,
0 37 )
5 = 32 5
, 1
2 X m
8
1
,
0
1
,
0 * 3
,
4
0
εϕ =
+
= ,
0 023 ≈ 3
,
1 2
,
6 75
53 9
, 7
3
,
1 2
δϕ =
∗100% = ,
4 03%
3 ,
2 7
32 5
, 1 − 32 7
,
= 1
,
0 9 < εϕ
W tym przypadku również kąt mierzony mieści się w granicy błędu.
4.Obliczyć wartość współczynnika wypełnienia w tablicy 4.
t
150 8
,
k
1
=
=
= 3
,
0 01 s
µ
obl
T
500
1
5.Obliczyć błąd dyskretyzacji w tablicy 5.
Skorzystałam ze wzoru :
1
δ
= 100 %
dyskr.
N
6.Porównać niestabilność obu generatorów.Policzyć niestabilność względną ε / f
f
dla generatorów ze wzoru:
ε
−
f
f
f
max
min
=
f
f nom
gdzie :
f
, f
odpowiednio maksymalna i minimalna wartość częstotliwości w serii max
min −
pomiarów,
f
- nominalna wartość częstotliwości generatora.
nom
Generator HM 8131-2 :
ε f 500 ,00103−500 ,00069
−7
=
= 8
,
6 ∗10
f
5000
Generator HM 8032 :
ε f 50008,93−5000
−4
=
= 7
,
1 ∗10
f
4999 9
,
Generator HM 8131-2 jest bardziej stabilny.