STANY NIEUSTALONE W OBWODACH RLC
Łoszajc Maciej – 62438
Wejman Małgorzata – 62501
1. CEL ĆWICZENIA:
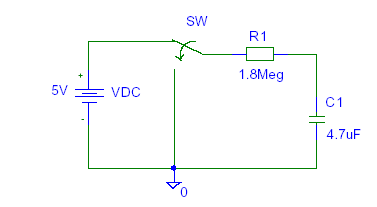
Analiza zachowania obwodu RLC w warunkach stanu nieustalonego. Badanie wpływu zmiany wartości rezystancji w obwodzie na czas trwania stanu nieustalonego.
Badany układ:
Dane:
R1 = 1,8 MΩ
C1 = 4,7 uF
U = 5 V
Stała czasowa obwodu:
1
τ =
= RC = 8
,
1 ×106 × 7
,
4 ×10−6 = ,
8 46 s
α
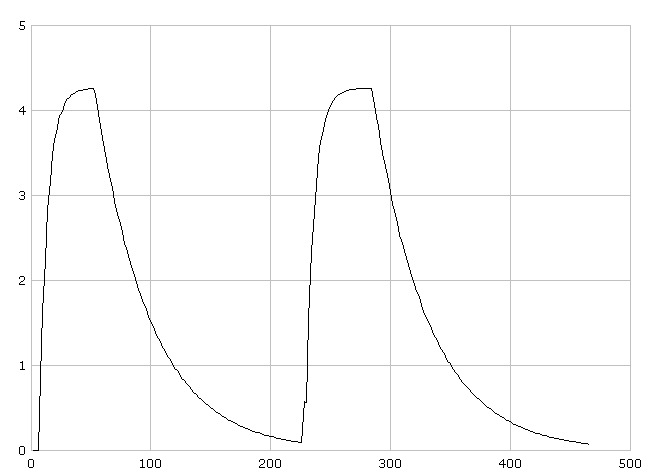
Pomiar spadku napięcia na pojemności (2 pełne cykle ładowania - rozładowania kondensatora): Obliczenia:
Obliczam wartość napięcia na kondensatorze metodą klasyczną. Zakładam, iŜ napięcie początkowe wynosi: U(0) = 5 V
Korzystając z prawa napięciowego Kirchoffa otrzymujemy:


Ri + u = 0
c
du
i
= C
c
dt
du
RC
c + u = 0
dt
c
du
u
0
c
c
+
=
dt
RC
RC
Aby obliczyć powyŜsze równanie układam równanie charakterystyczne dla powyŜszego równania róŜniczkowego: 1
s +
= 0
,
8 46
1
s = −
= − 1,
0 2
,
8 46
PoniewaŜ otrzymujemy pojedynczy pierwiastek równania charakterystycznego, otrzymujemy sygnał aperiodyczny:
− t
u t
( ) = Ae α
st
u t
( ) = Ae
−0 1
, 2 t
u t
( ) = Ae
Obliczam stałą całkowania korzystając z załoŜenia, iŜ napięcie początkowe u(0) = 5V, zatem A = 5. Otrzymuję ogólny wzór na napięcie postaci:
0
− 1
, 2 t
u( t) = e
5
2. STAN NIEUSTALONY W SZEREGOWYM UKŁADZIE RLC: Schemat badanego układu:
Dane:
R1 = 1 kΩ
L1 = 66 mH
C1 = 2,2 nF
Przebieg pomiarów:
Aby obliczyć przebieg napięcia na kondensatorze korzystam z prawa napięciowego Kirchoffa: u + u + u = e R
L
u
= Ri
R
u
= Li
L
du
i
= C
c
dt
du 2
du
L
c + RC
c + u = e dt 2
dt
du 2
R du
1
1
c
c
+
+
u =
e
dt 2
L dt
LC
LC
W celu obliczenia równania róŜniczkowego układam równanie charakterystyczne. Obliczenia przeprowadzam dla R = 1 kΩ
R
2
1
s +
s +
= 0
L
LC
2
s + 0
,
0 2 ×106 s + 8
,
6 8×109 = 0
0 4 ×109 − 27 5
, 2×109 = −27 ,
1 2 ×108
∆ =1 ,
6 46×104 j
− ,
0 02×106 ±1 ,
6 46×
4 j
s
α ω j
1/ 2 =
10
= − ±
2
α = −10000
ω = ,
8 23×104
u( t)
t
π
=
−10000
Ae
sinω t −
2
u(0) = 5 V
π
5 = A sin −
2
A = −5
t
π
u( t) = −
−
5 10000
e
sinω t −
2
Obliczam wzór na przebieg napięcia u(t) dla rezystancji równej 100 Ω: R
2
1
s +
s +
= 0
L
LC
2
s + 5
,
1 1×103 s + 8
,
6 8 ×109 = 0
∆ = ,
2 28 ×106 − 27520 ×106 = −2751 , 7 72 ×106
∆ =165 8
, 8 ×103 j
− 5
,
1 1×103 ± 165 8
, 8 ×
3 j
s
α ω j
1 / 2 =
10
= − ±
2
α = −755
ω = 82940
u( t)
t
π
=
−755
Ae
sinω t −
2
u(0) = 5 V
π
5 = A sin −
2
A = −5
t
π
u( t) = −
−
5 755
e
sinω t −
2
Obliczam wzór na przebieg napięcia u(t) dla rezystancji równej 10 kΩ: R
2
1
s +
s +
= 0
L
LC
2
s + 1
,
0 5×106 s + 8
,
6 8×109 = 0
, ×109 − 27 5
, 2 ×109 = −5 ,
0 2 ×108
∆ = 5 ,
0 2 ×104 j
− 1
,
0 5×106 ± 5 ,
0 2 ×
4 j
s
α ω j
1/ 2 =
10
= − ±
2
α = −75000
ω = 251000
u( t )
t
π
=
−75000
Ae
sinω t −
2
u(0) = 5 V
π
5 = A sin −
2
A = −5
π
u( t) = −
−
5 75000
e
sinω t −
2
Obliczam wzór na przebieg napięcia u(t) dla rezystancji równej 100 kΩ: R
2
1
s +
s +
= 0
L
LC
2
s + 5
,
1 ×106 s + 8
,
6 8×109 = 0
9
9
8
∆ = 2250×10 − 27 5
, 2 ×10 = 22224 8
, ×10
4
∆ = 149 0
, 8 ×10
s = 4
− 600
1
s = −1495400
2
u( t)
−4600 t
1
− 495400 t
= A e
+ A e
1
2
u'( t)
−4600 t
1
− 495400 t
= −4600 A e
−1495400 A e
1
2
u(0) = V
5
5
= A + A
1
2
0
= −4600 A −1495400 A 1
2
A = − 0
,
0 1
1
A = 0
,
5 1
2
A = −5
u( t)
−4600 t
1
− 495400 t
= − 0
,
0
e
1
+ 0
,
5
e
1
Obliczam wzór na przebieg napięcia u(t) dla rezystancji równej 1 MΩ: 2
R
1
s +
s +
= 0
L
LC
s 2 + 15 1
, 5 ×106 s + 8
,
6 8 ×109 = 0
∆ = 229 5
, ×1012 − 27 5
, 2 ×109 = ,
2 295 ×1014
∆ = 5
,
1 15 ×107
s = 0
1
s = 1
− 51
, 5 ×106
2
6
u( t) = A + A e 15 1,5 1
× 0 t
1
2
6
u'( t) = 15 1
, 5 ×106 A e 15 1,5 1
× 0 t
2
u(0) = V
5
5
= A + A
1
2
0
= 15 1
, 5 ×106 A 2
A = 5
1
A = 0
2
u( t) = V
5
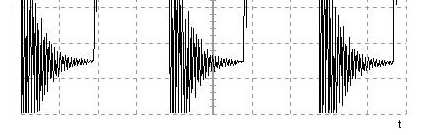
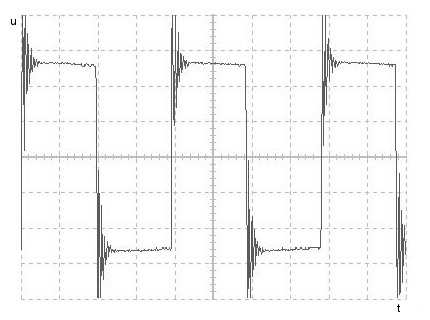
3. WYKRESY DLA POSZCZEGÓLNYCH OBLICZEŃ: Wykres u(t) dla rezystancji równej 0,1 kΩ
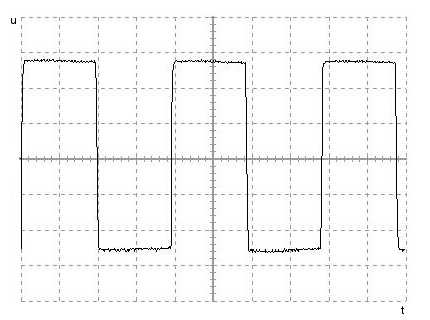
Wykres u(t) dla rezystancji równej 1 kΩ
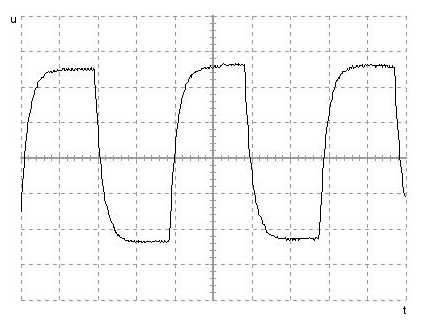
Wykres u(t) dla rezystancji równej 10 kΩ
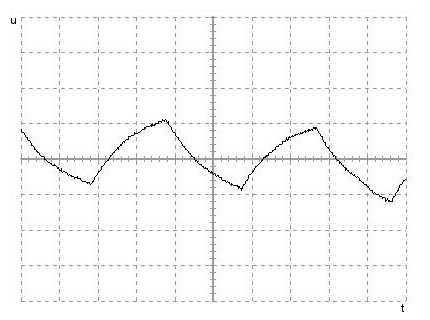
Wykres u(t) dla rezystancji równej 100 kΩ
Wykres u(t) dla rezystancji równej 1 MΩ
4. WNIOSKI:
Jak moŜemy łatwo zauwaŜyć wyniki przeprowadzonych obliczeń teoretycznych są zbliŜone do przebiegu napięcia przedstawionego na wykresie, a pochodzącego z wykonanych pomiarów.
Opór w układzie pełni funkcję tłumiącą i jednocześnie zwalniającą proces ładowania i rozładowywania kondensatora.
Im większy opór w układzie tym proces ładowania kondensatora przebiega wolniej.
Stała czasowa układu jest wprost proporcjonalna do oporu układu i pojemności kondensatora, wyraŜa się wzorem: τ = RC
Przebieg napięcia dla poszczególnych (dobranych zgodnie z treścią zadania) oporów przedstawione na powyŜszych wykresach zgadzają się z przeprowadzonymi pomiarami stanu nieustalonego (tuŜ po przełączeniu napięcia).
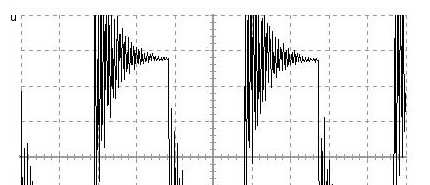
Dla oporów (100Ω; 1kΩ; 10kΩ) w wyniku obliczeń otrzymujemy liczby zespolone, które świadczą o występowaniu w układzie sygnału okresowego/periodycznego tłumionego, co doskonale widać na trzech pierwszych wykresach.
Dla oporów (100kΩ; 1 MΩ) otrzymujemy wyniki rzeczywiste co świadczy o obecności w układzie sygnału aperiodycznego.