


Blok 8: Ruch harmoniczny.
Wahadło matematyczne
ZESTAW ZADAŃ NA ZAJĘCIA
Uwaga: w poniŜszych zadaniach przyjmij, Ŝe wartość przyspieszenia ziemskiego jest równa
2
| g |= 10 m / s .
RUCH HARMONICZNY
1. W ruchu harmonicznym klocka o masie m = 1
,
0 kg zaczepionego na spręŜynie i
poruszającego się po poziomym stole bez tarcia, zaleŜność połoŜenia klocka od czasu wyraŜa si
π
ę wzorem: x(t) = 1
,
0 5 sin(4π ⋅ t + ) , gdzie stałe podane są w podstawowych jednostkach
2
SI, a x = 0 jest połoŜeniem równowagi. Oblicz: amplitudę, fazę początkową, okres, częstość drgań, maksymalne przyspieszenie, maksymalną prędkość, całkowitą energię mechaniczną układu. Oblicz, w jakiej odległości od połoŜenia równowagi znajdował się klocek w chwili t = 0 .
2. W ruchu harmonicznym zaleŜność połoŜenia ciała o masie m = ,
0 05 kg od czasu wyraŜa się
wzorem: x(t) = ,
0 02 sin 1
( 2π ⋅ t + )
π , gdzie stałe podane są w podstawowych jednostkach SI, a
x = 0 jest połoŜeniem równowagi. W chwili t = T / 4 , gdzie T jest okresem drgań ciała, oblicz: fazę ruchu, wartość prędkości chwilowej, wartość przyspieszenia chwilowego, wartość siły spręŜystości, energię kinetyczną i energię potencjalną spręŜystości.
3. W ruchu harmonicznym zaleŜność połoŜenia ciała od czasu wyraŜa się wzorem:
x(t) = 1
,
0 sin(7π ⋅ t) , gdzie stałe podane są w podstawowych jednostkach SI, a x = 0 jest połoŜeniem równowagi. W chwili, gdy wychylenie ciała z połoŜenia równowagi jest równe połowie amplitudy i zgodne ze zwrotem wybranej osi OX, oblicz:
• ile razy energia kinetyczna jest większa od energii potencjalnej
spręŜystości
• stosunek wartości prędkości chwilowej ciała do wartości prędkości
maksymalnej
• stosunek wartości przyspieszenia chwilowego ciała do wartości
przyspieszenia maksymalnego
4. ZaleŜność energii całkowitej oscylatora harmonicznego od amplitudy drgań przedstawiono na wykresie:
5. Aby rozciągnąć pojedynczą spręŜynę o ∆x naleŜało zadziałać siłą o wartości F. SpręŜynę rozcięto na dwie połowy. Siłą o jakiej wartości naleŜy zadziałać, aby rozciągnąć jedną z połówek o ∆x ?
Projekt jest współfinansowany z Europejskiego Funduszu Społecznego
w ramach programu operacyjnego KAPITAŁ LUDZKI
1
BLOK 8


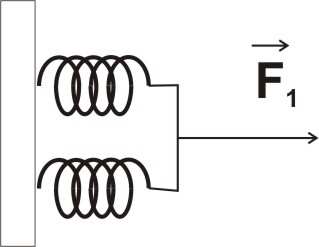
6. Aby rozciągnąć spręŜynę o 2 cm naleŜało zadziałać siłą o wartości 1 N. Jaką siłą naleŜy zadziałać, aby rozciągnąć spręŜynę o kolejne 2 cm?
7. Pojedynczą spręŜynę rozciągamy w taki sposób, aby siła powodująca
odkształcenie zawsze równowaŜyła aktualną siłę spręŜystości. Przy
wydłuŜeniu pojedynczej spręŜyny o x1 siła spręŜystości ma wartość 1
F .
Oblicz rozciągnięcie kaŜdej ze spręŜyn w przypadku pokazanym na
rysunku, gdy dwie takie spręŜyny połączymy i zadziałamy na nie siłą o
wartości 1
F .
8. Praca wykonana przy rozciąganiu układu spręŜyn z poprzedniego zadania jest: A) cztery razy mniejsza niŜ w przypadku rozciągania jednej spręŜyny siłą o wartości 1
F
B) dwa razy mniejsza niŜ w przypadku rozciągania jednej spręŜyny siłą o wartości 1
F
C) taka sama jak w przypadku rozciągania jednej spręŜyny siłą o wartości 1
F
D) dwa razy większa niŜ w przypadku rozciągania jednej spręŜyny siłą o wartości 1
F
E) cztery razy większa niŜ w przypadku rozciągania jednej spręŜyny siłą o wartości 1
F
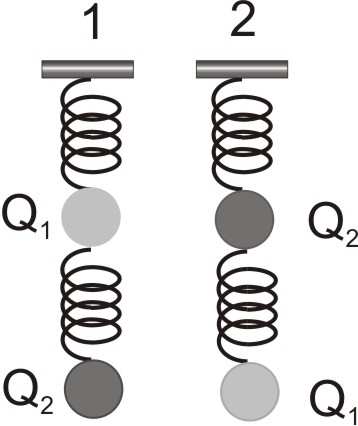
9. Dwie identyczne spręŜyny oraz dwie kule o cięŜarach Q1 i Q2
( Q >
2
Q1) zawieszono kolejno tak, jak na rysunkach. WydłuŜenia
x1 i x 2 górnej spręŜyny oraz y1 i y2 - dolnej w obu przypadkach
spełniają zaleŜność:
A) x =
1
x 2 i y =
1
y 2
B) x =
1
x 2 i y >
1
y 2
C) x <
1
x 2 i y >
1
y 2
D) x <
1
x 2 i y =
1
y 2
WAHADŁO MATEMATYCZNE
10. Kuleczka na nici stanowi wahadło matematyczne. Jeśli masę kuleczki zwiększymy czterokrotnie a długość nici zmniejszymy dwukrotnie, to ile razy zmieni się okres drgań wahadła?
11. Wahadło matematyczne o okresie zawieszono w windzie i wyznaczono okres jego drgań własnych: T = 5 s , gdy winda spoczywa. Oblicz okres drgań wahadła, jeŜeli winda:
• porusza się w górę z przyspieszeniem
m
a = 3
2
s
• porusza się w górę z opóźnieniem
m
a = 3
2
s
12. Wahadło matematyczne o okresie T = 5 s zawieszono w autobusie. Oblicz okres drgań wahadła, jeŜeli autobus:
• rusza z przystanku z przyspieszeniem
m
a = 2
2
s
• hamuje z opóźnieniem
m
a = 2
2
s
Projekt jest współfinansowany z Europejskiego Funduszu Społecznego
w ramach programu operacyjnego KAPITAŁ LUDZKI
2
BLOK 8


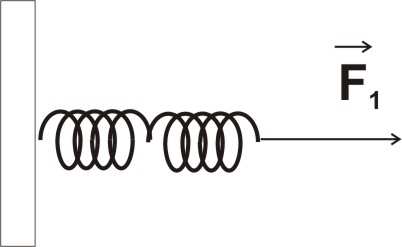

ZESTAW ZADAŃ DO SAMODZIELNEGO ROZWIĄZANIA
1. Pojedynczą spręŜynę rozciągamy w taki sposób, aby siła
powodująca odkształcenie zawsze równowaŜyła aktualną siłę
spręŜystości. Przy wydłuŜeniu pojedynczej spręŜyny o x1 siła
spręŜystości ma wartość 1
F . Oblicz rozciągnięcie kaŜdej ze
spręŜyn w przypadku pokazanym na rysunku, gdy dwie takie
spręŜyny połączymy i zadziałamy na nie siłą o wartości 1
F .
2. ZaleŜność okresu drgań wahadła matematycznego od jego długości poprawnie przedstawiono na wykresie:
3. Na dwóch spręŜynach o współczynnikach spręŜystości k1 i k 2 i jednakowych długościach początkowych, zaczepionych u sufitu zawieszono cięŜarki o jednakowych masach. JeŜeli wydłuŜenie spręŜyny (2) jest dwa razy większe od wydłuŜenia spręŜyny (1), to:
A) k = ⋅
1
2 k 2
B) k = ⋅
1
4 k 2
C) k =
1
k 2
D) 2 ⋅ k =
1
k 2
4. Ciało wykonuje drgania harmoniczne. W połoŜeniu równowagi:
A) szybkość ciała osiąga wartość maksymalną, a przyspieszenie jest równe zeru
B) przyspieszenie ciała osiąga wartość maksymalną, a szybkość jest równa zeru
C) szybkość i przyspieszenie przyjmują wartości maksymalne
D) szybkość i przyspieszenie przyjmują wartości minimalne
5. Na spręŜynie o małej masie zwieszono ciało o masie 1 kg. Oblicz okres drgań tego odwaŜnika, jeŜeli pod wpływem siły 1 N spręŜyna wydłuŜa się o 0,5 cm.
6. W tym samym czasie jedno z dwóch wahadeł matematycznych wykonało 12 pełnych wychyleń, zaś drugie z nich – 18 pełnych wychyleń. RóŜnica długości wahadeł wynosi 10 cm.
Oblicz długości wahadeł.
7. Oblicz energię potencjalną ciała o masie m = 1
,
0 kg wykonującego drgania harmoniczne o
amplitudzie A = 30 mm z częstotliwością f = 20 Hz po czasie t
1
= T od wychylenia z
4
połoŜenia równowagi.
Projekt jest współfinansowany z Europejskiego Funduszu Społecznego
w ramach programu operacyjnego KAPITAŁ LUDZKI
3
BLOK 8


