Informatyka
Grupa 11
Laboratorium Technik Cyfrowych
nr 3
Funkcja logiczna może być w ogólnym przypadku przedstawiona za pomocą wielu
różnych mniej lub bardziej skomplikowanych funkcji logicznych. Zagadnienie
minimalizacji polega na wyznaczeniu dla danej funkcji tej formuły, która jest
najprostsza. Zagadnienie to formułuje się też inaczej – dla danej funkcji logicznej
należy wyznaczyć możliwą najprostszą funkcję równoważną.
Minimalizacja funkcji logicznej wiąże się z porównaniem stopnia skomplikowania
funkcji.
Metody minimalizacji funkcji logicznych można podzielić na dwie grupy. Do pierwszej
grupy należą metody przekształceń algebraicznych. Metody te nie są zbyt przydatne w
praktyce. Do drugiej grupy należą metody algorytmiczne.
Podstawową rzeczą jest stworzenie tabeli prawdy, z której korzystamy niezależnie od
wybranego przez nas sposobu.
Układy cyfrowe to rodzaj układów elektronicznych, w których sygnały napięciowe
przyjmują tylko określoną liczbę poziomów, którym przypisywane są wartości
liczbowe. Najczęściej (choć nie zawsze) liczba poziomów napięć jest równa dwa, a
poziomom przypisywane są cyfry 0 i 1, wówczas układy cyfrowe realizują operacje
zgodnie z algebrą Boole’a i z tego powodu nazywane są też układami logicznymi.
Obecnie układy cyfrowe budowane są w oparciu o bramki logiczne realizujące
elementarne operacje znane z algebry Boola: iloczyn logiczny (AND, NAND), sumę
logiczną (OR, NOR), negację NOT, różnicę symetryczną (XOR) itp. Ze względu na
stopień skomplikowania współczesnych układów wykonuje się je w postaci układów
scalonych.
Bramka logiczna 9 element konstrukcyjny maszyn i mechanizmów (dziś zazwyczaj:
układ scalony, choć podobne funkcje można zrealizować również za pomocą innych
rozwiązań technicznych, np. hydrauliki czy pneumatyki), realizujący fizycznie pewną
prostą funkcję logiczną, której argumenty (zmienne logiczne) oraz sama funkcja mogą
przybierać jedną z dwóch wartości, np. 0 lub 1 (zob. algebra Boole’a).
Podstawowymi elementami logicznymi, stosowanymi powszechnie w budowie układów
logicznych, są elementy realizujące funkcje logiczne: sumy (alternatywy), iloczynu
(koniunkcji) i negacji. Są to odpowiednio bramki OR, AND i NOT. Za pomocą dwóch
takich bramek (np. OR i NOT lub AND i NOT) można zbudować układ, realizujący
dowolną funkcję logiczną.
Bramki NAND (negacja koniunkcji), oraz NOR (negacja sumy logicznej) nazywa się
funkcjonalnie pełnymi ponieważ przy ich użyciu (tzn. samych NAND lub samych NOR)
można zbudować układ realizujący dowolną funkcję logiczną.
Dowolną bramkę logiczną można też skonstruować za pomocą pary bramek, np. za
pomocą OR i NOT lub AND i NOT. Układy takie nazywamy układami zupełnymi.
Bramkę logiczną XOR często wykorzystujemy w układach arytmetyki takich jak
sumatory czy subtraktory.
1

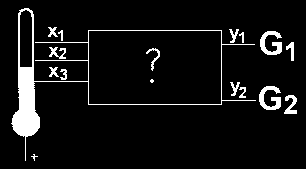
1. Zagadnienie
Zadaniem w tym ćwiczeniu jest sporządzenie układu logicznego obsługującego
poniższy schemat:
Założenia:
9 X1, X2, X3 oznaczają czujniki, które informują układ czy dana temperatura została
osiągnięta
9 G1, G2 to są grzałki, które uruchamiają się jeśli zostanie osiągnięta odpowiednia dla
nich temperatura,
9 przyjąłem, że czujnik X1 (dla pozostałych tak samo) emituje „1” jeśli temperatura
osiągnie lub będzie większa od T1,
9 grzałki uruchamiają się gdy otrzymają sygnał „1”, a wyłączają przy sygnale „0”,
9 moc grzewcza G1 jest większa od G2.
2. Analiza schematu
W przypadku zadań 3 i 4 mamy zbudować układ logiczny na podstawie tabeli prawdy.
W zadaniu 4 należy zminimalizować układ kombinacyjny wg. tabeli Karnaugha. W
zadaniu 6 musimy zbudować układ logiczny odporny na awarie. Przyjąć założenie, że
może być uszkodzony jeden czujnik i pokazywać wtedy trwale stan „0” albo „1”.Należy
przeanalizować ponownie tabelę prawdy i w niejasnych sytuacjach wpisać wartość „0”
lub „1”. Awarię jednego z czujników rozpoznamy wtedy, gdy czujnik wyższej
temperatury pokazuje, że temperatura została osiągnięta, a czujnik niższej pokazuje,
że ta nie została osiągnięta. Nie jesteśmy jednak w stanie rozpoznać czy czujnik X3
uległ awarii i zwraca stale wartość „0”. Przyjmuje, że maksymalnie jeden czujnik może
ulec awarii a także że w przypadku niejednoznacznym ważniejsze jest by nie
przekroczyć mocy grzewczej układu.
X1 X2 X3 G1 G2
0 0 0 1 1
0 0 1 1 0
0 1 1 0 1
1 1 1 0 0
2
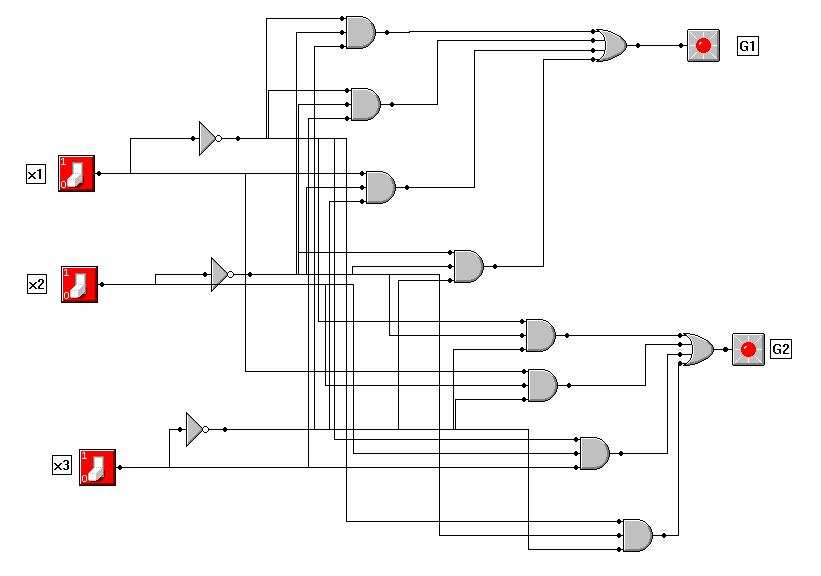
Zbudować wariant nieoptymalny (wg tabeli prawdy).
Wariant nieoptymalny wg tabeli prawdy:
G1 = (~X1 AND ~X2 AND ~X3) OR (~X1 AND ~X2 AND ~X3) OR (X1 AND ~X2 AND ~X3)
OR (~X1 AND ~X2 AND ~X3)
G2 = (~X1 AND ~X2 AND ~X3) OR (X1 AND X2 AND ~X3) OR (~X1 AND X2 AND X3)
OR (~X1 AND ~ X2 AND ~X3)
Tabela prawdy dla G1:
X1 X2 X3 ~X1 ~X2 ~X3 ~X1 * ~X2 * ~X3 ~X1 * ~X2 * ~X3 X1 * ~X2 * ~X3 CAŁOŚĆ
0 0 0
1
1
1
1
0
0
1
0 0 1
1
1
0
0
1
0
1
0 1 1
1
0
0
0
0
0
0
1 1 1
0
0
0
0
0
0
0
Tabela prawdy dla G2:
X1 X2 X3 ~X1 ~X2 ~X3 ~X1 * ~X2 * ~X3 X1 * X2 * ~X3 ~X1 * X2 * X3 CAŁOŚĆ
0 0 0
1
1
1
1
0
0
1
0 0 1
1
1
0
0
0
0
0
0 1 1
1
0
0
0
0
1
1
1 1 1
0
0
0
0
0
0
0
3
3. Zbudować wariant minimalny najprostszy układ kombinacyjny (wg tabeli
Karnaugha).
Metoda tabeli Karnaugha – grzałka G1.
X
1 \ X2 X3
00 01 11 10
0
1
1
0
x
1
x
x
0
x
Grupuję jedynkami. Nie zmienia się X2, jego wartość to „0”. Otrzymujemy następujący
wynik po zastosowaniu metody tabeli Karnahugha.
G1 = ~X2
Metoda tabeli Karnaugha – grzałka G2.
X
1 \ X2 X3
00 01 11 10
0
1
0
1
x
1
x
x
0
x
Grupuję jedynkami. Otrzymuję dwie grupy. W pierwszej grupie (czerwonej) nie
zmienia się X1, jego wartość to „0” oraz X2, jego wartość to „1”. W drugiej grupie
(niebieskiej) nie zmienia się X3, jego wartość to „0”. Otrzymujemy następujący wynik
po zastosowaniu metody tabeli Karnahugha.
G2 = (~X1 AND X2) OR ~X3
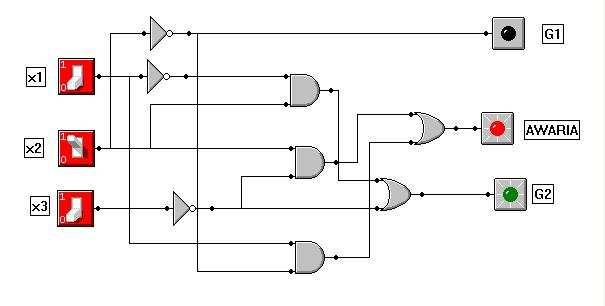
Uwzględniając zminimalizowane funkcje dla grzałek otrzymuję następujący schemat
logiczny:
4
Tabela prawdy dla zminializowanej funkcji grzałki G2.
X1 X2 X3 ~X1 ~X3 ~ X1 AND X2 (~X1 AND X2) OR ~ X3
0 0 0
1
1
0
1
0 0 1
1
0
0
0
0 1 1
1
0
1
1
1 1 1
0
0
0
0
6. Zbudować układ uwzględniający możliwość awarii czujników.
Zbudujemy teraz układ odporny na awarię termometru. Awaria występuje wtedy kiedy
czujnik wyższej temperatury odnotowuje, że temperatura została osiągnięta a czujnik
niższej temperatury nie odnotowuje. Możliwe kombinacje trzech czujników.
X1 X2 X3 WYNIK
0 0 0 DZIAŁA
0 0 1 DZIAŁA
0 1 0 AWARIA
0 1 1 DZIAŁA
1 0 0 AWARIA
1 0 1 AWARIA
1 1 0 AWARIA
1 1 1 DZIAŁA
Minimalizacja układu metodą tabeli Karnaugha.
X1 \ X2 X3 00 01 11 10
0
0
0
0
1
1
1
1
0
1
Otrzymujemy dwie grupy. W pierwszej grupie (czerwonej) nie zmienia się X2, ma
wartość „1” oraz X3 i ma wartość „0”. W drugiej grupie (niebieskiej) nie zmienia się X1,
ma wartość „1” oraz X2 i ma wartość „0”.
Wynik po minimalizacji: (X2 AND ~X3) OR (X1 AND ~X2)
5
Tabela prawdy dla układu czułego na awarię:
X1 X2 X3 ~X2 ~X3 X2 AND ~X3 X1 AND ~X2 (X2 AND ~X3) OR (X1 AND ~X2)
0 0 0
1
1
0
0
0
0 0 1
1
0
0
0
0
0 1 0
0
1
1
0
1 AWARIA
0 1 1
0
0
0
0
0
1 0 0
1
1
0
1
1 AWARIA
1 0 1
1
0
0
1
1 AWARIA
1 1 0
0
1
1
0
1 AWARIA
1 1 1
0
0
0
0
0
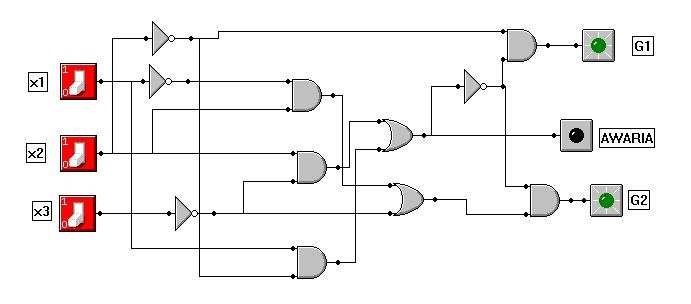
Jest jednak pewna wada powyższego układu jeśli zepsuje się czujnik X3 to grzejnik G2
będzie cały czas grzał. Aby zapobiec takiej sytuacji zmodyfikowałem schemat w taki
sposób, że połączyłem wyjście alarmowe z czujnikami i w momencie zaistnienia awarii
automatycznie wyłączane są oba czujniki.
6
Wnioski:
Przy użyciu bramek logicznych udało nam się zbudować układ kontroli grzejników ze
względu na daną temperaturę. Bezpośrednio z tabeli prawdy uzyskaliśmy
skomplikowany schemat. Po minimalizacji funkcji logicznych metodą tabeli Karnaugha
udało nam się znacznie mniejszych ilość użytych bramek logicznych.
Udało mi się również stworzyć układ odporny na awarię. Niestety nie jestem w stanie
zbudować schematu odpornego na awarię czujnika X3, ponieważ nie da się stworzyć
takiej kontroli na wejściu.
7