Poz.3.4.1. Zestawienie obciążeń obliczeniowych
Obciążenia stałe:
ciężar własny warstw:
4,20 · 5,70 · 7,95 = 190,3 kN
c. wł. żebra: (0,3 – 0,1) · 0,45 · 5,70 · 25,0 · 1,1 · 4 = 56,4 kN
c. wł. podciągu: (1,0 – 0,1) · 0,45 · 7,95 · 25,0 · 1,1 = 88,5 kN
c. wł. słupa:
0,45 · 0,45 · 5,3 · 25 · 1,1 = 29,5 kN
__________________
razem: 364,7
kN
Obciążenia zmienne:
grunt:
19,86 · 5,70 · 7.95 = 922,2 kN
śnieg:
0,98 · 5,70 · 7,95 = 44,4 kN
Obciążenie całkowite:
N = 364,7 + 922,2 + 44,4 = 1331,3 kN
Sd
Obciążenie długotrwałe:
N
= 364,7 + 922,2 = 1286,9 kN
Sd,lt
Moment zginający: M = 0,0 kNm Sd
mimośród statyczny e = 0
e
Poz.3.4.2. Wymiarowanie
Minimalne pole przekroju zbrojenia podłużnego: N
A
= max {0,15 · Sd ; 0,003 · } =
s,min
Ac
f yd
1331,3
= max {0,15 ·
= 5,7 ; 0,003 · 0,452 = 6,07} = 6,07 cm2
3
350 ⋅10
Dla słupa przyjęto otulinę 30 mm oraz zbrojenie symetryczne prętami φ25 oraz strzemionami pojedynczymi φ6.
przyjęto wstępnie zbrojenie 4φ25 (w narożach) A =
= 2 · 4,91 = 9,82 cm2 >
= 6,07 cm2
s1
As2
As,min
l = 5,30 m;
col
l = 0,7 ·
= 0,7 · 5,30 = 3,71 m
o
lcol
42
mimośród niezamierzony
l
530
h
45
e = max { col =
= 0,88 cm;
=
= 1,5 cm; 1,0 cm } = 1,5 cm
a
600
600
30 30
e = + = 1,5 + 0,0 = 1,5 cm o
ea
es
l
3,71
o =
= 8,2 > 7 – należy uwzględnić wpływ smukłości i obciążeń h
0,45
długotrwałych
umowna siła krytyczna
⎡
⎛
⎞
⎤
9 ⎢ E ⋅ I ⎜ 0,11
⎟
⎥
cm
c
N
=
⋅ ⎢
⎜
+ 0,1⎟ + E ⋅ I ⎥
crit
2
l
2
s
s
⋅ k
e
o
⎢
⎜ 0,1
o
lt
+
⎟
⎥
⎣
⎝
h
⎠
⎦
E = 32 GPa ; = 200 GPa
cm
Es
Końcowy współczynnik pełzania betonu φ(∞, t ), odczytano z tablicy o
A.1 normy, dla B37, wieku betonu w chwili obciążenia 90 dni, przy wilgotności względnej 80 % i dla miarodajnego wymiaru przekroju 2
2 ⋅ A
2 ⋅ 0,45
c
h =
=
= 0,225 m
o
u
4 ⋅ 0,45
wynosi: φ(∞, t ) = 1,35
o
N
1286,9
k = 1 + 0,5 ·
Sd , lt · φ(∞, ) = 1 + 0,5 ·
· 1,35 = 1,65
lt
to
N
1331,3
Sd
3
b ⋅ h
4
0,45
I =
=
= 3,42 · 10–3 m4
c
12
12
I = 2 ·
· (
s
As1
h/2 – a)2 =
= 2 · 9,82 · 10−4 · (0,45/2 – 0,03 – 0,025/2)2 = 6,541 · 10−5 m4
do wzoru na siłę krytyczną należy podstawić: e
l
o ≥ max {0,05; 0,5 – 0,01 · o − 0,01 · f }
cd
h
h
43
1,5
o =
= 0,033 m
h
45
max {0,05; 0,5 – 0,01 · lo − 0,01 · f } =
cd
h
= {0,05 ; 0,5 – 0,01 · 8,2 − 0,01 · 20 = 0,218} = 0,218 m przyjęto eo = 0,218 m
h
⎡
⎛
⎞
⎤
9 ⎢ E ⋅ I ⎜ 0,11
⎟
⎥
cm
c
N
=
⋅ ⎢
⎜
+ 0,1⎟ + E ⋅ I ⎥ =
crit
2
l
2
s
s
⋅ k
e
o
⎢
⎜ 0,1
o
lt
+
⎟
⎥
⎣
⎝
h
⎠
⎦
9
⎡32⋅3,42 ⎛
0,11
⎞
⎤
=
-2
⋅
+ 0,1 + 200 ⋅ 6,541⋅10 =
2
3,71 ⎢⎣ 2 1,65 ⎜⎝ 0,1 0,218
⎟
⎥
⋅
+
⎠
⎦
= 18,22 MN
zwiększony mimośród uwzględniający wpływ smukłości
1
1
η =
=
= 1,08
N
1,3313
1
Sd
−
1−
N
18,22
crit
e = η · = 1,08 · 0,015 = 0,016 m tot
eo
nośność słupa
e =
= 0,45/2 – 0,03 – 0,025/2 − 0,016 = 0,166 m s2
h/2 – a − etot
e =
= 0,45/2 – 0,03 – 0,025/2 + 0,016 = 0,198 m s1
h/2 – a + etot
2 ⋅(1−ξ
⋅ − ξ
eff )
2 (1 eff )
κ =
−1 =
−1 = 3,25 − 4,25 · ξ
s
1− ξ
1− 0,53
eff
eff ,lim
równanie równowagi momentów względem miejsca przyłożenia siły
⎛
+
2
e
a ⎞
s 2
α ⋅ f ⋅ b ⋅ d ⋅ξ ⋅ 0,5⋅ξ −
− f ⋅ A ⋅ e − κ ⋅ f ⋅ A ⋅ e = 0
cc
cd
eff
⎜
eff
⎟
yd
1
s
s 2
s
yd
1
s
1
s
⎝
d
⎠
podstawiając dane:
44
−
3
2
0,166 0,042 ⎞
0,85⋅ 20 ⋅10 ⋅ 0,45 ⋅ 0,407 ⋅ξ ⋅ 0,5⋅ξ −
−
eff
⎜
eff
0,407
⎟
⎝
⎠
3
−4
350
−
⋅10 ⋅9,82 ⋅10 ⋅0,166 −
−(3,25 − 4,25⋅ξ
−
⋅
⋅
⋅
⋅
⋅
=
eff )
3
4
350 10 9,82 10
0,198 0
co po przekształceniach daje:
ξ 2 − 0,1529 · ξ − 0,4391 = 0
eff
eff
otrzymano:
ξ = 0,7435 > ξ
= 0,53 – przypadek małego mimośrodu eff
eff,lim
(zbrojenia A i
są ściskane)
s1
As2
ponieważ ξ < 1 i ξ > ξ
eff
eff
eff,lim
κ = 3,25 − 4,25 · ξ = 3,25 − 4,25 · 0,743 = 0,092
s
eff
Z równania sumy sił wyznaczono N
Rd
N = α · ·
+ ·
− κ · ·
=
Rd
cc
fcd b · d · ξ eff fyd As2
s
fyd As1
= 0,85 · 20 · 0,45 · 0,407 · 0,743 + 350 · 9,82 · 10−4 −
− 0,092 · 350 · 9,82 · 10−4 = 2625,4 kN
N = 2625,4 kN >
= 1331,3 kN – warunek spełniony
Rd
N
Sd
podstawowy rozstaw strzemion:
15φ = 15 · 25 = 375 mm – przyjęto 350 mm zagęszczony rozstaw strzemion (w miejscach połączenia prętów podłużnych): 175 mm
Poz.3.5. Stopa fundamentowa
Założono ostrosłupowy kształt stopy fundamentowej.
Wysokość stopy powinna być większa niż długość zakotwienia prętów podłużnych słupa tj.:
l ≈ 30 · φ = 30 · 25 = 750 mm b
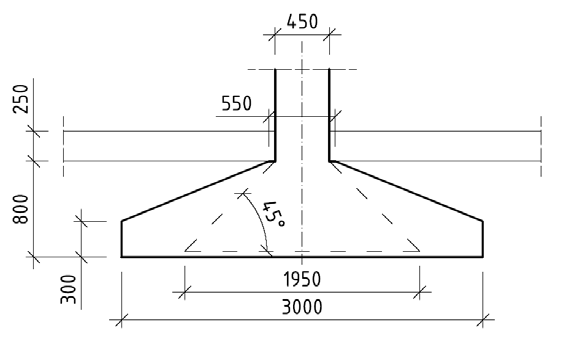
Przyjęto wymiary stopy (rys. __.8.): wysokość stopy: h = 0,80 m
podstawa stopy: B x L = 3,0 x 3,0 m grubość skrajna stopy: w = 0,30 m szerokość odsadzek: a = 0,55 m.
1
45
Rys. __.8. Wymiary stopy fundamentowej W niniejszym przykładzie pominięto obliczenia oporu granicznego podłoża. Uwagę skupiono na zaprojektowaniu stopy jako konstrukcyjnego elementu żelbetowego.
Poz.3.5.1. Zestawienie obciążeń obliczeniowych
Założono, że stopa fundamentowa obciążona jest jedynie pionową siłą osiową ze słupa, ponieważ mimośród niezamierzony w słupie jest wielkością pomijalnie małą, a obciążenia poziome przekazywane są na ściany zbiornika.
maksymalna obliczeniowa siła osiowa w poziomie dna zbiornika: N = 1331,3 kN
Sd
ciężar własny stopy:
⎡
−
2
h
w
⎤
G
= L ⋅ w +
⋅ L + L ⋅ a + a
⋅
⋅
=
des
⎢
( 2
2
25,0 1,1
,1
1
1 )
3
⎥
⎣
⎦
⎡
0,8 − 0,3
⎤
=
2
3,0 ⋅ 0,3 +
⋅
⎢
( 2
2
3,0 + 3,0 ⋅ 0,55 + 0,55 ) ⋅ 25,0⋅1,1 =
3
⎥
⎣
⎦
= 123,7 kN
Poz.3.5.2. Wymiarowanie stopy fundamentowej
Przyjęto:
Stal A-I (pręty φ16)
46
otulina: 50mm > c = 40mm (dla fundamentów posadowionych na min
podlewce z betonowej)
Oddziaływanie podłoża:
N
1331,3
Sd
q =
=
= 147,92 kPa < 150,0 kPa
r
2
B ⋅ L
3,0
zginanie stopy
Obliczenie zbrojenia na zginanie przeprowadzono metodą wydzielonych wsporników trapezowych.
( L − a )2 ⋅(2⋅ L + a ) (3,0 − 0,55)2 ⋅ 2⋅3,0 + 0,55
1
1
(
)
M = q ⋅
= 147,92 ⋅
r
24
24
= 242,32 kNm
d = 0,8 − 0,05 − 1,5 · 0,016 = 0,73 m 3
−
M
242,32 ⋅10
A =
=
= 0,001756 m2 = 17,56 cm2
s
f
⋅ 0,9 ⋅ d
210 ⋅ 0,9 ⋅ 0,73
yd
przyjęto zbrojenie 13φ14 A = 20,02 cm2
s
sprawdzenie stopy na przebicie
N
·
· ·
r’ – qr
A ≤ fctd up d
N
= 1331,3 kN
r’ = NSd
A = 1,952 = 3,80 m2
u = 0,5 · (4 · 1,950 + 4 · 0,45) = 4,80 m p
N
·
r’ – qr
A = 1331,3 – 147,92 · 3,80 = 769,2 kN
f · ·
ctd
up d = 1,33 · 103 · 4,80 · 0,73 = 4660,3 kN
N
·
· ·
r’ – q r
A = 769,2 kN < f
ctd
u p d = 4660,3 kN – warunek spełniony, przebicie stopy nie nastąpi 47