

Blok 9: Moment bezwładności. Moment siły.
Zasada zachowania momentu pędu
ZESTAW ZADAŃ NA ZAJĘCIA
Uwaga: w poniższych zadaniach przyjmij, że wartość przyspieszenia ziemskiego jest równa r
2
| g |= 10 m / s .
MOMENT BEZWŁADNOŚCI
1. Cztery kulki, każda o masie m = 5 g znajdują się w rogach kwadratu o boku a = 1 m . Oblicz moment bezwładności układu kulek względem osi zawierającej jeden z boków kwadratu oraz względem osi zawierającej przekątną kwadratu. Kulki traktujemy jak punkty materialne.
2. Oblicz moment bezwładności krążka o masie M i promieniu r względem osi prostopadłej do niego i stycznej do jego brzegu.
3. Oblicz moment bezwładności cienkiego jednorodnego pręta o długości L i masie m, względem osi prostopadłej do niego i przechodzącej przez:
• punkt odległy od środka pręta o L/4
• punkt leżący na końcu pręta
4. Układ składa się z dwóch jednorodnych kul o gęstości ρ i o promieniach równych odpowiednio r oraz R=3r. Odcinek łączący środki tych kul ma długość L=5r. Oblicz moment bezwładności układu względem osi prostopadłej do odcinka łączącego środki tych kul i przechodzącej przez środek masy większej kuli.
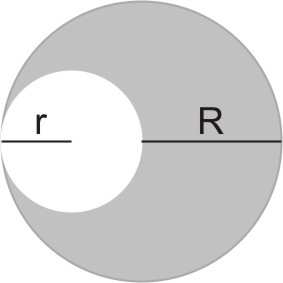
5. Z jednorodnej kuli o masie M i promieniu R wycięto kulę o promieniu R
r =
, której środek znajdował się w odległości r od środka dużej kuli.
2
Ile wynosi moment bezwładności wydrążonej kuli względem osi
przechodzącej przez punkt stanowiący środek masy pełnej dużej kuli i
stycznej do wydrążenia?
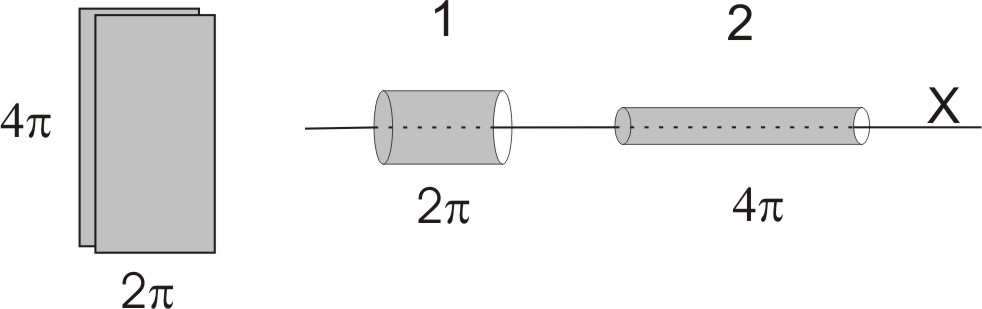
6. Z dwóch identycznych arkuszy
cienkiej blachy wykonano dwie rurki.
Oblicz stosunek momentów
bezwładności I / I tych rurek
1
2
względem ich osi X.
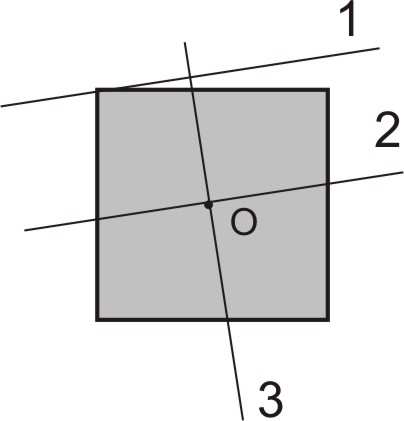
7. Zaznaczone na rysunku osie 1, 2, 3 leżą w płaszczyźnie
jednorodnego kwadratu o środku w punkcie O. Momenty
bezwładności kwadratu względem tych osi spełniają nierówność:
A)
I > I > I
1
2
3
B)
I < I < I
1
2
3
C)
I > I = I
1
2
3
D)
I < I = I
1
2
3
Projekt jest współfinansowany z Europejskiego Funduszu Społecznego
w ramach programu operacyjnego KAPITAŁ LUDZKI
1
BLOK 9 ZADANIA


MOMENT SIŁY
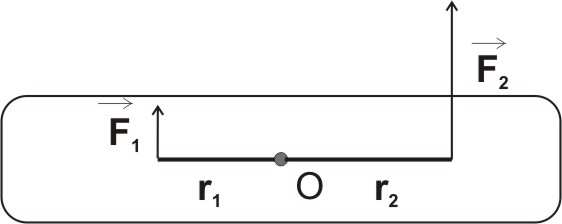
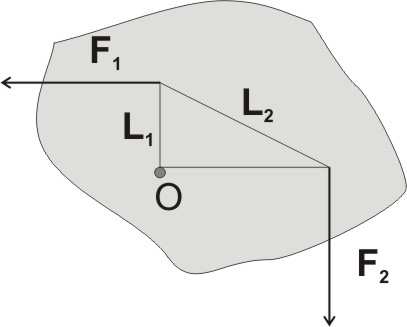
8. Stosunek wartości sił działających na bryłę
F
1
sztywną wynosi 1 =
. Jaki warunek spełniają
F
3
2
długości ramion tych sił, jeżeli wiadomo, że bryła
obraca się ruchem jednostajnym wokół osi O
prostopadłej do płaszczyzny rysunku?
9. W spoczywającej windzie na wadze dwuramiennej zawieszono dwie masy: m i 2m , które pozostawały w równowadze. Czy równowaga ta zostanie zaburzona (a jeśli tak, to w jaki sposób), jeżeli winda porusza się w górę ruchem jednostajnie przyspieszonym z przyspieszeniem o wartości a<g?
ZASADA ZACHOWANIA MOMENTU PĘDU
10. Średni okres wirowania gwiazdy wokół jej osi symetrii wynosi T = 30 dni ziemskich, a 1
gwiazda ma mas
30
10
ę M = 10
kg i promień R = 6 ⋅10 m . Oblicz do jakich rozmiarów powinna
się skurczyć ta gwiazda (bez zmiany masy), aby okres jej obrotu zmalał do T = 2 s .
2
Sprawdź, czy gwiazda ta byłaby wówczas stabilna, tzn. porównaj wartość przyspieszenia grawitacyjnego na równiku tej gwiazdy z wartością przyspieszenia dośrodkowego punktów równika.
11. Dwa krążki obracają się niezależnie w przeciwne strony z prędkościami kątowymi o wartościach: ω i ω na jednej osi przechodzącej przez ich środki i prostopadłej do ich 1
2
powierzchni. W pewnej chwili krążek górny spada na krążek dolny i krążki te „zlepiają się”.
Oblicz prędkość kątową złączonych krążków, jeżeli masa górnego krążka wynosi m , a jego 1
promień r , natomiast masa dolnego krążka wynosi m , a jego promień r . Oblicz zmianę 1
2
2
energii kinetycznej układu i wyjaśnij, dlaczego jest ona różna od zera (tzn. dlaczego nie obowiązuje zasada zachowania energii).
12. W środku poziomej tarczy o masie M = 200 kg i promieniu R = 2 m stoi człowiek o masie m = 50 kg . Tarcza obraca się z okresem T = 5 s . W pewnej chwili człowiek ten przeszedł na brzeg tarczy. Oblicz:
• okres ruchu tarczy po przejściu człowieka na jej brzeg
• o ile zmieni się energia kinetyczna układu
Zakładając, że człowiek przemieszcza się wzdłuż promienia tarczy ze stałą szybkością równą u = 5
,
0
m / s , wyprowadź równanie określające zależność prędkości kątowej tarczy od czasu.
Projekt jest współfinansowany z Europejskiego Funduszu Społecznego
w ramach programu operacyjnego KAPITAŁ LUDZKI
2
BLOK 9 ZADANIA


ZESTAW ZADAŃ DO SAMODZIELNEGO ROZWIĄZANIA
1. Na ciało działa para sił o jednakowych wartościach. Oblicz
wypadkowy moment siły działający na to ciało względem osi
prostopadłej do płaszczyzny rysunku i przechodzącej przez
punkt O. Kąty pomiędzy siłami i odpowiednimi ramionami sił są
kątami prostymi.
2. Jeżeli wypadkowy moment sił działających na ciało obracające
się wokół nieruchomej osi jest stały i różny od zera w czasie
ruchu, to moment pędu tego ciała:
A)
pozostaje stały
B)
na pewno jednostajnie wzrasta z czasem
C)
na pewno jednostajnie maleje z czasem
D)
jednostajnie wzrasta lub maleje z czasem
3. Oblicz moment bezwładności cienkościennego rurki o masie M i promieniu R względem osi równoległej do jej wysokości i stycznej do jej pobocznicy.
4. Człowiek siedzący na krześle obrotowym obraca się z prędkością kątową o wartości ω (tarcie pomijamy). W wyciągniętych na boki rękach trzyma dwa jednakowe ciężarki. Jeśli człowiek opuści ręce, to:
A)
moment pędu i energia kinetyczna układu wzrosną
B)
moment pędu i energia kinetyczna układu zmaleją
C)
ani energia kinetyczna, ani moment pędu układu nie ulegną zmianie
D)
moment pędu układu pozostanie niezmieniony, a energia kinetyczna układu wzrośnie 5. Jeżeli bryła sztywna wiruje wokół stałej osi i względem tej osi ma moment bezwładności I, a względem punktu leżącego na tej osi - moment pędu o wartości L, to okres obrotu bryły względem tej osi jest równy:
I
A)
2 L
π
2 L
π
B)
I
2 I
π
C)
L
D) 2 I
π L
Projekt jest współfinansowany z Europejskiego Funduszu Społecznego
w ramach programu operacyjnego KAPITAŁ LUDZKI
3
BLOK 9 ZADANIA


