Blok 4: Dynamika ruchu postępowego.

Równia, wielokrążki, układy ciał.

ZESTAW ZADAŃ NA ZAJĘCIA

Uwaga: w poniższych zadaniach przyjmij, że wartość przyspieszenia ziemskiego jest równa r

2

| g |= 10 m / s .

UKŁADY CIAŁ

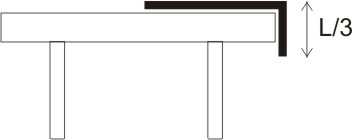
1. Jednorodna linka o długości L w sytuacji przedstawionej na rysunku zaczyna się zsuwać ze stołu, gdy 1/3 jej

długości zwisa. Oblicz współczynnik tarcia statycznego linki o stół.

2. Ruch zsuwającej się ze stołu linki ( w zad. 1) jest ruchem:

A) niejednostajnie przyspieszonym

B) jednostajnie przyspieszonym, z przyspieszeniem o wartości a = g C) jednostajnie przyspieszonym, z przyspieszeniem o wartości a < g D) jednostajnym

r

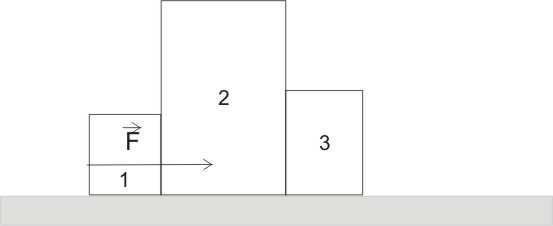
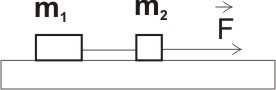
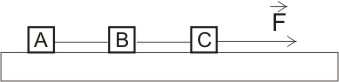
3. Układ trzech stykających się z sobą klocków pchamy siłą F o wartości F = 10 N , jak pokazano na rysunku. Zakładamy, że klocki poruszają się po poziomym podłożu bez tarcia. Masy klocków: m = 1 kg, m = 4 kg, m = 2 kg

1

2

3

. Oblicz

wartości:

• przyspieszenia układu klocków

• sił wypadkowych działających na

każdy klocek

• siły 1

F 2 , którą klocek 1 działa na

klocek 2

• siły 3

F 2 , którą klocek 3 działa na

klocek 2

4. Dwie jednakowe skrzynie ruszają z miejsca pod wpływem działania sił, jak pokazuje rysunek.

Czasy t1 i t 2 , po których dojadą do krawędzi stołów przebywając jednakowe drogi spełniają zależność (tarcie

pomijamy):

A) t =

1

t 2

B) t >

2

t1

C) t <

2

t1

D) t >

, je

t =

, gdy masa ka

2

t1

śli masa każdej skrzyni jest mniejsza niż 5,5 kg, 1

t 2

żdej

skrzyni jest równa 5,5 kg oraz t <

, je

2

t1

śli masa każdej skrzyni jest większa niż 5,5 kg

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego w ramach programu operacyjnego KAPITAŁ LUDZKI

1

BLOK 4

WIELOKRĄŻKI

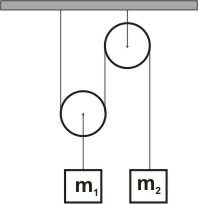
5. Ciężarki o masach m = 2 kg

=

1

i m

3 kg,

2

połączono nicią. Nić

przerzucono przez bloczek. Pomijając masę bloczka, oblicz:

•

przyspieszenie ciężarków

•

siłę napięcia nici

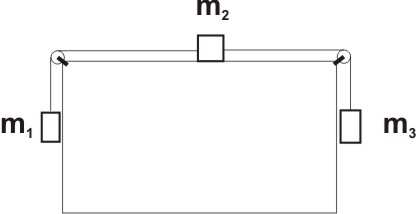
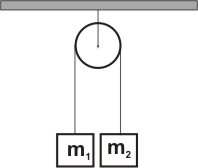
6. Układ przedstawiony na rysunku (masy bloczków i liny pomijamy) pozostaje w równowadze, gdy:

A) m =

1

m 2

B) m =

2

2m1

C)

1

m =

1

2

m1

D) m =

2

2

m1

3

7. Oblicz wartość przyspieszenia układu klocków

przedstawionego na rysunku (pomijamy opory).

Przyjmij, że m = k

3 g,

=

=

1

m

k

3 g,

2

m

4kg

3

. W

którą stronę poruszają się klocki?

8. Siła wypadkowa działająca na klocek m1

( w poprzednim zadaniu):

A) ma taką samą wartość, jak siła wypadkowa

działająca na klocek o masie m 2

B) jest mniejsza od siły wypadkowej działającej na klocek o masie m 2

C) jest większa od siły wypadkowej działającej na klocek o masie m 2

D) jest większa od siły wypadkowej działającej na klocek o masie m3

RÓWNIA

9. Jeżeli umieszczony na równi pochyłej klocek pozostaje w spoczynku, to: A) Siła tarcia równoważy siłę ciężkości działającą na klocek B) Siła tarcia jest większa niż składowa siły ciężkości równoległa do równi C) Równoważą się siły: ciężkości klocka, tarcia działająca na klocek i nacisku klocka na równię D) Równoważą się: siły ciężkości klocka, sprężystości równi i tarcia działająca na klocek 10. Na równi pochyłej leży klocek. Klocek zaczyna się zsuwać z równi przy kącie nachylenia równym 30o. Oblicz współczynnik tarcia. Który współczynnik możesz obliczyć w tym zadaniu: tarcia statycznego czy kinetycznego?

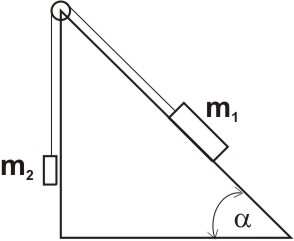
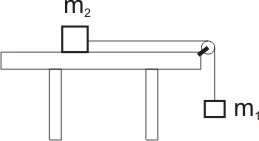
11. W sytuacji przedstawionej na rysunku klocek o masie m 2

będzie się poruszał z przyspieszeniem zwróconym w górę, gdy zostanie spełniony warunek (tarcie pomijamy):

m

A)

1 > sin α

B) m >

1

m 2

m 2

m

m

C)

2 < sin α

D)

2 < tgα

m1

m1

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego w ramach programu operacyjnego KAPITAŁ LUDZKI

2

BLOK 4

12. Rozpędzony do szybkości

m

v =

0

10

narciarz wjeżdża w wskutek rozpędu na zbocze. Kąt

s

nachylenia zbocza do poziomu wynosi

o

α = 30 . Współczynniki tarcia statycznego i

kinetycznego między śniegiem a nartami wynoszą odpowiednio: µ = , 0 2

µ =

s

i

1

,

0

k

.

•

Oblicz drogę przebytą przez narciarza aż do zatrzymania.

•

Oblicz czas jego wjeżdżania na zbocze.

•

Zbadaj, czy narciarz po zatrzymaniu zacznie zjeżdżać z powrotem w dół.

ZESTAW ZADAŃ DO SAMODZIELNEGO ROZWIĄZANIA

1. Jeśli w sytuacji przedstawionej na rysunku (tarcie pomijamy) masy ciał są równe odpowiednio: m = 4 kg

=

1

, m

k

1 g

2

, to siła napinająca nitkę łączącą

klocki ma wartość:

A) 1 F

B) 1 F

C) 3 F

D) 4 F

4

3

4

5

2. Trzy klocki o jednakowych masach m są połączone nitkami. Klocek jest ciągnięty w prawo siłą o wartości F nadającą całemu układowi przyspieszenie. Jeżeli założymy, że nie ma tarcia między klockami i podłożem, to wypadkowa siła działająca na klocek B wynosi: A) zero

B) 1 F C) 1 F

D) F

3

2

3. Przyspieszenie klocków przedstawionych na rysunku ma wartość

2

a = 3 m / s . Pomijamy masę nitki i bloczka. Masa

m = 3 kg

=

1

, a m

2kg

2

.Oblicz współczynnik tarcia

kinetycznego klocka o stół oraz wartość napięcia nici.

4. Gdyby pominąć tarcie, to w poprzednim zadaniu:

A) układ klocków poruszałby się z przyspieszeniem ziemskim B) siła napięcia nici byłaby równa zeru

C) siła napięcia nici byłaby równa ciężarowi klocka o masie m1

D) wartość siły wypadkowej działającej na klocek o masie m 2 byłaby równa wartości siły naciągu nici

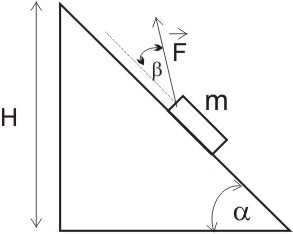
5. U podstawy równi o kącie nachylenia

o

α = 30 i wysokości równi H = 2 m znajduje się klocek o masie m = 1 kg , do którego przyłożono siłę F = 10 N pod kątem o

β = 30 względem

powierzchni zbocza równi. Pomijając tarcie, oblicz:

• przyspieszenie klocka

• czas, po którym klocek osiągnie szczyt równi

• szybkość końcową (przy wierzchołku równi)

• siłę nacisku klocka na równię

Projekt jest współfinansowany z Europejskiego Funduszu Społecznego w ramach programu operacyjnego KAPITAŁ LUDZKI

3

BLOK 4